文档内容
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上大题无效。满分150分。考试时间120
分钟。考试结束后,将本试题卷和答题卡上一并交回。
第Ⅰ卷 (选择题 共 50 分)
注意事项:
必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。
一、选择题:本大题共 10 小题,每小题 5 分,共 50 分。在每小题给出的四个选项中,
只有一个是符合题目要求的。
1、设集合A={1,2,3},集合B={-2,2},则A B=( )
I
(A)Æ (B){2}
(C){-2,2} (D){-2,1,2,3}
2、一个几何体的三视图如图所示,则该几何体可以是( )
(A)棱柱 (B)棱台
(C)圆柱 (D)圆台
3、如图,在复平面内,点A表示复数z,则图中表示z的共轭复数的点是( ) x
A
C
(A)A (B)B
(C)C (D)D O y
B
D
4、设xÎZ ,集合A是奇数集,集合B是偶数集.若命题 p:"xÎA,2xÎB,则( )
(A)Øp:$xÎA,2xÎB (B)Øp:$xÏA,2xÎB
(C)Øp:$xÎA,2xÏB (D)Øp:"xÏA,2xÏB
5、抛物线y2 =8x的焦点到直线x- 3y =0的距离是( )
(A)2 3 (B)2
第1页 | 共6页(C) 3 (D)1
p p
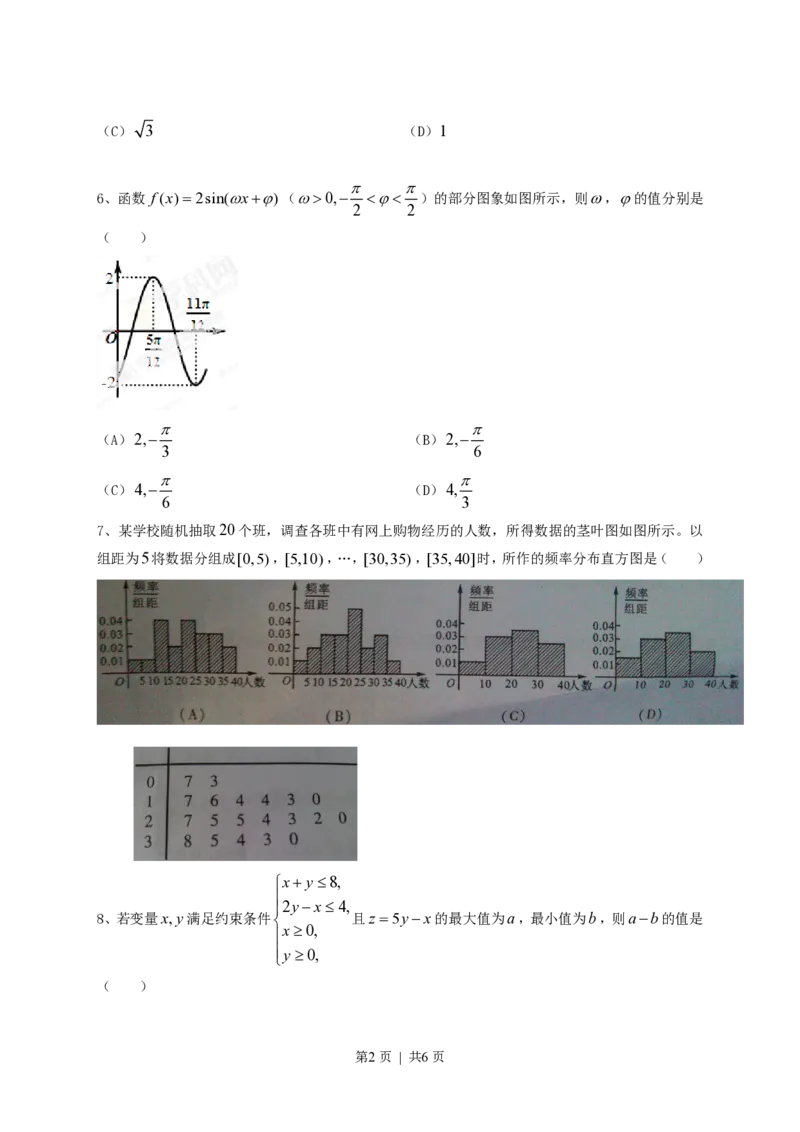
6、函数 f(x)=2sin(wx+j)(w>0,- b>0)上一点P向x轴作垂线,垂足恰为左焦点F ,A是椭圆与x轴正
a2 b2 1
半轴的交点,B是椭圆与 y轴正半轴的交点,且AB//OP(O是坐标原点),则该椭圆的离心率是
( )
2 1 2 3
(A) (B) (C) (D)
4 2 2 2
10、设函数 f(x)= ex +x-a (aÎR,e为自然对数的底数)。若存在bÎ[0,1]使 f(f(b))=b
成立,则a的取值范围是( )
(A)[1,e] (B)[1,1+e] (C)[e,1+e] (D)[0,1]
第二部分 (非选择题 共 100 分)
注意事项:
必须使用0.5毫米黑色签字笔在答题卡上题目所指示的答题区域内作答。作图题可先用铅笔绘
出,确认后再用0.5毫米黑色墨迹签字笔描清楚。答在试题卷上无效。
二、填空题:本大题共 5 小题,每小题 5 分,共 25 分。
11、lg 5+lg 20 的值是____________.
uuur uuur uuur
12、如图,在平行四边形 ABCD中,对角线 AC与 BD交于点 O, AB+ AD=lAO,则
l=____________.
a
13、已知函数 f(x)=4x+ (x>0,a >0)在x=3时取得最小值,则a=____________.
x
p
14、设sin2a=-sina,aÎ( ,p),则tan2a的值是____________.
2
15、在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),D(7,-1)的距离之和最小的点的坐标
是_______.
三、解答题:本大题共 6 小题,共 75 分。解答应写出文字说明,证明过程或演算步骤。
16、(本小题满分12分)
第3页 | 共6页在等比数列{a }中,a -a =2,且2a 为3a 和a 的等差中项,求数列{a }的首项、公比及前n
n 2 1 2 1 3 n
项和.
17、(本小题满分12分)
在 DABC中 , 角 A,B,C的 对 边 分 别 为 a,b,c, 且
3
cos(A-B)cosB-sin(A-B)sin(A+C)=- .
5
(Ⅰ)求sinA的值;
uuur uuur
(Ⅱ)若a=4 2,b=5,求向量BA在BC方向上的投影.
18、(本小题满分12分)
某算法的程序框图如图所示,其中输入的变量x在1,2,3,×××,24这24个整数中等可能随机产生。
(Ⅰ)分别求出按程序框图正确编程运行时输出 y的值为i的概率P(i =1,2,3);
i
(Ⅱ)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出 y
的值为i(i =1,2,3)的频数。以下是甲、乙所作频数统计表的部分数据。
甲的频数统计表(部分) 乙的频数统计表(部分)
运行 输出 y的值 输出 y的值 输出 y的值
次数n 为1的频数 为2的频数 为3的频数
30 14 6 10
… … … …
2100 1027 376 697
第4页 | 共6页运行 输出 y的值 输出 y的值 输出 y的值
次数n 为1的频数 为2的频数 为3的频数
30 12 11 7
… … … …
当n=2100时,根据表中的数据,分别写 2100 1051 696 353
出甲、乙所编程序各自输出 y的值为i(i =1,2,3)的频率(用分数表示),并判断两位同学中哪一位
所编写程序符合算法要求的可能性较大。
19、(本小题满分12分)
如 图 , 在 三 棱 柱 ABC-ABC 中 , 侧 棱 AA ^底 面 ABC, AB= AC =2AA =2,
1 1 1 1
ÐBAC =120o,D,D 分别是线段BC,BC 的中点,P是线段AD上异于端点的点。
1 1 1
(Ⅰ)在平面ABC内,试作出过点P与平面ABC平行的直线l,说明理由,并证明直线l ^
1
平面ADD A ;
1 1
(Ⅱ)设(Ⅰ)中的直线l交 AC于点Q,求三棱锥 A -QC D的体积.(锥体体积公式:
1 1
1
V = Sh,其中S 为底面面积,h为高)
3
20、(本小题满分13分)
已知圆C的方程为x2 +(y-4)2 =4,点O是坐标原点.直线l: y =kx与圆C交于M 、N 两
点.
(Ⅰ)求k的取值范围;
2 1 1
(Ⅱ)设Q(m,n)是线段MN 上的点,且 = + .请将n表示为m的函数.
|OQ|2 |OM |2 |ON |2
21、(本小题满分14分)
ìx2 +2x+a,x<0
已知函数 f(x)=í ,其中a是实数。设 A(x , f(x )),B(x , f(x ))为该函
îlnx,x>0 1 1 2 2
数图象上的两点,且x < x 。
1 2
(Ⅰ)指出函数 f(x)的单调区间;
(Ⅱ)若函数 f(x)的图象在点A,B处的切线互相垂直,且x <0,证明:x -x ³1;
2 2 1
第5页 | 共6页(Ⅲ)若函数 f(x)的图象在点A,B处的切线重合,求a的取值范围。
第6页 | 共6页