文档内容
一、选择题:本大题共 9 小题,每小题 5 分,共 45 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.复数z=i·(1+i)(i为虚数单位)在复平面上对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.“1<x<2”是“x<2”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件。为了解它们的
产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间
的产品中抽取了3件,则n=( )
A.9 B.10 C.12 D.13
4.已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)
等于( )
A.4 B.3 C.2 D.1
5.在锐角ABC中,角A,B所对的边长分别为a,b. 若2asinB= 3b,则角A等于( )
A. B. C. D.
3 4 6 12
6.函数f(x)=㏑x的图像与函数g(x)=x2-4x+4的图像的交点个数为( )
A.0 B.1 C.2 D.3
7.已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为 2 的矩形,则
该正方体的正视图的面积等于( )
3 2+1
A. B.1 C. D. 2
2 2
8.已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的最大值为( )
A. 2-1 B. 2 C. 2+1 D. 2+2
第1页 | 共5页1
9.已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为 ,
2
AD
则 =( )
AB
1 1 3 7
A. B. C. D.
2 4 2 4
二、填空题:本大题共 6 小题,每小题 5 分,共 30 分。
10.已知集合U ={2,3,6,8},A={2,3},B={2,6,8},则(CÈA)ÇB=________
ìx=2s+1, ìx=at,
11.在平面直角坐标系xOy中,若直线l :í (s为参数)和直线l :í (t为参数)
1 îy =s 2 îy =2t-1
平行,则常数a的值为________
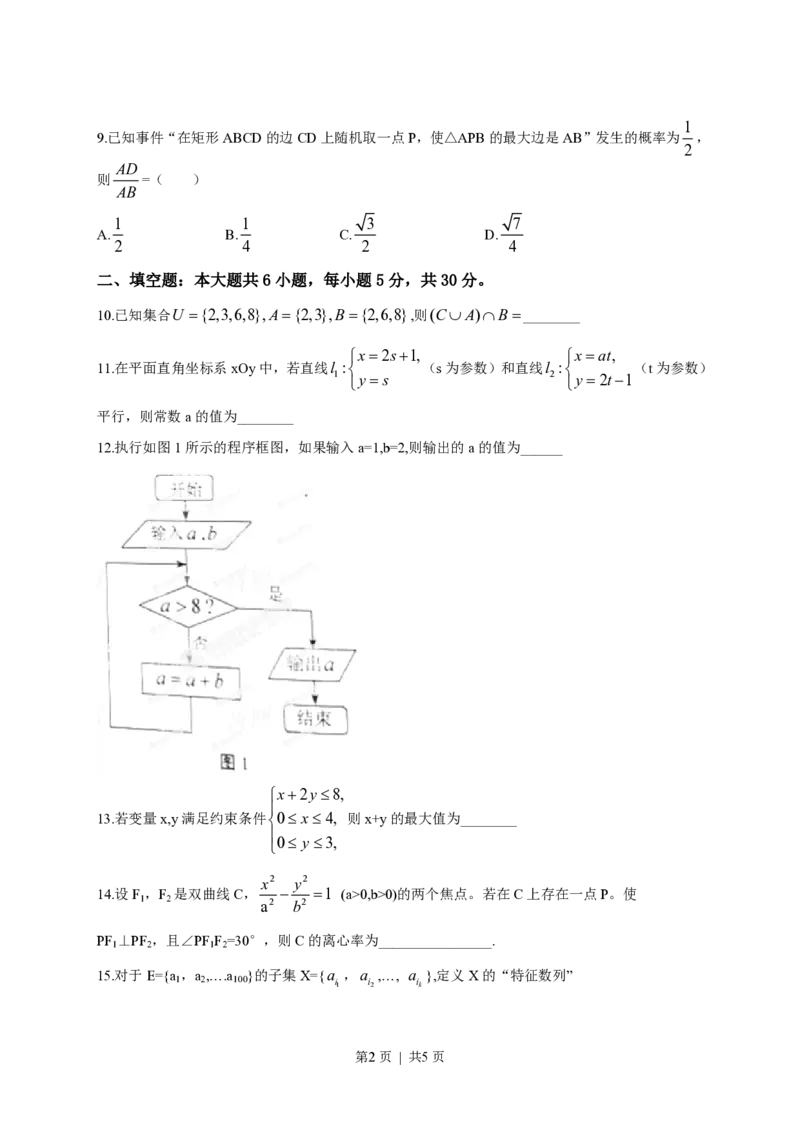
12.执行如图1所示的程序框图,如果输入a=1,b=2,则输出的a的值为______
ìx+2y£8,
ï
13.若变量x,y满足约束条件í0£ x£4, 则x+y的最大值为________
ï
0£ y£3,
î
x2 y2
14.设F ,F 是双曲线C, - =1 (a>0,b>0)的两个焦点。若在C上存在一点P。使
1 2 a2 b2
PF ⊥PF ,且∠PF F =30°,则C的离心率为________________.
1 2 1 2
15.对于E={a ,a ,….a }的子集X={a ,a ,…, a },定义X的“特征数列”
1 2 100 i i i
1 2 k
第2页 | 共5页为x ,x …,x ,其中x =x =…=x =1.其余项均为0,例如子集{a ,a }的
1 2 100 i i i 2 3
1 2 k
“特征数列”为0,1,0,0,…,0
(1) 子集{a ,a a }的“特征数列”的前三项和等于________________;
1 3, 5
(2) 若E的子集P的“特征数列”P ,P ,…,P 满足P +P =1, 1≤i≤99;
1 2 100 1 i+1
E 的子集Q的“特征数列” q ,q ,…,q 满足q =1,q +q +q =1,
1 2 100 1 1 j+1 j+2
1≤j≤98,则P∩Q的元素个数为___________.
三、解答题;本大题共 6 小题,共 75 分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
已知函数
2
(1) 求 f( )的值;
3
1
(2) 求使 f(x)< 成立的x的取值集合
4
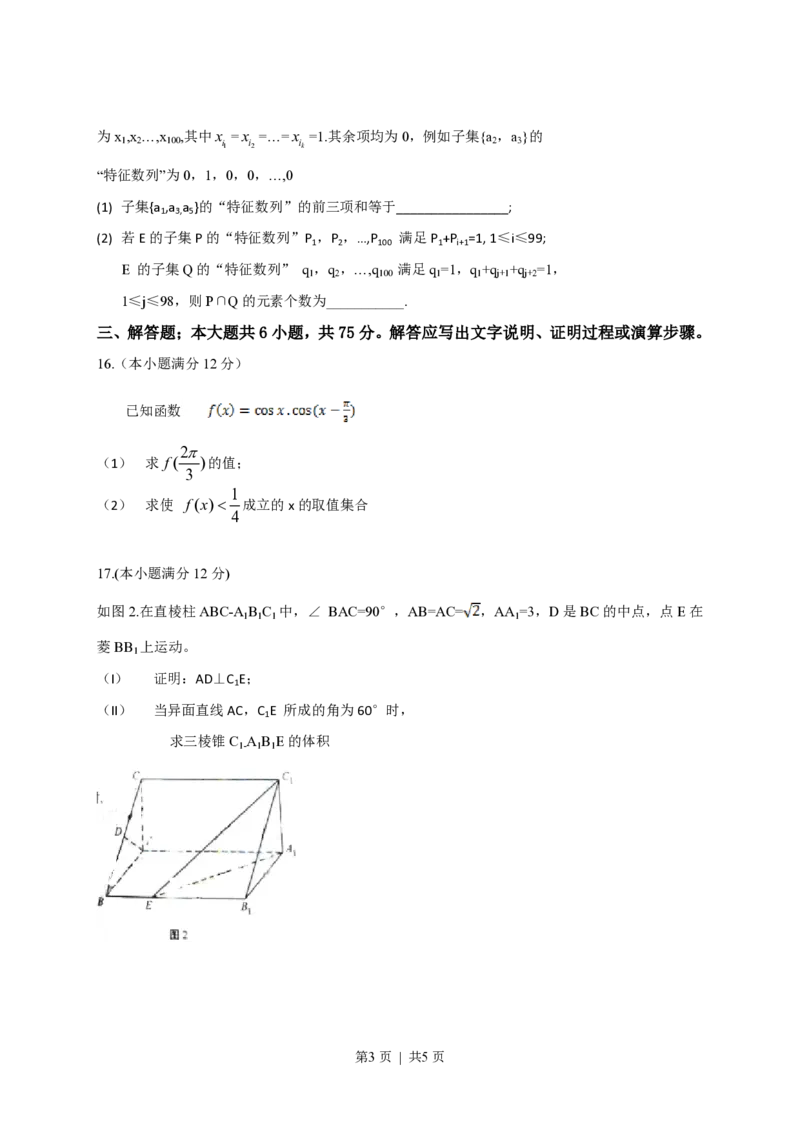
17.(本小题满分12分)
如图2.在直棱柱ABC-A B C 中,∠ BAC=90°,AB=AC= ,AA =3,D是BC的中点,点E在
1 1 1 1
菱BB 上运动。
1
(I) 证明:AD⊥C E;
1
(II) 当异面直线AC,C E 所成的角为60°时,
1
求三棱锥C A B E的体积
1- 1 1
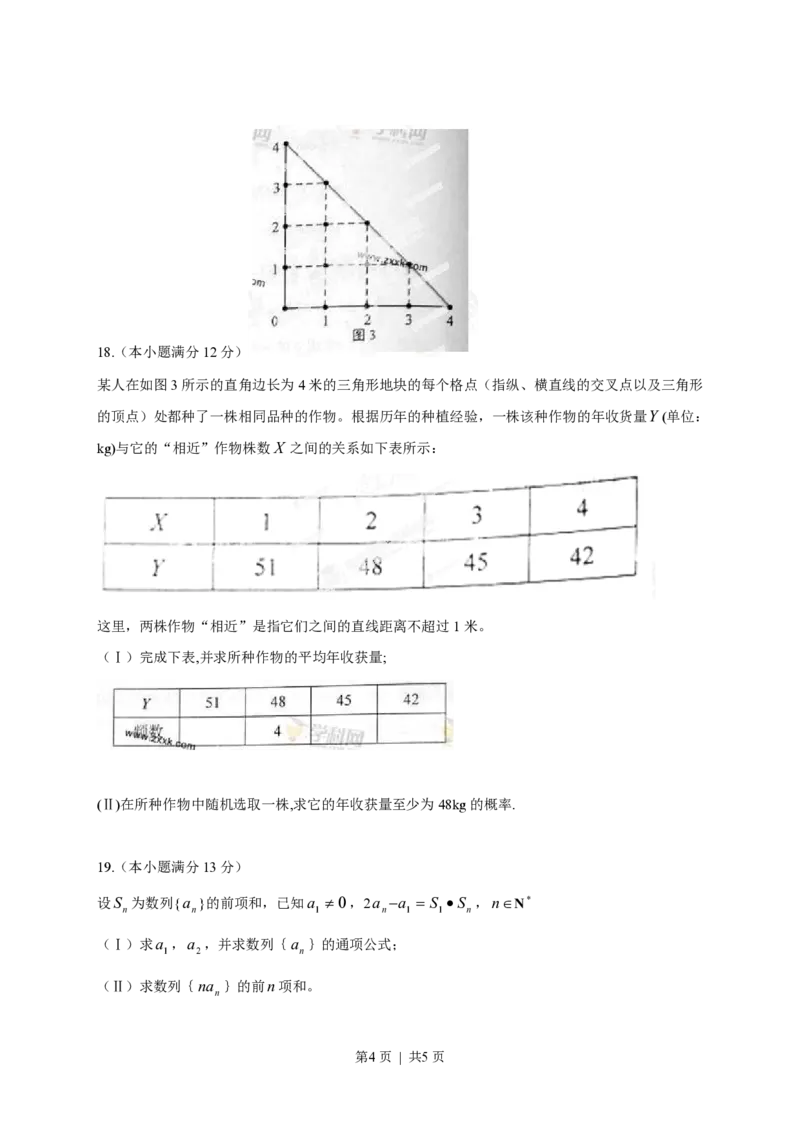
第3页 | 共5页18.(本小题满分12分)
某人在如图3所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形
的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收货量Y (单位:
kg)与它的“相近”作物株数X 之间的关系如下表所示:
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(Ⅰ)完成下表,并求所种作物的平均年收获量;
(Ⅱ)在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.
19.(本小题满分13分)
设S 为数列{a }的前项和,已知a 0,2a -a = S S ,nN
n n 1 n 1 1 n
(Ⅰ)求a ,a ,并求数列{a }的通项公式;
1 2 n
(Ⅱ)求数列{na }的前n项和。
n
第4页 | 共5页20.(本小题满分13分)
x2
已知F ,F 分别是椭圆E: + y2 =1的左、右焦点F ,F 关于直线x+ y-2=0的对称点是
1 2 5 1 2
圆C的一条直径的两个端点。
(Ⅰ)求圆C的方程;
(Ⅱ)设过点F 的直线l被椭圆E和圆C所截得的弦长分别为a,b。当ab最大时,求直线l的方
2
程。
21.(本小题满分13分)
1-x
已知函数f(x)= ex.
1+ x2
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明:当f(x )=f(x )(x ≠x )时,x +x <0.
1 2 1 2 1 2
第5页 | 共5页