202309高三入学摸底考试答案（数学）(1)_2023年9月_029月合集_2024届新时代NT教育高三入学摸底考试

新时代 NT 教育 2023-2024 学年高三入学摸底考试 数学 参考答案 （新高考） 1.D【解析】当A时，a=0, 当A2 时，a1, 当A 2 时，a=1,a1,0,1  . 2 2.B【解析】z 1i,zi. 1i 3.B【解析】当（k2)(k2)0,即 k 2或k 2时， x2  y2 1 表示双曲线， k2 k2 所以“k 2”是“ x2  y2 1 表示双曲线”的充分不必要条件. k2 k2 4.D【解析】由题分析得 a  1  1  1 , n n(n1) n n1 所以 1 1 1 1 1 10 a a a a 1      . 1 2 3 10 2 2 3 10 11 11   2   2     5.A【解析】 ab  ab 4ab523，ab  3. 6.C【解析】 tan( 5 )tan（  ) 1tan 2，tan3， 4 4 1tan 1tan2 4 cos2cos2sin2  . 1tan2 5 7.A【解析】当n1时，a T 1,当n2时，a  T n  n 1 1 ，a a a a 1, 1 1 n T n1 n1 2 3 4 n n1 而a 1，a为最小项，a 为最大项. 1 1 2 8.D【解析】由已知得函数 f(x) 既关于原点对称，又关于 x1 对称，所以周期 T = 4， 设g(x)log x2，而g(3)g(7)1 ，由函数图像可分析 f(x)与g(x)的交点个数为5. 5 1 1 2 9.AB【解析】若a0,b0,则ab 2 ab 2 2 ，当且仅当 ab 时取等号. ab ab 2 ∴A正确； f(x) x3是在R上单调递增的函数，若f(a)  f(b)，则a b，∴B正确； 若a0, f(x) xa在（0，）单调递减， ( 2 )a ( 3 )a，∴C错误； 5 5 1 1 若  0,则0ab,lnalnb，∴D错误. a b 10.BC【解析】x 2 ( x 1  x 2  x n)2  x 1 2  x 2 2  x n 2 ,∴A错误; n n 数学 第 1 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}由s2  1  10 x2x 2 , 10 x2 10（s2x 2 )130，∴B正确; 10 i i i1 i1 由~B（9， 1 ）得，D()2，D(2)4D()8,∴C正确; 3 数据2，3，4，7，8，10，17，18的第50百分位数是7.5，∴D错误 11.ACD【解析】取BD的中点N,BA的中点F,连结MN,NF,EF,则四边形EMNF 为平行四边形,MN //EF,MN 面BAE,MN //面BAE ,∴A正确; 假设存在一个位置使得 BD  AE ，取 AE 中点 H，连结 BH,DH ,显然 BH  AE,BH BDB,AE 面BHD，AE  DH ,进而有DA=DE, 而由题可得DE  3  DA,∴不存在BD  AE ，故B错误; 当BD  EC 时，则 BD AD，而DE  AD,AD面BDE,面BDE 面ADE, 且面BDE面ADE DE,B到面ADE的距离即B到DE的距离d， 在BDE中，BE 2,BD  DE  3, 由S  2  1  3d,d  2 6 ,∴C正确; BDE 2 3 当面BAE 面ABCD时，四棱锥BAECD的体积最大，此时棱锥的高为 3， 1 V  1 3 3 1.∴D正确. BAECD 3 12. ACD【解析】设切点(m,lnm1)， k  f(m) 1 ,lnm1 1 m,lnm2,me2， m m x 所以过原点的切线方程为 y  ，∴A正确； e2 与 f(x)关于 y  x对称的函数为 y ex1,∴B错误； 若过点(a,b)有2条直线与 f(x)相切，则点(a,b)在f(x)上方，即b f(a),即blna1,∴C正确; 由于xR,lnx x1，lnx1 x2 ，∴D正确. 5  13. 【解析】 y x2为偶函数，所以g(x)cos(2x )，（0，）为奇函数， 6 3   5   k,kZ, . 3 2 6 h 14. 13 2【解析】易得棱台的高 h 2，V  (S  S S S ）13 2 . 棱台 上 上 下 下 3 3 3 15.11【解析】 a1,b0,2ab2(a1）b2[2(a1)b]( 2  1 )27 （2 a1)  2b 11 , a1 b b a1 b2 (a1)2时取等号. 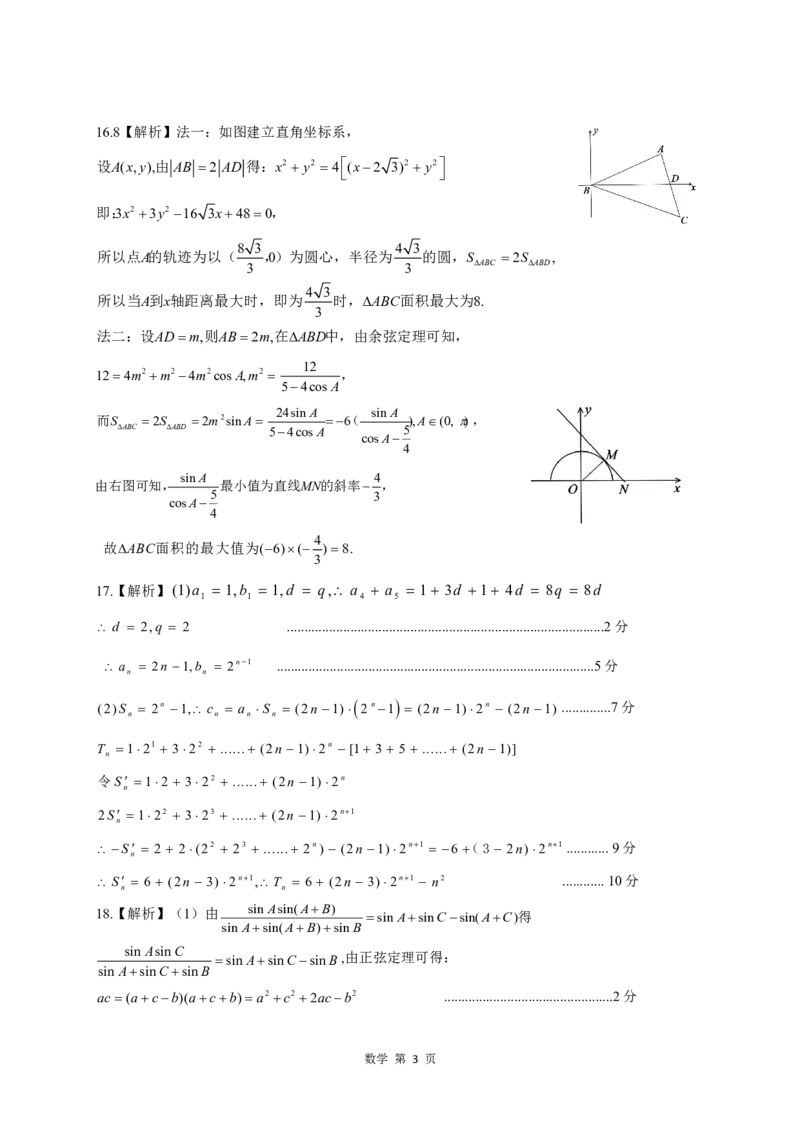数学 第 2 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}16.8【解析】法一：如图建立直角坐标系， 设A(x,y),由 AB 2 AD 得：x2  y2 4(x2 3)2  y2   即：3x2 3y2 16 3x480， 8 3 4 3 所以点A的轨迹为以（ ，0）为圆心，半径为 的圆，S 2S , 3 3 ABC ABD 4 3 所以当A到x轴距离最大时，即为 时，ABC面积最大为8. 3 法二：设ADm,则AB2m,在ABD中，由余弦定理可知， 12 124m2m24m2cosA,m2  ， 54cosA 24sinA sinA 而S 2S 2m2sinA 6（ ),A(0, ) ， ABC ABD 54cosA 5 cosA 4 sinA 4 由右图可知， 最小值为直线MN的斜率 ， 5 3 cosA 4 4 故ABC面积的最大值为(6)( )8. 3 17.【解析】(1)a  1,b  1,d  q, a  a  1 3d 1 4d  8q  8d 1 1 4 5  d  2,q  2 ..........................................................................................2分  a  2n 1,b  2n1 ..........................................................................................5分 n n (2)S  2n 1,c  a S  (2n 1)  2n1   (2n 1)2n  (2n 1) ..............7分 n n n n T 121  322  ...... (2n 1)2n [1 3  5  ...... (2n 1)] n 令S 12  322  ...... (2n 1)2n n 2S 122  323  ...... (2n 1)2n1 n  S  2  2(22  23  ...... 2n)  (2n 1)2n1  6 （3  2n)2n1............9分 n  S  6  (2n  3)2n1,T  6  (2n  3)2n1  n2 ............10分 n n 18.【解析】（1）由 sin Asin(AB) sin AsinCsin(AC)得 sin Asin(AB)sinB sin AsinC sin AsinCsinB,由正弦定理可得： sin AsinCsinB ac(acb)(acb)a2 c2 2acb2 ................................................2分 数学 第 3 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}即a2 c2 b2 ac,cosB  a2 c2 b2  1 ,B(0,)B  2 .............................4分 2ac 2 3   (2)S  1 acsinB 3 ac 3,ac4，由  B  D   BABC ，4  B  D  2 (  B  A    B  C  )2 .....8分 ABC 2 4 2 24 a2 c2 2accosB  a2 c2 4，a2 c2  28................................................10分 b2  a2 c2 2accosB  28432b  4 2..........................................................12分 1 19.【解析】（1）当 a 1时，设 h(x)  f (x) g(x)1 ex ln(x1)1,h(x)  ex  ， x1 1 ex  只有一个解x0,x0时h(x)0,1 x0时，h(x)0 x1 h(x)在(1，0)单调递减，(0，)单调递增，....................................................................2分 h(x)h(0),而h(0)0,h(x)0,即f(x) g(x)1.......................................................4分 （2）法一：若x（1，），f(x)g(x)1恒成立， x1 即：aex ln 1aex lnalnx11 a 即aex  ln aex  x 1 ln(x 1) ................................................................................6分 构造函数m(t)  t  ln t,易知m(t)在(0， )递增， 则不等式为m(aex)  m(x 1) .....................................................................................8分 x 1 x 1  aex  x 1 a  ,设(x)  (x  1) ex ex (x)  x (x  1),则(x)在（ 1，0)递增，0， 递减，..................................10分 ex (x) (0) 1, a  1............................................................................................12分 max 法二：x（1，），f(x)g(x)1恒成立，即 aex lnaln（x1）1 0； 令F（x)  aex ln(x 1) lna 1 F(x)aex  1 （, a0）,aex  1 有唯一实数根，设为x，(x 1)................................6分 x1 x1 0 0 1 即aex0  ,lnax ln(x 1), 则F（x)在(1,x )递减，在(x，)递增， x 1 0 0 0 0 0 F(x) F(x )aex0 ln(x 1）lna10.....................................................................8分 min 0 0 即： 1 x 2ln(x 1)10 , x 1 0 0 0 1 设h(x) x2ln(x1)1,显然h(x)在(1，)单调递减， x1 数学 第 4 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}而（h 0）0，h(x )0,则1 x 0,...................................................................................10分 0 0 lnaln(x 1)x ,x (1,0], lna0, a1. ........................................................12分 0 0 0 20.【解析】(1)取SC 中点F ，连接EF,FD，E,F分别为SB,SC的中点， 1 EF //BC，EF  BC， 2 底面四边形ABCD是矩形， P 为棱AD的中点， 1 PD//BC，PD BC．EF//PD，EF PD， 2 故四边形PEFD是平行四边形，\PE//FD...................................................................2分 又FD平面SCD，PE平面SCD，∴PE//平面SCD...........................................4分   (2)以点P为原点，PA，PS的方向分别为x,z轴的正方向，建立如图所示的空间直角坐标系， 设AD=2,则P0,0,0，A1,0,0，B1,1,0，S  0,0, 3  ............................................6分     2 3   n PB  0 若SM  2MA,M（ ，0， ）设面PMB的法向量为n , 1  3 3 1 n PM  0 1   取n ( 3, 3,2),取面SAD的法向量n (0,1,0).....................9分 1 2   cos n  ,n   n 1   n 2   30 .....................................................11分 1 2 n n 10 1 2 面SAD和面PMB夹角的余弦值为 30 ...............................12分 10 1 2 1 2 1 21.【解析】 （1）同学甲在游戏终止时成功通过两个关卡的概率P=     ............4分 2 3 2 3 9 （2）同学甲成功通过关卡的个数ξ的值为0，1，2 .......................................................................6分 1 1 1 1 1 1 1 1 11 1 2 1 1 2 1 1 5 P(ξ=0)=         P(ξ=1)=       2 2 2 3 2 2 3 2 3 18 2 3 2 2 3 2 3 18 P(ξ=2)= 1  2  1  2  1 ......................................................................11分 2 3 2 3 9 所以同学甲成功通过关卡的个数ξ的分布列为： ξ 0 1 2 11 5 1 .......................................................................12分 P 18 18 9 数学 第 5 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}4 1  1  22.【解析】由题可得  a2 b2 所求椭圆方程为： x2  y2 1 .......................4分 c 2 a2 6 6 3    a 2 b2 3 a2 b2c2   （2)方法一：设过点A的直线为y 1 k(x  2)与y  tx2(t  0)相切， y 1 k(x  2)   tx2  kx  2k 1 0    k2  4t(2k 1） 0， y  tx2 k  k  8t k  k 1 1 ..............6分  1 2  1 2    2,(k，k 分别是直线PA和QA的斜率） k k  4t k k k k 1 2 1 2 1 2 1 2 设直线PQ为：ymxn，P(x,y),Q(x ,y ), 1 1 2 2 ymxn  得:(12m2)x2 4mnx2n2 60, x2 2y2 6 4mn 2n2 6 则x  x  ,x x  ， 1 2 12m2 1 2 12m2 由 0得：6m2n230 ..........................................................................8分 1 1 x 2 x 2 x 2 x 2   1  2  1  2 2 ， k k y 1 y 1 mx n1 mx n1 1 2 1 2 1 2 即（x 2)(mx n1)(x 2)(mx n1) 2(mx n1)(mx n1)得： 1 2 2 1 2 1 （2m2m2)x x (n12mn)(x x )2(n2 1)0, 1 2 1 2 （2m2m2（) n23)(n12mn)(2mn)(n21)(12m2)0, 整理得：n2 2mn8m2 6m10，即 n(2m1)  n(4m1)  0, n 2m1或n (4m1) ...............................................................................10分 所以当n2m1时，直线PQ为：ymx2m1，恒过点A（2，1）,不符合题意； 当n(4m1)时，直线PQ为：ymx4m1，即y1m(x4)，恒过点（4，1）， 综上，直线PQ恒过定点(4，1) .................................................................................12分 方法二：设过点A的直线为y 1  k(x  2)与y  tx2(t  0)相切， y 1  k(x  2)   tx2  kx  2k 1  0    k2  4t(2k 1） 0 y  tx2 数学 第 6 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}   k 1  k 2  8t  k 1  k 2  2，(k，k 分别是直线PA和QA的斜率）.......6分 k k  4t k k 1 2 1 2 1 2 设直线 PQ ：m(x  2)  n(y 1)  1 ...........................7分 椭圆方程：（ x  2)  2 2  2  (y 1) 1 2  6 联立得： （x  2)2  4(x  2)  m(x  2)  n(y 1)   2(y 1)2  4(y 1)  m(x  2)  n(y 1)   0 同除以(x  2)2得:(2  4n)( y 1 )2  4(m  n)( y 1 ) 1 4m  0 ..........9分 x  2 x  2 y 1 而 为(x, y)与(  2，1)连线的斜率 x  2 k  k 4(m  n) 即 1 2   2,即6m  2n 1代入直线方程得 k k 4m 1 1 2 （2n 1)(x  2)  6n(y 1)  6， 即(2n 1)x  6ny  2n  4  0 .........................................................11分  直 线 PQ恒 过 (4，1). .........................................................12分 数学 第 7 页 {#{QQABJYIUggCIABAAARgCAQEwCgCQkAECAKgOxAAEoAABiAFABAA=}#}