文档内容
绝密 ★ 启用前
2024 年普通高等学校招生全国统一考试(新课标 I 卷)
数学
本试卷共10页,19小题,满分150分.
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考
证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试
卷、草稿纸和答题卡上的非答题区域均无效.
3.填空题和解答题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草
稿纸和答题卡上的非答题区域均无效.
4.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有
一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1. 已知集合 ,则 ( )
.
A B. C. D.
.
2 若 ,则 ( )
A. B. C. D.
3. 已知向量 ,若 ,则 ( )
A. B. C. 1 D. 2
4. 已知 ,则 ( )
A. B. C. D.5. 已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为 ,则圆锥的体积为( )
A. B. C. D.
6. 已知函数 在R上单调递增,则a的取值范围是( )
A. B. C. D.
7. 当 时,曲线 与 的交点个数为( )
.
A 3 B. 4 C. 6 D. 8
8. 已知函数 的定义域为R, ,且当 时 ,则下列结论中一定
正确的是( )
A. B.
C. D.
二、选择题:本题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的选项中,有多项符合
题目要求. 全部选对得 6 分,部分选对的得部分分,选对但不全的得部分分,有选错的得 0
分.
9. 随着“一带一路”国际合作的深入,某茶叶种植区多措并举推动茶叶出口.为了解推动出口后的亩收入
(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 ,样本方差
,已知该种植区以往的亩收入 服从正态分布 ,假设推动出口后的亩收入 服从
正态分布 ,则( )(若随机变量Z服从正态分布 , )
A. B.
C. D.
10. 设函数 ,则( )A. 是 的极小值点 B. 当 时,
C. 当 时, D. 当 时,
11. 设计一条美丽的丝带,其造型 可以看作图中的曲线C的一部分.已知C过坐标原点O.且C上的点
满足:横坐标大于 ,到点 的距离与到定直线 的距离之积为4,则( )
A. B. 点 在C上
C. C在第一象限的点的纵坐标的最大值为1 D. 当点 在C上时,
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. 设双曲线 的左右焦点分别为 ,过 作平行于 轴的直线交C于A,B
两点,若 ,则C的离心率为___________.
13. 若曲线 在点 处的切线也是曲线 的切线,则 __________.
14. 甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡
片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选
一张,并比较所选卡片上数字的大小,数字大的人得 1分,数字小的人得0分,然后各自弃置此轮所选的
卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为_________.
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. 记 的内角A、B、C的对边分别为a,b,c,已知 ,
(1)求B;(2)若 的面积为 ,求c.
16. 已知 和 为椭圆 上两点.
(1)求C的离心率;
(2)若过P的直线 交C于另一点B,且 的面积为9,求 的方程.
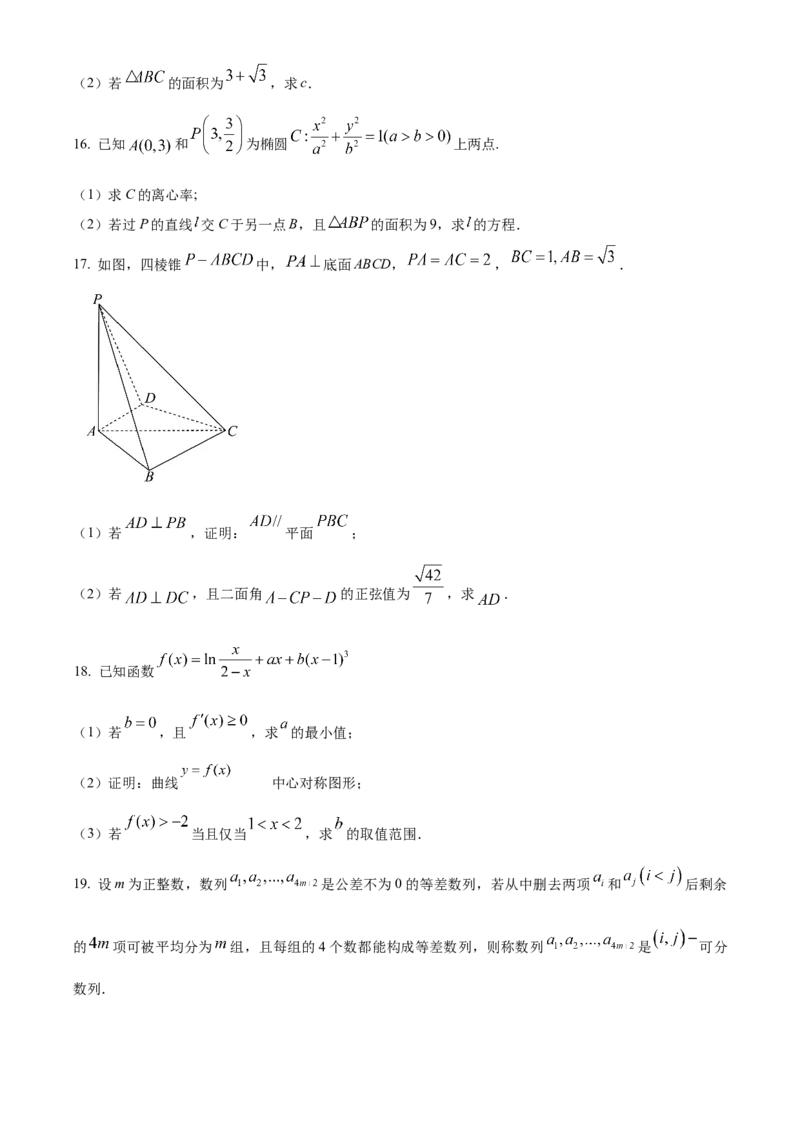
17. 如图,四棱锥 中, 底面ABCD, , .
(1)若 ,证明: 平面 ;
(2)若 ,且二面角 的正弦值为 ,求 .
18. 已知函数
(1)若 ,且 ,求 的最小值;
是
(2)证明:曲线 中心对称图形;
(3)若 当且仅当 ,求 的取值范围.
19. 设m为正整数,数列 是公差不为0的等差数列,若从中删去两项 和 后剩余
的 项可被平均分为 组,且每组的4个数都能构成等差数列,则称数列 是 可分
数列.(1)写出所有 的, ,使数列 是 可分数列;
(2)当 时,证明:数列 是 可分数列;
(3)从 中一次任取两个数 和 ,记数列 是 可分数列的概率
为 ,证明: .