2026届高三第3次月考（教师版）(1)_2026年1月_260103海南省海口市海南中学2025-2026学年高三上学期12月月考

海南中学 2026 届高三年级第三次月考数学试题 时间：120 分钟 满分：150 分 命题、审核：李园、杨菲 一、单项选择题：本题共8 小题，每小题5 分，共40 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1．若复数za23a22a4iaR为纯虚数，则a（ ） A．2 B．1 C．0 D．1 或2 【答案】B a23a20 【详解】由题意可得： ，解得：a1. 2a40 2．已知集合A x 0 x2  ，B x1 x3  ，则AC B=（ ） R A． 0,1  B．0,1 C．2,3 D． 2,3  【答案】A 【详解】由B x1 x3  ，则C B {x|x1或x3，又A x 0 x2  ，则AC B (0,1]. R R 3．不等式 2x11的一个充分不必要条件是（ ） 1 1 1 A．  x B．0x1 C．1 x2 D．1 x 3 2 2 【答案】A 【详解】对于B：由 2x11得12x11，解得0x1，显然0x1为充要条件，错误； 1 1 1 1 对于A：因为  x 能推出0x1，0x1不能推出  x ， 3 2 3 2 1 1 所以  x 是不等式 2x11的充分不必要条件，正确； 3 2 对于C：因为1 x2不能推出0x1，0x1能推出1 x2， 所以1 x2是不等式0x1的必要不充分条件，错误； 第 1 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 1 1 对于D：因为1 x 不能推出0x1，0x1不能推出1 x ， 2 2 1 所以1 x 是不等式0x1的既不充分也不必要条件，错误. 2        4．△OAB，点P在边AB上，AB3AP，设OAa,OBb，则OP=（ ） 1 2 2 1 A． a b B． a b 3 3 3 3 1 2 2 1 C． a b D． a b 3 3 3 3 【答案】B     1  1    2 1 2  1  【详解】依题意，OPOAAPOA ABOA OBOA  OA OB a b. 3 3 3 3 3 3     1 5．已知ABC所在平面内的动点M满足AM  xAC yAB，且实数x，y形成的向量a(x ,y) 2  与b(1,2)向量共线，则动点M的轨迹必经过ABC的（ ） A．垂心 B．内心 C．外心 D．重心 【答案】D  1   1 【详解】a(x ,y)与b(1,2)向量共线，故2x  y0，即2xy1， 2  2 则  A  M   x  A  C   y  A  B  变形为  A  M   x  A  C  12x  A  B  ，即  A  M    A  B  x   A  C  2  A  B   ，          所以BM x BCAB x BCBA ，   取AC的中点E，则BM 2xBE，所以动点M的轨迹必经过ABC的重心. 6．若函数 f xexax在区间 0,1 上有极值点，则实数a的取值范围是（ ） A．  0, 1  B．  1,e2 C．1,e D．  0, 1   2  e 【答案】C 【详解】由已知得 fxex a，明显 fx 为单调递增函数， 若函数 f xexax 在0,1上有极值点， 则e0a0且ea0，解得1ae.即a1,e. 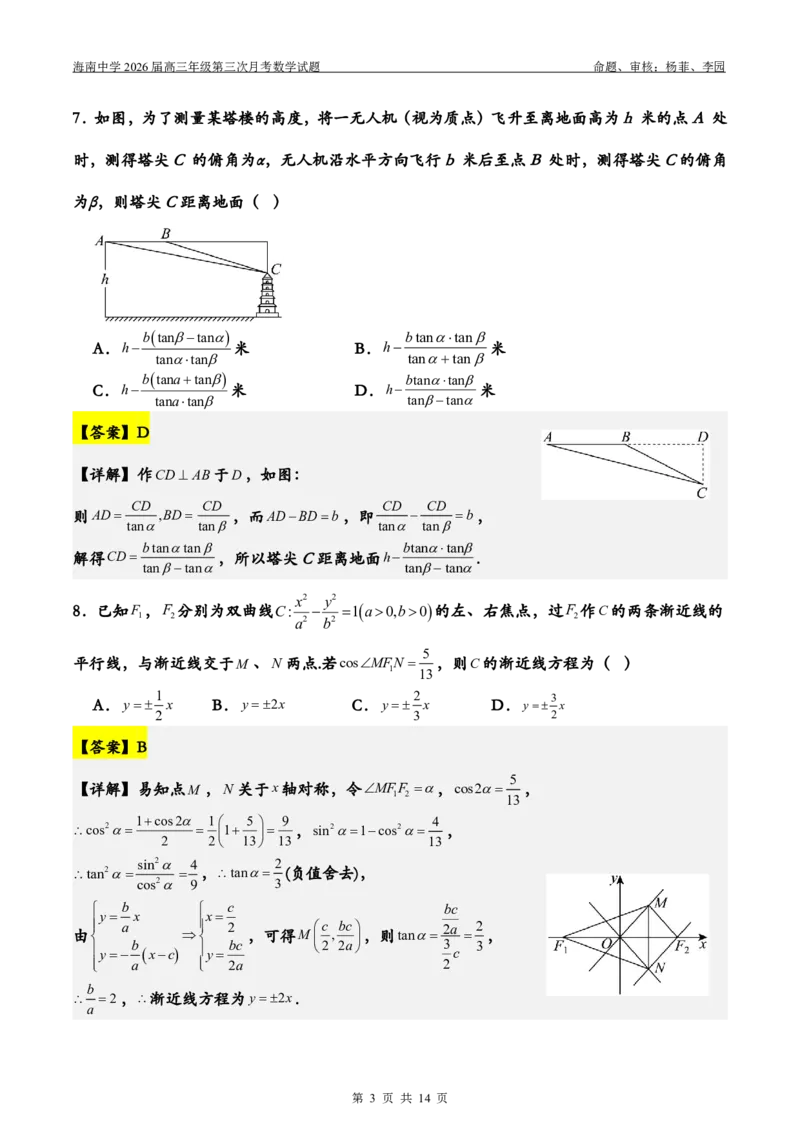第 2 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 7．如图，为了测量某塔楼的高度，将一无人机（视为质点）飞升至离地面高为h 米的点A 处 时，测得塔尖C 的俯角为α，无人机沿水平方向飞行b 米后至点B 处时，测得塔尖C的俯角 为β，则塔尖C距离地面（ ） btantan btantan A．h 米 B．h 米 tantan tantan btanatan btantan C．h 米 D．h 米 tanatan tantan 【答案】D 【详解】作CD AB于D，如图： CD CD CD CD 则AD ,BD ，而ADBDb，即  b， tan tan tan tan btantan btantan 解得CD ，所以塔尖C距离地面h . tantan tantan x2 y2 8．已知F ，F 分别为双曲线C:  1  a0,b0 的左、右焦点，过F 作C的两条渐近线的 1 2 a2 b2 2 5 平行线，与渐近线交于M 、N两点.若cosMFN  ，则C的渐近线方程为（ ） 1 13 1 2 3 A．y x B．y2x C．y x D．y x 2 3 2 【答案】B 5 【详解】易知点M ，N关于x轴对称，令MFF ，cos2 ， 1 2 13 1cos2 1 5  9 4 cos2  1  ，sin21cos2 ， 2 2 13 13 13 sin2 4 2 tan2  ，tan (负值舍去)， cos2 9 3  b  c bc y x x    a  2 c bc 2a 2 由  ，可得M , ，则tan  ，  y b xc  y bc 2 2a 3 c 3  a  2a 2 b  2，渐近线方程为y2x. a 第 3 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 二、多项选择题：本题共3 小题，每小题6 分，共18 分.在每小题给出的选项中，有多项符合 题目要求.全部选对的得 6 分，部分选对的得部分分，有选错的得 0分. 9．下列说法正确的是（ ） A．过点 1,2 且垂直于直线x2y30的直线方程为2xy0 B．过点P1,2且在x、y轴上截距相等的直线方程为2xy0 C．曲线x2 1 y0过点  0, 1 的最短弦长为 1 2  8 2 D．已知圆C :x12 y2 1，圆C :x42 y2 a，若两圆公切线有三条，则a4且其中一 1 2 条公切线的方程为x2 【答案】ACD 【详解】对于A：与直线x2y30垂直的直线斜率为2，故所求直线为y22(x1)， 即2xy0，故A 正确； x y 1 2 对于B：若截距都不为0时，令直线为  1a0，则  1，解得a3， a a a a 此时直线方程为x y30，若截距都为0时，令直线为ykx，则k 2，此时直线方程为2xy0， 过点P1,2且在x、y轴上截距相等的直线方程为2xy0或x y30，故B 错误； 1 1  1 对于C：曲线x2 y0，即x2  y，所以抛物线的焦点为0, ， 2 2  8 故过点  0, 1 的最短弦为通径，长度为 1 ，故C正确；  8 2 对于D：因为圆C :x12 y2 1的圆心为C 1,0，半径r 1， 1 1 1 圆C :x42 y2 a的圆心为C 4,0，半径r  a ， 2 2 2 若两圆公切线有三条，则两圆相外切，则CC 3r r  a 1，解得a4， 1 2 2 1   x12y21 x2 由 ，解得 ，即两圆的切点为2,0，  x42y24 y0 显然x2与圆C :x12 y2 1，圆C :x42y2 4均相切，故x2是两圆的公切线，故D正确. 1 2 第 4 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园   10．已知向量a1,1 ，b 1,x，下列结论正确的是（ ）   A．若ab，则x1   B．若a∥b，则x1   C．若a，b的夹角为钝角，则x的取值范围为 ,1     D．设a在b方向上的投影向量为m，则 m的取值范围为  0, 2  【答案】AD   【详解】因为向量a1,1 ，b 1,x，     对于选项A：若ab，则ab1x0，解得x1，故A 正确；   1 x 对于选项B：若a//b，则  ，即x1，故B 错误； 1 1       对于选项C：由a,b的夹角为钝角，则ab1x0，且a,b不共线， 可得x1且x1，所以x的取值范围为 ,11,1 ，故C 错误；   对于选项D：因为a  b  1x， b   x21，则 m   a  b  1x ，可得 m  2  x22x1 ， b 1x2 1x2 令 x22x1 t，则 1tx22x1t0， 1x2 当1t 0，即t 1时，可得x0，符合题意； 当1t0，即t1时，则Δ441t2 0，解得0t2且t1，  综上所述：0t2，即 m的取值范围为0, 2，故D正确.   π 11. 在ABC中，内角A，B，C所对的边分别为a，b，c，ABC  ，内角B的平分线交AC 3 于点D且BD  3，则下列结论正确的是（ ） 1 1 A.  1 B. b的最小值是2 a c C. a3c的最小值是4 3 D. ABC的面积最小值是 3 【答案】ABD 【详解】解：由题意得：S S S ， △ABC △ABD △BCD 第 5 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 1  1  1  由角平分线以及面积公式得 acsin  3asin  3csin ， 2 3 2 6 2 6 1 1 化简得ac ac，所以  1，故A 正确； a c acac 2 ac ，当且仅当ac时取等号， ac 2，ac4， 1 3 所以S  acsinABC ac 3 ，当且仅当ac2时取等号，故 D正确； ABC 2 4 由余弦定理b2 a2 c2 2accosABC a2 c2 ac  ac 2 3ac ac 2 3ac42 344 所以b2，即b的最小值是2，当且仅当ac2时取等号，故B 正确； 1 1 对于选项C：由ac ac得：  1， a c 1 1 a 3c a 3c a3c(a3c)(  )1  342  42 3， a c c a c a 1 1  1 a 1 3  a c  当且仅当 ，即 时取等号，故 C 错误． 3  a 3c c1  c a  3 三．填空题：本题共 3小题，每小题 5 分，共15 分. 12．若log 3a,2b 5，则用a,b表示log 15 . 2 6 ab 【答案】 1a log 15 log 3log 5 ab 【详解】因为2b 5，所以blog 5，则log 15 2  2 2  . 2 6 log 6 log 2log 3 1a 2 2 2 13．“莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形，它在很多特殊领域发挥了超 常的贡献值．“莱洛三角形”是分别以正三角形的顶点为圆心，以其边长为半径作圆弧，由这 三段圆弧组成的曲边三角形（如图所示）．现以边长为4 的正三角形作一个“莱洛三角形”，则 此“莱洛三角形”的面积为__________. 【答案】8π8 3 1 π π 4π 【详解】正三角形的面积为 42sin 4 3，圆弧的长度为l  4 ，故一个弓形的面积为 2 3 3 3 1 8π 8π  4l4 3 4 3，故“莱洛三角形”的面积为3 4 34 38π8 3. 2 3  3  第 6 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 14. 若在曲线yxeax1（e 为自然对数的底数）存在不同的两点P、Q，使P、Q两点关于x轴 的对称点P'、Q'在曲线 ylnxax上，则实数a的取值范围是__________. 1 【答案】( ,0) e2 【详解】已知函数 f(x) xeax1与g(x)lnxax的图象上存在关于x轴对称的点，那么 f(x) g(x)有解，即xeax1 lnxax在(0,)上有解， 首先对xeax1 lnxax进行变形：xeax1 lnxlneax ln(xeax). t 设t  xeax（t>0），则原方程变为 lnt. e t 进一步转化为lnt 0在(0,)上有解. e t 1 1 et 设 f(t)lnt ，对 f(t)求导，可得 f(t)   . e t e te et 然后分析 f(t)的单调性：令 f(t)0，即 0，解得t e. te 当00， f(t)在(0,e)上单调递增. 当t e时，所以 f(t)0， f(t)在(e,)上单调递减. e 所以 f(t)在t e处取得极大值，也是最大值， f(e)lne 110 . e 所以仅t e满足方程有解的条件. e 故xeax e有两解，即eax  有两解， x 1lnx 两边同时取对数得ax1lnx，即a  在(0,)上有两解. x 1 1lnx  x(1lnx) 设g(x) x ，对g(x)求导，则 g(x) x  lnx2 . x2 x2 lnx2 然后分析g(x)的单调性：令g(x)0，即 0，解得xe2. x2 当0e2时， g(x)>0，g(x)在(e2,)上单调递增. 1lne2 1 g(x)在xe2处取得极小值，也是最小值，g(e2)  . e2 e2 当x0时，g(x)；当x时，g(x)0. 1lnx 1 1 因为a  在(0,)上有两解， a0.故答案为：( ,0). x e2 e2 四．解答题：本题共 5小题，共 77 分，解答应写出文字说明、证明过程或演算步骤.      15.（13 分）设向量a (sinx,cosx),b (cosx,cosx),xR，函数 f(x)a(ab)． (1)求函数 f(x)的最大值与最小正周期； 3 (2)求使不等式 f(x) 成立的x的取值集合及函数 f(x)的对称中心． 2        解：（1）由题意知， f(x)a(ab)aaabsin2xcos2xsinxcosxcos2x 1 1 3 2   1 sin2x (cos2x1)  sin2x ， 2 2 2 2  4 3 2   即 f x  sin2x ， …………4 分 2 2  4     当2x  2k，即x k(kZ)时，sin(2x ) 1， 4 2 8 4 max 3 2 2 f(x)的最大值为 f x   ，最小正周期T  ． …………7 分 max 2 2 2 3 2   （2）由（1）知， f x  sin2x ， 2 2  4 3 3 2  3   f(x) ，即  sin(2x ) ，即sin(2x )0， …………8 分 2 2 2 4 2 4  2k2x 2k，kZ， 4  3 解得k  xk ，kZ， …………10 分 8 8 3   3  即 f(x) 成立的x的取值集合是x|k xk ,kZ． …………11分 2  8 8    k 令2x k，则x  ，kZ， 4 8 2  k 3 f(x)的对称中心为(  , )，kZ. …………13分 8 2 2 第 8 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 16．（15 分）21 世纪某次机器人展览会上，已知某公司共有 25 个汽车模型，其外观和内饰的 颜色分布如下表所示： 内饰 红色外观 蓝色外观 外观 棕色内饰 10 10 米色内饰 2 3 (1)若小明从这些模型中随机拿一个模型，记事件A为小明取到红色外观的模型，事件B为小 明取到棕色内饰的模型，求PB和P  B A  ，并判断事件A和事件B是否独立并说明理由. (2)该公司举行了一个抽奖活动，规定在一次抽奖中，每人可以从这些模型中拿两个汽车模型， 给出以下假设： 假设1：拿到的两个模型会出现三种结果，即外观和内饰均为同色，外观和内饰都异色，以及 仅外观或内饰同色. 假设2：按抽奖的可能性大小，概率越小奖金越高 假设3：该抽奖活动的奖金额为：一等奖800 元，二等奖500 元，三等奖 300元 请你分析奖金对应的结果，设X为奖金额，写出X的分布列并求出X的数学期望. 20 4 10 5 解:（1）PB  ，PB|A  ， 25 5 12 6 10 12 20 48 因为pAB ，PAP B   ， 25 25 25 125 有PAB PAPB，所以A，B不独立； …………6 分 （2）记外观与内饰均同色为事件A，外观与内饰都异色为事件A ，仅外观或仅内饰同色为事 1 2 件A ， 3 第 9 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 C2 C2 C2 C2 94 47 则P(A) 10 10 2 3   ， …………8 分 1 C2 300 150 25 C1C1C1C1 50 1 P(A ) 10 3 10 2   ， …………10 分 2 C2 300 6 25 C1C1C1C1C1C1 C1C1 156 13 P(A ) 10 2 10 3 10 10 2 3   ， …………12 分 3 C2 300 25 25 PA PAPA  ， 2 1 3 ∴一等奖800 元为两个汽车模型的外观与内饰都异色，二等奖 500 元为两个汽车模型的外观与 内饰均同色，三等奖 300 元为两个汽车模型仅外观或仅内饰同色． …………13 分 X的分布列为： X 800 500 300 1 47 13 P 6 150 25 …………14 分 1 47 39 EX800 500 300 446 ． …………15 分 6 150 75 第 10 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 a2(bc)2 17.（15 分）已知a,b,c分别为锐角ABC三个内角A,B,C 的对边，ABC的面积S  ， 2 （1）求sin A，cosA的值； b2c （2）求 的取值范围. a a2(bc)2 1 解:（1）在ABC中，由S  及三角形面积公式S  bcsin A， 2 2 a2 (b2 2bcc2) bcsin A 得  ，即2bc(b2 c2 a2)bcsin A， 2 2 由余弦定理得2bc(1cosA)bcsinA，即2(1cosA)sin A …………3 分 两边平方得4(12cosAcos2 A)sin2 A，即4(12cosAcos2 A)1cos2 A，………5 分 3 即5cos2 A8cosA30，解得cosA1或cosA 5 3 4 而0 A，有1cosA1，sin A0，则cosA ，sinA . …………7 分 5 5 （2）由正弦定理及ABC 得， 4 3 cosC sinC2sinC b2c sinB2sinC sin(AC)2sinC 5 5    a sinA sinA 4 5  13sinC4cosC  185 sin(C )，其中锐角由sin 4 ,cos 13 确定，………10 分 4 4 185 185  π 0C   2 π π π π 而ABC为锐角三角形，则 ，即 AC ， AC ， π  AC π 2 2 2 2 2 π 13 显然sin(C)1，而sin( )cos ， …………12 分 2 185 π 3 13 4 4 11 13 sin( A)cos(A)       ， 2 5 185 5 185 185 185 11 11 b2c 185 因此 sin(C)1，   ， 185 4 a 4 b2c 11 185 所以 的取值范围是( , ]. …………15 分 a 4 4 第 11 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 x2 y2 18．（17 分）已知椭圆E：  1ab0，以椭圆E的焦点和短轴端点为顶点的四边形是 a2 b2 边长为2 的正方形.已知斜率k存在且不为 0 的直线l过点0,t t  2  ，直线l与椭圆E交于不同 1 的两点A,B，过点A和C(0, )的直线AC与椭圆E的另一个交点为D． 2 (1)求椭圆E的方程及离心率； (2)若直线BD的斜率为0，求t的值及斜率k 的取值范围． 2 解：（1）由题意bc  2，从而a b2c2 2， 2 x2 y2 2 所以椭圆方程为  1，离心率为e ； …………5 分 4 2 2 （2） 设AB:y kxt,  k 0,t  2  ，Ax ,y ,Bx ,y ， 1 1 2 2 x2 y2 联立   4  2 1 ，化简并整理得  12k2 x24ktx2t240， …………6 分  ykxt 由题意Δ16k2t28  2k21  t22  8  4k22t2  0 ，即k,t应满足4k22t2 0， …………7 分 4kt 2t24 所以x x  ,xx  ， …………8 分 1 2 12k2 1 2 2k21 若直线BD斜率为 0，由椭圆的对称性可设Dx ,y ， …………9 分 2 2 y y 所以AD:y 1 2 xx  y ，在直线AD方程中令x0， …………10 分 x x 1 1 1 2 x y x y x (kx t)x (kx t) 2kx x t(x x ) 4k(t2 2) 2 1 得y  1 2 2 1  1 2 2 1  1 2 1 2  t   ， …14 分 c x x x x x x 4kt t 2 1 2 1 2 1 2 所以t 4， …………15分  4k22t24k2140 14 14 此时k应满足 ，即k应满足k  或k  ， k0 2 2 14 14 综上所述，t 4满足题意，此时k  或k  . …………17 分 2 2 第 12 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 19．（17 分）已知函数 f(x)ex cosx2， f(x)为 f(x)的导数. (1)当x0时，求 f(x)的最小值； π (2)当x 时，xexxcosxax22x0恒成立，求a的取值范围. 2 解:（1）由题意， f(x)exsinx ， 令g(x)exsinx，则g(x)excosx， 当x0时，ex 1，cosx1，所以g(x)0，从而g(x)在[0,)上单调递增， 则g(x)的最小值为g(0)1，故 f(x)的最小值1； …………5 分 π （2）由已知得当x 时，x  ex cosxax2 0恒成立， 2 令hxexcosxax2，hxexsinxa， …………6 分 ①当a1时，若x0时，由（1）可知hx1a0，∴hx 为增函数， ∴hxh00恒成立，∴xhx0恒成立，即x  ex cosxax2 0恒成立， …………8 分  π  若x   ,0，令mxexsinxa 则mxex cosx，  2  令nxex cosx，则nxexsinx ， 令pxexsinx，则pxex cosx，  π   π  ∵在px在x   ,0内大于零恒成立，∴函数px 在区间   ,0为单调递增，………10分  2   2  又∵p   π e  π 210， p  0 1，，  2  π  ∴px 上存在唯一的x  ,0使得 px 0， 0  2  0  π  ∴当x    2 ,x 0   时，nx0，此时nx为减函数， 当xx ,0时，nx0，此时nx为增函数， 0 又∵n   π e  π 2 0，n00，  2  π  ∴存在x  ,x ，使得nx 0， ………12 分 1  2 0 1  π  ∴当x    2 ,x 1 时，mx0，mx 为增函数，当xx 1 ,0时，mx0，mx 为减函数， 第 13 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}海南中学2026届高三年级第三次月考数学试题 命题、审核：杨菲、李园 又∵m   π e  π 21a0，m01a0，  2  π  ∴x   ,0时，hx0，则hx 为增函数，∴hxh00，  2  ∴x  ex cosxax2 0恒成立， ………14 分 ②当a1时，m(x)ex cosx0在[0,)上恒成立，则mx 在[0,)上为增函数， ∵m01a0，m(ln(1a))eln(1a)sin(ln(1a))a1sin(ln(1a))0 ， ∴存在唯一的x 0,使hx 0， 2 2 ∴当0xx 时，h(x)0，从而h(x)在  0,x 上单调递减， 2 2 ∴hxh00， ∴x  excosxax2 0，与xexxcosxax22x0矛盾， 综上所述，实数a的取值范围为(,1]. ………17分 第 14 页 共 14 页 {#{QQABBQa0wgIQgIbACT5qB0WkCwqYkJChLAgExVAcOAYjgRFAFIA=}#}