文档内容
2024—2025 学年高三年级学科素养检测(三
数 学
学校 班级 调) 姓名 考号
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号
涂 黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案
写在 答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:函数与导数、数列、三角函数与解三角形占70%,平面
向 量、复数、直线与圆占30%。
弥 封 不 要 答
题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合 题目要求的
1.若集合A={x|y= √x},B={x|y=log (5-x)}, 则A∩B=
3
A. (5,十∞) B.(0,5)
C.(0,+) D.(0,5)
2.在平行四边形ABCD中,AB=2AE,BF=2BC,则EF=
D.2AB+2AD
3.若曲线 在点(1,1)处的切线与圆C:(x-5)²+(y-1)²=9 相交于A,B 两点,
则 |AB|=
A.1 B.2
C.√2 D.2√2
4.为了让自己渐渐养成爱运动的习惯,小明10月1日运动了5分钟,从第二天开始,每天
运动
的时长比前一天多2分钟,则从10月1日到10月的最后一天,小明运动的总时长为
A.1000 分钟 B.1022 分钟
C.1065 分钟 D.1085 分钟
5.“x> 3.1”是“x>-log 0.5”的
0.5 256
A.充分不必要条件 B.必要不充分条件
C. 充要条件 D.既不充分也不必要条件
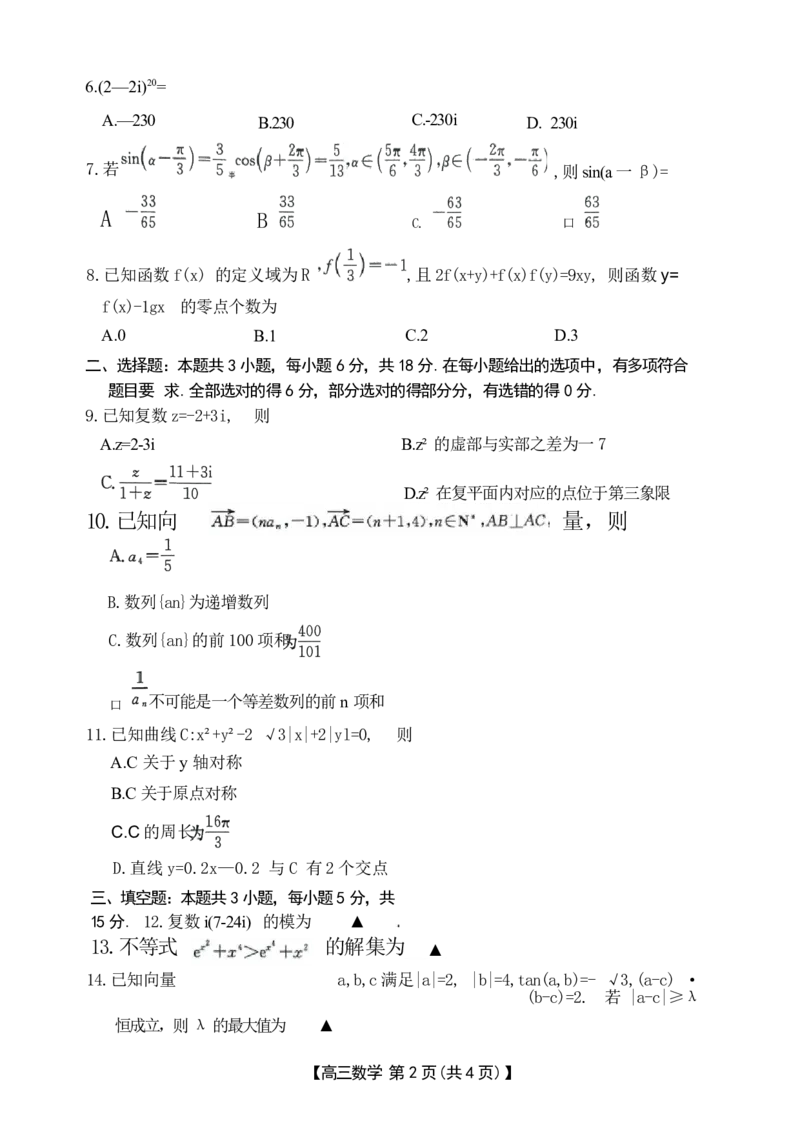
【高三数学第1页(共4页)】6.(2—2i)20=
A.—230 B.230 C.-230i D. 230i
7.若 ,则sin(a一β)=
事
A B
C. 口
8.已知函数f(x) 的定义域为R ,且2f(x+y)+f(x)f(y)=9xy, 则函数y=
f(x)-1gx 的零点个数为
A.0 B.1 C.2 D.3
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要 求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数z=-2+3i, 则
A.z=2-3i B.z² 的虚部与实部之差为一7
D.z² 在复平面内对应的点位于第三象限
10.已知向 量,则
B.数列{an}为递增数列
C.数列{an}的前100项和
口
不可能是一个等差数列的前n 项和
11.已知曲线C:x²+y²-2 √3|x|+2|yl=0, 则
A.C 关于y 轴对称
B.C 关于原点对称
C.C的周长
D.直线y=0.2x—0.2 与C 有2个交点
三、填空题:本题共3小题,每小题5分,共
15分. 12.复数i(7-24i) 的模为 ▲
13.不等式 的解集为
▲
·
14.已知向量 a,b,c满足|a|=2, |b|=4,tan(a,b)=- √3,(a-c) ·
(b-c)=2. 若 |a-c|≥λ
恒成立,则λ的最大值为 ▲
·
【高三数学 第2页(共4页)】四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步
骤. 15. (13分)
已知函数f(x)=8sin(4x+φ)(0<φ<
π)的图象关于点 对称.
(1)求φ;
(2)求f(x) 上的值域;
(3)将f(x) 图象上所有点的横坐标变为原来的两倍,纵坐标不变,得到函数g(x) 的图
象, 求g(x) 的最小正周期与单调递减区间.
16. (15分)
已知函数
(1)判断f(x) 的奇偶性,并说明理由;
(2)若不等式 f(一4x+ m ·2x)+f (一14)< 0 对x∈R 恒成立,求m 的取值范围.
17. (15分)
在 △ABC中 ,AC=10,sin C=2sin A
(1)若 ,求△ABC 的周长;
(2)求△ABC 的面积的最大值.
【高三数学第3页(共4页)】18.(17分)
已知等比数列{an}的前n项和为
(1)求{an}的通项公式;
求数列{bn}的前n 项和T ;
n
(3)若存在正整数n, 使得(S -m)(S -m)<0 成立,求m 的取值范围.
n n+1
密 封
题
19.(17分)
f(x)与 g(x)的定义域的交集为 D.若 f(x)g(x)≥0 对 x ∈D 恒成
已知函数
立 , 则 称 f(x) 与 g(x) 为 同 号 函 数 , 例 如
则函数f(x)
为同号函数.若存在区间[m,m+2], 使得f(x) g(x) ≥0 对x∈ [m,m+2] 恒成立,
则称f(x) 与g(x) 为区间同号函数.
(1)设函数f₁(x)=(x²-4x+3)ex(0