云南大理市辖区2023-2024学年高三上学期毕业生区域性规模化统一检测数学答案(1)_2023年9月_029月合集_2024届云南省大理市辖区高三区域性规模化统一检测

大理市辖区 2024 届高中毕业生区域性规模化统一检测 数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分） 题号 1 2 3 4 5 6 7 8 答案 C A A C D D B B 【解析】 1．由 A{2，4，6}，∴( A)B{2}，故选C． U U 2．a2i1bi，∴a1，b2，∴z12i，∴z12i，故选A． 3．令x1得a a a a a a 0，故选A． 0 1 2 3 4 5 4．由方程知，渐近线方程为y 3x，它们交成的两对对顶角为60和120，所以两条渐近 线的夹角为60，故选C． 2x 1 5．注意到函数 f(x)的定义域为R，且g(x) 是奇函数，所以只需h(x)sinxm为奇函 2x 1 2x 1 数，h(0)0得m0．反之，当m0时，显然 f(x)sinx 是偶函数，故选m0， 2x 1 故选D． 6．记事件A表示“小孩诚实”，事件B表示“小孩说谎”，已知P(B|A)0.1，P(B|A)0.5， P(A)0.9，P(A)0.1，P(B)P(AB)P(AB)P(A)P(B|A)P(A)P(B|A)0.90.1 P(AB) 9 0.10.50.14，P(AB)P(A)P(B|A)0.90.10.09，P(A|B)  ，故选D． P(B) 14 f(a ) 2a +1 7．对于 A： n1  n1 常数，所以 f(x)2x1不是保等比数列函数；对于 B： f(a ) 2a +1 n n 1 f(a ) |a | |a | 1 n1  n1 = n =|q| 为常数，所以 f(x) 是保等比数列函数；对于 C： f(a ) 1 |a | |x| n n1 |a | n f(a ) ean1 n1  ean1an  常数，所以 f(x)ex 不是保等比数列函数；对于 D： f(a ) ean n f(a ) log |a | log |a q| log |q| n1  3 n1  3 n 1 3 常数，所以 f(x)log |x|不是保等比数 f(a ) log |a | log |a | log |a | 3 n 3 n 3 n 3 n 列函数，故选B． 数学参考答案·第1页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}x 8．易知函数y1cos 的周期为4π，所以圆柱的底面圆的周长为4π，所以圆的直径为4， 2 x 据题意可知该椭圆的短轴长为2b4，所以b2，又函数y1cos 的最大值为2，所以 2 1 5 椭圆的长轴长为2a 42 22 2 5a 5c1，所以椭圆的离心率e  ， 5 5 故选B． 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有 多项是符合题目要求的．全部选对的得5分，部分选对的得2分，有选错的得0分） 题号 9 10 11 12 答案 AD ACD BC ABD 【解析】 235911 1210a73 32a 9．由表格数据得，x 6， y  ，将样本中心点 5 5 5  6， 32a  代入回归直线方程 y110.5x得， 32a 110.56，解得a8，则样本中  5  5 心点为(6，8)，所以选项 A 正确；对选项 B，当变量x增加，变量y相应值减少，两个变 量之间呈负相关关系，所以选项B错误；对选项C，由经验回归方程 y110.5x，令x7， 得预测值 y7.5，而预测值不一定等于观测值，所以选项C错误；对选项D，由残差定义 知，观测值减去预测值为残差．由经验回归方程 y110.5x，令x11，得预测值 y5.5， 则相应于(11，3)的残差为35.52.5，所以选项D正确，故选AD． 10．∵12a 3，12b 4，∴alog 30，blog 40，∴ablog 3log 4log 121， 12 12 12 12 12 b log 4 ab 2 1 对于A：  12 log 4log 31，所以A正确；对于B：ab   ，故B a log 3 3 3  2  4 12 1 1 错误；对于 C：∵a2 b2 (ab)2 2ab12ab12  ，故 C 正确；对于 D： 4 2 1 ∵ab2a11，∴2ab 21  ，故D正确，故选ACD． 2 11．设切点为(x，y )，f(x)3x2 m，切线的方程为y(x3 mx )(3x2 m)(xx )，代入 0 0 0 0 0 0 点P(1，1)，可得1(x3 mx )(3x2 m)(1x )，即2x3 3x2 m1．因为切线过点 0 0 0 0 0 0 数学参考答案·第2页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}P(1，1)恰能作 3 条曲线 y f(x)的切线，所以方程2x3 3x2 m1有 3 解．令函数 0 0 g(x)2x3 3x2，g(x)6x(x1) ．当 x1或 x0 时， g(x)0 ；当 1x0 时， g(x)0，所以g(x)在(，1)和(0，)上单调递增，在(1，0)上单调递减，所以g(x) 的极大值为g(1)1，g(x)的极小值为g(0)0，所以0m11，解得1m2，故选 BC． 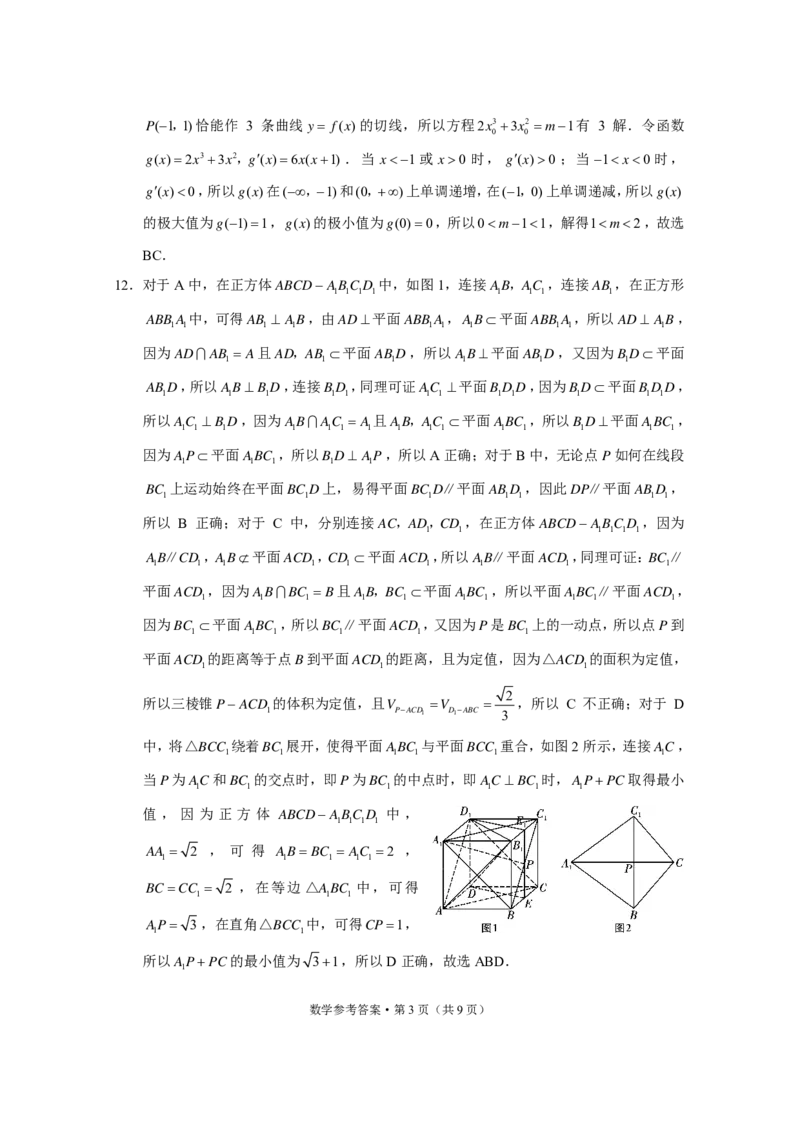12．对于A中，在正方体ABCDABCD 中，如图1，连接AB，AC ，连接AB ，在正方形 1 1 1 1 1 1 1 1 ABBA中，可得AB  AB，由AD平面ABBA，AB平面ABBA，所以AD AB， 1 1 1 1 1 1 1 1 1 1 因为ADAB  A且AD，AB 平面ABD，所以AB平面ABD，又因为BD平面 1 1 1 1 1 1 ABD，所以ABBD，连接BD ，同理可证AC 平面BDD，因为BD平面BDD， 1 1 1 1 1 1 1 1 1 1 1 1 所以AC BD，因为ABAC  A且AB，AC 平面ABC ，所以BD平面ABC ， 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 因为AP平面ABC ，所以BD AP，所以A正确；对于B中，无论点P如何在线段 1 1 1 1 1 BC 上运动始终在平面BCD上，易得平面BCD∥平面ABD ，因此DP∥平面ABD ， 1 1 1 1 1 1 1 所以 B 正确；对于 C 中，分别连接AC，AD，CD ，在正方体ABCDABCD ，因为 1 1 1 1 1 1 AB∥CD ，AB平面ACD ，CD 平面ACD ，所以AB∥平面ACD ，同理可证：BC∥ 1 1 1 1 1 1 1 1 1 平面ACD ，因为ABBC B且AB，BC 平面ABC ，所以平面ABC∥平面ACD ， 1 1 1 1 1 1 1 1 1 1 因为BC 平面ABC ，所以BC∥平面ACD ，又因为P是BC 上的一动点，所以点P到 1 1 1 1 1 1 平面ACD 的距离等于点B到平面ACD 的距离，且为定值，因为△ACD 的面积为定值， 1 1 1 2 所以三棱锥PACD 的体积为定值，且V V  ，所以 C 不正确；对于 D 1 PACD1 D1ABC 3 中，将△BCC 绕着BC 展开，使得平面ABC 与平面BCC 重合，如图2所示，连接AC， 1 1 1 1 1 1 当P为AC和BC 的交点时，即P为BC 的中点时，即AC BC 时，APPC取得最小 1 1 1 1 1 1 值 ， 因 为 正 方 体 ABCDABCD 中 ， 1 1 1 1 AA  2 ， 可 得 ABBC  AC 2 ， 1 1 1 1 1 BC CC  2 ，在等边△ABC 中，可得 1 1 1 AP 3，在直角△BCC 中，可得CP1， 1 1 所以APPC的最小值为 31，所以D正确，故选ABD． 1 数学参考答案·第3页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}三、填空题（本大题共4小题，每小题5分，共20分） 题号 13 14 15 16 24 f(x)x（答案不 7 答案 20500 25 唯一） 5 【解析】  4  4 sinA ， tanA ，   5 13 ． 由 题 设 知 ， 角 A 为 锐 角 ， 从 而  3 解 得  所 以 3  sin2 Acos2 A1， cosA ，  5 24 sin2A2sinAcosA ． 25 14．若 f(x)axb，则由 f(x2) f(x)2，得ax2abaxb2，得a1，与b无关．若 取b0，则 f(x)x，故填 f(x)x（答案不唯一）．       |ab|8， |a|2 |b|2 2ab64，①     15．由   得    解之得ab7，代入①得：|a|2 |b|250， |ab|6， |a|2 |b|2 2ab36，②          ab 7   ③，又|a||b|，代入③得：|a||b|5，所以|a|cosa，b   ，故a在b上投影向 |b| 5  7 b 7 7 量的模为   ，故填 ． 5|b| 5 5 16．由题意知，抛物线 C 过点 P(250，156.25) ，设抛物线 C：x2 2py(p0) ，所以 2502 2156.25p，解得：p200，即抛物线C的方程为x2 400y．所以，焦点F(0，100)， x2 400y， 156.25100 9 9  k   ；所以PQ的方程为y x100，联立方程组 9 消 PQ 250 40 40 y x100，  40 9 y 得 x2 90x400000，x x 90 ，所以 y  y  (x x )200220.25 ，所以 1 2 1 2 40 1 2 |004000| 4000 |PQ| y  y  p420.25．又原点 O 到直线PQ的距离d   ，所以 1 2 92 402 41 1 1 4000 △OPQ的面积为 |PQ|d  420.25 20500． 2 2 41 四、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分10分） 3 1 1  π 1 解：（1）由已知， f(x) 3sinxcosxsin2x sin2x cos2x sin2x  ， 2 2 2  6 2 数学参考答案·第4页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}3  π 1 3 ∵ f(A) ，∴ f(A)sin2A   ， 2  6 2 2  π 即sin2A 1，  6 π π 11π ∵0 Aπ，∴ 2A  ， 6 6 6 π π π ∴2A  ，∴A ． ………………………………………………………（5分） 6 2 3 （2）如图4，sinC2sinB，c2b， ∵AD平分BAC ， π ∴BADCAD ， 6 ∵S S S ， △ABD △ADC △ABC 图3 1 π 1 π 1 π ∴ c2sin  b2sin  bcsin ， 2 6 2 6 2 3 1 1 1 1 1 3 ∴ 2b2  b2  b2b ， 2 2 2 2 2 2 ∴b 3， 1 1 3 3 3 故△ABC的面积S  AB ACsinA  32 3  ． 2 2 2 2 ……………………………………………………………（10分） 18．（本小题满分12分） 解：（1）设等差数列{a }的首项为a ，公差为d 0， n 1 又a 是a 和a 的等比中项，得a2 aa ，即(a d)2 a (a 4d)， 2 1 5 2 1 5 1 1 1 即d 2a ，① 1 又a 2a 1(nN*)，取n1时，a 2a 1，即a d 2a 1，② 2n n 2 1 1 1 将①②联立解得a 1，d 2， 1 a 2n1． ……………………………………………………………（4分） n （2）因为ab a b a b (2n3)2n16， 1 1 2 2 n n 所以ab a b a b (2n5)2n 6(n≥2)， 1 1 2 2 n1 n1 两式相减得：a b (2n3)2n16(2n5)2n 6(2n1)2n(n≥2)， n n 又ab 2满足上式，所以a b (2n1)2n(nN*)， 1 1 n n 数学参考答案·第5页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}又a 2n1，所以b 2n． n n 所以T 12n 32n152n2 (2n3)4(2n1)2， n 2T 12n132n 52n1(2n3)8(2n1)4， n 两式相减得：T 2n12n12n 8(2n1)2 n 82n2 2n1 (2n1)232n14n6． ……………………………（12分） 12 19．（本小题满分12分） 1P(≤≤) 解：（1）由题意可知60，10，则P(70) 0.15865， 2 所以，这6人中至少有一人进入面试的概率P1(10.15865)6 0.6453． ……………………………………………………………（4分） （2）由题意可知，随机变量X 的可能取值有0，1，2，3， 1 1 1 1 3 1 1 1 2 1 1 1 1 6 则P(X 0)    ，P(X 1)          ， 4 3 2 24 4 3 2 4 3 2 4 3 2 24 3 2 1 1 2 1 3 1 1 11 3 2 1 6 P(X 2)          ，P(X 3)    ， 4 3 2 4 3 2 4 3 2 24 4 3 2 24 所以，随机变量X 的分布列如下表所示： X 0 1 2 3 1 6 11 6 P 24 24 24 24 1 6 11 6 46 23 故E(X)0 1 2 3   ． ………………（12分） 24 24 24 24 24 12 20．（本小题满分12分） （1）证明：连接AE，DE ，如图4， 因为PA平面ABCD，所以PA AB， 又BC CD，CDCE1，由勾股定理可知DE  2， 又ADBE，AD∥BE，所以四边形ABED是平行四边形， 所以ABDE  2， π 又ABC  ，由余弦定理可知AE 2， 图4 4 所以AB2  AE2 BE2，所以AB AE， 数学参考答案·第6页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}又AEPA A，所以AB平面PAE， 所以ABPE． ……………………………………………………………（6分） （2）解：因为AP，AB，AE两两垂直， 所以以A为原点建立如图所示空间直角坐标系Axyz， 则A(0，0，0)，B( 2，0，0)，D( 2， 2，0)，P(0，0，2)，E(0， 2，0)  2 2  因为F 为PD的中点，则F ， ，1，   2 2    设平面AEF 的法向量n(x，y，z )， 1 1 1   n AE  2y 0，  1 则  2 2 n AF  x  y z 0，  2 1 2 1 1 2   2 取x 1，则y 0，z  ，所以n1，0， ， 1 1 1 2  2      mDE  2x 0，   2 设平面DEF 的法向量m(x 2 ，y 2 ，z 2 )，则  2 2 M DF  x  y z 0，  2 2 2 2 2 2   2 取y 1，则x 0，z  ，所以m0，1， ， 2 2 2 2  2    1     |mn| 2 1 所以cosn，m     ． ……………………………（12分） |m||n| 1 1 3 1  1 2 2 21．（本小题满分12分） (x3)2  y2 3 （1）解：设M(x，y)，由题意得  ， 25 5 x 3 x2 y2 ∴  1为点M的轨迹C的方程． ……………………………………（4分） 25 16 （2）证明：方法1： 设A(x，y )，B(x，y )，由题知k 0，m0，N(x，y )且x 0，y 0， 1 1 2 2 0 0 0 0 |m| ∵直线l：ykxm与圆x2  y2 16相切，∴ 4，即m2 16(k2 1)， k2 1 数学参考答案·第7页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}x2 y2 把l：ykxm代入  1，得(25k2 16)x2 50kmx25m2 4000， 25 16 显然(50km)2 4(25k2 16)(25m2 400)14400k2 0， 50km 25m2 400 x x  ，xx  ， 1 2 25k2 16 1 2 25k2 16 120k k2 1 ∴|AB| k2 1|x x | ， 1 2 25k2 16 3 3 3 3 50km 30km |FA||FB|5 x 5 x 10 (x x )10  10 5 1 5 2 5 1 2 5 25k2 16 25k2 16 120k k2 1 10 ， 25k2 16 ∴|FA||FB||AB|10， ∴△FAB的周长为定值10． ………………………………………（12分）  x2  3 方法2：|AN| |OA|2 |ON|2  x2  y2 16  x2 161 1 16  x ， 1 1 1  25 5 1 3 同理|BN| x ， 5 2 3 ∴|AB| (x x )， 5 1 2  x2  又∵|AF| (x 3)2  y2  x2 6x 9161 1  1 1 1 1  25 9 3  2 3  x2 6x 25  x 5 5 x ， 25 1 1 5 1  5 1 3 同理|BF|5 x ， 5 2 ∴|FA||FB||AB|10， ∴△FAB的周长为定值10． ………………………………………（12分） 22．（本小题满分12分） alnxa alnx （1）解：函数 f(x) 的定义域为(0，)，求导得 f(x) ， x x2 若a0，则 f(x)0，无极值； 若a0，由 f(x)0得x1， 若a0， 数学参考答案·第8页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}当0x1时， f(x)0，则 f(x)单调递减；当x1时， f(x)0，则 f(x)单调递增， 此时，函数 f(x)有唯一极小值 f(1)a，无极大值； 若a0， 当0x1时， f(x)0，则 f(x)单调递增；当x1时， f(x)0，则 f(x)单调递减， 此时，函数 f(x)有唯一极大值 f(1)a，无极小值； 所以当a0时，函数 f(x)无极值； 当a0时，函数 f(x)有极小值 f(1)a，无极大值； 当a0时，函数 f(x)有极大值 f(1)a，无极小值． …………………………（6分） lnx 1 lnx 1 （2）证明：由(ex )x2 (ex )x1，两边取对数得x (lnx 1)x (lnx 1)，即 1  2 ， 1 2 2 1 1 2 x x 1 2 由（1）知，当a1时，函数 f(x)在(0，1)上单调递增，在(1，)上单调递减， 1 f(x)  f(1)1，而 f  0，x1时， f(x)0恒成立， max e 因此当a1时，存在x，x 且0x 1x ，满足 f(x ) f(x )， 1 2 1 2 1 2 若x [2，)，则x x x ≥2成立； 2 1 2 2 若x (1，2)，则2x (0，1)，记g(x) f(x) f(2x)，x(1，2)， 2 2 lnx ln(2x) lnx ln(2x) ln[(x1)2 1] 则g(x) f(x) f(2x)     0， x2 (2x)2 x2 x2 x2 即有函数g(x)在(1，2)上单调递增，所以g(x)g(1)0，即 f(x) f(2x)， 于是 f(x ) f(x ) f(2x )， 1 2 2 而x (1，2)，2x (0，1)，x (0，1)，函数 f(x)在(0，1)上单调递增， 2 2 1 因此x 2x ，即x x 2． ………………………………………（12分） 1 2 1 2 数学参考答案·第9页（共9页） {#{QQABaQCEggAAAgBAAAgCAQkiCEEQkAEAAKoOABAMMAAAARNABCA=}#}