云南师大附中2024届高考适应性月考卷（十）数学（云南版）-答案_2024年6月(1)_01按日期_01号_2024届云南师大附中高三适应性考试（十）

数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项符合题目要求） 题号 1 2 3 4 5 6 7 8 答案 C D B A D B C B 【解析】 1．依题意，M {x|(x5)(x3)≤0}{x|3≤x≤5}，N {y| y0}，故M N (0，5]， 故选C． 13(a a ) 132a 2．在等差数列{a }中，S  1 13  7 26，∴a 2．又∵a a a a 2a n 13 2 2 7 1 13 5 9 7 4，∴a a a a a 10，故选D． 1 5 7 9 13 2sincos2(2cos21)2 2sincos4cos2 2tan4 3．sin22cos22   sin2cos2 sin2cos2 tan21 2 2 4 3 24   ，故选B． 2 2 13   1 3 4．由PA2，则点P在圆A：(x3)2  y2 4上，又有点P在圆C上，所以需满足两圆有交点， 即1≤ (3a)2 (0a)2≤3，所以a[0，3]，故选A． 5．108023 33 5，1080的正因子可写为2k 3m 5n，其中k，m{0，1，2，3}，n{0，1}，故 1080的不同正因子共有44232个，故选D． 6．因为函数y f(x2)为奇函数，则 f(x2)f(x2)，即 f(2x) f(2x)0，可得 f(4x) f(x)0 . 又 因 为 f(1x) f(x1) ， 则 f(4x) f(x2) ， 所 以 ， f(x) f(x2)0，可得 f(x) f(x2)0，则 f(x2) f(x2)，即 f(x4) f(x)， 所以， f(2023) f(45053) f(3)1312，故选B．     7．方法一：点O是△ABC内心的充要条件是：aOAbOBcOC 0，其中BC a，AC b，  b  c  bc 1 a ABc，AO AB AC ，故  1 . 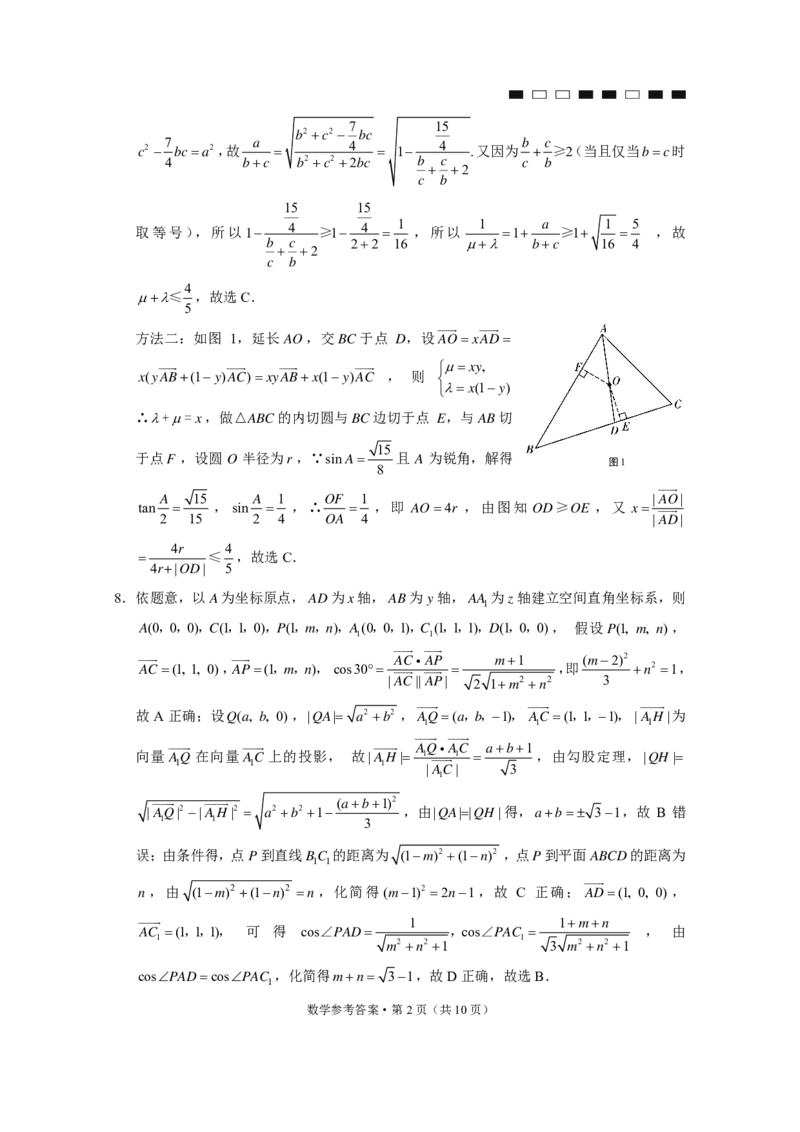因为角 abc abc abc  bc 15 7 b2 c2 a2 7 A为锐角，sinA ，所以cosA .由余弦定理得到cosA  b2  8 8 2bc 8 数学参考答案·第1页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}7 15 b2 c2  bc c2  7 bca2，故 a  4  1 4 .又因为 b  c ≥2（当且仅当bc时 4 bc b2 c2 2bc b c c b  2 c b 15 15 4 4 1 1 a 1 5 取等号），所以1 ≥1  ，所以 1 ≥1  ，故 b c 22 16  bc 16 4  2 c b 4 ≤ ，故选C． 5   方法二：如图 1，延长AO，交BC于点 D，设AOxAD     xy， x(yAB(1 y)AC)xyABx(1 y)AC ， 则  x(1 y) ∴+=x，做△ABC的内切圆与BC边切于点 E，与AB切 15 于点F ，设圆 O 半径为r ，∵sinA 且 A 为锐角，解得 图1 8  A 15 A 1 OF 1 |AO| tan  ， sin  ，∴  ，即 AO4r ，由图知 OD≥OE ，又 x  2 15 2 4 OA 4 |AD| 4r 4  ≤ ，故选C． 4r|OD| 5 8．依题意，以A为坐标原点，AD为x轴，AB为y轴，AA 为z轴建立空间直角坐标系，则 1 A(0，0，0)，C(1，1，0)，P(1，m，n)，A(0，0，1)，C (1，1，1)，D(1，0，0)， 假设P(1，m，n)， 1 1     AC AP m1 (m2)2 AC (1，1，0)，AP(1，m，n)，cos30    ，即 n2 1， |AC||AP| 2 1m2 n2 3    故A正确；设Q(a，b，0)，|QA| a2 b2 ，AQ(a，b，1)， AC (1，1，1)，|AH |为 1 1 1      AQ AC ab1 向量 AQ 在向量 AC 上的投影， 故|AH | 1 1  ，由勾股定理，|QH | 1 1 1 |AC| 3 1   (ab1)2 |AQ|2 |AH |2  a2 b2 1 ，由|QA||QH |得，ab 31，故 B 错 1 1 3 误；由条件得，点P到直线BC 的距离为 (1m)2 (1n)2 ，点P到平面ABCD的距离为 1 1  n ，由 (1m)2 (1n)2 n，化简得(m1)2 2n1，故 C 正确； AD(1，0，0) ，  1 1mn AC (1，1，1)， 可 得 cos∠PAD ，cos∠PAC  ， 由 1 1 m2 n2 1 3 m2 n2 1 cosPADcosPAC ，化简得mn 31，故D正确，故选B． 1 数学参考答案·第2页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有 多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分） 题号 9 10 11 答案 ACD ABD ACD 【解析】 13i (13i)(12i) 55i 9．(12i)z13iz  = 1i，则|z| (1)2 12  2 ，故A 12i (12i)(12i) 5 正确；z 的虚部为 1，故 B 错误；z 对应的点(1，1)在第二象限，故 C 正确；因为 (1i)2 2(1i)22i22i20，所以复数z是方程x2 2x20的一个根，故 D正确，故选ACD． π 10．由于函数 f(x) Acos(x)(0)是奇函数，所以kπ (kZ)，由于将y f(x)的 2 1 π 图象上各点的横坐标变为原来的 倍（纵坐标不变），再将图象向右平移 个单位长度， 2 6  π  得到yg(x)的图象，则g(x) Acos2x  ，对于A，因为曲线yg(x)的两条  3  π 2π 相邻对称轴之间的距离为 ，故T  π ，解得1，故 A 正确；所以函数 2 2  π   π f(x) Acosx kπ ，则 f(x) Asinx 或 f(x)Asinx ， g(x) Asin2x  或  2   3  π π π kπ 5π g(x)Asin2x  ，对于 B，令2x kπ (kZ)，解得x  (kZ)，所  3 3 2 2 12 5π π 以当k 0时，g(x)的图象关于直线x 对称，故B正确；对于C，令2x kπ(kZ)， 12 3 kπ π π  解得x + ，所以当k 0时，所以g(x)的图象关于点  ，0 对称，故C不正确；对 2 6 6  π  π 于 D ， 当 f  2 时 ， A2 或 A2， 所 以 g(x)2sin2x  ， g(x) 2  3  π  π  π π  π π 2sin2x  ，当g(x)2sin2x  ，x  0，  时，2x    ，  ，所以g(x)在  3  3  3 3  3 3  π π  π  π  0，  上单调递增，故函数的最大值为g  3；当g(x)2sin2x  ，x  0，   3 3  3  3 数学参考答案·第3页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}π  π π  π 时，2x   ， ，所以g(x)在 0， 上单调递减，故函数的最大值为g(0) 3，     3  3 3  3 故D正确，故选ABD． x2 y2 11．双曲线C ：  1中，实半轴长 a4 ，虚半轴长b3，半焦距 c5 ，焦点 16 9 3 F(5，0)，F (5，0)，对于 A，双曲线C的渐近线方程为y x，A 正确；对于 B，由 1 2 4 于点A，B在双曲线的右支上，设直线AB的倾斜角为，则由双曲线的第二定义可得： 72 9 |AB| ，∴当90时，|AB|  ，B 错误；对于 C，由双曲线定义知 1625cos2 min 2 |AF ||AF |8，而|FF |10，且 AF  AB，则|AF |2 |AF |2|FF |2100，即有 1 2 1 2 1 1 2 1 2 |AF ||AF | 2(|AF |2 |AF |2)(|AF ||AF |)2 2 34 ，因此|AF |4 34 ，C 正 1 2 1 2 1 2 1 确；对于D，由双曲线定义知|BF ||BF |8，因为AF  AB，设△ABF 内切圆的半径r ， 1 2 1 1 |AF ||AB||BF | |AF ||AF ||BF ||BF | 2 348 则由圆的切线性质知：r 1 1  1 2 2 1  2 2 2  344，D正确，故选ACD． 三、填空题（本大题共3小题，每小题5分，共15分） 题号 12 13 14 1 答案 乙 6；a≥3 2 【解析】 12．由图知：  ，所以乙的成绩更稳定. 1 2 1 1 13．∵a a a  ，∴a a a  ，∴两式作差得：a a ，∴数列{a }是以 n2 n1 n 2 n3 n2 n1 2 n n3 n 1 3 为周期的数列. 又∵a 1，a  ，∴a 1. 设数列{a }的前n项积为T ，则当 1 2 2 3 n n  1 k  1 k n3k，kN时，则T   ；则当n3k1，kN时，则T   ；则当 3k  2 3k1  2  1 k1 1 n3k2，kN时，则T   ，∴数列{a }的前n项积的最大值为 . 3k2  2 n 2 数学参考答案·第4页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}2 2 14．设直线y2xb与函数 f(x)2lnx的切点为(x，2lnx )，由 f(x) ，所以 f(x ) 0 0 x 0 x 0 2，解得x 1，所以切点为(1，0)，所以021b，解得b2，即切线方程为y2x2. 0 1 1 设 直 线 y2x2 与 函 数 g(x) ax2 x (a0) 的 切 点 为 (x，y ) ， 则 2 2 1 1 1 1  ax2 x  2x 2， x 1， 2 1 1 2 1 解得 1 即a3，所以ab6；设切线方程l为ykxm，  ax 12， a3， 1 1 1 且l与 f(x)2lnx的切点为(x，y )，l与g(x) ax2 x (a0)的切点为(x，y )，则 2 2 2 2 3 3 kx m2lnx， 1 1  2 2 kx m ax2 x  ， 2 1 (k1)2  2  3 2 3 3 2 整理可得m2ln 2，m  ， k  ， k 2 2a   x 2  k ax 3 1， 2 1 (k1)2 (k1)2 (x1)2 所以 2ln 2  ，整理可得 2a ，设 h(x) ，则 k 2 2a k 3 x 3 2ln  2ln  2 2 2 2  x 3 4 1  x 1 1 2(x1)2ln  (x1)2   2(x1)2ln     2 2 x 2  2 2 x x 1 h(x)  . 设 (x)2ln   x 3 2  x 3 2 2 2 2ln   2ln    2 2  2 2 1 2 1  ，则(x)  0，所以(x)在(0，)上为增函数，又因为(2)0，所以在 x x x2 (0，2)上(x)0，即h(x)0，所以h(x)单调递减； 在(2，)上(x)0，即h(x)0， 9 所以h(x)单调递增，所以h(x)≥h(x) h(2) 6，即2a≥6，解得a≥3. min 3 2 四、解答题（本大题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤） 15．（本小题满分13分） 解：（1）由题知：(0.0100.015m0.0350.010)101，解得m0.030. ………………………………………………………………（2分） (90x) 设x为样本数据的上四分位数，则： 10m0.10.25， 10 解得x85，故这组样本数据的上四分位数为85. …………………………（5分） 数学参考答案·第5页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}（2）设 p表示在这批产品中随机抽取一件产品，所抽取的产品为优秀品的概率， 由题知： p10(m0.01)0.4. …………………………………………（7分） 随机变量X B(5，0.4)，E(X)50.42， 随机变量X 的可能取值为：0，1，2，3，4，5， 243 810 162 P(X 0)C0p0(1 p)5  ，P(X 1)C1p1(1 p)4   ， 5 3125 5 3125 625 1080 216 720 144 P(X 2)C2p2(1 p)3   ，P(X 3)C3p3(1 p)2   ， 5 3125 625 5 3125 625 240 48 32 P(X 4)C4p4(1 p)1   ，P(X 5)C5p5(1 p)0  . 5 3125 625 5 3125 故随机变量X 的分布列为： X 0 1 2 3 4 5 243 162 216 144 48 32 P 3125 625 625 625 625 3125 …………………………………………………………（13分） 16．（本小题满分15分） 解：（1）由题意知，直线AB的斜率不为零，设直线AB的方程为：xmy4， 联立抛物线C：y2 2px(p0)的方程得：y2 2pmy8p0， 4p2m2 32p0恒成立， 设A(x，y )，B(x，y )，所以y  y 2pm，y  y 8p. 1 1 2 2 1 2 1 2   又OAOBxx  y y (my 4)(my 4) y y 0， 1 2 1 2 1 2 1 2 即(m2 1)y y 4m(y  y )160，所以168p0，即 p2， 1 2 1 2 所以抛物线C的方程为y2 4x. ………………………………（8分） （2）由（1）知：y2 4my160，y  y 4m，y  y 16， 1 2 1 2 所以|AF||BF|(x 1)(x 1)(my 5)(my 5) 1 2 1 2 m(y  y )104m2 10≥10， 1 2 当且仅当m0时取等号，所以|AF||BF|的最小值为10. ……………………（15分） 数学参考答案·第6页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}17．（本小题满分15分） 1 n 1 解：（1）∵S   ，∴当n1时，a S  ； n 3 1 1 3 1 n1 当n≥2时，S   ， n1 3 1 n1 1 n 2 ∴a S S      . n n n1 3 3 3n 2 ∵数列{a }是等比数列，∴a  对n1也成立， n n 3n 2 1 ∴  ，即1. ………………………………………………（6分） 3 3 2 （2）由（1）知：a  ， n 3n 2 ∴b 2log a 2log 2log 22n， n 3 n 33n 3 2 ∴令c a b  2n2log 2， ……………………………………（9分） n n n 3n 3 1 1 1 2 1 n ∴T 2      2(12n)n2log 2 n 3 3 3  3 1 1 n 1   3 3  n(1n) 2 2 2nlog 2 1 2 3 1 3 1 n n2 n  2nlog 21. ……………………………………（15分） 3 3 18．（本小题满分17分） （1）证明：如图2，取AE的中点M ，连接PM，BM ， AE 则由ADDE且APPE，可得PM  AE，且PM   2， 2 π 2 ∴由余弦定理可得MB2  AM2  AB2 2AM  ABcos 2162 24 10， 4 2 ∴PM2 MB2 PB2，∴PM MB. 由AEMBM ，AE，MB平面ABCE，可得PM 平面ABCE. 数学参考答案·第7页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}又BE平面ABCE，∴PM BE. 又AEBE， 由PM AE M ，PM，AE平面PAE， ∴BE平面PAE. 又PA平面PAE，∴PABE. 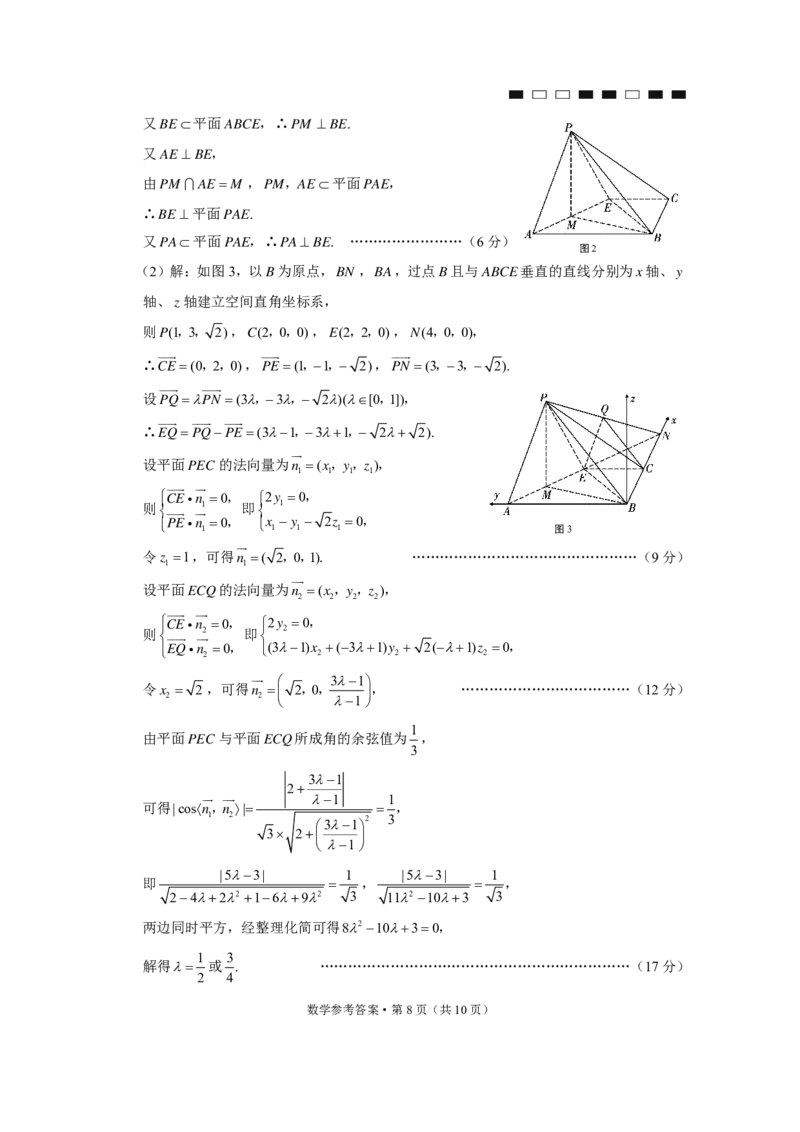……………………（6分） 图2 （2）解：如图3，以B为原点，BN ，BA，过点B且与ABCE垂直的直线分别为x轴、y 轴、z轴建立空间直角坐标系， 则P(1，3， 2)，C(2，0，0)，E(2，2，0)，N(4，0，0)，    ∴CE (0，2，0)，PE(1，1， 2)，PN (3，3， 2).   设PQPN (3，3， 2)([0，1])，    ∴EQPQPE(31，31， 2 2).  设平面PEC 的法向量为n (x，y，z )， 1 1 1 1    CEn 0，  2y 0， 则 1 即 1 PEn 1 0， x 1  y 1  2z 1 0， 图3  令z 1，可得n ( 2，0，1). …………………………………………（9分） 1 1  设平面ECQ的法向量为n (x，y，z )， 2 2 2 2    CEn 0，  2y 0， 则 2 即 2 EQn 2 0， (31)x 2 (31)y 2  2(1)z 2 0，   31 令x  2，可得n  2，0，  ， ………………………………（12分） 2 2  1  1 由平面PEC 与平面ECQ所成角的余弦值为 ， 3 31 2   1 1 可得|cosn，n |  ， 1 2 31 2 3 3 2   1  |53| 1 |53| 1 即  ，  ， 2422 1692 3 112 103 3 两边同时平方，经整理化简可得82 1030， 1 3 解得 或 . …………………………………………………………（17分） 2 4 数学参考答案·第8页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}19．（本小题满分17分） a ax （1）解：设R(x) 0 1 ， 1bx 1 ∵ f(0)ln10，∴R(0)a 0， 0 ax a (1bx)bax a 1 R(x) 1 ，R(x) 1 1 1 1  1 ， f(x) . 1bx (1bx)2 (1bx)2 1x 1 1 1 ∵ f(0)1，∴R(0)a 1， 1 1 2b 1 R(x) ，R(x) 1 ， f(x) . (1bx)2 (1bx)3 (1x)2 1 1 1 ∵ f(0)1，∴R(0)2b 1，∴b  ， 1 1 2 x 2x R(x)  . ……………………………………（4分） 1 2x 1 x 2 1 a x2 ax1 （2）①解：h(x)1   . x2 x x2 a 当a≤0时，令g(x)x2 ax1，g(0)1，对称轴 ≤0，x0，g(x)0恒成立， 2 ∴h(x)在(0，)； ………………………………………………………………（6分） 当0a≤2时，a2 4≤0，h(x)≥0，h(x)在(0，)上单调递增； ………………………………………………………………（8分） a a2 4 a a2 4 当 a2 时， a2 40 ，令 h(x)0 ，解得 m ， n ，且 2 2 0mn，  a a2 4 a a2 4 a a2 4 ∴h(x)在0， 上单调递增，在 ， 上单调递减，在  2   2 2      a a2 4   ，上单调递增. ……………………………………（10分）  2    ②证明：x0，h(x)，x，h(x). 当a≤2时，h(x)在(0，)上单调递增，则存在唯一零点，不合题意； 当a2时，h(1)2a0，所以0m1n， 1 1  1  极大值h(m)m alnmm m lnm， m m  m 数学参考答案·第9页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}m2 1 欲证h(m)0，可证 lnm0. m2 1 m2 1 令g(m) lnm，m(0，1)， m2 1 4m 1 (m2 1)2 则g(m)   0， (m2 1)2 m m(m2 1)2 ∴g(m)在(0，1)上单调递减，g(m)g(1)0，即h(m)0， 同理可得，极小值h(n)0. 由零点存在性定理，h(x)有3个不同零点x，x，x ，且0x x 1x， 1 2 3 1 2 3 要证：x x x 2a1，即证x x 2(a1). 1 2 3 1 3 2(x1) 由（1）得，当x1时，lnx . x1 2(x1) 下证：x1时，lnx ， x1 令(x)(x1)lnx2(x1)，x1， x1 1 1 1 (x)lnx 2lnx 1，(x)  0， x x x x2 ∴(x)(1)0，所以(x)(1)0. 1 2a(x 1) 由h(x )0，x  alnx  3 ， 3 3 x 3 x 1 3 3 x2 1 2a(x 1) 1 即 3  3 ，(x 1)2 2ax ，x  2a2， x x 1 3 3 3 x 3 3 3  1  1 1 又有h  x aln h(x )0h(x )， x  x 3 x 3 1 3 3 3 1 所以 x ，故x x 2(a1). ………………………………（17分） x 1 1 3 3 数学参考答案·第10页（共10页） {#{QQABbQAEggAoQIBAAQhCEwUCCgEQkBAAASgGABAAsAABwANABAA=}#}