云南师大附中2024届高考适应性月考卷（三）数学（云南版）-答案_2023年9月_01每日更新_26号_2024届云南师范大学附属中学高考适应性月考卷（三）

数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项符合题目要求） 题号 1 2 3 4 5 6 7 8 答案 C B D C A D C C 【解析】 43i (43i)(12i) 211i 2 11  2 11 1．z     i，则z在复平面内对应的点为  ，  ， 12i (12i)(12i) 5 5 5  5 5  位于第三象限，故选C． 2．由图可知AB，对于A，xA，xB正确；对于B，x(AB)，xB不正确； 对于C，xA，xB正确；对于D，x(AB)，xU 正确，故选B． 1 3．对于 A， y 的定义域为(0，)，为非奇非偶函数，故 A 错误；对于 B，设 x ex ex ex ex ex ex y f(x) ，则 f(x)  f(x)，故函数y f(x) 为偶函数，故B 2 2 2  π  错误；对于C，设yh(x)tanx，其定义域为 x x kπ，kZ ，在定义域内不是减  2  ex ex ex ex 函数，故C错误；对于D，设yg(x) ，定义域为R，且g(x) g(x)， 2 2 ex ex 故 yg(x) 为 奇 函 数 ， 又 yex 与 yex 在 R 上 都 为 减 函 数 ， 故 2 ex ex yg(x) 在R上为减函数，故D正确，故选D． 2 4．根据题意，分 2 种情况讨论：①4 位“回文数”中数字全部相同，有 9 种情况，即此时有 9个4位“回文数”；②4位“回文数”中有2个不同的数字，有A2 72种情况，即此时 9 有72个4位“回文数”，则一共有97281个4位“回文数”，故选C． sin35 sin55 sin35cos55cos35sin55 sin(5535) 2sin20 5．tan35tan55     cos35 cos55 cos35cos55 cos35sin35 sin70 2sin20  2tan20，所以2tan20+tan35tan550，故选A． cos20 数学参考答案·第1页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}lnx 6．函数 f(x)lnxax在(0，2e)上有两个不同的零点等价于曲线y  和y a在(0，2e) 1 x 2 lnx 1lnx 上有两个不同的交点，设g(x) ，g(x) ，令g(x)0，解得xe，所以g(x) x x2 1 ln2e 在(0，e)上单调递增，在(e，2e)上单调递减， g(e) ， g(2e) ，且 x0时， e 2e ln2e 1 g(x)，故a的取值范围为  ，  ，故选D．  2e e 7．由等比数列前n项和的性质可得S ，S S ，S S ，S S 成等比数列，所以有 6 12 6 18 12 24 18 (S S )2 S (S S )，即(S 10)2 10(70S )，整理可得S2 10S 6000，解 12 6 6 18 12 12 12 12 12 得 S 20 （ 舍 ） 或 S 30 ， 又 因 为 (S S )2 (S S )(S S ) ， 所 以 有 12 12 18 12 12 6 24 18 (7030)2 (3010)(S 70)，解得S 150，故选C． 24 24 8．双曲线C的左焦点F(c，0)，渐近线l 的方程为bxay0，由点到直线的距离公式可得 1 1 bc bc |MF |  b ，由勾股定理得|OM | |OF |2 |MF |2  c2 b2 a ，在 1 b2 (a)2 c 1 1 π |OM | a Rt△MOF 中，OMF  ，所以cosMOF   ，在△MOF 中，|OM |a ， 1 1 2 1 |OF | c 2 1 a |MF |3a，|OF |c，cosMOF cos(πMOF)cosMOF  ，由余弦定理得 2 2 2 1 1 c |OM |2 |OF |2 |MF |2 a2 c2 9a2 a cosMOF  2 2   ，化简得c2 6a2，即c 6a， 2 2|OM ||OF | 2ac c 2 c 因此，双曲线C的离心率为e  6 ，故选C． a 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有 多项符合题目要求，全部选对的得5分，选对但不全的得2分，有选错的得0分） 题号 9 10 11 12 答案 AB BCD ACD CD 【解析】 42 2 9．对于A，由CD2AB2AD2BC 4cm，可得高OO  4   3，则圆台轴 1 2  2  1 截面 ABCD的面积为 (24) 33 3cm2，故 A 正确；对于 B，圆台的侧面积为 2 数学参考答案·第2页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}S π(12)26π(cm2) ， 又 S π12 π(cm2) ， S π22 4π(cm2) ， 所 以 侧 上 下 1 S 6ππ4π11π(cm2)，故 B 正确；对于 C，圆台的体积为V  π 3(142) 表 3 7 3  π(cm3)，故C错误；对于D，若圆台存在内切球，则必有轴截面ABCD存在内切圆， 3 由内切圆的性质以及切线长定理易知轴截面ABCD不存在内切圆，故D错误，故选AB．  p   p 10．对于A，因为F ，0 ，直线的斜率为 3，则设直线l的方程为y 3x  ，联立  2   2 y2 2px，  3p p p   p 得12x2 20px3p2 0 ，解得： x  ，x  ，由|AF|x   y 3x  ， A 2 B 6 A 2   2 p 2 2p4，得 p2，故A错误；对于B，由于|BF|x   p，则|AF|3|BF|，故 B 2 3 B正确；对于C，抛物线C：y2 4x的焦点为F(1，0)，|ED||EE ||ED||EF|≥|DF| 1  2，当且仅当D，E，F三点共线时取等号，故C正确；对于D，当直线斜率不存在时， 直线方程为x0，与抛物线只有一个公共点；当直线斜率存在时，设直线方程为ykx1， ykx1， 联立 消x得ky2 4y40，当k 0时，方程的解为y1，此时直线与抛物 y2 4x， 线只有一个交点；当k 0时，则1616k 0，解得k 1，综上所述，过点D与C有 且仅有一个公共点的直线有3条，故D正确，故选BCD． 11．对于A，从6天内的发芽率来看，甲类种子为60%，乙类种子为70%60%，故A正确； 对于 B，若种下 16 粒甲类种子，由题意可知发芽数 X 服从二项分布，X B(16，0.6)， E(X)9.6，P(X 9)C9 0.69(10.6)169 C9 0.690.47 ，P(X 10)C100.610(10.6)1610 16 16 16 P(X 9) C9 0.69 0.47 10 1 20 C100.6100.46，而  16   0.4 1，所以 10 粒种子 6 16 P(X 10) C10 0.610 0.46 7 0.6 21 16 天内发芽的概率更大，故B错误；对于C，记事件A：样本甲种子中随机取一粒10天内 发芽；事件 B：样本乙种子中随机取一粒 10 天内发芽；根据对立事件的性质，这两粒种 子至少有一粒 10 天内未发芽的概率为：1P(AB)1P(A)P(B)10.90.95 10.8550.145，故C正确；对于D，由题意可知X服从二项分布，X B(1600，0.25)， 所以E(X)16000.25400，D(X)16000.25(10.25)300，故D选项正确，故选 ACD． 数学参考答案·第3页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}1 12．令 f(x)ex  x2 cosx，则 f(x)ex xsinx，令g(x)ex xsinx，g(x)ex 1 2 cosx，当x0时，g(x)ex sinx0，g(x)单调递增，g(x)g(0)10，故g(x) 在(0，)上单调递增；因为g(x)g(0)10，即 f(x)0在(0，)上恒成立， f(x) 1 1 1 在(0，)上单调递增且 f(x) f(0)0，即ex  x2 cosx，从而ex  y2 cosy x2 2 2 2 1 cosx，令(x) x2 cosx(x0)，(x)xsinx0(x0)，则(x)在(0，)上单 2 调递增，则yx，故选CD． 三、填空题（本大题共4小题，每小题5分，共20分） 题号 13 14 15 16 3  答案 13 5  ，1  0 4  【解析】             13．由题意知，|a|2，|b|1，ab|a||b|cos601，因为(2ab)2 4a2 b2 4ab     161413，所以|2ab| (2ab)2  13． 14．设圆锥的顶点为S，底面圆心为O，过圆锥顶点S的平面截圆锥所得截面为SAB，E为AB 1 的中点，则OE  AB，由tanSAO ，得OA3SO，因为圆锥母线长为 10，结合勾 3 股定理解得 OA3 ， SO1 ， AB2 OA2 OE2 2 9OE2 ， SE  SO2 OE2 1 1  1OE2 ， 所 以 S  ABSE  2 9OE2  1OE2  (9OE2)(1OE2) △SAB 2 2  (OE2 4)2 25，因为0≤OEOA3，0≤OE2 9，所以当OE2 4，OE2时， S 取得最大值为5． △SAB 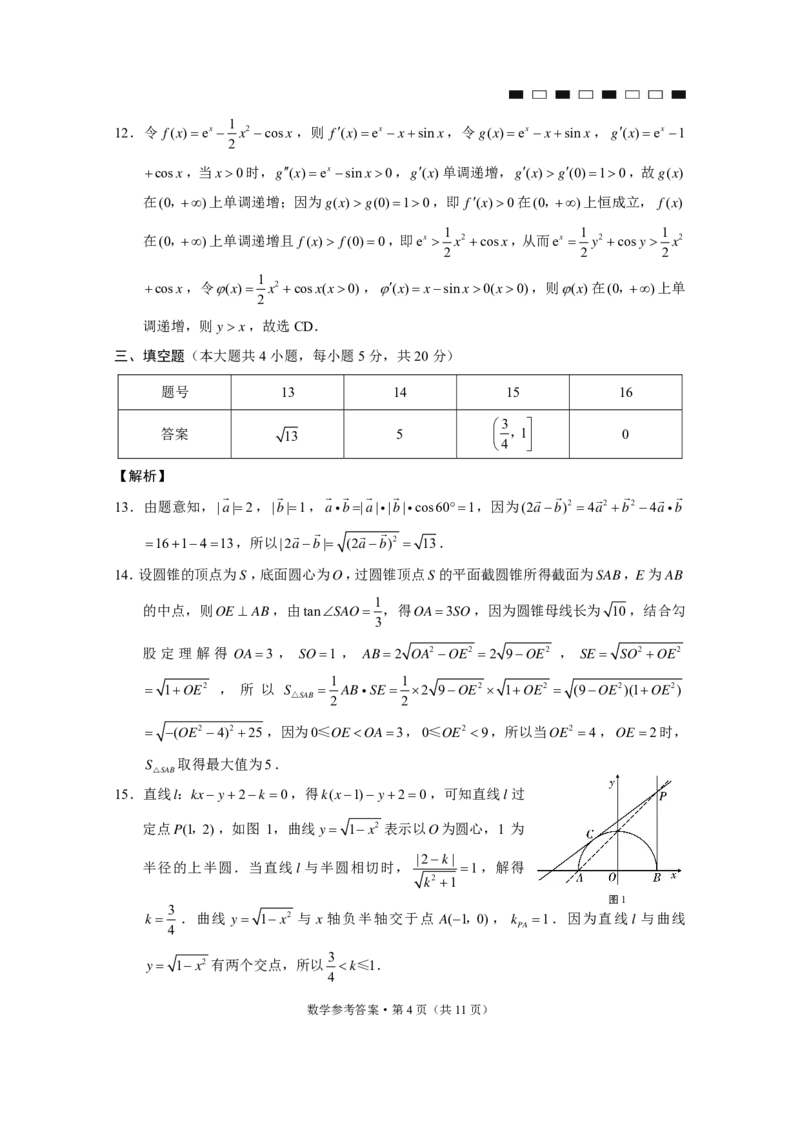15．直线l：kx y2k 0，得k(x1) y20，可知直线l过 定点P(1，2)，如图 1，曲线y 1x2 表示以O为圆心，1 为 |2k| 半径的上半圆．当直线l 与半圆相切时， 1，解得 k2 1 图1 3 k  ．曲线 y 1x2 与 x 轴负半轴交于点 A(1，0)，k 1．因为直线l 与曲线 4 PA 3 y 1x2 有两个交点，所以 k≤1． 4 数学参考答案·第4页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}3π 3π π 3π π π 16．由题图可知A2，因为 f  1，所以2sin  1，   2kπ，kZ，  2   2 3 2 3 6 1 4k 3π 23π 29π 2π 3π 23π 29π 解得  ，kZ. 又T    ，即    且0，所以 3 3 2 25 50  2 25 50 100 1 5 1 1 π 0 ，所以 或3或 ；当 时，f(π)2sin π 0，由图 29 3 3 3 3 3  π 象 知 不 符 合 题 意 ， 当 3 时 ， f(x)2sin3x  ， 此 时  3 23π  23π π 182π 5 f  2sin3  2sin 0 ， 不 符 合 题 意 ， 当  时 ，  25   25 3 75 3 5 π 23π 5 23π π 6π f(x)2sin x  ，此时 f  2sin   2sin 0，符合题意，所以 3 3  25  3 25 3 5 5 π f(5π)2sin 5π 2sin8π0． 3 3 四、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分10分） abc b 解：（1）由  整理可得bcb2 c2 a2， …………………（1分） c abc b2 c2 a2 bc 1 由余弦定理可得cosA   ， …………………………………（3分） 2bc 2bc 2 又0 Aπ， …………………………………………………………（4分） π 所以A ． …………………………………………………………（5分） 3 1 1 cosB cosC sinCcosBsinBcosC sin(BC) （2）      tanB tanC sinB sinC sinBsinC sinBsinC sinA 3   ， …………………………………………（7分） sinBsinC 2sinBsinC π 2π 由A ，可得C  B. 3 3 因为△ABC为锐角三角形，  π 0B ，   2 π π 所以 解得 B ， ………………………………………（8分） 2π π 6 2 0 B ，  3 2 数学参考答案·第5页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}2π   3 1  3 1 1 所以sinBsinC sinBsin BsinB  cosB sinB   sin2B cos2B  3   2 2  4 4 4 1  π 1  sin2B  . ……………………………………………………（9分） 2  6 4 π π 5π 因为 2B  ， 6 6 6 1  π 1 1  π 1 3 1 3 所以 sin2B  ≤1，  sin2B  ≤ ，即 sinBsinC≤ ， 2  6 2 2  6 4 4 2 4 1 1 2 3  则   ， 3． …………………………………………（10分）  tanB tanC 3   18．（本小题满分12分） 解：（1）由表格知：x2020，y2.00， ………………………………（2分） 5 所以(x x)2 (2)2 (1)2 012 22 10， ………………………………（3分） i i1 5 (y  y)2 (0.4)2 (0.3)2 (0.1)2 (0.2)2 (0.6)2 0.66， …………………（4分） i i1 5 (x x)(y  y)(2)(0.4)(1)(0.3)010.220.62.5， i i i1 …………………………………………………………………（5分） 5 (x x)(y  y) i i 2.5 2.5 由上，有r i1   0.960.75， 5 5 10  0.66 2.6 (x x)2  (y  y)2 i i i1 i1 所以y与x之间的线性相关性较强． ……………………（6分） （2）依题意，完善表格如下： 购置传统燃油车 购置新能源车 总计 男性车主 35 25 60 女性车主 15 25 40 总计 50 50 100 ……………………………………………………………………（8分） 数学参考答案·第6页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}100(35251525)2 25 则2的观测值2   4.173.841， ………………（11分） 50504060 6 根据小概率值0.05的独立性检验，我们认为购车车主购置新能源乘用车与性别是有 关，此推断犯错误概率不大于0.05． ……………………………………………（12分） 19．（本小题满分12分） （1）解：设等差数列{a }的公差为d，等比数列{b }的公比为q， n n 由a 1，a 5(a a )，可得14d 5d ， …………………………………（1分） 1 5 4 3 解得d 1， ………………………………………………………………（2分） 所以{a }的通项公式为a n； …………………………………………（3分） n n 因为b 2，b 4(b b )， 1 5 4 3 所以q4 4(q3 q2)， ……………………………………………………（4分） 因为q0，所以q2 4q40，解得q2， ………………………（5分） 从而{b }的通项公式为b 2n． …………………………………………（6分） n n 1 1 11 1  （2）证明：由（1）可得，n为奇数时，c       ， n a a n(n2) 2n n2 n n2 n为偶数时，c b 2n， …………………………………………（7分） n n 2n 设T c c c c c c c 2n i 1 2 3 4 2n1 2n i1 (c c c c )(c c c c ) …………………………（8分） 1 3 5 2n1 2 4 6 2n 1 1 1 1 1 1 1 1   1       (22 24 26 22n) 2 3 3 5 5 7 2n1 2n1 ……………………………………………………………（9分） 1 1  4(14n)  1  2 2n1 14 n 4n1 4    …………………………………………（10分） 2n1 3 3 1 4n1 5    ， …………………………………………（11分） 4n2 3 6 所以T 关于n(nN*)单调递增， 2n 2n 13 则T c≥T  ． …………………………………………（12分） 2n i 2 3 i1 数学参考答案·第7页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}20．（本小题满分12分） （1）证明：在三棱柱ABCABC 中， 1 1 1 因为△ABC为正三角形，D是BC的中点， …………………………（1分） 所以ADBC. ………………………………………………（2分） 因为平面BBCC 平面ABC，平面BBCC平面ABC BC，AD平面ABC， 1 1 1 1 …………………………………………………………………（3分） 所以AD平面BBCC. ……………………………………………………（4分） 1 1 因为BB 平面BBCC， 1 1 1 所以ADBB ． ………………………………………………………………（5分） 1 （2）解：由题意知△BBC 为正三角形，连接BD， 1 1 则BDBC. 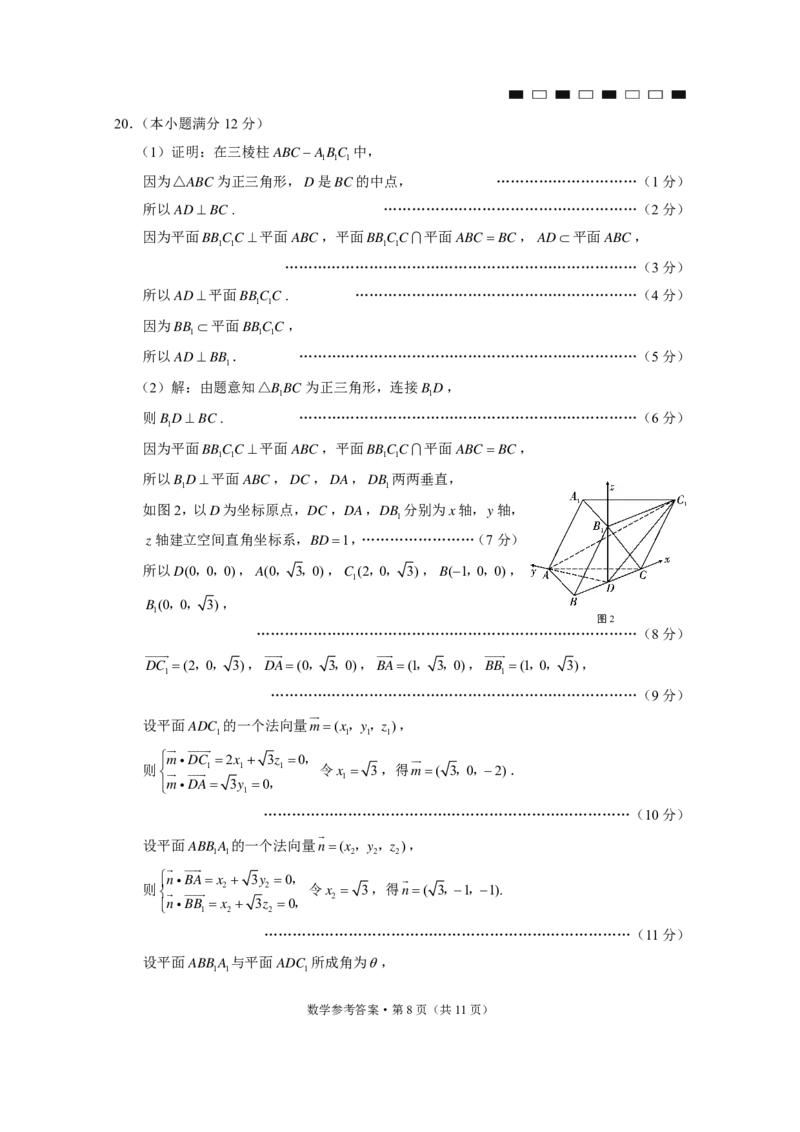………………………………………………………………（6分） 1 因为平面BBCC 平面ABC，平面BBCC平面ABC BC， 1 1 1 1 所以BD平面ABC，DC，DA，DB 两两垂直， 1 1 如图2，以D为坐标原点，DC，DA，DB 分别为x轴，y轴， 1 z轴建立空间直角坐标系，BD1，……………………（7分） 所以D(0，0，0)，A(0， 3，0)，C (2，0， 3)，B(1，0，0)， 1 B(0，0， 3)， 1 图2 ………………………………………………………………………（8分）     DC (2，0， 3)，DA(0， 3，0)，BA(1， 3，0)，BB (1，0， 3)， 1 1 ……………………………………………………………………（9分）  设平面ADC 的一个法向量m(x，y，z )， 1 1 1 1    mDC 2x  3z 0，  则 1 1 1 令x  3，得m( 3，0，2)． 1 mDA 3y 0， 1 ……………………………………………………………………（10分）  设平面ABBA的一个法向量n(x，y，z )， 1 1 2 2 2    nBAx  3y 0，  则  2 2 令x  3，得n( 3，1，1). 2 nBB x  3z 0， 1 2 2 ……………………………………………………………………（11分） 设平面ABB A与平面ADC 所成角为， 1 1 1 数学参考答案·第8页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}    |mn| 35  35 2 14 则|cosm，n|    ，所以sin 1   ，   |m||n| 7  7  7 14 所以平面ABB A与平面ADC 所成角的正弦值为 ． ………………………（12分） 1 1 1 7 21．（本小题满分12分）  3 x2 y2 解：（1）由题意得a2，把 1，  代入  1， ………………………（1分）  2 4 b2 解得b 3， …………………………………………………………（3分） x2 y2 所以C的方程为  1． …………………………………………（4分） 4 3 （2）由（1）知：c a2 b2 1，F(1，0)， S |AF| 1 ①当l斜率不存在时，易知 △AEF   ； ………………………（5分） S |BF| 3 △BDF ②当l斜率存在时，设l：xty1(t 0)，D(x，y )(y 0)，E(x，y )(y 0)， 1 1 1 2 2 2 xty1，  由x2 y2 得(3t2 4)y2 6ty90，显然0， ……………………（6分）   1，  4 3 6t 9 所以y  y  ，y y  . …………………………………………（7分） 1 2 3t2 4 1 2 3t2 4 1 1 1 3 因为S  |AF|| y | (y )，S  |BF|| y |  y ， △AEF 2 2 2 2 △BDF 2 1 2 1 1 (y ) S 2 2 1 y 所以 △AEF    2 . …………………………………………（8分） S 3 3 y △BDF  y 1 2 1 36t2 (y  y )2 (3t2 4)2 4t2 4 4 因为 1 2     ， ………………………（9分） y y 9 3t2 4 4 3 1 2  3 3t2 4 t2 4 (y  y )2 所以  1 2 0. 3 y y 1 2 (y  y )2 y2 2y y  y2 y y 又 1 2  1 1 2 2  1  2 2， ………………………………（10分） y y y y y y 1 2 1 2 2 1 y 4 1 1 设 2 k ，则k 0， k 20，解得3k  且k 1， y 3 k 3 1 ……………………………………………………………………（11分） 数学参考答案·第9页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}S 1 y 1 1 1  所以 △AEF   2  ，    ，1. S 3 y 9 3 3  △BDF 1 1 1  因为  ，1 ， 3 9  S 1  综上， △AEF 的取值范围为  ，1 ． …………………………………………（12分） S 9  △BDF 22．（本小题满分12分） π 证明：（1）①当 xπ时，由于y2sinx单调递减，yln(1x)单调递减， 2 所以 f(x)单调递减. …………………………………………（1分） π  π 又 f  2ln1 0， f(π)ln(1π)0， 2  2 π  所以存在x  ，π ，使得 f(x )0， 0 2  0 π  即 f(x)在  ，π 只有1个零点，无极值点； …………………………（2分） 2  π 1 ②当0x 时， f(x)2cosx ， 2 x1 1 1 令g(x)2cosx ，g(x)2sinx ， x1 (x1)2 …………………………………………………………………………（3分） 1  π 因为y2sinx和y 在 0，  上均单调递减，所以g(x)单调递减. (x1)2  2 π 1 因为g(0)10，g  2 0， 2 π  2  1 2   π 所以存在x 0，  ，使得g(x )0. ………………………………………（4分） 1  2 1 π 当0xx 时，g(x)0，g(x)单调递增；当x x 时，g(x)0，g(x)单调递减； 1 1 2 π π 1 π π 1 又g  f  1 0，g  f   0， 3 3 π 2 2 π 1 1 3 2 π π 所以存在x  ，  ，使得g(x ) f(x )0. ………………………（5分） 2 3 2 2 2 数学参考答案·第10页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}因为g(0) f(0)10，所以当0xx 时， f(x)0， f(x)单调递增； 2 π 当x x 时， f(x)0， f(x)单调递减； 2 2 所以x 是 f(x)的极大值点. 2 π  π 因为 f(0)0， f  2ln1 0， 2  2 π 所以当0x 时， f(x)0恒成立，即函数 f(x)无零点； 2 综上，函数 f(x)有唯一的极值点m(mx )及唯一的零点n(nx )． 2 0 …………………………………………………………（6分） π π π  （2）由（1）知m ，  ，2m，n ，π ， 3 2 2  1 1 由于m为 f(x)的极值点，所以 f(m)2cosm 0，即2cosm ， m1 1m …………………………………………………………………（7分） 2sinm 所以 f(2m)2sin2mln(12m)4sinmcosmln(12m) ln(12m). 1m  π 设yxsinx0x  ，则y1cosx0，所以yxsinx单调递增，  2 所以xsinx0，即xsinx， …………………………………………（8分） 2sinm 2m 所以 f(2m) ln(12m) ln(12m). …………………（9分） 1m 1m 2x  π 2x2 令(x) ln(12x)0x  ，则(x) 0， 1x  2 (1x)2(12x) …………………………………………………………………（10分）  π 所以(x)在 0，  上单调递减，所以(x)(0)0，  2 所以 f(2m)0 f(n). ………………………………………………（11分） π  又因为 f(x)在  ，π 上递减，所以2mn． ……………………………（12分） 2  数学参考答案·第11页（共11页） {#{QQABZQSEogioAAIAAQhCUQFCCAMQkAAACKoGwFAIoAAAQAFABCA=}#}