文档内容
湘 豫 名 校 联 考
#$#%年&月高三秋季入学摸底考试
数学参考答案
题号 ! # % ’ ( ) * & " !$ !! !#
答案 + , - . . , , . .+, -., -+ -.,
一!选择题"本题共&小题#每小题(分#共’$分/在每小题给出的四个选项中#只有
一项是符合题目要求的/
!!+!$命题意图%本题考查集合的运算#解一元二次不等式及对数函数的定义域$考查了数学运算的核心素养!
$解析%因为集合"0!#"##1#1)#$"0#1#$%%$$0!#"%023##4!%"0#1!$45%$所以$! $0#15$
1!&!所以"%#$! $%0#1#$1!&!故选+!
#!,!$命题意图%本题考查复数的乘#除法运算及复数的相关概念$考查了数学运算的核心素养!!!
$解析%由题可得&0 #16 0 ##16%#!16% 0 !1%6 0 ! 1 % 6$则&10 ! 4 % 6$所以&1的虚部为 % !故选,!
!46 #!46%#!16% # # # # # #
%!-!$命题意图%本题考查直线与圆的位置关系$考查了数学运算#直观想象的核心素养!
"#槡#1#1!%4("
$解析%依题知圆心’#!$1!%$半径为%$则 0%$解得(0&1#槡#或(01!$1#槡#!故选-/
槡##槡#%#4#1!%#
’!.!$命题意图%本题考查三角函数的定义#正切的和角公式#诱导公式$考查了数学运算的核心素养!
%
4)
$解析%设783!0)$由题可得783"0
%
$所以783#"4! %0
783"4783!
0
’
0#$解得)0
!
!所以
’ !1783"783! % #
!1 )
’
!
783#%!1! %01783!01 !故选.!
#
(!.!$命题意图%本题考查向量的几何意义#向量的数量积运算#向量的夹角$考查了数学运算#逻辑推理的核
心素养!
’"!’""
0槡#$
""" "!"
$解析%由题可得& 所以 0槡##因为#!4"%)##!1%"%$所以#!4"%’##!1%"%0$$所以
"!’"" """
0!$
( "!"
"!"# "!" 槡#
#"!"#1%"""#1"!""""9:;(!$")0$$所以# 1%1 9:;(!$")0$$即9:;(!$")0 #所以(!$")0’(8?
00#!%0#!4!%#1!0%$0##%
>63
00#1!%0#1!4!%#1
!01!$所以"0##
#
%10##
!
%">8? 00##%
>8?
10##%
>63
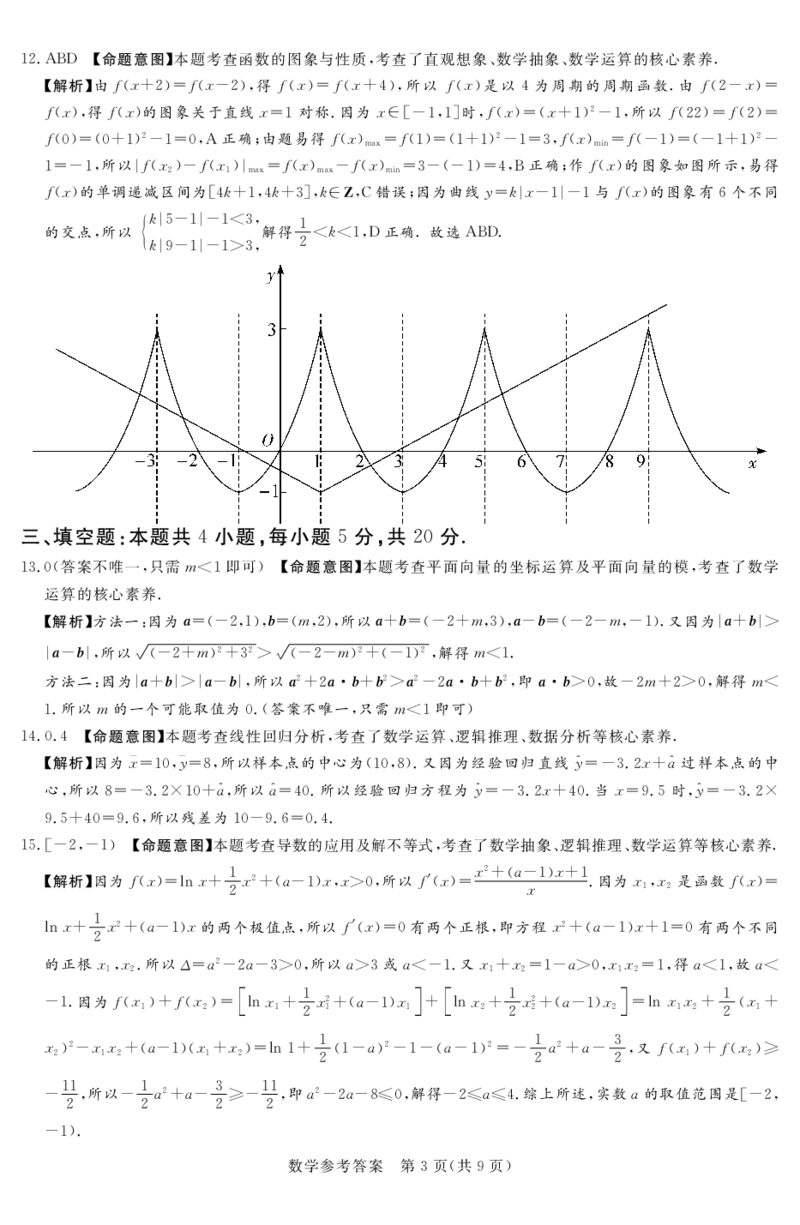
0%1#1!%0’$.正确*作0##%的图象如图所示$易得
0##%的单调递减区间为,’:4!$’:4%&$:/"$+错误*因为曲线%0:"#1!"1!与0##%的图象有)个不同
%:"(1!"1!#%$
!
的交点$所以 解得 #:#!$,正确/故选-.,/
:""1!"1!-%$ #
三!填空题"本题共’小题#每小题(分#共#$分!
!%!$!答案不唯一$只需3#!即可"!$命题意图%本题考查平面向量的坐标运算及平面向量的模$考查了数学
运算的核心素养!
$解析%方法一-因为!0#1#$!%$"0#3$#%$所以!4"0#1#43$%%$!1"0#1#13$1!%!又因为"!4""-
"!1""$所以槡#1#43%#4%#-槡#1#13%#4#1!%#$解得3#!!
方法二-因为"!4""-"!1""$所以!#4#!’"4"#-!#1#!’"4"#$即!’"-$$故1#34#-$$解得3#
!!所以3的一个可能取值为$!#答案不唯一$只需3#!即可%
!’!$!’!$命题意图%本题考查线性回归分析$考查了数学运算#逻辑推理#数据分析等核心素养!
$解析%因为#10!$$% 10&$所以样本点的中心为#!$$&%!又因为经验回归直线; %01%!##4;4过样本点的中
心$所以&01%!#=!$4;4$所以;40’$!所以经验回归方程为; %01%!##4’$!当#0"!(时$; %01%!#=
"!(4’$0"!)$所以残差为!$1"!)0$!’!
!(!,1#$1!%!$命题意图%本题考查导数的应用及解不等式$考查了数学抽象#逻辑推理#数学运算等核心素养!
! ##4#41!%#4!
$解析%因为0##%023#4
#
##4#41!%#$#-$$所以0<##%0
#
!因为#
!
$#
#
是函数0##%0
!
23#4 ##4#41!%#的两个极值点$所以0<##%0$有两个正根$即方程##4#41!%#4!0$有两个不同
#
的正根#
!
$#
#
!所以#04#1#41%-$$所以4-%或4#1!!又#
!
4#
#
0!14-$$#
!
#
#
0!$得4#!$故4#
& ! ’ & ! ’ !
1!!因为0##
!
%40##
#
%0 23#
!
4
#
##
!
4#41!%#
!
4 23#
#
4
#
##
#
4#41!%#
#
023#
!
#
#
4
#
##
!
4
! ! %
#
#
%#1#
!
#
#
4#41!%##
!
4#
#
%023!4
#
#!14%#1!1#41!%#01
#
4#441
#
$又0##
!
%40##
#
%0
!! ! % !!
1 $所以1 4#441 01 $即4#1#41&1$$解得1#141’!综上所述$实数4的取值范围是,1#$
# # # #
1!%!
数学参考答案!第!!!!%页!共"页"
{#{QQABCQqEoggAQABAABhCQQGwCgKQkBGCCIgOAAAEsAIASBFABAA=}#}#*
!)! !$命题意图%本题考查空间几何体的外接球及空间几何体的体积$考查了数学运算#直观想象#逻辑推理
&
等核心素养!
$解析%如图所示$点=是三棱锥. "$’外接球的球心$设球=的半径为>$= 是
!
*"$’外接圆的圆心$设圆=
!
的半径为?$点.到底面"$’的距离为@$由题意$
!(
可得’!>#0!(!$则>#0 !因为*"$’是边长为%的正三角形$所以由正弦定理$
’
$’ % !
可得#?0 0 $则?0槡%!所以三棱锥. "$’的体积为A0 7 @0
;63" ;63)$< % *"$’
! 槡% %槡%
= =%#=@0 @$三棱锥. "$’的体积取最大值则需要@最大!由题意可
% ’ ’
知$点.在过"$且与底面"$’#此处底面"$’为水平%垂直的截面圆的圆周上运动$当点.运动到该圆
的最高点时$@最大!如图所示$取"$的中点*$连接’*$.*$==
!
$.=$’=$过点=作=B).*!由圆的对
称性可知$此时."0.$$则.*)"$!又平面."$)平面"$’$且平面."$%平面"$’0"$$.*2平面
."$$所以.*)平面"$’!因为在*==
!
’中$=
!
=#4=
!
’#0=’#$又=
!
’0?0槡%$所以=
!
=#0=’#1
% 槡% ! 槡%
=’#0>#1?#0 !易得四边形==*B为矩形$所以B*0==0 $B=0=*0 ’*0 !因为在
! ’ ! ! # ! % #
%槡% #*
*.=B中$.B0槡.=#1=B#0槡>#1=B#0槡%$所以@
>8?
0.*0.B4B*0
#
$所以A
>8?
0
&
!
四!解答题"共*$分!解答应写出必要的文字说明!证明过程或演算步骤!
!*!$命题意图%本题考查三角函数的恒等变换#解三角形$考查了数学运算#数学建模的核心素养!!!
# # #
$解析%#!%因为0##%0#;63 9:; 4#槡%9:;# 1槡%0;63#4槡%#9:;#4!%1槡%
# # #
! !"
0;63#4槡%9:;#0#;63#4 $………………………………………………………………………… #分
%
! !" 槡%
又0#"%0槡%$所以;63"4 0 !
% #
!
因为"/#$$!%$所以"0 ! ……………………………………………………………………………… (分
%
4 4
##%由正弦定理得 0#槡%$即 0#槡%$
;63" !
;63
%
槡%
所以40#槡%= 0%!
#
!
由余弦定理得"0(#4C#1#(C9:; 0(#4C#1(C0#(C1(C0(C$当且仅当(0C时$等号成立!
%
所以(C1"!…………………………………………………………………………………………………… &分
! ! 槡%
因为7 0 ’(C’;63 0 (C$
*"$’ # % ’
又(C的最大值为"$
"槡%
所以*"$’面积的最大值为 !………………………………………………………………………… !$分
’
!&!$命题意图%本题考查二项分布#互斥事件#独立事件发生的概率$考查数据分析#数学运算的核心素养!
$解析%#!%由题易得$随机抽取一球$为黑色球或红色球的概率为.0$!’$……………………………… #分
所以D"$#($$$!’%!
数学参考答案!第!!!!’页!共"页"
{#{QQABCQqEoggAQABAABhCQQGwCgKQkBGCCIgOAAAEsAIASBFABAA=}#}所以B#D%0($=$!’0#$!………………………………………………………………………………… (分
##%甲.乙的得分情况可能为
得分情况 #$$ !($ !$$ "$ ($ ’$ $ 1!$ 1#$
! ’ !$ & !# !) " #’ !)
概率
!$$ !$$ !$$ !$$ !$$ !$$ !$$ !$$ !$$
………………………………………………………………………………………………………………… "分
! &( ’ )( !$ ’$ & !)
则甲的得分比乙的得分高$且差值大于!$$分的概率.0 = 4 = 4 = 4 = 0
!$$ !$$ !$$ !$$ !$$ !$$ !$$ !$$
&*%
0$!$&*%!…………………………………………………………………………………………… !#分
!$$$$
!"!$命题意图%本题考查数列的通项#数列求和及不等式$考查了数学运算#逻辑推理的核心素养!
$解析%#!%若选条件#-因为(
2
(
24!
0#1
2
$所以(
21!
(
2
0#1
21!
#20#%$
两式相减$得(
2
#(
24!
1(
21!
%0#(
2
#20#%!
因为( 23$$所以(
24!
1(
21!
0##20#%!
又(0!$((0#1$所以(0#$
! ! # ! #
所以数列!("的奇数项.偶数项分别是以!$#为首项$#为公差的等差数列!
2
当20#:1!$:/#4时$(
#:1!
0!4#:1!%=#0#:1!*当20#:$:/#4时$(
#:
0#4#:1!%=#0#:!
2
综上所述$(
2
02$2/#4!所以4
2
0
#2
! …………………………………………………………………… (分
若选条件$-设数列!(
2
"的公比为5$
因为!("是首项为!的等比数列$且满足($#($’( 成等差数列$
2 ! # %
! !!"21!
所以(
!
0!$且’(
#
0(
!
4’(
%
$即’50!4’5#$解得50
#
$所以(
2
0
#
!
因为数列!C"的各项均为正数$E 为其前2项和$且满足#E 0C#C4!%$
2 2 2 2 2
所以当20!时$#E 0#C0C#C4!%$则C0!$
! ! ! ! !
因为#E
2
0C
2
#C
2
4!%$所以#E
21!
0C
21!
#C
21!
4!%#20#%$
两式相减得#C
2
0C
2
#1C
2
#
1!
4C
2
1C
21!
#20#%$即#C
2
4C
21!
%#C
2
1C
21!
1!%0$#20#%!
因为C 2-$$故C
2
1C
21!
1!0$#20#%$所以C
2
1C
21!
0!#20#%!
所以数列!C"为等差数列$故C0!4#21!%=!02!
2 2
! 2
所以40 (C0 ! ……………………………………………………………………………………… (分
2 # 22 #2
若选条件%-由(
24#
4(
2
1#(
24!
0#2$得#(
24#
1(
24!
%1#(
24!
1(
2
%0#2!
令( 1(0F$则F0(1(0#$F 1F0#2!
24! 2 2 ! # ! 24! 2
当20#时$F
2
0F
!
4#F
#
1F
!
%4#F
%
1F
#
%4+4#F
2
1F
21!
%0#4#4##4+4#21!0#2$
又F0#满足上式$所以F0#2$即( 1(0#2!
! 2 24! 2
所以当20#时$(
2
0(
!
4#(
#
1(
!
%4#(
%
1(
#
%4+4#(
2
1(
21!
%0!4#4##4+4#21!0#21!!
2 2
又(0!满足上式$所以(0#21!$所以40 0 ! ……………………………………………… (分
! 2 2 (4! #2
2
2
##%证明-由#!%知40 $
2 #2
! ! ! !
则7
2
0!=
#
4#=
##
4%=
#%
4+42’
#2
#$
! ! ! ! !
所以
#
7
2
0!=
##
4#=
#%
4+4#21!%’
#2
42’
#24!
$!
数学参考答案!第!!!!(页!共"页"
{#{QQABCQqEoggAQABAABhCQQGwCgKQkBGCCIgOAAAEsAIASBFABAA=}#}#1$可得-
! !! ! ! !" ! ! 2
70 4 4 4+4 12’ 0!1 1 !
# 2 # ## #% #2 #24! #2 #24!
# 2 #42
所以70#1 1 0#1 !…………………………………………………………………………… "分
2 #2 #2 #2
#42 24#
因为
#2
-$$所以7
2
0#1
#2
##!
! 24%" ! 24#"24!
又7
24!
17
2
0 #1
#24!
1 #1
#2
0
#24!
-$$所以!7
2
"是递增数列!
!4# ! !
所以7 207
!
0#1
#!
0
#
$故
#
17 2##!……………………………………………………………… !#分
#$!$命题意图%本题考查空间几何体的线面位置关系#二面角$考查了直观想象#逻辑推理#数学运算的核心素养!
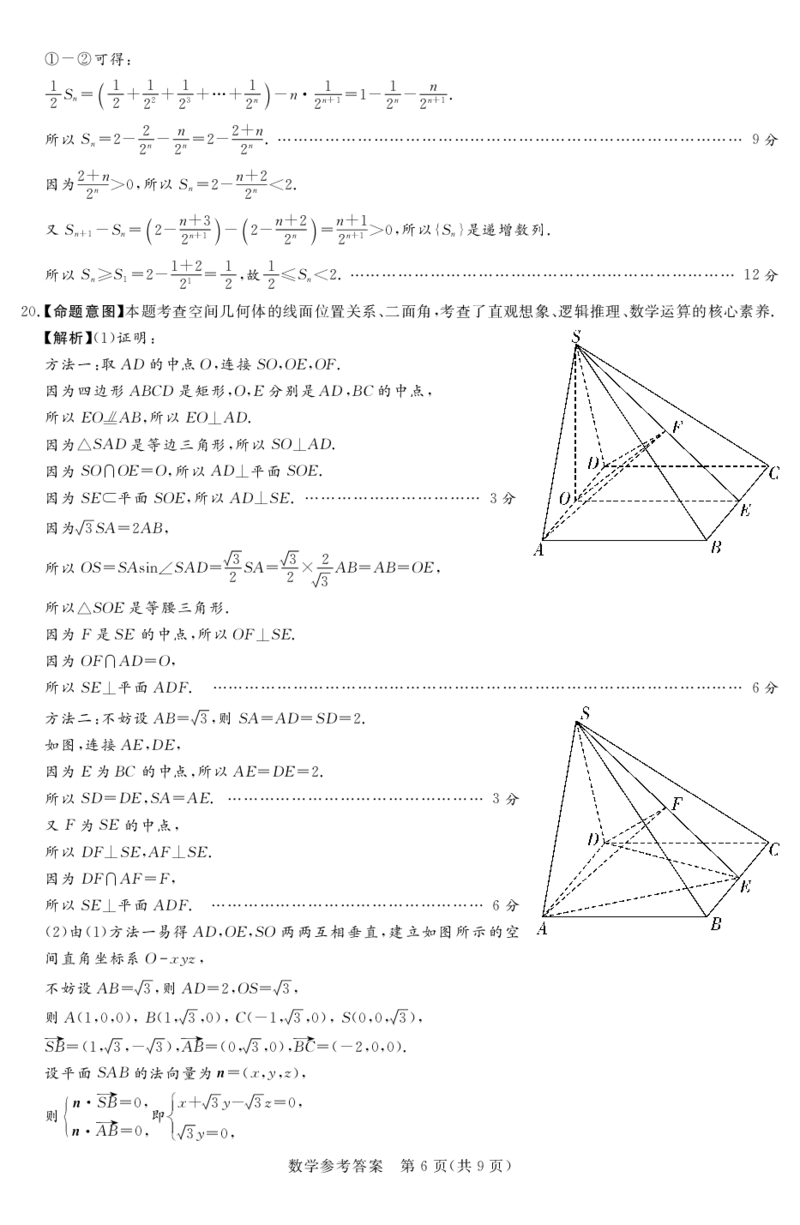
$解析%#!%证明-
方法一-取"*的中点=$连接7=$=B$=,!
因为四边形"$’*是矩形$=$B分别是"*$$’的中点$
所以B=5"$$所以B=)"*!
因为*7"*是等边三角形$所以7=)"*!
因为7=%=B0=$所以"*)平面7=B!
因为7B2平面7=B$所以"*)7B!…………………………… %分
因为槡%7"0#"$$
槡% 槡% #
所以=707";63,7"*0 7"0 = "$0"$0=B$
# # 槡%
所以*7=B是等腰三角形!
因为,是7B的中点$所以=,)7B!
因为=,%"*0=$
所以7B)平面"*,! ……………………………………………………………………………………… )分
方法二-不妨设"$0槡%$则7"0"*07*0#!
如图$连接"B$*B$
因为B为$’的中点$所以"B0*B0#!
所以7*0*B$7"0"B!………………………………………… %分
又,为7B的中点$
所以*,)7B$",)7B!
因为*,%",0,$
所以7B)平面"*,! …………………………………………… )分
##%由#!%方法一易得"*$=B$7=两两互相垂直$建立如图所示的空
间直角坐标系= #%&$
不妨设"$0槡%$则"*0#$=70槡%$
则"#!$$$$%$$#!$槡%$$%$’#1!$槡%$$%$7#$$$$槡%%$
776 776 776
7$0#!$槡%$1槡%%$"$0#$$槡%$$%$$’0#1#$$$$%!
设平面7"$的法向量为$0##$%$&%$
776
%$’7$0$$ ’#4槡%%1槡%&0$$
则 即&
776
$’"$0$$ (槡%%0$$
数学参考答案!第!!!!)页!共"页"
{#{QQABCQqEoggAQABAABhCQQGwCgKQkBGCCIgOAAAEsAIASBFABAA=}#}令#0槡%$则&0!$%0$$
所以平面7"$的一个法向量为$0#槡%$$$!%!…………… &分
设平面7$’的法向量为%0##<$%<$&<%$
776
%%’7$0$$ %#<4槡%%<1槡%&<0$$
则 即
776
%’$’0$$ 1##<0$$
令%<0!$则#<0$$&<0!$
所以平面7$’的一个法向量为%0#$$!$!%!…………… !$分
设二面角" 7$ ’的平面角为$$则
"$’%" "槡%=$4$=!4!=!" 槡#
"9:;$"0 0 0 $
"$""%" #=槡# ’
所以;63$0槡!1
!槡#"#
0
槡!’
!
’ ’
槡!’
所以二面角" 7$ ’的正弦值为 !………………………………………………………………… !#分
’
#!!$命题意图%本题考查椭圆的方程#直线与椭圆的位置关系及定点问题$考查了直观想象#数学运算#逻辑推
理等核心素养!
$解析%#!%因为,,
!
G,
#
的最大值为!#$<$
C 槡%
所以G为短轴的顶点时$,,
!
G,
#
0!#$<$此时易得
4
0
#
!
又点G到右焦点, 距离的最小值为#1槡%$即41C0#1槡%$解得40#$C0槡%!
#
又由4#0(#4C#$可得(0!!
##
所以椭圆’的标准方程为 4%#0!!……………………………………………………………………… ’分
’
##%证明-
%#03$
方法一-当直线+的斜率不存在时$设+-#03$联立
##4’%#0’$
解得%0@槡!1
3#
$所以.
!
3$槡!1
3#"
$H
!
3$1槡!1
3#"
或.
!
3$1槡!1
3#"
$H
!
3$槡!1
3#"
!
’ ’ ’ ’ ’
又"##$$%$所以" 776 .0 ! 31#$槡!1 3#" $" 776 H0 ! 31#$1槡!1 3#" 或" 776 .0 ! 31#$1槡!1 3#" $" 776 H0
’ ’ ’
!
31#$槡!1
3#"
$
’
因为以.H为直径的圆恒过点"$所以".)"H!
776 776 ! 3#" )
所以".’"H0#31#%#1 !1 0$$解得30 或30##舍去%$
’ (
)
此时直线+的方程为#0 !………………………………………………………………………………… )分
(
当直线+的斜率存在时$易知直线+的斜率不为$$设+-%0:#42$
%%0:#42$
联立 消去%得#’:#4!%##4&:2#4’#2#1!%0$!
##4’%#0’$
由#-$$得’:#12#4!-$$
&:2 ’#2#1!%
由根与系数的关系$知#4#01 $##0 !…………………………………………… &分
! # ’:#4! ! # ’:#4!
数学参考答案!第!!!!*页!共"页"
{#{QQABCQqEoggAQABAABhCQQGwCgKQkBGCCIgOAAAEsAIASBFABAA=}#}776 776
因为".0##
!
1#$%! %$"H0##
#
1#$%# %$
776 776
所以".’"H0##
!
1#%##
#
1#%4%!%# 0#:#4!%#
!
#
#
4#:21#%##
!
4#
#
%4#2#4’%0$$
&:2 ’#2#1!%
将#4#01 $##0 代入上式整理得!#:#4(2#4!):20$$
! # ’:#4! ! # ’:#4!
)
即#):4(2%##:42%0$$所以201 :或201#:!
(
当201#:时$直线+为%0:#1#:0:##1#%$此时直线+过点"$不符合题意$舍去*
) ! )" !) "
当201 :时$直线+为%0:#1 $此时直线+过定点 $$ !………………………………… !!分
( ( (
!) "
综上所述$直线+恒过定点 $$ !……………………………………………………………………… !#分
(
方法二-
由题意知$直线+的斜率不为零$设直线+的方程为#03%42!
%#03%42$
联立 得#’43#%%#4#32%42#1’0$!
##4’%#0’$
由#-$$得3#12#4’-$!
#32 2#1’
所以%! 4%# 01
3#4’
$%!%# 0
3#4’
! …………………………………………………………………… )分
776 776
因为"##$$%$所以".0##
!
1#$%! %$"H0##
#
1#$%# %!
776 776 776 776
由题易知".)"H$所以".’"H0##
!
1#%##
#
1#%4%!%# 0$!
即#
!
#
#
1###
!
4#
#
%4%!%# 4’0$$
即#3#4!%%!%# 4#321#3%#%! 4%# %42#1’24’0$! ………………………………………………… &分
#32 2#1’
将%! 4%# 01
3#4’
$%!%# 0
3#4’
代入上式整理得(2#1!)24!#0$$
)
解得20#或20 ! ……………………………………………………………………………………… !$分
(
)
由题知直线+不过点"$所以20 !
(
)
所以直线+的方程为#03%4 !
(
!) "
所以直线+恒过定点 $$ !……………………………………………………………………………… !#分
(
方法三#平移齐次化%-
##4#%#
将椭圆向左平移两个单位长度得曲线’<- 4%#0!$
’
##
即 4#4%#0$#$则平移后右顶点"<#$$$%$记平移后.$H的对应点分别为.<$H