石室阳安中学高三上(开学考)-文数试题+答案(1)_2023年9月_029月合集_2024届四川省成都市石室阳安中学高三上学期开学考

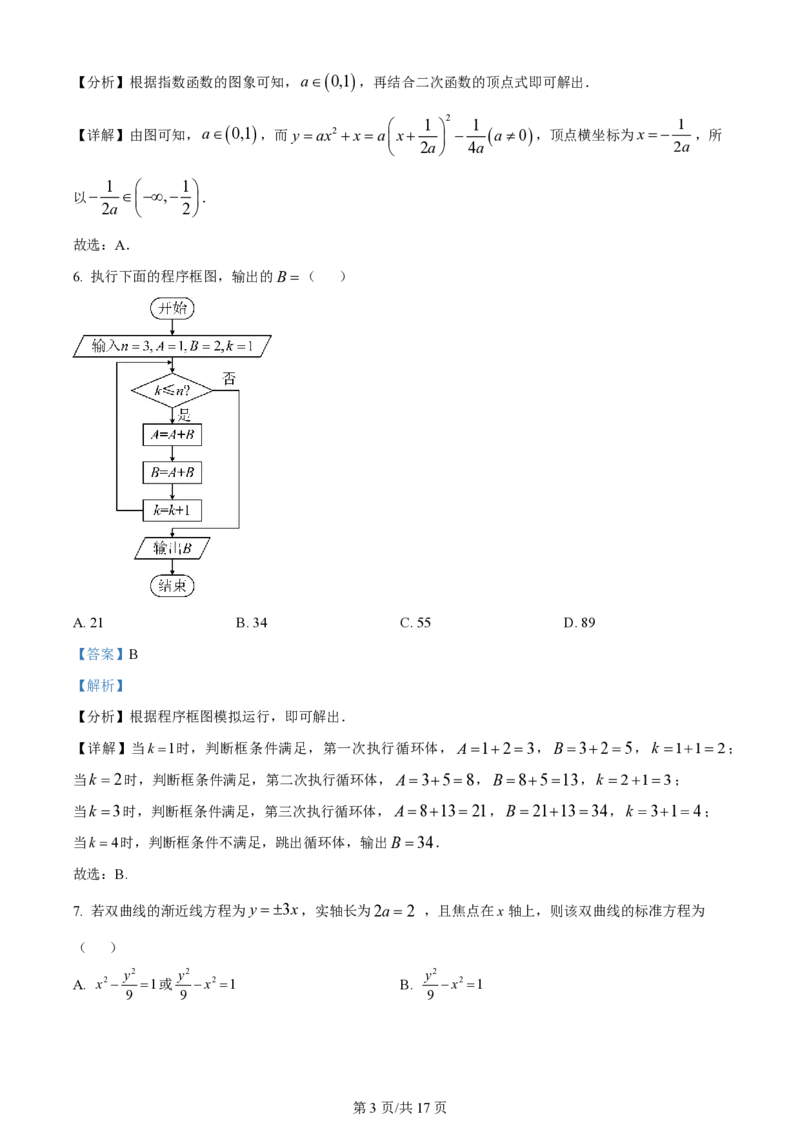
成都石室阳安高三数学（文科）入学考试 一、选择题：本题共 12小题，每小题 5分，共 60分.在每小题给出的四个选项中，只有一项 是符合题目 Ax|1 x1 Bx|0 x2 1. 已知集合 ， ，则AB（ ） A. x|1x2 B. x|1 x2 C. x|0 x1 D. x|0 x2 2 2. 已知i为虚数单位，则 （ ） 1i A. 1i B. 1i C. 12i D. 12i x3,x0 3. 已知函数 f x ,若 f x8，则x＝（ ） 2x,x0 A. －3 B. －2 C. 3 D. 3或－2 x2y40  4. 已知实数x，y满足不等式组2x y40，则目标函数z 3x y的最大值为（ ）  x y0  8 A 0 B. C. 4 D. 8 . 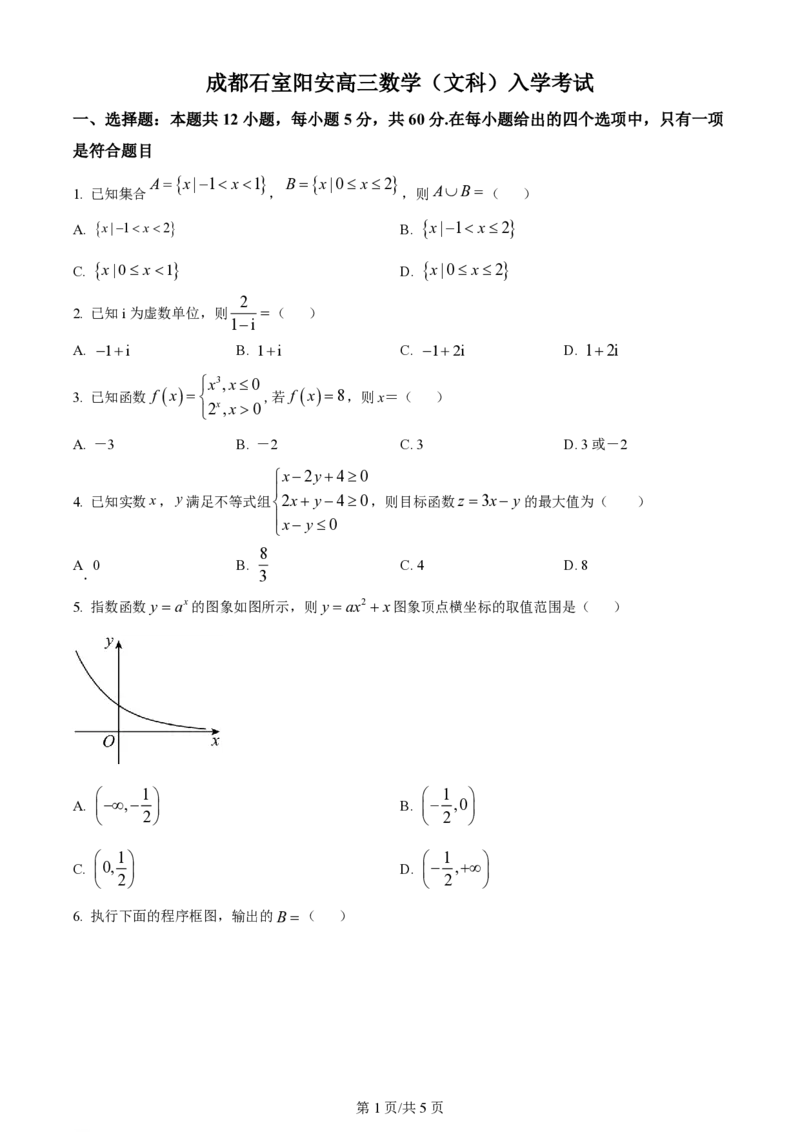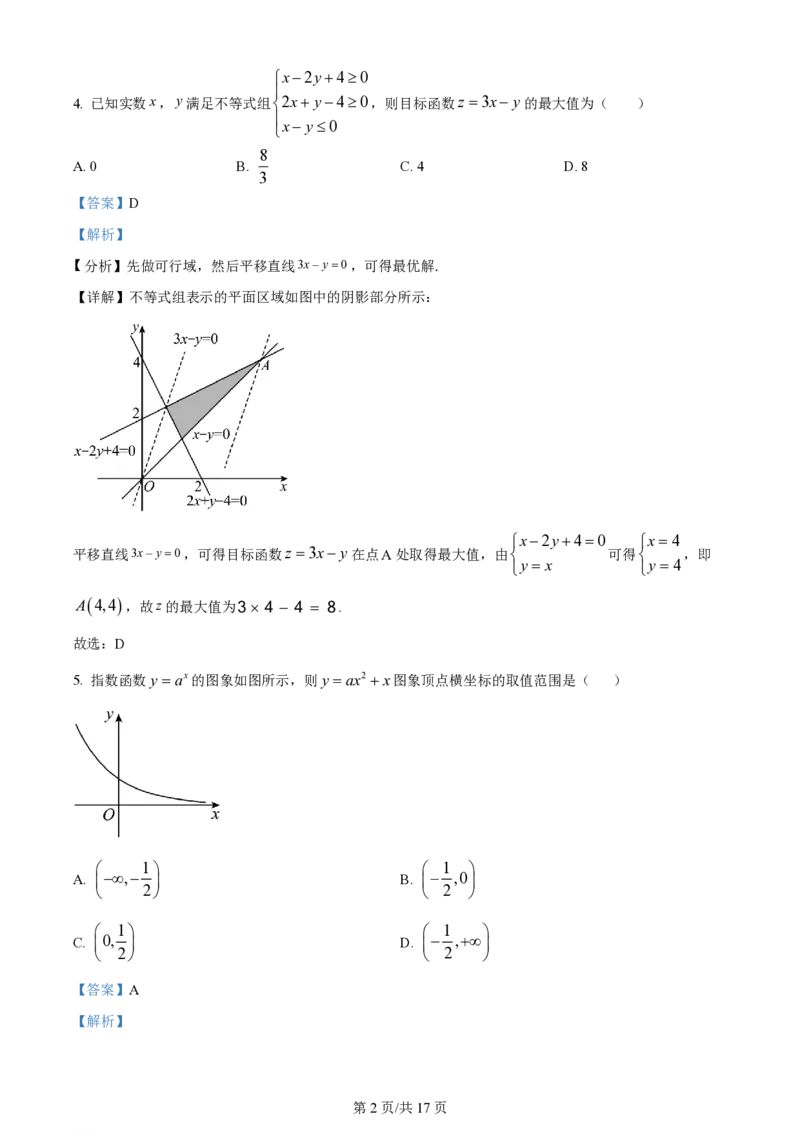3 5. 指数函数y ax的图象如图所示，则y ax2 x图象顶点横坐标的取值范围是（ ）  1  1  A.  ,  B.   ,0   2  2   1  1  C.  0,  D.   ,   2  2  6. 执行下面的程序框图，输出的B（ ） 第1页/共5页 学科网（北京）股份有限公司A. 21 B. 34 C. 55 D. 89 7. 若双曲线的渐近线方程为y 3x，实轴长为2a2 ，且焦点在x轴上，则该双曲线的标准方程为 （ ） y2 y2 y2 A. x2 1或 x2 1 B. x2 1 9 9 9 y2 x2 C. x2 1 D. y2 1 9 9 8. 设，为不同的平面，m，n为不同的直线，n ，n，则“m”是“m”的（ ） A. 充要条件 B. 必要不充分条件 C. 充分不必要条件 D. 既不充分也不必要条件 a log 3 9. 已知 1 ，be0.5，cln2，则（ ） 2 A. a＞b＞c B. b＞a＞c C. b＞c＞a D. 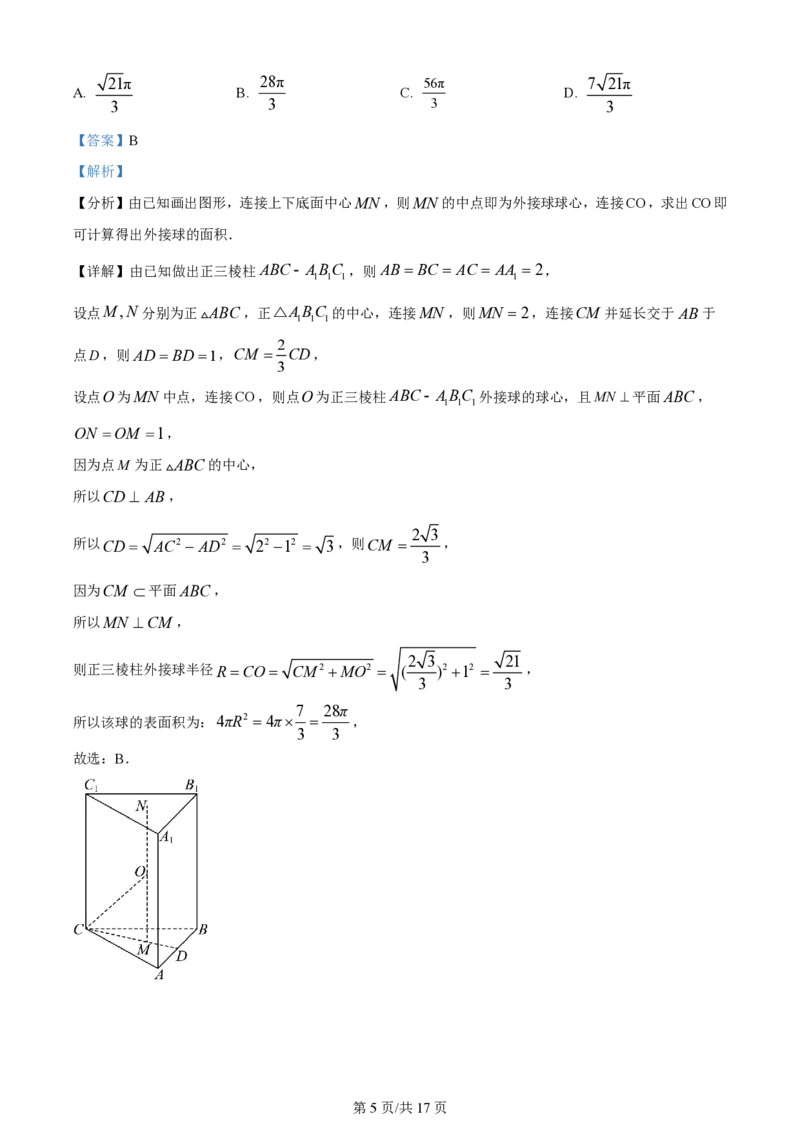c＞b＞a 10. 在一个正三棱柱中，所有棱长都为2，各顶点都在同一个球面上，则该球的表面积为（ ） 21π 28π 56π 7 21π A B. C. D. . 3 3 3 3 2 11. 若函数 f x x2 alnx 在 1, 上为单调递增函数，则a的取值范围为（ ） x A. ,0 B. ,4 C. 4, D. 0, 12. 已知可导函数 f(x)的导函数为 f(x)，若对任意的xR，都有 f(x) f(x)1，且 f(0)2021， 则不等式 f(x)2020ex 1的解集为（ ） A. (,e) 第2页/共5页 学科网（北京）股份有限公司B. (,2021) C. (0,) D. (2020,) 二、填空题：本题共 4小题，每小题 5分，共 20分. 13. 在区间 1,1 内随机取一个数k，使直线y kx与圆x22  y2 1相交的概率为______. 5  1 14 计算lg 2lg23log 3 2 0.25 2 ______. . 2 1 3 15. 已知x0,y 0， 且x y 2，则  的最小值为________． x y 1  16. 若x  ,2  ，使2x2 x10成立是假命题，则实数的取值范围是___________. 2  三、解答题：本题共 6小题，共 70分.解答应写出文字说明、证明过程或演算步骤 1 17. 已知函数 f(x) x3 ax2 3x． 3 （1）若 f x 在点  1, f 1 处的切线与直线y 4x1平行，求实数a的值； （2）当a 1时，求函数 f x 的单调区间． 18. 现在的高一年级学生将会是四川省首届参加新高考的学生，高考招生计划按历史科目组合与物理科目 组合分别编制．为了了解某校高一学生的物理学习情况，在一次全年级物理测试后随机抽取了100名学生 的物理成绩，将成绩分为 40,50 ， 50,60 ， 60,70 ， 70,80 ， 80,90 ， 90,100 共6组，得到如 图所示的频率分布直方图，记分数低于60分为不及格． （1）求直方图中a的值，并估计本次物理测试的及格率； （2）在样本中，采取分层抽样的方法从成绩不及格的学生中抽取6名作试卷分析，再从这6名学生中随 机抽取2名做面对面交流，求2名面对面交流学生的成绩均来自 50,60 的概率． 第3页/共5页 学科网（北京）股份有限公司19. 如图，在多面体ABCDEF 中，四边形ABCD为正方形，DE平面ABCD，DE∥BF ， AD DE 2，BF 1． （1）证明：AC  EF； （2）求三棱锥F AEC 的体积． x2 y2 20. 已知椭圆C：  1a b0的离心率为 1 ，过椭圆右焦点F的直线l与椭圆交于A，B两 a2 b2 2 点，当直线l与x轴垂直时， AB 3． （1）求椭圆C的标准方程； （2）当直线l的斜率为k k 0 时，在x轴上是否存在一点P（异于点F），使x轴上任意一点到直线PA 与到直线PB的距离相等？若存在，求P点坐标；若不存在，请说明理由． 21. 函数 f(x)(x2)ex ax2 2ax，aR． （1）当a0时，证明： f xe0； （2）若x1是 f x 的一个极大值点，求实数a的取值范围． （二）选考题：共 10分.请考生在第 22、23题中任选一题作答.如果多做，则按所做的第一 题计分. [坐标系与参数方程] x2cos, 22. 在平面直角坐标系xoy中，曲线C的参数方程为 （为参数）．以坐标原点为极点，x y 2sin π 轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为 (R)． 3 （1）求曲线C的极坐标方程； 1 1 （2）若直线l与曲线C交于M,N 两点，求  ． OM ON [不等式选讲] 第4页/共5页 学科网（北京）股份有限公司23. 已知 f x x3,gx6 x1 ． （1）若 f xgx ，求x的取值范围； （2）若不等式 f xgx2a2 5a的解集为R ，求实数a的取值范围． 第5页/共5页 学科网（北京）股份有限公司成都石室阳安高三数学（文科）入学考试 一、选择题：本题共 12小题，每小题 5分，共 60分.在每小题给出的四个选项中，只有一项 是符合题目 Ax|1 x1 Bx|0 x2 1. 已知集合 ， ，则AB（ ） A. x|1x2 B. x|1 x2 C. x|0 x1 D. x|0 x2 【答案】B 【解析】 【分析】结合题意利用并集的定义计算即可. 【详解】由题意可得：A  Bx|1 x2 . 故选：B . 2 2. 已知i为虚数单位，则 （ ） 1i A. 1i B. 1i C. 12i D. 12i 【答案】B 【解析】 【分析】利用复数计算公式直接化简得到答案. 2 21i 【详解】  1i 1i 1i1i 故选：B x3,x0 3. 已知函数 f x ,若 f x8，则x＝（ ） 2x,x0 A. －3 B. －2 C. 3 D. 3或－2 【答案】C 【解析】 【分析】分x0与x0两种情况，求出答案. 【详解】当x0时，x3 8，解得x2，不满足要求，舍去； 当x0时，2x 8，解得x3，满足要求. 故选：C 第1页/共17页 学科网（北京）股份有限公司x2y40  4. 已知实数x，y满足不等式组2x y40，则目标函数z 3x y的最大值为（ ）  x y0  8 A. 0 B. C. 4 D. 8 3 【答案】D 【解析】 【分析】先做可行域，然后平移直线3xy0，可得最优解. 【详解】不等式组表示的平面区域如图中的阴影部分所示： x2y40 x4 平移直线3xy0，可得目标函数z 3x y在点A处取得最大值，由 可得 ，即 y  x y 4 A4,4 ，故z的最大值为3 4  4  8. 故选：D 5. 指数函数y ax的图象如图所示，则y ax2 x图象顶点横坐标的取值范围是（ ）  1  1  A.  ,  B.   ,0   2  2   1  1  C.  0,  D.   ,   2  2  【答案】A 【解析】 第2页/共17页 学科网（北京）股份有限公司【分析】根据指数函数的图象可知，a0,1 ，再结合二次函数的顶点式即可解出． 【详解】由图可知，a0,1 ，而y ax2 xa  x 1  2  1 a0，顶点横坐标为x 1 ，所    2a 4a 2a 1  1 以   , ． 2a  2 故选：A． 6. 执行下面的程序框图，输出的B（ ） A. 21 B. 34 C. 55 D. 89 【答案】B 【解析】 【分析】根据程序框图模拟运行，即可解出． 【详解】当k1时，判断框条件满足，第一次执行循环体， A123，B325，k 112； 当k 2时，判断框条件满足，第二次执行循环体，A358，B8513，k 213； 当k 3时，判断框条件满足，第三次执行循环体，A81321，B211334，k 314； 当k 4时，判断框条件不满足，跳出循环体，输出B34． 故选：B. 7. 若双曲线的渐近线方程为y 3x，实轴长为2a2 ，且焦点在x轴上，则该双曲线的标准方程为 （ ） y2 y2 y2 A. x2 1或 x2 1 B. x2 1 9 9 9 第3页/共17页 学科网（北京）股份有限公司y2 x2 C. x2 1 D. y2 1 9 9 【答案】C 【解析】 【分析】根据双曲线的性质求解. b  3 a 1 【详解】由题可得a ，解得 ，  2a 2 b3 y2 因为焦点在x轴上，所以双曲线的标准方程为x2 1. 9 故选:C. 8. 设，为不同的平面，m，n为不同的直线，n ，n，则“m”是“m”的（ ） A. 充要条件 B. 必要不充分条件 C. 充分不必要条件 D. 既不充分也不必要条件 【答案】A 【解析】 【分析】利用线面垂直和面面平行的知识即可判断. 【详解】因为n ，n，所以∥， 若m，则m； 若m，则m. 故选：A a log 3 9. 已知 1 ，be0.5，cln2，则（ ） 2 A. a＞b＞c B. b＞a＞c C. b＞c＞a D. c＞b＞a 【答案】C 【解析】 【分析】根据指数函数、对数函数的性质判断即可. a log 3log 30 【详解】因为 1 2 ，0cln2lne1，be0.5 e0 1， 2 e0.5 ln2log 2 所以 1 ，即bca. 2 故选：C 10. 在一个正三棱柱中，所有棱长都为2，各顶点都在同一个球面上，则该球的表面积为（ ） 第4页/共17页 学科网（北京）股份有限公司21π 28π 56π 7 21π A. B. C. D. 3 3 3 3 【答案】B 【解析】 【分析】由已知画出图形，连接上下底面中心MN ，则MN 的中点即为外接球球心，连接CO，求出CO即 可计算得出外接球的面积． 【详解】由已知做出正三棱柱ABC- ABC ，则AB BC  AC  AA 2， 1 1 1 1 设点M,N 分别为正 ABC，正△ABC 的中心，连接MN ，则MN 2，连接CM 并延长交于AB于  1 1 1 2 点D，则AD BD1，CM  CD， 3 设点O为MN 中点，连接CO，则点O为正三棱柱ABC- ABC 外接球的球心，且MN 平面ABC， 1 1 1 ON OM 1， 因为点M 为正 ABC的中心，  所以CD AB， 2 3 所以CD  AC2  AD2  22 12  3，则CM  ， 3 因为CM 平面ABC， 所以MN CM ， 2 3 21 则正三棱柱外接球半径RCO CM2 MO2  ( )2 12  ， 3 3 7 28π 所以该球的表面积为：4πR2 4π  ， 3 3 故选：B． 第5页/共17页 学科网（北京）股份有限公司2 11. 若函数 f x x2 alnx 在 1, 上为单调递增函数，则a的取值范围为（ ） x A. ,0 B. ,4 C. 4, D. 0, 【答案】D 【解析】 2 【分析】转化为 f(x)0，即a 2x2在 1, 上恒成立，再根据右边构造函数，利用导数求出最大 x 值可得结果. a 2 2x3ax2 【详解】 f(x)2x   ， x x2 x2 因为 f(x)在 1, 上为单调递增函数， 所以 f(x)0在 1, 上恒成立， 2 则2x3 ax20，即a 2x2在 1, 上恒成立， x 2 2 设g(x) 2x2(x1)，则g(x) 4x0，g(x)在 1, 上为减函数， x x2 g(x) g(1)0，所以a0. 故选：D 12. 已知可导函数 f(x)的导函数为 f(x)，若对任意的xR，都有 f(x) f(x)1，且 f(0)2021， 则不等式 f(x)2020ex 1的解集为（ ） A. (,e) B. (,2021) C. (0,) D. (2020,) 【答案】C 【解析】 f(x)1 【分析】构函数g(x) ，由题设条件可得其单调性，从而可求函数不等式的解. ex f(x)1 f(x) f(x)1 【详解】构造函数g(x) ，则g(x) 0， ex ex 第6页/共17页 学科网（北京）股份有限公司f(0)1 ∴函数g(x)在R上单调递减，∵ f(0)2021，∴g(0) 2020， e0 f(x)1 由 f(x)2020ex 1得 2020，∴g(x) g(0)， ex ∵函数g(x)在R上单调递减，∴x0， 故选：C. 二、填空题：本题共 4小题，每小题 5分，共 20分. 13. 在区间 1,1 内随机取一个数k，使直线y kx与圆x22  y2 1相交的概率为______. 3 【答案】 3 【解析】 【分析】根据题意，由直线与圆相交列出不等式即可得到k的范围，再结合几何概型的概率计算公式即可 得到结果． 【详解】因为圆心(2,0)，半径r 1，直线与圆相交， |2k| 3 3 所以圆心到直线y kx的距离d  1，解得 k  ， 1k2 3 3 2 3 所以所求的概率为 3 3 ．  2 3 3 故答案为： 3 5  1 14. 计算lg 2lg23log 3 2 0.25 2 ______. 2 【答案】5 【解析】 【分析】 运用对数，指数的运算性质求解运算. 1  【详解】lg 5 2lg23log 3 2 0.25  1 2 lg 5 lg22 2     1  2  2 2 2  2  1 5 1 lg 42 lg104145   2 2 第7页/共17页 学科网（北京）股份有限公司故答案为：5 1 3 15. 已知x0,y 0， 且x y 2，则  的最小值为________． x y 【答案】2 3 【解析】 1 3 【分析】根据基本不等式，结合“1”的代换，可求得  的最小值． x y x y 【详解】因为x y 2，即  1 2 2 1 3 所以   1  x y 1 3  x y          x y 2 2 1 3 y 3x     2 2 2x 2y y 3x 22  2x 2y y 3x  2 3，当且仅当  时取得等号 2x 2y 1 3 所以  的最小值为2 3 x y 【点睛】本题考查了基本不等式的简单应用，属于基础题． 1  16. 若x  ,2  ，使2x2 x10成立是假命题，则实数的取值范围是___________. 2  【答案】2 2 【解析】 1  【分析】转化为“x  ,2  ，使得2x2 x10成立”是真命题，利用不等式的基本性质分离参数， 2  利用函数的单调性求相应最值即可得到结论. 1  【详解】若x  ,2  ，使2x2 x10成立是假命题， 2  第8页/共17页 学科网（北京）股份有限公司1  则“x  ,2  ，使得2x2 x10成立”是真命题， 2  1  2x2 1 1 即x ,2 ， 2x 恒成立，   2  x x 1 1 2 因为2x 2 2x =2 2，x 时等号成立， x x 2  1 所以 2x  2 2，  x min 所以2 2， 故答案为：2 2. 三、解答题：本题共 6小题，共 70分.解答应写出文字说明、证明过程或演算步骤 1 17. 已知函数 f(x) x3 ax2 3x． 3 （1）若 f x 在点  1, f 1 处的切线与直线y 4x1平行，求实数a的值； （2）当a 1时，求函数 f x 的单调区间． 【答案】（1）1 （2）单调递增区间为 ,1 ， 3, ，单调递减区间为 1,3 . 【解析】 【分析】（1）求出函数的导函数，依题意可得 f14，代入计算可得； （2）求出函数的导函数，再解关于导函数的不等式，即可求出函数的单调区间. 【小问1详解】 1 因为 f(x) x3 ax2 3x，所以 f(x) x2 2ax3， 3 因为 f x 在点  1, f 1 处的切线与直线y 4x1平行，所以 f14， 即12a34，解得a 1. 【小问2详解】 1 当a 1时 f(x) x3 x2 3x，则 f(x)x2 2x3x1x3， 3 令 f(x)0，解得x1或x3，所以 f x 的单调递增区间为 ,1 ， 3, ， 令 f(x)0，解得1 x3，所以 f x 的单调递减区间为 1,3 . 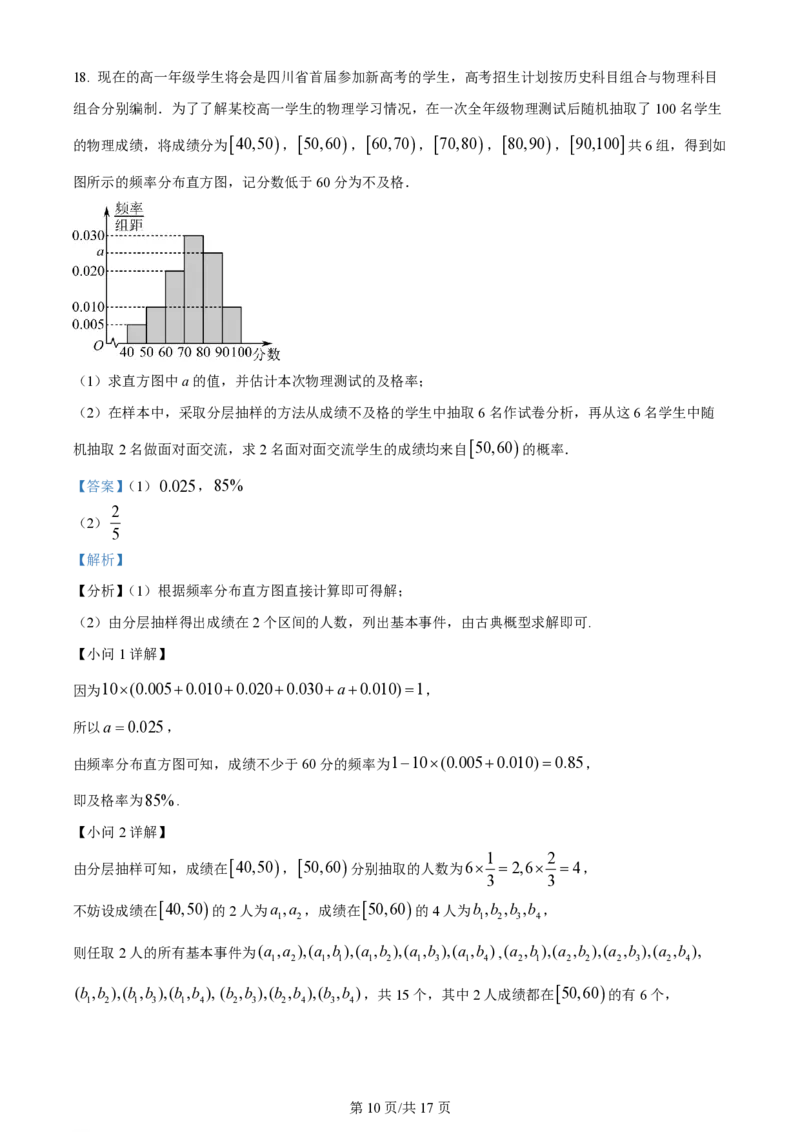第9页/共17页 学科网（北京）股份有限公司18. 现在的高一年级学生将会是四川省首届参加新高考的学生，高考招生计划按历史科目组合与物理科目 组合分别编制．为了了解某校高一学生的物理学习情况，在一次全年级物理测试后随机抽取了100名学生 的物理成绩，将成绩分为 40,50 ， 50,60 ， 60,70 ， 70,80 ， 80,90 ， 90,100 共6组，得到如 图所示的频率分布直方图，记分数低于60分为不及格． （1）求直方图中a的值，并估计本次物理测试的及格率； （2）在样本中，采取分层抽样的方法从成绩不及格的学生中抽取6名作试卷分析，再从这6名学生中随 机抽取2名做面对面交流，求2名面对面交流学生的成绩均来自 50,60 的概率． 【答案】（1）0.025，85% 2 （2） 5 【解析】 【分析】（1）根据频率分布直方图直接计算即可得解； （2）由分层抽样得出成绩在2个区间的人数，列出基本事件，由古典概型求解即可. 【小问1详解】 因为10(0.0050.0100.0200.030a0.010)1， 所以a0.025， 由频率分布直方图可知，成绩不少于60分的频率为110(0.0050.010)0.85， 即及格率为85%. 【小问2详解】 1 2 由分层抽样可知，成绩在 40,50 ， 50,60 分别抽取的人数为6 2,6 4， 3 3 不妨设成绩在 40,50 的2人为a ,a ，成绩在 50,60 的4人为b,b ,b ,b ， 1 2 1 2 3 4 则任取2人的所有基本事件为(a ,a ),(a ,b),(a ,b ),(a ,b ),(a ,b ),(a ,b),(a ,b ),(a ,b ),(a ,b ), 1 2 1 1 1 2 1 3 1 4 2 1 2 2 2 3 2 4 (b,b ),(b,b ),(b,b ), (b ,b ),(b ,b ),(b ,b )，共15个，其中2人成绩都在 50,60 的有6个， 1 2 1 3 1 4 2 3 2 4 3 4 第10页/共17页 学科网（北京）股份有限公司6 2 所以由古典概型知P  . 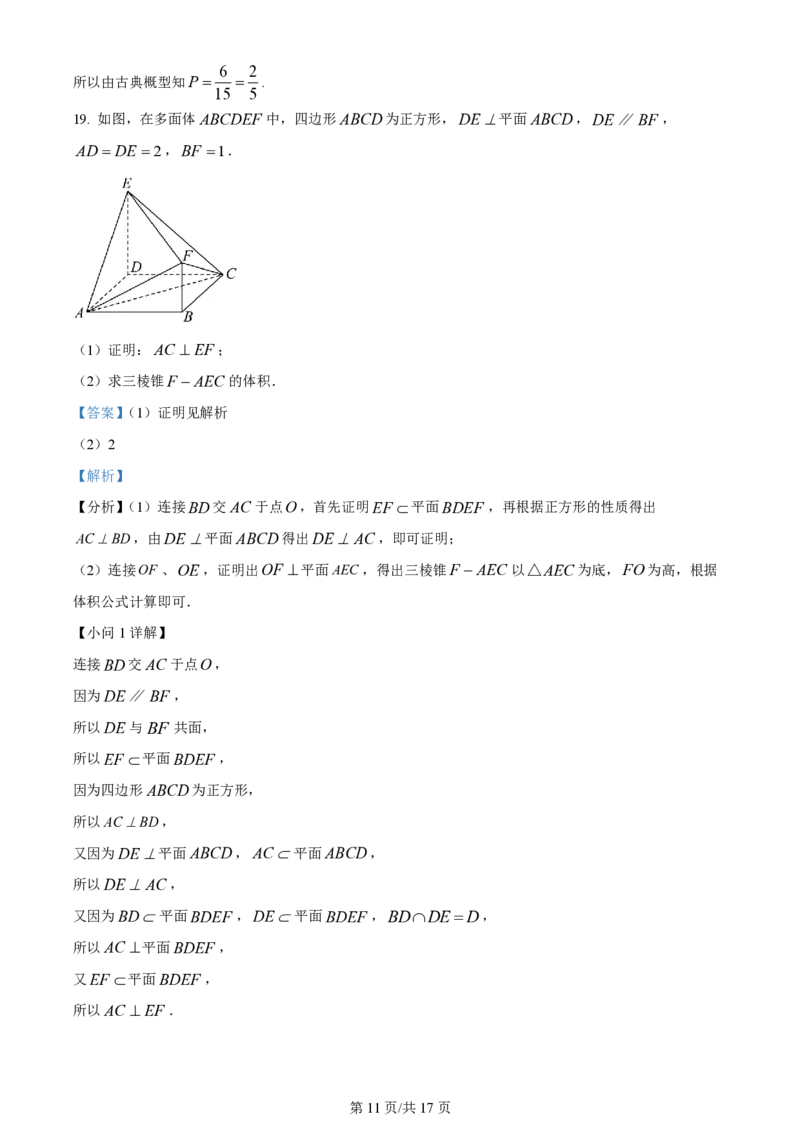15 5 19. 如图，在多面体ABCDEF 中，四边形ABCD为正方形，DE平面ABCD，DE∥BF ， AD DE 2，BF 1． （1）证明：AC  EF； （2）求三棱锥F AEC 的体积． 【答案】（1）证明见解析 （2）2 【解析】 【分析】（1）连接BD交AC于点O，首先证明EF 平面BDEF ，再根据正方形的性质得出 ACBD，由DE平面ABCD得出DEAC，即可证明； （2）连接OF 、OE，证明出OF 平面AEC，得出三棱锥F AEC 以△AEC为底，FO为高，根据 体积公式计算即可． 【小问1详解】 连接BD交AC于点O， 因为DE∥BF ， 所以DE与BF 共面， 所以EF 平面BDEF ， 因为四边形ABCD为正方形， 所以ACBD， 又因为DE平面ABCD，AC平面ABCD， 所以DEAC， 又因为BD平面BDEF ，DE平面BDEF ，BDDED， 所以AC 平面BDEF ， 又EF 平面BDEF ， 所以AC  EF． 第11页/共17页 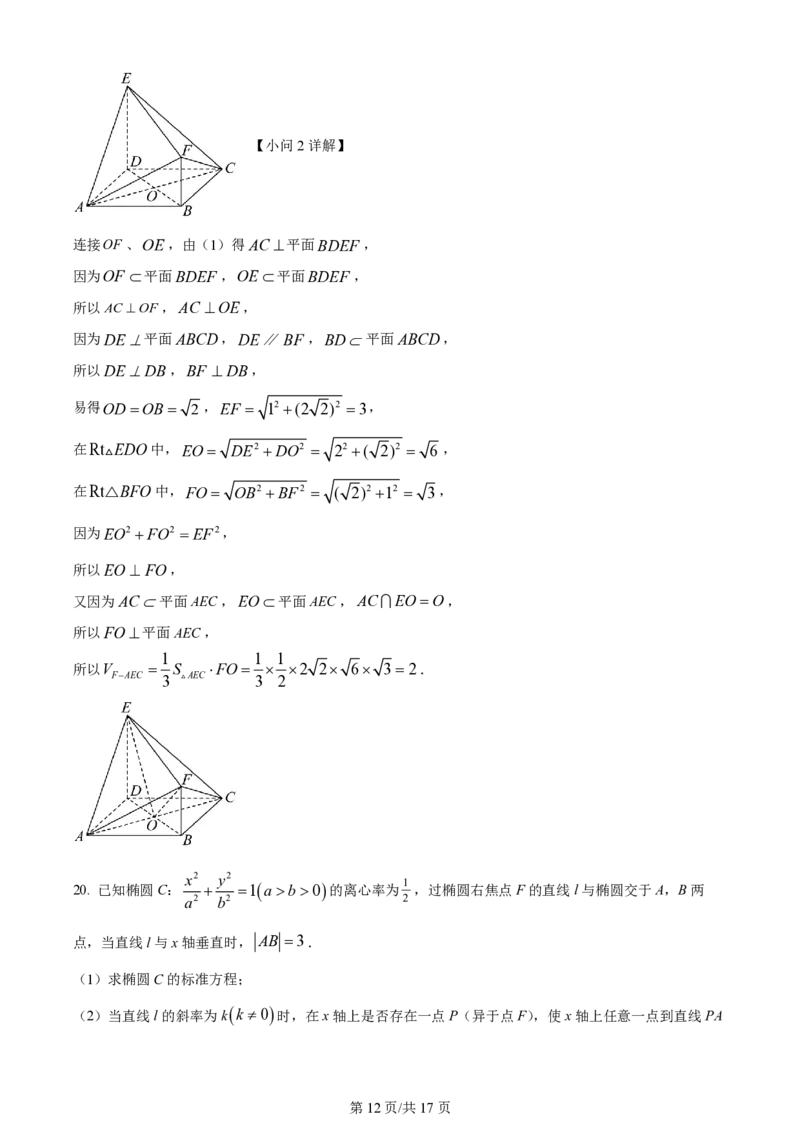学科网（北京）股份有限公司【小问2详解】 连接OF 、OE，由（1）得AC 平面BDEF ， 因为OF 平面BDEF ，OE 平面BDEF ， 所以AC OF，AC OE， 因为DE平面ABCD，DE∥BF ，BD平面ABCD， 所以DEDB，BF  DB， 易得ODOB 2，EF  12 (2 2)2 3， 在Rt  EDO中，EO DE2 DO2  22 ( 2)2  6 ， 在Rt△BFO中，FO OB2 BF2  ( 2)2 12  3， 因为EO2 FO2  EF2， 所以EO  FO， 又因为AC平面AEC，EO平面AEC，AC  EOO， 所以FO平面AEC， 1 1 1 所以V  S FO  2 2 6 3 2． FAEC 3 AEC 3 2 x2 y2 20. 已知椭圆C：  1a b0的离心率为 1 ，过椭圆右焦点F的直线l与椭圆交于A，B两 a2 b2 2 点，当直线l与x轴垂直时， AB 3． （1）求椭圆C的标准方程； （2）当直线l的斜率为k k 0 时，在x轴上是否存在一点P（异于点F），使x轴上任意一点到直线PA 第12页/共17页 学科网（北京）股份有限公司与到直线PB的距离相等？若存在，求P点坐标；若不存在，请说明理由． x2 y2 【答案】（1）  1 4 3 （2）存在，P4,0 【解析】 【分析】（1）根据题意列式求解a,b,c，即可得结果； （2）根据题意分析可得x轴为直线PA与直线PB的对称轴，根据斜率关系结合韦达定理运算求解. 【小问1详解】 设椭圆C的半焦距为c0，  a2 b2 c2 a 2  2b2  由题意可得 3 ，解得b 3， a   c1  c 1  e    a 2 x2 y2 所以椭圆C的标准方程为  1. 4 3 【小问2详解】 由（1）可得：F1,0 ， 根据题意可设直线l: y kx1,Ax ,y ,Bx ,y ,Pm,0m1 ， 1 1 2 2 y kx1  联立方程x2 y2 ，消去y得  4k2 3  x2 8k2x4k2 120，   1  4 3 则64k2 4  4k2 3  4k2 12  144  k2 1  0， 8k2 4k2 12 可得x x  ,x x  ，① 1 2 4k2 3 1 2 4k2 3 y y 由题意可知x轴为直线PA与直线PB的对称轴，则k k  1  2 0， PA PB x m x m 1 2 kx 1 kx 1 可得 1  2 0， x m x m 1 2 第13页/共17页 学科网（北京）股份有限公司因为k 0，可得 x 1x mx mx 10， 1 2 1 2 整理得2x x m1x x 2m0，② 1 2 1 2 2  4k2 12  8k2m1 将①代入②得：  2m0，解得m4， 4k2 3 4k2 3 所以存在点P，使x轴上任意一点到直线PA与到直线PB的距离相等，此时P4,0 . 【点睛】方法点睛：存在性问题求解的思路及策略 （1）思路：先假设存在，推证满足条件的结论，若结论正确则存在；若结论不正确则不存在． （2）策略：①当条件和结论不唯一时要分类讨论； ②当给出结论而要推导出存在的条件时，先假设成立，再推出条件； ③当条件和结论都不知，按常规法解题很难时，可先由特殊情况探究，再推广到一般情况． 21. 函数 f(x)(x2)ex ax2 2ax，aR． （1）当a0时，证明： f xe0； （2）若x1是 f x 的一个极大值点，求实数a的取值范围． 【答案】（1）证明见解析 e  （2） ,  2  【解析】 【分析】（1）当a0时求出函数解析式，即可求出导函数，从而求出函数的单调性，即可得到函数的最小 值，即可得证； （2）求出函数的导函数 f(x)x1 ex 2a  ，分a0、a e 、0a e 、a  e 四种情况讨论， 2 2 2 分别求出函数的单调性，即可得到函数的极值点，即可得解. 【小问1详解】 当a0时 f(x)(x2)ex，则 f(x)(x1)ex， 所以当x1时 f(x)0，当x1时 f(x)0， 第14页/共17页 学科网（北京）股份有限公司所以 f x 的单调递增区间为 1, ，单调递减区间为 ,1 ， 所以 f x 在x1处取得极小值即最小值，即 f x  f 1e， min 所以 f xe0恒成立. 【小问2详解】 函数 f(x)(x2)ex ax2 2ax定义域为R ，且 f(x)(x1)ex 2ax2a x1 ex 2a  ， 当2a0，即a0时ex 2a 0恒成立， 当x1时 f(x)0，当x1时 f(x)0， 所以 f x 的单调递增区间为 1, ，单调递减区间为 ,1 ， 所以 f x 在x1处取得极小值，即x1是 f x 的一个极小值点，不符合题意； e 当2a  e，即a 时 f(x)0恒成立，所以 f x 在R 上单调递增，无极值，不符合题意； 2 e 当02ae，即0a 时， 2 令 f¢(x)>0，解得xln2a或x1，令 fx0，解得ln2a x1， 所以 f x 在 ,ln2a ， 1, 上单调递增，在 ln2a,1 上单调递减， 所以 f x 在x1处取得极小值，即x1是 f x 的一个极小值点，不符合题意； e 当2a e，即a  时， 2 令 f¢(x)>0，解得x1或xln2a，令 fx0，解得1 xln2a， 所以 f x 在 ,1 ， ln2a, 上单调递增，在 1,ln2a 上单调递减， 所以 f x 在x1处取得极大值，即x1是 f x 的一个极大值点，符合题意； e  综上可得实数a的取值范围为 , . 2  （二）选考题：共 10分.请考生在第 22、23题中任选一题作答.如果多做，则按所做的第一 题计分. [坐标系与参数方程] x2cos, 22. 在平面直角坐标系xoy中，曲线C的参数方程为 （为参数）．以坐标原点为极点，x y 2sin 第15页/共17页 学科网（北京）股份有限公司π 轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为 (R)． 3 （1）求曲线C的极坐标方程； 1 1 （2）若直线l与曲线C交于M,N 两点，求  ． OM ON 【答案】（1）2 4(sincos)70 2( 31) （2） 7 【解析】 xcos 【分析】（1）先化参数方程为直角坐标方程，然后将 代入整理即可. y sin （2）联立直线和（1）中的极坐标方程，结合韦达定理求解. 【小问1详解】 x2cos 由 可得(x2)2 (y2)2 1， y 2sin xcos 将 代入可得，cos22 sin22 1， y sin 整理可得2 4(sincos)70，即为曲线C的极坐标方程. 【小问2详解】 π  (R)和2 4(sincos)70联立可得，2 2( 31)70， 3  2( 31) 设M,N 对应得极径分别为,，根据韦达定理， 1 2 ， 1 2   7 1 2 1 1 OM  ON  2( 31) 于是    1 2  OM ON OM ON  7 1 2 [不等式选讲] 23. 已知 f x x3,gx6 x1 ． （1）若 f xgx ，求x的取值范围； （2）若不等式 f xgx2a2 5a的解集为R ，求实数a的取值范围． 【答案】（1）{x∣x4或x£ -2} 第16页/共17页 学科网（北京）股份有限公司 1 （2）a 2a   2 【解析】 【分析】（1）由 f xgx 可得 x3  x1 6，分类讨论x3，1 x3，x1三种情况，将 原不等式转化为不含绝对值的不等式求解即可； （2）根据题意得到 f(x)g(x)2，从而得到关于a的二次不等式，再由一元二次不等式解法，即可求 出结果. 【小问1详解】 由 f xgx 可得 x3  x1 6， 当x3时，原不等式可化为2x26，解得x4； 当1 x3时，原不等式可化为46，显然不成立； 当x1时，原不等式可化为22x6，解得x2； 所以x的取值范围为{x∣x4或x£ -2}； 【小问2详解】 因为 f xgx x3  x16 3xx162，当且仅当1 x3时等号成立， 1 所以由不等式 f xgx2a2 5a的解集为R ，可得2a2 5a20，解得2a ． 2  1 故实数a的取值范围是a 2a ．  2 第17页/共17页 学科网（北京）股份有限公司