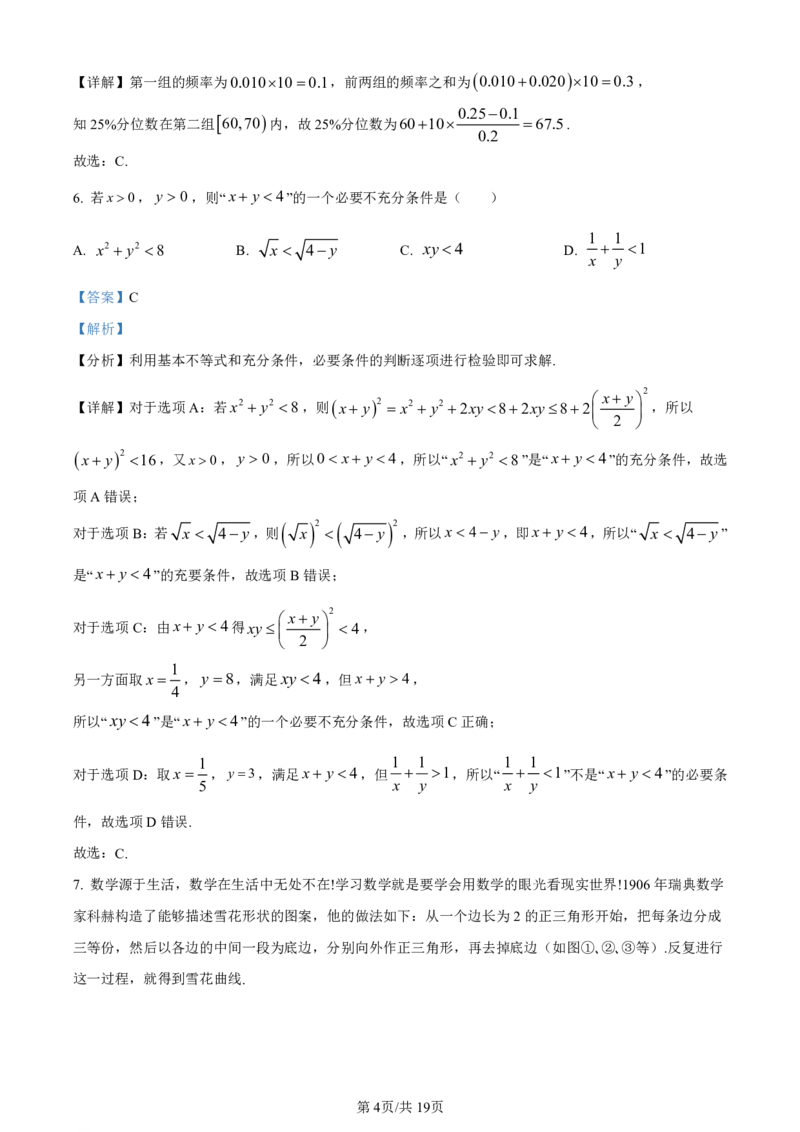黑龙江省牡丹江市第二高级中学2023-2024学年高三上学期第二次阶段性考试数学答案(1)_2023年10月_01每日更新_22号_2024届黑龙江省牡丹江市第二高级中学高三上学期第二次阶段性考试

牡丹江二中 2023-2024 学年度第一学期高三第二次阶段性考试 数学 考生注意： 1.本试卷满分 150分，考试时间 120分钟. 2.答题前，考生务必用直径 0.5毫米黑色，墨水签字笔将密封线内项目填写清楚. 3.考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B 铅笔把答题卡上对应 题目的答案标号涂黑；非选择题请用直径 0.5毫米，黑色，墨水签字笔在答题卡上各题的答题 区域内作答，超出答题区域书写的答案无效，在试题卷､草稿纸上作答无效. 4.本卷命题范围：集合与逻辑､不等式､函数与导数､三角函数､数列､统计. 一､选择题：本大题共 8小题；每小题 5分，共 40分.在每小题给出的四个选项中，只有一个 选项是符合题目要求的. 1. 已知集合 A  x x2x6 0  ， B   x x10  ，则 AB  （ ） A. 3, B. ,2  C. 3,1  D. 1,2  【答案】C 【解析】 【分析】先解不等式求出两集合，再求两集合的交集 【详解】由x2 x60，得(x2)(x3)0，解得3 x2，   所以A x 3 x2 ，   由x10，得x1，所以B  x x1 ，   所以AB  x 3 x1 ， 故选：C 1 2. 函数 f  x  1x  的定义域是（ ） x A. 1,0    0, B. 1, C. R D. ,0 U  0, 【答案】A 【解析】 【分析】根据开偶数次方根号里的数大于等于零，分母不等于零，即可得解. 1 【详解】解：由函数 f  x  1x  ， x 第1页/共19页 学科网（北京）股份有限公司1x0 得 ，解得x1且x0， x0 1 所以函数 f  x  1x  的定义域是 1,0    0, . x 故选：A. 3. 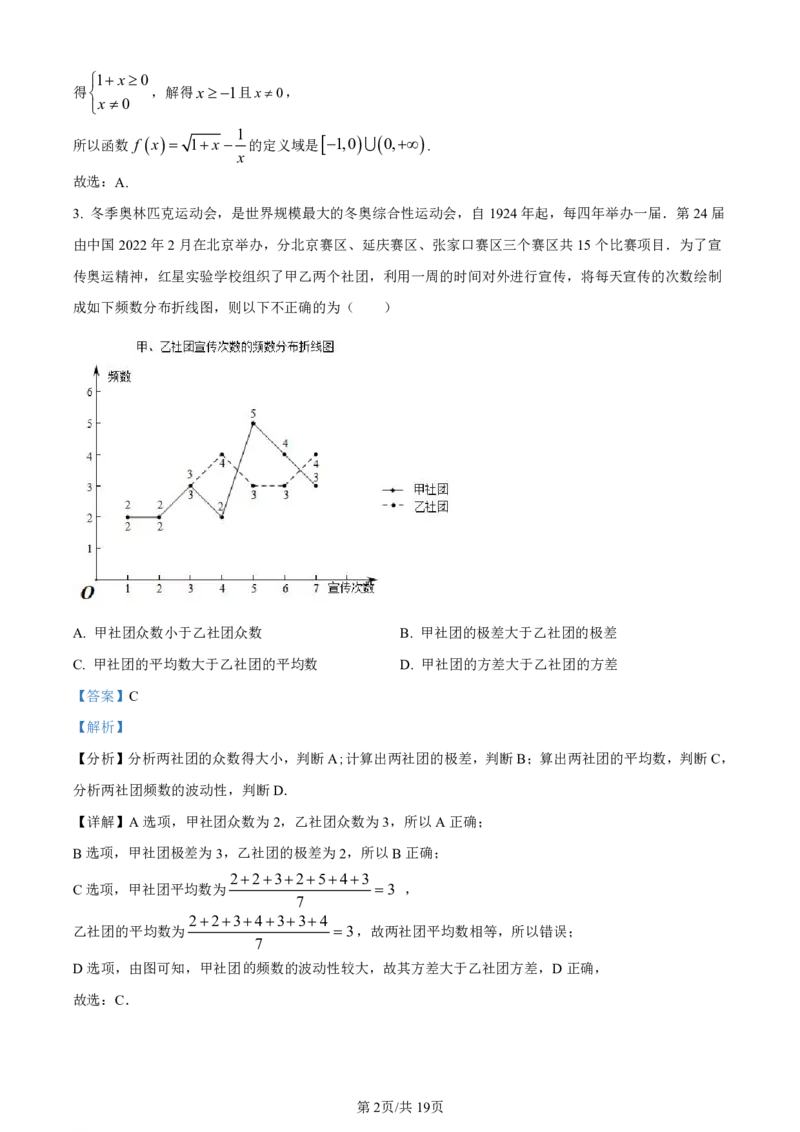冬季奥林匹克运动会，是世界规模最大的冬奥综合性运动会，自1924年起，每四年举办一届．第24届 由中国2022年2月在北京举办，分北京赛区、延庆赛区、张家口赛区三个赛区共15个比赛项目．为了宣 传奥运精神，红星实验学校组织了甲乙两个社团，利用一周的时间对外进行宣传，将每天宣传的次数绘制 成如下频数分布折线图，则以下不正确的为（ ） A. 甲社团众数小于乙社团众数 B. 甲社团的极差大于乙社团的极差 C. 甲社团的平均数大于乙社团的平均数 D. 甲社团的方差大于乙社团的方差 【答案】C 【解析】 【分析】分析两社团的众数得大小，判断A;计算出两社团的极差，判断B；算出两社团的平均数，判断C， 分析两社团频数的波动性，判断D. 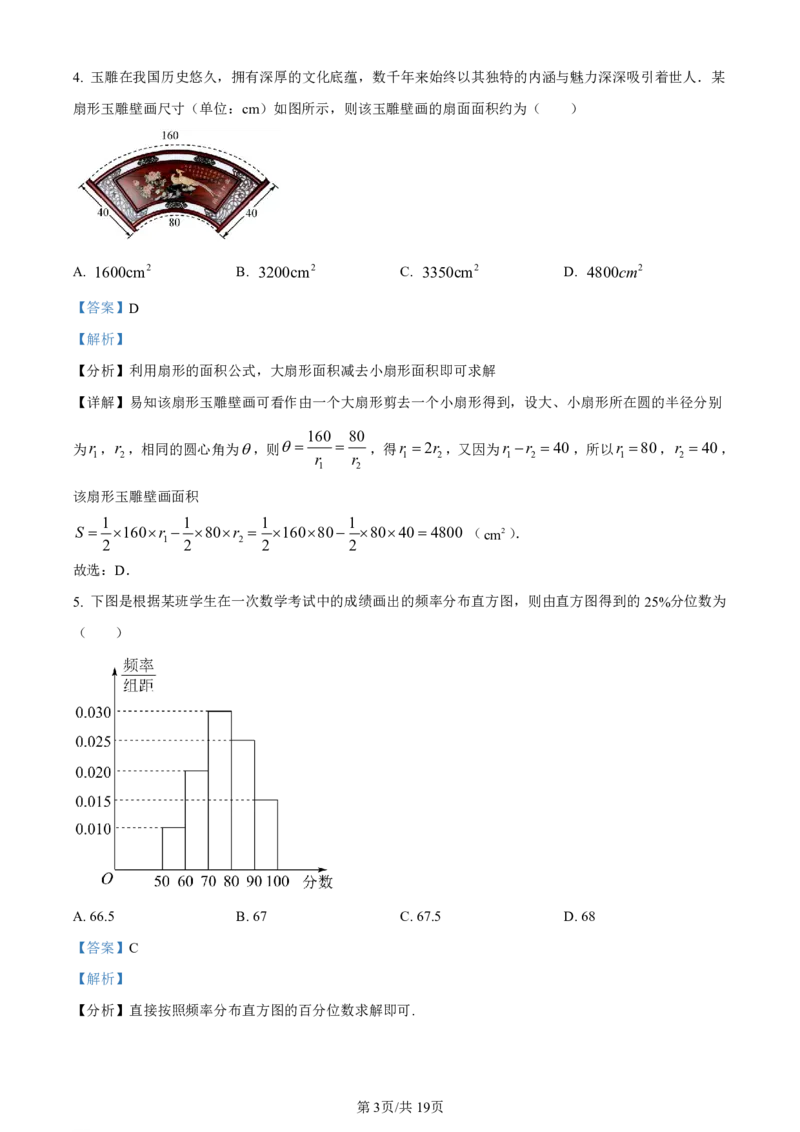【详解】A选项，甲社团众数为2，乙社团众数为3，所以A正确； B选项，甲社团极差为3，乙社团的极差为2，所以B正确； 2232543 C选项，甲社团平均数为 3 ， 7 2234334 乙社团的平均数为 3，故两社团平均数相等，所以错误； 7 D选项，由图可知，甲社团的频数的波动性较大，故其方差大于乙社团方差，D正确， 故选：C． 第2页/共19页 学科网（北京）股份有限公司4. 玉雕在我国历史悠久，拥有深厚的文化底蕴，数千年来始终以其独特的内涵与魅力深深吸引着世人．某 扇形玉雕壁画尺寸（单位：cm）如图所示，则该玉雕壁画的扇面面积约为（ ） A. 1600cm2 B. 3200cm2 C. 3350cm2 D. 4800cm2 【答案】D 【解析】 【分析】利用扇形的面积公式，大扇形面积减去小扇形面积即可求解 【详解】易知该扇形玉雕壁画可看作由一个大扇形剪去一个小扇形得到，设大、小扇形所在圆的半径分别 160 80 为r ，r ，相同的圆心角为，则  ，得r 2r ，又因为r r  40，所以r 80，r 40， 1 2 r r 1 2 1 2 1 2 1 2 该扇形玉雕壁画面积 1 1 1 1 S  160r  80r  16080 80404800 （cm2）． 2 1 2 2 2 2 故选：D． 5. 下图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图，则由直方图得到的25%分位数为 （ ） A.66.5 B.67 C.67.5 D.68 【答案】C 【解析】 【分析】直接按照频率分布直方图的百分位数求解即可. 第3页/共19页 学科网（北京）股份有限公司【详解】第一组的频率为0.010100.1，前两组的频率之和为  0.0100.020 100.3， 0.250.1 知25%分位数在第二组  60,70  内，故25%分位数为6010 67.5. 0.2 故选：C. 6. 若x0， y  0，则“x y4”的一个必要不充分条件是（ ） 1 1 A. x2  y2 8 B. x  4y C. xy4 D.  1 x y 【答案】C 【解析】 【分析】利用基本不等式和充分条件，必要条件的判断逐项进行检验即可求解.  x y 2 【详解】对于选项A：若x2  y2 8，则 x y 2  x2  y2 2xy82xy82  ，所以  2   x y 2 16，又x0，y  0，所以0 x y4，所以“x2  y2 8”是“x y4”的充分条件，故选 项A错误；  2  2 对于选项B：若 x  4 y，则 x  4 y ，所以x 4 y，即x y4，所以“ x  4 y” 是“x y4”的充要条件，故选项B错误；  x y 2 对于选项C：由x y4得xy   4，  2  1 另一方面取x ， y 8，满足xy4，但x y 4， 4 所以“xy4”是“x y4”的一个必要不充分条件，故选项C正确； 1 1 1 1 1 对于选项D：取x  ，y3，满足x y4，但  1，所以“  1”不是“x y4”的必要条 5 x y x y 件，故选项D错误. 故选：C. 7. 数学源于生活，数学在生活中无处不在!学习数学就是要学会用数学的眼光看现实世界!1906年瑞典数学 家科赫构造了能够描述雪花形状的图案，他的做法如下：从一个边长为2的正三角形开始，把每条边分成 三等份，然后以各边的中间一段为底边，分别向外作正三角形，再去掉底边（如图①､②､③等）.反复进行 这一过程，就得到雪花曲线. 第4页/共19页 学科网（北京）股份有限公司不妨记第n(n 1,2,3,)个图中的图形的周长为a ，则a （ ） n 5 256 256 512 512 A. B. C. D. 9 27 27 81 【答案】C 【解析】 【分析】根据题图规律确定第n个图边的条数及其边长，并写出其通项公式，再求第5个图的周长. 【详解】由图知：第一个图有3条边，各边长为2，故周长a 32； 1 2 2 第二个图有12条边，各边长为 ，故周长a 12 ； 3 2 3 2 2 第三个图有48条边，各边长为 ，故周长a 48 ； 9 3 9 …… 所以边的条数是首项为3，公比为4的等比数列，则第n个图的边有34n1条， 1 1 边长是首项为2，公比为 的等比数列，则第n个图的边长为2( )n1， 3 3 1 512 故a 3442( )4  5 3 27 . 故选：C 1 8. 设函数 f(x)的定义域为[0,3)，满足 f(x1)2f(x) ，且当x[0,1)时， f(x)x(1x).则不等式 4 5 f(x) 的解集是（ ）公众号：高中试卷君 8 5 7 4 5 5 7 4 5 A.  ,  [2,3) B.  ,  [2,3) C.  ,  (2,3) D.  ,  (2,3) 4 4 3 3 4 4 3 3 【答案】A 【解析】 【分析】分x[0,1)，x[1,2)和x[2,3)进行分类讨论，即可求解 第5页/共19页 学科网（北京）股份有限公司5 【详解】当x[0,1)， f(x) x(1x) ，解得x无实数解； 8 1 1 1 当x[1,2)，x1[0,1)，则由 f(x1)2f(x) 可得 f(x)2f(x1) 2(x1)(2x) ， 4 4 4 1 5 令2(x1)(2x)  ，整理得16x2 48x350，解得 4 8 5 7 解得  x ， 4 4 1 当x[2,3)，x1[1,2)，则由 f(x1)2f(x) 可得 4 2 1  1 1 3  5 7 f(x)2f(x1) 2  2(x2)(3x)   4(x2)(3x) 4 x   ， 4  4 4 4  2 4 3 7 5 因为x[2,3)，所以 f(x) , ，所以 f(x) 恒成立，   4 4 8 5 5 7 综上所述，不等式 f(x) 的解集是 , [2,3)   8 4 4 故选：A 二､多选题：本大题共 4小题，每小题 5分，共 20分.在每小题给出的选项中，有多项符合题 目要求.全部选对的得5分，部分选对的得 2分，有选错的得 0分. 9. 下列命题正确的是 A. a,bR, a2 (b1)20 B. aR，xR ，使得ax2 a b C. ab0是a2 b2 0的充要条件 D. a≥b1，则  1a 1b 【答案】AD 【解析】 【分析】对A．当a 2,b1时，可判断真假，对B. 当a 0时，0x=02，可判断真假，对C. 当 a 0,b0时，可判断真假，对D可用作差法判断真假. 【详解】A．当a 2,b1时，不等式成立，所以A正确. B. 当a 0时，0x=02，不等式不成立，所以B不正确. C. 当a 0,b0时，a2 b2 0成立，此时ab=0，推不出ab0.所以C不正确. a b a(1b)b(1a) a b a b D. 由    ，因为a≥b1，则  ,所以D正确. 1a 1b (1a)(1b) (1a)(1b) 1a 1b 故选：AD. 第6页/共19页 学科网（北京）股份有限公司本题考查命题真假的判断，充要条件的判断，作差法比较大小，属于中档题. 10. 已知等差数列  a  的前n项和为S ，满足a a a 21，S 25，下列说法正确的是（ ） n n 1 2 3 5 A. a 2n3 B. S n2 10n n n  1  10 C.  S  的最大值为S D.  的前10项和为 n 5 a a  99 n n1 【答案】BCD 【解析】公众号：高中试卷君   【分析】先根据题干条件算出等差数列 a 的通项公式，然后逐一分析每个选项即可. n 【详解】根据等差中项，a a a  213a ，解得a 7， 1 2 3 2 2 S 25a a a a a a   a a   a a 5a ，解得a 5，设等差数列  a  的公差为d， 5 1 2 3 4 5 3 1 5 2 4 3 3 n 则d a a 2，于是等差数列的通项公式为：a a (n2)d 112n ，故A选项错误； 3 2 n 2 n(a a ) n(9112n) 根据等差数列前n项和公式，S  1 n  n210n，B选项正确； n 2 2 根据B选项可知，S n2 10n(n5)2 25 25，最大值在n5取得，故C选项正确； n 1 1 1 1  1 1   1       ，故 的前10项和为： a a (112n)(92n) (2n11)(2n9) 2 2n11 2n9  a a  n n1 n n1 1 1  1  1  1 1 1  1 1 1  10                         ，D选项正确. 2 9  7  7  5 9 11 2 9 11 99 故选：BCD 11. 已知函数 f  x  的定义域为R ，且 f  0 0．若 y  f  x2 1为奇函数， y  f  x4  为偶函数， 则（ ） A. f  4 0 B. f 80 C. f  1  f  3 2 D. f 1 f 7 【答案】BD 【解析】 【分析】根据函数的奇偶性得到 f  x2  f x2 20， f  x4  f x4  ，取x2，x4， x 1，x3代入计算得到答案. 第7页/共19页 学科网（北京）股份有限公司【详解】y  f  x2 1为奇函数，故 f  x2 1f x2 1，即 f  x2  f x2 20， y  f  x4  为偶函数，即 f  x4  f x4  . 取x2得到 f  22  f 22 20，故 f  4 2，A错误； 取x4得到 f  44  f 44  f  0 0，B正确； 取x 1得到 f  12  f 12 20，即 f  3  f  1 2，C错误； 取x3得到 f  34  f 34  ，即 f 1 f 7，D正确. 故选：BD 12. 对于三次函数 f  x ax3bx2 cxd  a0  ，给出定义： f  x  是函数y f  x  的导数， f x  是函数 f  x  的导数，若方程 f x 0有实数解x ，则称  x , f  x  为函数 y f  x  的“拐点”.某同学 0 0 0 经探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.若 2 49 函数 f  x  x3x2 12x ，则下列说法正确的是（ ） 3 6 137   A. f x 的极大值为 6   B. f x 有且仅有2个零点 1  C. 点 ,2是 f  x  的对称中心 2   1   2   3  2023 D. f    f    f   f    4046 2024 2024 2024 2024 【答案】ACD 【解析】 【分析】求得 f x 2(x3)(x2)，得出函数单调性，结合极值的概念，可判定A正确；根据极大值为 f 2 0，极小值 f  3 0，进而得到函数 f  x  有3个零点，可判定B错误；求得 f x 4x2， 1 1 令 f x 0，求得x ，得出 f( )2，可判定C正确；根据对称性，得到 f  x  f(1x)4，结 2 2 合倒序相加法，可判定D正确. 2 49 【详解】由函数 f  x  x3x2 12x ，可得 f x 2x2 2x122(x3)(x2)， 3 6 第8页/共19页 学科网（北京）股份有限公司令 f ¢( x )>0，解得x<2或x 3；令 fx0，解得2 x3， 所以函数 f  x  在(,2)上单调递增，在(2,3)上单调递减，在(3,)单调递增， 137 当x2时， f  x  取得极大值，极大值为 f 2  ，所以A正确； 6 113 又由极小值 f  3  0，且当x时， f  x ， 6 当x时， f  x ，所以函数 f  x  有3个零点，所以B错误； 1 由 f x 2x2 2x12，可得 f x 4x2，令 f x 0，可得x ， 2 1 2 1 1 1 49 1  又由 f( ) ( )3 ( )2 12  2，所以点 ,2是函数 f  x  的对称中心， 2 3 2 2 2 6 2  所以C正确； 1  因为 ,2是函数 f  x  的对称中心，所以 f  x  f(1x)4， 2   1   2   3  2023 令S  f    f    f    f  ， 2024 2024 2024 2024 2023 2022  2021  1  可得S  f    f    f    f  ， 2024 2024 2024 2024 所以  1  2023  2  2022  3  2021 2S [f    f  ][f    f  ][f    f  ] 2024 2024 2024 2024 2024 2024 2023  1  [f    f  ] 42023， 2024 2024  1   2   3  2023 所以S 4046，即 f    f    f   f    4046， 2024 2024 2024 2024 所以D正确. 故选：ACD. 三､填空题：本大题共 4小题，每小题 5分，共 20分. 1  13. 若sinx ，则cos(x )___________. 3 2 1 【答案】 3 第9页/共19页 学科网（北京）股份有限公司【解析】 【分析】 由题意利用利用诱导公式化简要求的式子，可得结果．  1 【详解】由诱导公式可得cos(x )sinx 2 3 1 故答案为： 3 14. 将某射击运动员的十次射击成绩（环数）按从小到大的顺序（相等数据相邻排列）排列为：8.1，8.4， 1 1 8.4，8.7，x，y，9.3，9.4，9.8，9.9，已知总体的中位数为9，则  的最小值为__________． x y 2 【答案】 9 【解析】 【分析】由中位数的概念结合基本不等式可得. 【详解】因为总体的中位数为9．所以x y 18，则 1 1 1 1 1  1  x y 1  x y  2       x y  2   ≥   22     ，当且仅当x y 9时等号成立． x y 18x y  18 y x  18  y x  9 2 故答案为： 9 1 15. 已知 f   2f x 3x，x0，则 f  x  的解析式为________．  x 1 【答案】2x x 【解析】 1 1 3 【分析】将 代入条件中，得到 f x 2f    ，根据两式消元，求得函数 f  x  的解析式. x  x x 1 3 1 【详解】由题知， f x 2f    ，①；又 f   2f x 3x，②；  x x  x 1 由①2②得， f(x) 2x， x 1 则 f  x 2x ， x 1 故答案为：2x x 1 1 16. 若曲线yln(xa)的一条切线为 y exb（e为自然对数的底数），其中a,b为正实数，则  的 ea b 第10页/共19页 学科网（北京）股份有限公司取值范围是_________ 【答案】[2,) 【解析】 【分析】根据导数的几何意义及切线方程可得eab2，由“1”的技巧及均值不等式求解即可. 1 【详解】∵ yln(xa)，∴ y ， xa ln  x +a  =ex b  0 0   设切点为 x ,y ，则 1 ， 0 0 =e  x +a 0 1 1 1 1 1 1 b ea ∴eab2，∴     (eab) 2   ． ea b 2ea b 2 ea b  ∵a,b,e0， 1 b ea  b ea 1 ∴原式 2  2，当且仅当  ，即a  ,b1时等号成立，   2 ea b  ea b e 1 1 即   2． ea b 故答案为：[2,) 四､解答题：本大题共 6小题，共 70分.解答应写出必要的文字说明､证明过程及演算步骤. 17. 已知在递增的等差数列  a  中，a a 55，a a 16． n 3 7 4 6 （1）求a 和a ； 3 7   （2）求 a 的通项公式． n 【答案】（1）a 5,a 11 3 7 3 1 （2）a  n n 2 2 【解析】 a a 55 【分析】（1）由a a a a 16，结合题意得到方程组 3 7 ，即可求解； 4 6 3 7 a a 16 3 7 （2）设数列  a  的公差为d，由（1）列出方程组，求得a ,d 的值，即可求解. n 1 【小问1详解】 第11页/共19页 学科网（北京）股份有限公司a a 55 解：因为a a a a 16，所以 3 7 ， 4 6 3 7 a a 16 3 7 解得a 5,a 11或a 11,a 5， 3 7 3 7 又因为数列  a  递增数列，所以a 5,a 11. n 3 7 【小问2详解】 解：设数列  a  的公差为d（d 0）， n a 2d 5 3 由a 5,a 11，可得 1 ，解得a 2，d  ， 3 7 a 6d 11 1 2 1 3 1 所以数列  a  的通项公式为a a  n1  d  n ． n n 1 2 2 18.2021年，为降低疫情传播风险，保障经济社会良好运行，各地区鼓励外来务工人员就地过节、过年．某 市统计了该市4个地区的外来务工人员数与就地过年的人员数，得到如下的表格： A区 B区 C区 D区 外来务工人员数x/万人 3 4 5 6 就地过年的人员数 y /万人 2.5 3 4 4.5 （1）已知可用线性回归模型拟合 y与x的关系，求 y关于x的线性回归方程 yˆ b ˆ xaˆ． （2）假设该市政府对外来务工人员中选择就地过年的人每人发放1000元补贴．若该市E区有2万名外来 务工人员，根据（1）的结论估计该市政府需要给E区选择就地过年的人员发放的补贴总金额； n n x y nxy  x x  y y  i i i i 参考公式：回归方程 yˆ b ˆ xaˆ 中斜率和截距的公式分别为b ˆ i1  i1 ， n n x2 nx2  x x 2 i i i1 i1 aˆ  yb ˆ x． 【答案】（1） yˆ 0.7x0.35 （2）1750（万元） 【解析】 【分析】（1）利用公式求出b ˆ0.7和aˆ 0.35，得到线性回归方程； 第12页/共19页 学科网（北京）股份有限公司（2）在第一问的基础上，代入x=2求出 yˆ 1.75，从而估计该市政府需给E区选择就地过年的人员发放补 贴总金额. 【小问1详解】 3456 2.5344.5 x  4.5， y   3.5， 4 4 4 4 x y 32.5435464.566.5， x2 32 42 52 62 86， i i i i1 i1 66.544.53.5 所以，b ˆ 0.7，则aˆ  yb ˆ x 3.50.74.50.35， 8644.52 故 y关于x的线性回归方程为 yˆ 0.7x0.35； 【小问2详解】 将x=2代入 yˆ 0.7x0.35得： yˆ 0.720.351.75， 估计该市政府需给E区选择就地过年的人员发放补贴总金额为1.7510001750（万元）.   2 7   1   19. 已知cos     ，sin    ， ，0 ，求：  2  7  2  2 2 2  （1）cos 的值； 2 （2）tan  的值. 21 【答案】（1） 14 5 3 （2） 11 【解析】   【分析】（1）先由已知条件判断 , 的范围，再利用同角三角函数的关系求出 2 2          sin  ,cos  ，则由cos cos       利用两角差的余弦公式可求得  2   2  2  2   2   cos ， 2   （2）由同角三角函数的关系求出sin ，从而可求得tan 的值，再利用正切的二倍角公式可求 2 2 得tan  的值. 【小问1详解】 第13页/共19页 学科网（北京）股份有限公司  因为 ，0 ， 2 2      所以  ，   ， 4 2 4 2 2     21 所以sin    1cos2     ，  2   2  7     3 cos    1sin2     ，  2   2  2      所以cos cos       2  2   2          cos  cos   sin  .sin    2   2   2   2  2 7 3 21 1 21      . 7 2 7 2 14 【小问2详解】   3  21 因为   ，cos  ， 4 2 4 2 14   5 7 所以sin  1cos2  ， 2 2 14  sin  2 5 3 所以tan   ， 2  3 cos 2  5 3  2  2tan 2  3  5 3 所以tan()   . 1tan2   5 3 2 11 2 1   3  20. 设函数 f  x axlnx，其中aR，曲线y f  x  在点  1, f  1  处的切线经过点  3,2  .   （1）求函数 f x 的极值； x 2 （2）证明： f x  . ex e 1 【答案】（1）极小值为 ，没有极大值 e （2）证明见解析 第14页/共19页 学科网（北京）股份有限公司【解析】 1 【分析】（1）先解出a，代入函数解析式，求导即可求解（2）由（1）可得 f xxlnx ，可将所要证 e 1 x 明的不等式转化为  0(需验证等号不同时成立)，构造函数，求导，研究其最值即可证明 e ex 【小问1详解】 fxalnxa，则 f  1 0， f 1 a， 故 y f  x  在  1, f  1  处的切线方程 ya  x1  ，   把点 3,2 代入切线方程可得，a 1， f x lnx1，x0， 1 易得，当0 x 时， fx0，函数单调递减， e 1 当x  时， f ¢( x )>0，函数单调递增， e 1 1 1 故当x  时，函数取得极小值 f    ，没有极大值. e e e 【小问2详解】 x 2 x 2 证明： f x  等价于xlnx  0， ex e ex e 1 1 由（1）可得 f xxlnx (当且仅当x  时等号成立)①， e e x 2 1 x 所以xlnx    ， ex e e ex 1 x 故只要证明  0即可，(需验证等号不同时成立) e ex 1 x x1 设gx  ，x0则gx ， e ex ex 当0 x 1时，g x 0，函数单调递减，当x1时，g x 0，函数单调递增， 所以g  x  g  1 0，当且仅当x 1时等号成立，② 因为①②等号不同时成立， x 2 所以当x0时， f x  . ex e 21. 已知数列  a  的前n项和为S ，满足S 2n2a · n n n n （1）证明：数列  a 2  是等比数列，并求数列  a  的通项公式； n n 第15页/共19页 学科网（北京）股份有限公司 b  3 （2）若b log  a 2  ，设T 是数列 n 的前n项和，求证：T  . n 2 n n a 2 n 2 n 【答案】（1）证明见解析，a 2n12； n （2）证明见解析. 【解析】 【分析】（1）利用a 与S 关系可推导得到a 22  a 2  ，由此可证得数列  a 2  为等比数列，结 n n n n1 n 合等比数列通项公式求得a 2后可推导得到a ； n n b 3 n3 n3 （2）由（1）可得 n ，采用错位相减法可求得T   ，由 0可得结论. a 2 n 2 2n1 2n1 n 【小问1详解】 由S 2n2a 得：S 2a 2n； n n n n 当n 1时，S 2a 2，解得：a 2； 1 1 1 当n2且nN*时，S 2a 2  n1  ， n1 n1 a  S S  2a 2a 2n2  n1  ，即a 2a 2，a 22  a 2  ， n n n1 n n1 n n1 n n1 数列  a 2  是以a 24为首项，2为公比的等比数列； n 1 a 242n1 2n1，a 2n12. n n 【小问2详解】 b n1 由（1）得：b log 2n1 n1， n  ， n 2 a 2 2n1 n 2 3 4 n n1 1 2 3 4 n n1 T      ， T      ， n 22 23 24 2n 2n1 2 n 23 24 25 2n1 2n2 两式作差得： 1  1  1  1 1 n1  1 1 1  1 n1 23  2n1 1 n1 1  1  T              1  2 n 2 2n2 23 24 2n1  2 2n2 1 2 2n2 22  2n1  1 2 1 n1 1 1 3 n3       ， 2 2n2 4 2n1 4 2n2 3 n3 n3 3 T   ，又 0，T  . n 2 2n1 2n1 n 2 第16页/共19页 学科网（北京）股份有限公司1 22. 已知 f(x)ex  ax2 b(x1).其中常数e2.71828. 2 （1）当a 2,b4时，求 f(x)在[1,2]上的最大值； （2）若对任意a0, f(x)均有两个极值点x ,x  x  x  ， 1 2 1 2 （ⅰ）求实数b的取值范围； （ⅱ）当a e时，证明： f  x  f  x e. 1 2 【答案】（1） f(x) e1；（2）（ⅰ）b1；（ⅱ）证明见解析. max 【解析】 【分析】 （1）由题得 f(x)ex x24(x1)，f(x)ex 2x4，f(x)ex 2，由x[1,2]，可得 f(x)0， 即 f(x)在[1,2]上单增，且 f(2) e2 80，即 f(x)0，可知 f(x)在[1,2]上单减，求得 f(x)  f(1)e1. max （2）（ⅰ）利用两次求导可得x(,lna)时， f(x)单减； x(lna,)时， f(x)单增，再由 f(x)有 两个极值点，知 f(lna)aalnab0，即baalna恒成立，构造函数g(a)aalna，利用 导数求其最大值，可得实数b的取值范围； （ⅱ）设h(x) f(x) f(2x),(x1)，求导可得h(x)在(,1)单增，得到 f(x) f(2x)，可得 f x  f 2x  ，f 2x  f x  ，结合 f(x)在(1,)上单增，可得 f  x  f  2x  ，得到 1 1 1 2 1 2 f  x  f  x  f  2x  f  x ex 2 e2x 2 ex2 2ex 2e，构造 1 2 2 2 2 2 M(x)ex e2x ex22ex2e ，(x1)，再利用导数证明M  x M(1)e，即可得到 2 f  x  f  x e 1 2 【详解】（1）由a 2,b4得， f(x)ex x24(x1)， 求导 f(x)ex 2x4， f(x)ex 2， x[1,2]，ex[e,e2]，ex 20，即 f(x)0  f(x)在[1,2]上单增，且 f(2) e2 80， 第17页/共19页 学科网（北京）股份有限公司即x[1,2]， f(x)0， f(x)在[1,2]上单减，  f(x)  f(1)e1. max （2）（ⅰ）求导 f(x)ex axb， 因为对任意a0, f(x)均有两个极值点x,x ，所以 f(x)0有两个根， 1 2 求二阶导 f(x)ex a，令 f(x)0，得xlna 当x(,lna)时， f(x)0， f(x)单减；当x(lna,)时， f(x)0， f(x)单增， 由 f(x)0有两个根x,x ，知 f(lna)aalnab0， 1 2 即baalna对任意a0都成立，设g(a)aalna，求导g(a)lna， 令g(a)0，得a 1， 当x(0,1)时，g(a)0，g(a)单增；当x(1,)时，g(a)0，g(a)单减， g(a)  g(1)1，b1 max  b  b 又Q f    e a  0,x, f(x) ，  a 所以实数b的取值范围是：b1. （ⅱ）当a e时， f(x) ex exb ， f(x)ex e， 令 f(x)0，得x 1 当x(,1)时， f(x)0， f(x)单减；当x(1,)时， f(x)0， f(x)单增， 又x,x 是 f(x)0的两根，且x  x ， 1 2 1 2 x 1, x 1，2x 1 1 2 1 设h(x) f(x) f(2x),(x1)， 即h(x)ex exbe2x e(2x)bex e2x 2ex2e,(x 1)，   则h(x) ex e2x 2e 2e2e 0 h(x)在(,1)单增，h(x)h(1)0，即 f(x) f(2x) 又x 1,， f x  f 2x  ， f 2x  f x  1 1 1 1 2 第18页/共19页 学科网（北京）股份有限公司又 f(x)在(1,)上单增， 2x  x ，即x 2x  x ， 1 2 1 2 2 又 f(x)在  x ,x  上单减， f  x  f  2x  1 2 1 2  f  x  f  x  f  2x  f  x ex 2e2x 2ex2 2ex 2e 1 2 2 2 2 2 令M(x)ex e2x ex22ex2e ，(x1) 则M(x)ex e2x 2ex2e ，M(x)ex e2x 2e0 M(x)在(1,)单增，且M(1)  0， M(x)0，故M(x)在(1,)单增 又x 1，M  x  M(1)e，即 f  x  f  x e 2 2 1 2 【点睛】方法点睛：本题考查利用导数研究函数的单调性，求极值，最值，以及证明不等式，证明不等式 的方法：若证明 f  x g  x  ，x(a,b)，可以构造函数F  x  f  x －g  x  ，如果F x 0，则F  x  在(a,b)上是减函数，同时若F  a 0，由减函数的定义可知x(a,b)时，有F  x 0，即证明了 f  x g  x  ，考查学生的函数与方程思想，化归与转化思想，考查逻辑思维能力与推理论证能力，属于 难题. 第19页/共19页 学科网（北京）股份有限公司