文档内容
五年(2019-2023)年高考真题分项汇编
专题 13 不等式
不等式作为高考一个工具,主要题型是小题,再者就是与其他知识点相结合。
考点01 解基本不等式
考点02 不等式应用—线性规划
考点04 不等式综合应用
考点 01:解基本不等式
一 填空题
1.(2021高考天津)若 ,则 的最小值为____________.
【答案】
【解析】: , ,
当且仅当 且 ,即 时等号成立, 所以 的最小值为 .
故答案 为: .
2.(2020天津高考·)已知 ,且 ,则 的最小值为_________.
【答案】4
【解析】 , ,
,当且仅当 =4时取等号,
结合 ,解得 ,或 时,等号成立.
故答案为:
3.(2020江苏高考·)已知 ,则 的最小值是_______.
【答案】
1【解析】 , 且
,当且仅当 ,即 时取等
号.
的最小值为 .故答案为: .
4.(2019·天津·理)设 ,则 的最小值为 .
【答案】 【解析】: ,
,当且仅当 即
或 时等号成立,因为 ,所以 ,故 的最小值为 .
5.(2019·上海)若 ,且 ,则 的最大值为________.
【答案】 【解析】法一: ,∴ ;
法二:由 , ( ),求二次最值 .
6.(2019·江苏·)在平面直角坐标系 中, 是曲线 上一动点,则点 到直线
的距离最小值是______.
【答案】4
【解析】法1:由已知,可设 ,所以 .
当且仅当 ,即 时取等号,故点 到直线的距离的最小值为4.
法2:距离最小时, ,则 ,所以 ,所以最小值为4.
7.(2022年全国高考甲卷数学(文)·)已知 中,点D在边BC上, .当
2取得最小值时, ________.
【答案】 或
【解析】设 ,
则在 中, ,
在 中, ,
所以
,
当且仅当 即 时,等号成立,
所以当 取最小值时, .故答案为: .
考点03:不等式应用—线性规划
一 单选题
31.(2021年高考浙江卷·)若实数x,y满足约束条件 ,则 的最小值是 ( )
A. B. C. D.
【答案】B
【解析】:画出满足约束条件 的可行域,如下图所示:
目标函数 化为 ,由 ,解得 ,设 ,当直线
过 点时, 取得最小值为 ,故选B.
2.(2021年全国高考乙卷文科·)若 满足约束条件 则 的最小值为 ( )
A.18 B.10 C.6 D.4
【答案】C
【解析】:由题意,作出可行域,如图阴影部分所示,
4由 可得点 ,
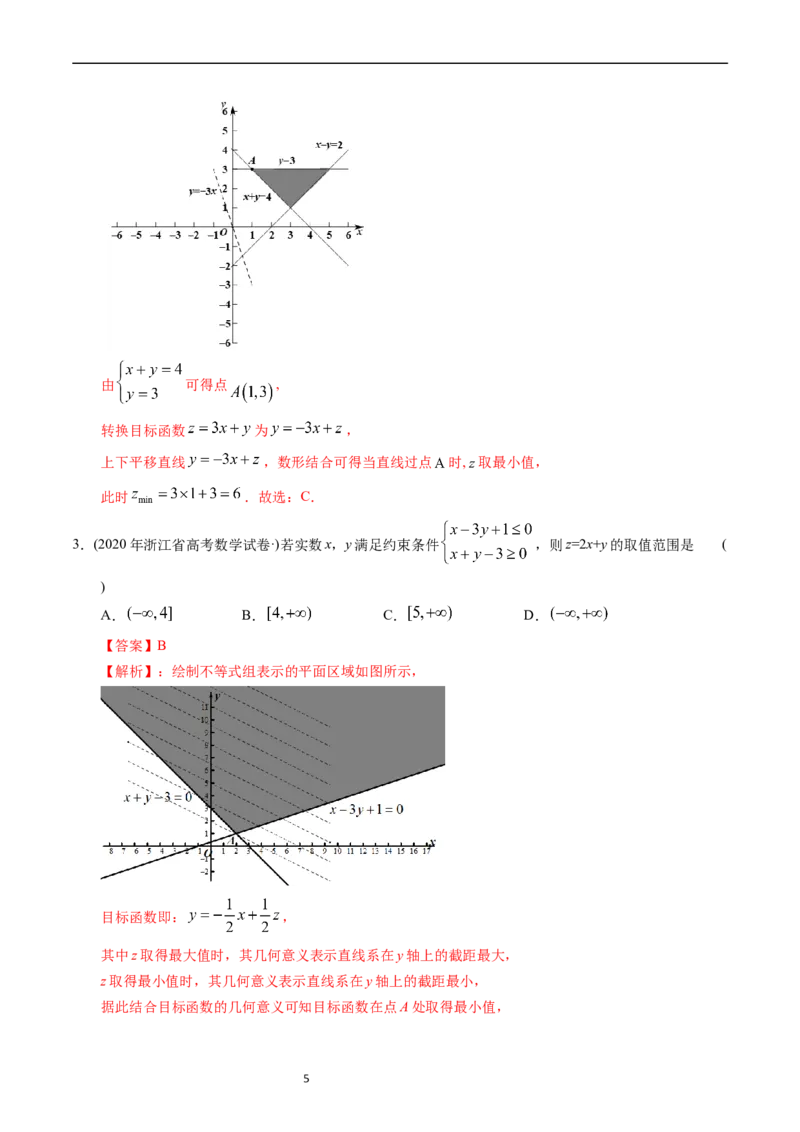
转换目标函数 为 ,
上下平移直线 ,数形结合可得当直线过点 时, 取最小值,
此时 .故选:C.
3.(2020年浙江省高考数学试卷·)若实数x,y满足约束条件 ,则z=2x+y的取值范围是 (
)
A. B. C. D.
【答案】B
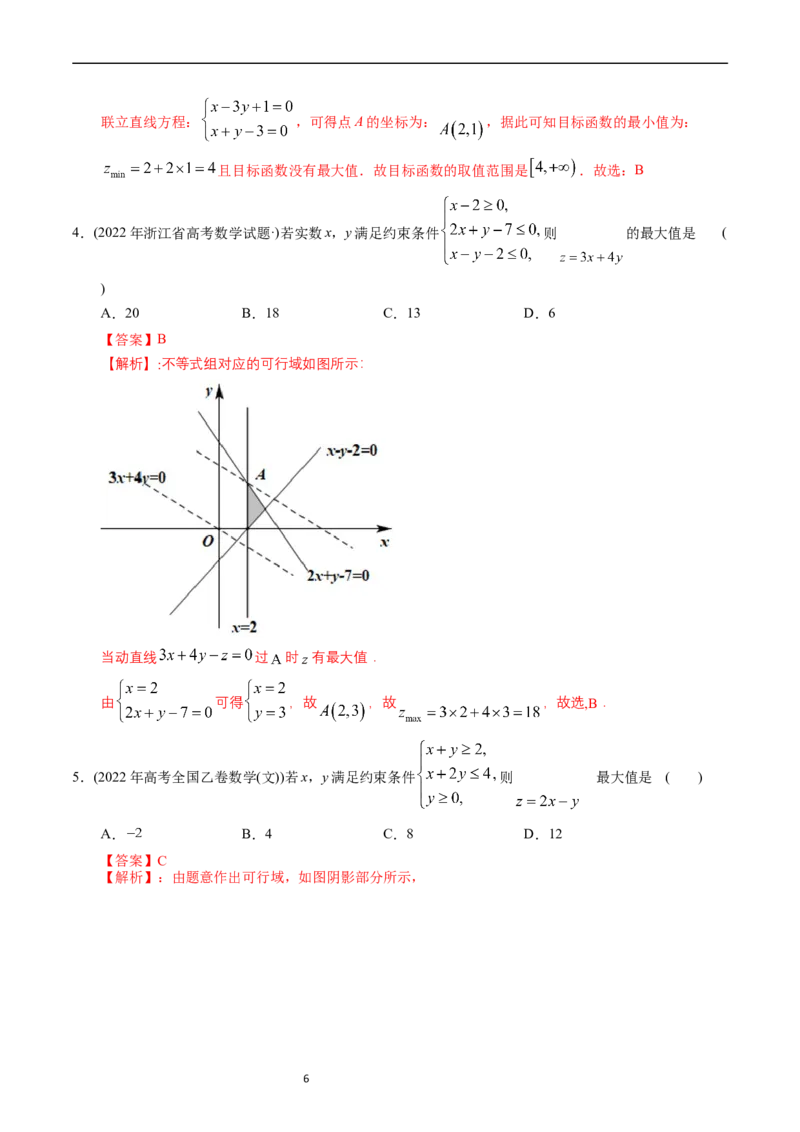
【解析】:绘制不等式组表示的平面区域如图所示,
目标函数即: ,
其中z取得最大值时,其几何意义表示直线系在y轴上的截距最大,
z取得最小值时,其几何意义表示直线系在y轴上的截距最小,
据此结合目标函数的几何意义可知目标函数在点A处取得最小值,
5联立直线方程: ,可得点A的坐标为: ,据此可知目标函数的最小值为:
.
且目标函数没有最大值.故目标函数的取值范围是 .故选:B
4.(2022年浙江省高考数学试题·)若实数x,y满足约束条件 则 的最大值是 (
)
A.20 B.18 C.13 D.6
【答案】B
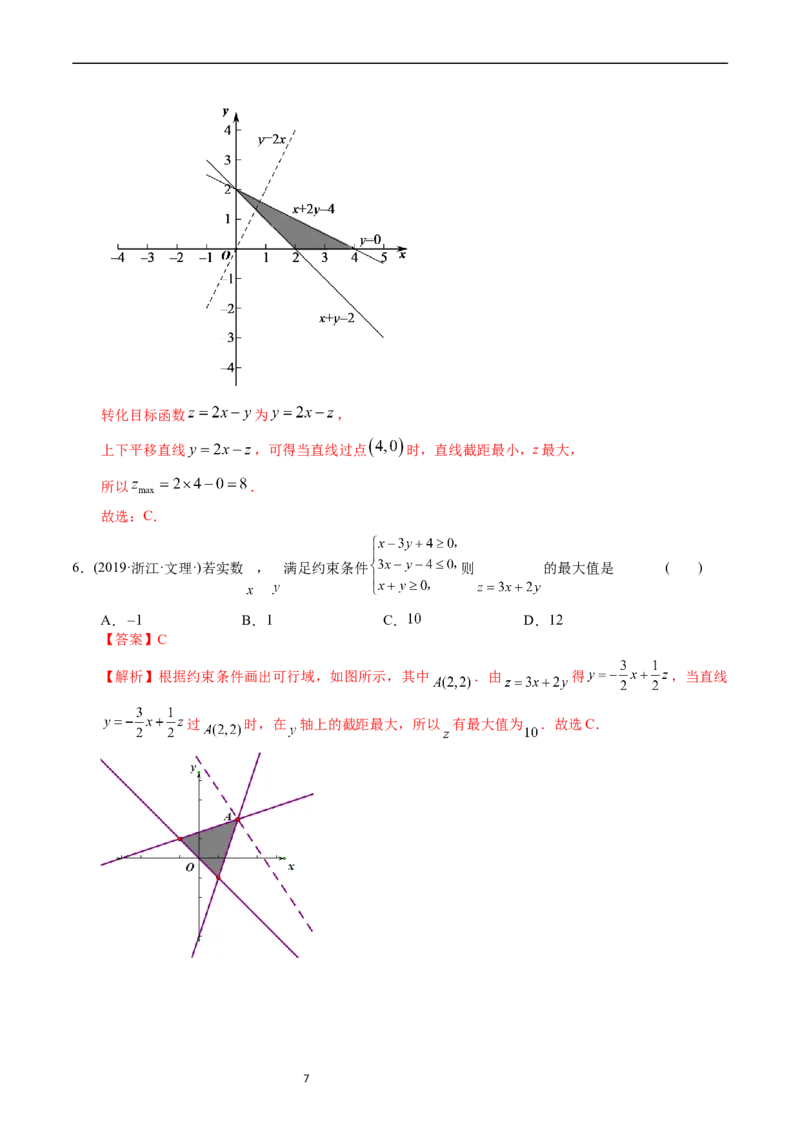
【解析】:不等式组对应的可行域如图所示:
当动直线 过 时 有最大值.
由 可得 ,故 ,故 ,故选,B.
5.(2022年高考全国乙卷数学(文))若x,y满足约束条件 则 最大值是 ( )
的
A. B.4 C.8 D.12
【答案】C
【解析】:由题意作出可行域,如图阴影部分所示,
6转化目标函数 为 ,
上下平移直线 ,可得当直线过点 时,直线截距最小,z最大,
所以 .
故选:C.
6.(2019·浙江·文理·)若实数 , 满足约束条件 则 的最大值是 ( )
A. B. C. D.
【答案】C
【解析】根据约束条件画出可行域,如图所示,其中 .由 得 ,当直线
过 时,在 轴上的截距最大,所以 有最大值为 .故选C.
77.(2019·天津·文·)设变量 满足约束条件 则目标函数 的最大值为 ( )
A.2 B.3 C.5 D.6
【答案】【答案】C
【解析】由约束条件 作出可行域如图
联立 ,解得 ,化目标函数 为 ,由图可知,当直线
过 时, 有最大值为5.故选C.
二填空题
1.(2023年全国乙卷文科·)若x,y满足约束条件 ,则 的最大值为______.
2.【答案】8
【解析】:作出可行域如下图所示:
,移项得 ,联立有 ,解得 ,
设 ,显然平移直线 使其经过点 ,此时截距 最小,则 最大,
代入得 ,故答案为:8.
82.(2023年全国甲卷文科·)若x,y满足约束条件 ,设 的最大值为____________.
【答案】15
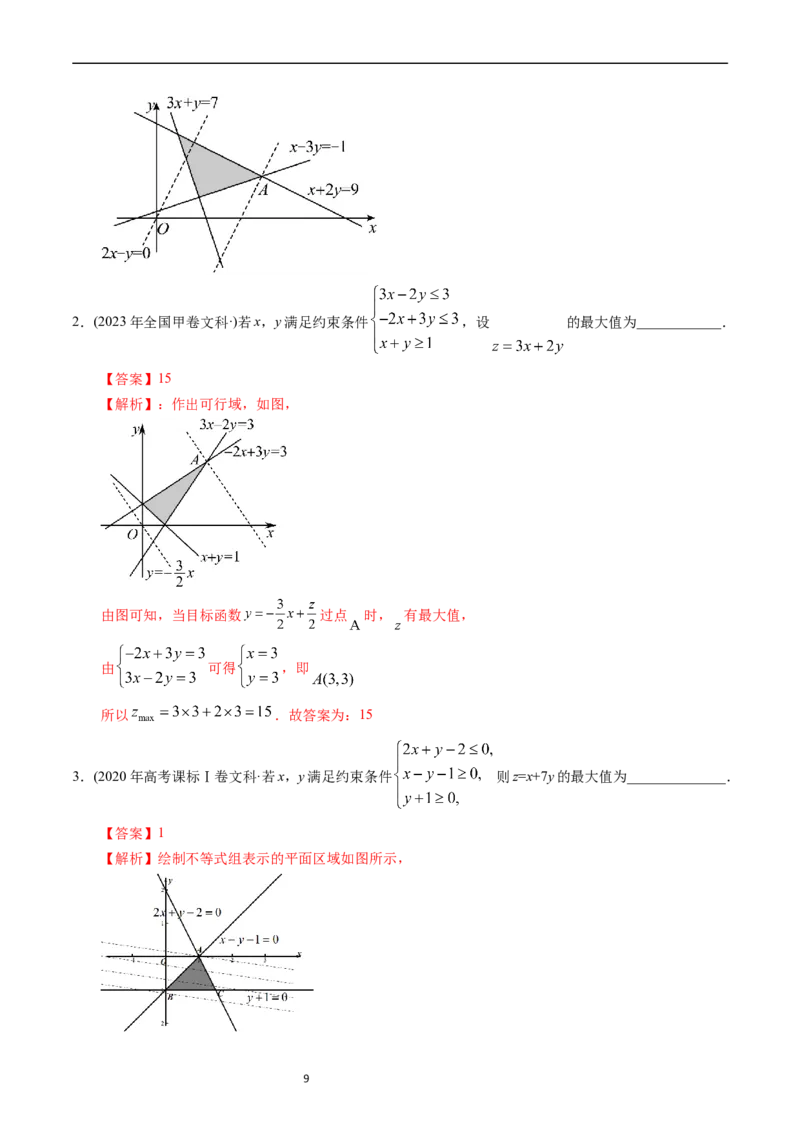
【解析】:作出可行域,如图,
由图可知,当目标函数 过点 时, 有最大值,
由 可得 ,即 ,
所以 .故答案为:15
3.(2020年高考课标Ⅰ卷文科·若x,y满足约束条件 则z=x+7y的最大值为______________.
【答案】1
【解析】绘制不等式组表示的平面区域如图所示,
9目标函数 即: ,
其中z取得最大值时,其几何意义表示直线系在y轴上的截距最大,
据此结合目标函数的几何意义可知目标函数在点A处取得最大值,
联立直线方程: ,可得点A的坐标为: ,
据此可知目标函数的最大值为: .故答案 为:1.
4.(2020年高考课标Ⅱ卷文科·)若x,y满足约束条件 则 的最大值是__________.
【答案】
【解析】不等式组表示的平面区域为下图所示:
平移直线 ,当直线经过点 时,直线 在纵轴上的截距最大,
此时点 的坐标是方程组 的解,解得: ,
因此 的最大值为: .故答案为: .
5.(2020年高考课标Ⅲ卷文科·第13题)若x,y满足约束条件 ,则z=3x+2y的最大值为
_________.
【答案】7
【解析】不等式组所表示的可行域如图
因为 ,所以 ,易知截距 越大,则 越大,
10平移直线 ,当 经过A点时截距最大,此时z最大,
由 ,得 , ,所以 .故答案为:7.
6.(2019·上海·文理)已知 满足 ,求 的最小值为________.
【答案】
【解析】线性规划作图:后求出边界点代入求最值,当 , 时, .
7.(2019·全国Ⅱ·文·)若变量 满足约束条件 则 的最大值是
___________.
【答案】9
【解析】画出不等式组表示的可行域,如图所示,
阴影部分表示的三角形 区域,根据直线 中的 表示纵截距的相反数,当直线
过点 时, 取最大值为9.
考点04 不等式综合应用
11一 单选题
1.(2023年全国乙卷文科·)已知实数 满足 ,则 的最大值是 ( )
A. B.4 C. D.7
【答案】C【解析】:法一:令 ,则 ,
代 入 原 式 化 简 得 , 因 为 存 在 实 数 , 则 , 即
,化简得 ,解得 ,
故 的最大值是 ,
法二: ,整理得 ,
令 , ,其中 ,
则 ,
,所以 ,则 ,即 时, 取得最大值 ,
法三:由 可得 ,设 ,则圆心到直线
的距离 ,解得 故选:C.
2 . (2019· 天 津 · 理 ) 已 知 , , , 则 的 大 小 关 系 为
( )
A. B. C. D.
【答案】A
【解析】: , ,即
,
,所以 .
3.(2020年浙江省高考数学试卷)已知a,b R且ab≠0,若(x–a)(x–b)(x–2a–b)≥0在x≥0上恒成立,
则 ( )
A.a<0 B.a>0 C.b<0 D.b>0
【答案】C
12【解析】:因为 ,所以 且 ,设 ,则 零的点
为
当 时,则 , ,要使 ,必有 ,且 ,
即 ,且 ,所以 ;
当 时,则 , ,要使 ,必有 .综上一定有 . 故选:C
4.(2020年浙江省高考数学试卷·)已知a,b R且ab≠0,若(x–a)(x–b)(x–2a–b)≥0在x≥0上恒成立,则 (
)
A.a<0 B.a>0 C.b<0 D.b>0
【答案】C
【解析】:因为 ,所以 且 ,设 ,则 的零点
为 当 时,则 , ,要使 ,必有 ,且 ,
即 ,且 ,所以 ;当 时,则 , ,要使 ,必有 .综上
一定有 . 故选:C
5.(2019·全国Ⅰ·理) 已知 , , ,则 ( )
A. B. C. D.
【答案】答案:B
【解析】: , , ,故 .
二、填空题
1.(2022年高考全国甲卷数学(理))已知 中,点D在边BC上, .当
取得最小值时, ________.
2.(2021年高考浙江卷)我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三
角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别是3,4,
记大正方形的面积为 ,小正方形的面积为 ,则 ___________.
1314