2024届质检（一）物理参考答案_2024年3月_013月合集_2024届河北省石家庄市普通高中学校毕业年级教学质量检测(一)_2024届河北省石家庄市普通高中学校毕业年级教学质量检测(一)物理

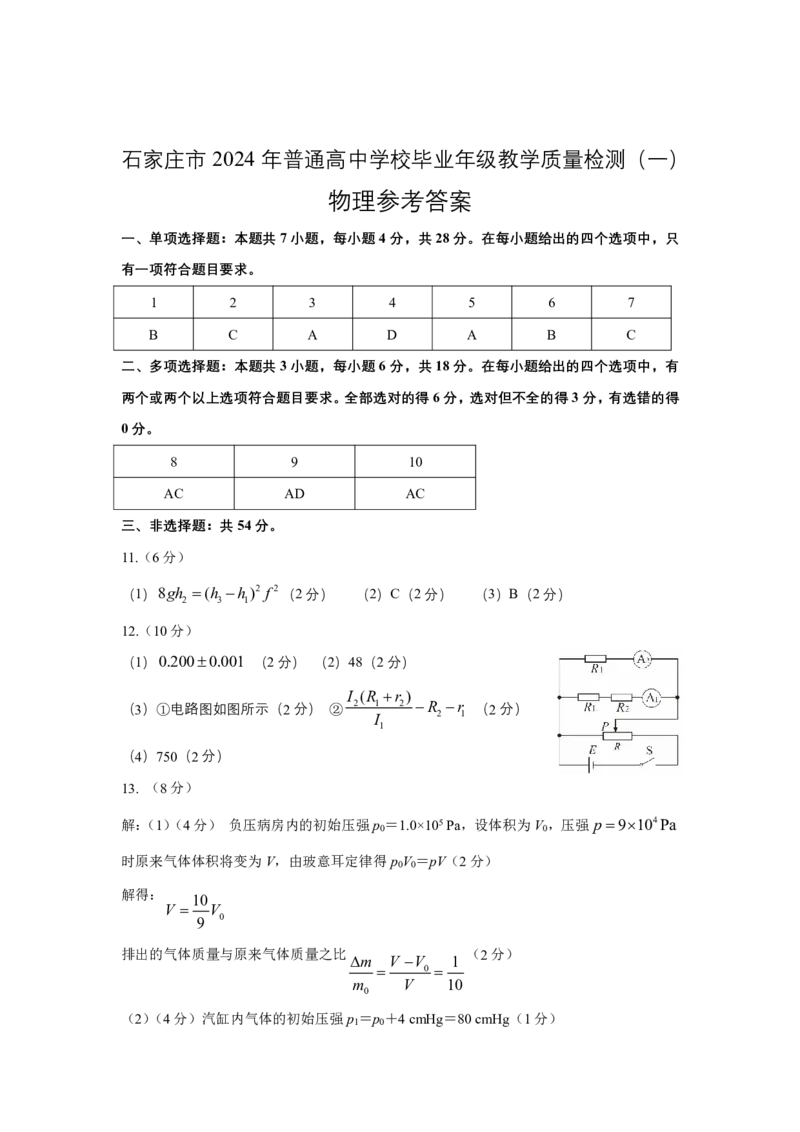
石家庄市 2024 年普通高中学校毕业年级教学质量检测（一） 物理参考答案 一、单项选择题：本题共7小题，每小题4分，共28分。在每小题给出的四个选项中，只 有一项符合题目要求。 1 2 3 4 5 6 7 B C A D A B C 二、多项选择题：本题共3小题，每小题6分，共18分。在每小题给出的四个选项中，有 两个或两个以上选项符合题目要求。全部选对的得6分，选对但不全的得3分，有选错的得 0分。 8 9 10 AC AD AC 三、非选择题：共54分。 11.（6分） （1）8gh (h h)2 f 2（2分） （2）C（2分） （3）B（2分） 2 3 1 12.（10分） （1）0.2000.001 （2分） （2）48（2分） I (R r ) （3）①电路图如图所示（2分） ② 2 1 2 R r （2分） I 2 1 1 （4）750（2分） 13. （8分） 解：（1）（4分） 负压病房内的初始压强p ＝1.0×105Pa，设体积为V ，压强 p9104Pa 0 0 时原来气体体积将变为V，由玻意耳定律得p V ＝pV（2分） 0 0 解得： 10 V  V 9 0 排出的气体质量与原来气体质量之比 （2分） m V V 1  0  m V 10 0 （2）（4分）汽缸内气体的初始压强p ＝p ＋4cmHg＝80cmHg（1分） 1 0 {#{QQABQYIQggCIAAIAAAhCQwUKCAOQkBGCCAoGBFAAIAABiBFABAA=}#}加热后两侧液面高度差为12cm p ＝p ＋12cmHg＝88cmHg（1分） 2 0 p p 由查理定律得 1  2 （1分） T T 1 2 解得T ＝330K（1分） 2 14. （14分） 解：设水平向右为正方向。 （1）（3分）由图像可知，图线与时间轴围成的图形面积为力F在0-2s内的冲量， I mgt mv 对物块A在0-4s内，由动量定理可得： F 1 1（2分） 解得： m/s（1分） （2）（ 6 1 =分）12AB发生弹性碰撞，系统动量守恒和能量守恒 mv mvm v 1 1 1 1 2 2 （1分） 1 1 1 mv2  mv2 m v 2 （1分） 2 1 1 2 1 1 2 2 2 解得： m/s，v 12m/s 2 ' 由于小车v1 足=够0长，离墙壁足够远，故小车与墙壁碰撞前已和滑块B共速，由动量守恒可得 （1分） ' m解2得v2：= m2+mm/s 0 v2 ' 小车与墙v2壁=完8成第1次碰撞后，车速变为 m/s 小车与墙壁第2次碰撞前与滑块B再次共v速3，=−由4动量守恒可得 （1分） ' ' m解2得v2：+m0v3 m=/sm2+m0 v3 ' 由系统功v3能=关4系可得，小车与墙壁第1次碰撞后到与墙壁第2次碰撞前瞬间的过程中滑块与 小车间由于摩擦产生的热量 （1分） 1 '2 1 2 1 '2 Q解=得2：m2v2+2（m 1 0v分 3 ）−2 m2+m0 v3 （3）（Q5分=）48由J 小车与墙壁第1次碰后和第2次碰前小车与滑块共速时的速度大小可推断， 从第1次碰撞结束，每次小车与滑块共速后立即与墙壁发生碰撞。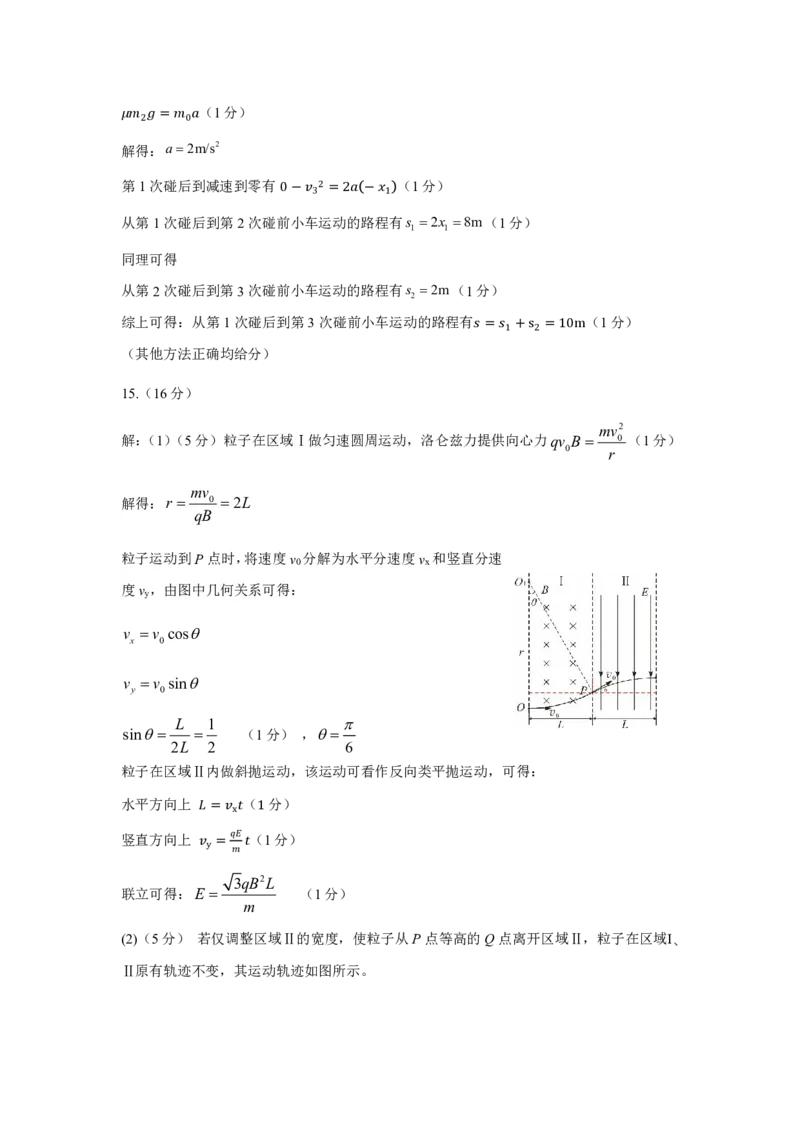以小车为研究对象，由牛 顿第二定律可得 {#{QQABQYIQggCIAAIAAAhCQwUKCAOQkBGCCAoGBFAAIAABiBFABAA=}#}（1分） 解 得 2 ： = a  0 2 m/s2 第1次碰后到减速到零有 （1分） 2 从第1次碰后到第2次碰前 0 小 − 车 3 运 = 动 2 的 路 − 程 1 有s 2x 8m（1分） 1 1 同理可得 从第2次碰后到第3次碰前小车运动的路程有s 2m（1分） 2 综上可得：从第1次碰后到第3次碰前小车运动的路程有 （1分） （其他方法正确均给分） = 1+s2 =10m 15.（16分） mv2 解：（1）（5分）粒子在区域Ⅰ做匀速圆周运动，洛仑兹力提供向心力qv B  0 （1分） 0 r mv 解得：r  0 2L qB 粒子运动到P点时，将速度v 分解为水平分速度v 和竖直分速 0 x 度v ，由图中几何关系可得： y v v cos x 0 v v sin y 0 L 1  sin  （1分） ， 2L 2 6 粒子在区域Ⅱ内做斜抛运动，该运动可看作反向类平抛运动，可得： 水平方向上 （ 分） 竖直方向上 = x （1 1分） y = 3qB2L 联立可得：E  （1分） m (2)（5分） 若仅调整区域Ⅱ的宽度，使粒子从P点等高的Q点离开区域Ⅱ，粒子在区域Ⅰ、 Ⅱ原有轨迹不变，其运动轨迹如图所示。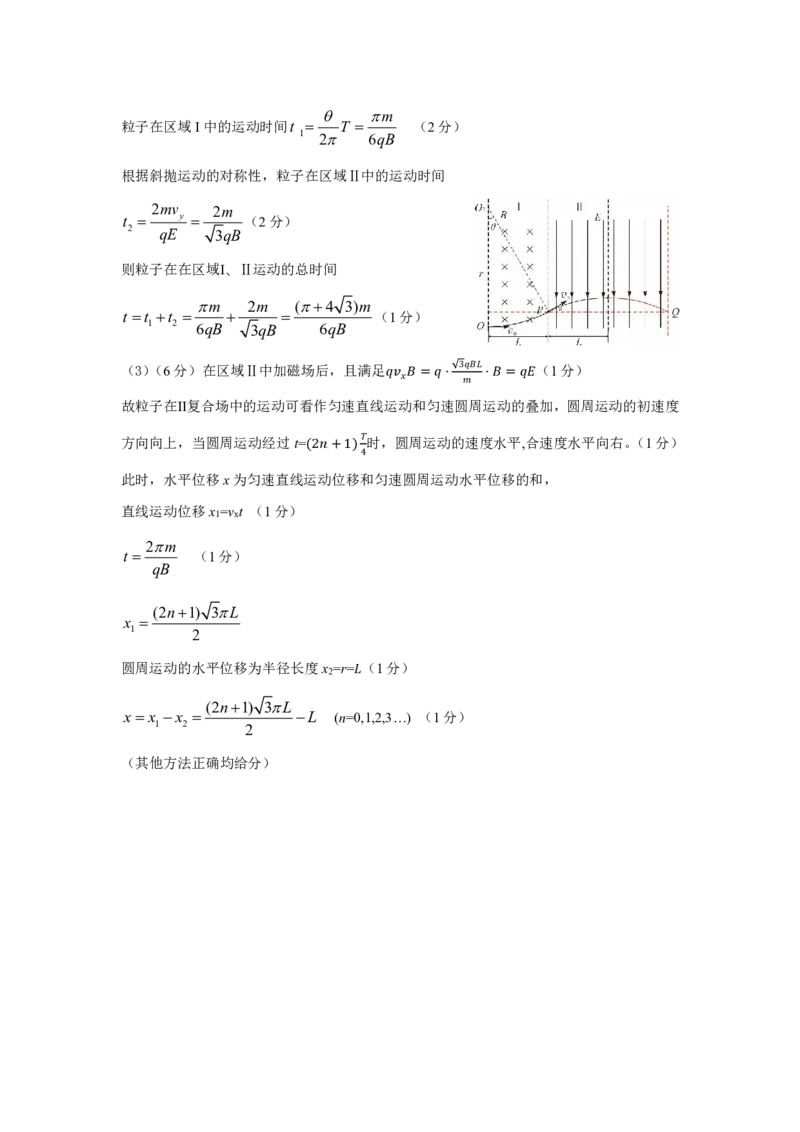 {#{QQABQYIQggCIAAIAAAhCQwUKCAOQkBGCCAoGBFAAIAABiBFABAA=}#} m 粒子在区域I中的运动时间t  T  （2分） 1 2 6qB 根据斜抛运动的对称性，粒子在区域Ⅱ中的运动时间 2mv 2m t  y  （2分） 2 qE 3qB 则粒子在在区域Ⅰ、Ⅱ运动的总时间 m 2m (4 3)m t t t    （1分） 1 2 6qB 3qB 6qB （3）（6分）在区域Ⅱ中加磁场后，且满足 （1分） 3 故粒子在Ⅱ复合场中的运动可看作匀速直线运 动 和=匀 速⋅ 圆 周运⋅ 动=的 叠 加，圆周运动的初速度 方向向上，当圆周运动经过t= 时，圆周运动的速度水平,合速度水平向右。（1分） 此时，水平位移x为匀速直线运 (2 动 + 位 1 移 ) 和4 匀速圆周运动水平位移的和， 直线运动位移x =v t （1分） 1 x 2m t  （1分） qB (2n1) 3L x  1 2 圆周运动的水平位移为半径长度x =r= （1分） 2 (2n1) 3L x x x  L (n=0,1,2,3…) （1分） 1 2 2 （其他方法正确均给分） {#{QQABQYIQggCIAAIAAAhCQwUKCAOQkBGCCAoGBFAAIAABiBFABAA=}#}