2024年2月浙江省杭州二中高三年级开学考数学-试题卷(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套

绝密★启用前 2023 学年第二学期浙江省杭州二中 2 月开学考 高三数学试题卷 考生须知： 1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并认真核准准考证号条 形码上的以上信息，将条形码粘贴在答题卡上的指定位置。 2．请按题号顺序在答题卡上各题目的答题区域内作答，写在试卷、草稿纸和答题卡上的 非答题区域均无效。 3．选择题用 2B铅笔在答题卡上把所选答案的标号涂黑；非选择题用黑色签字笔在答题卡 上作答；字体工整，笔迹清楚。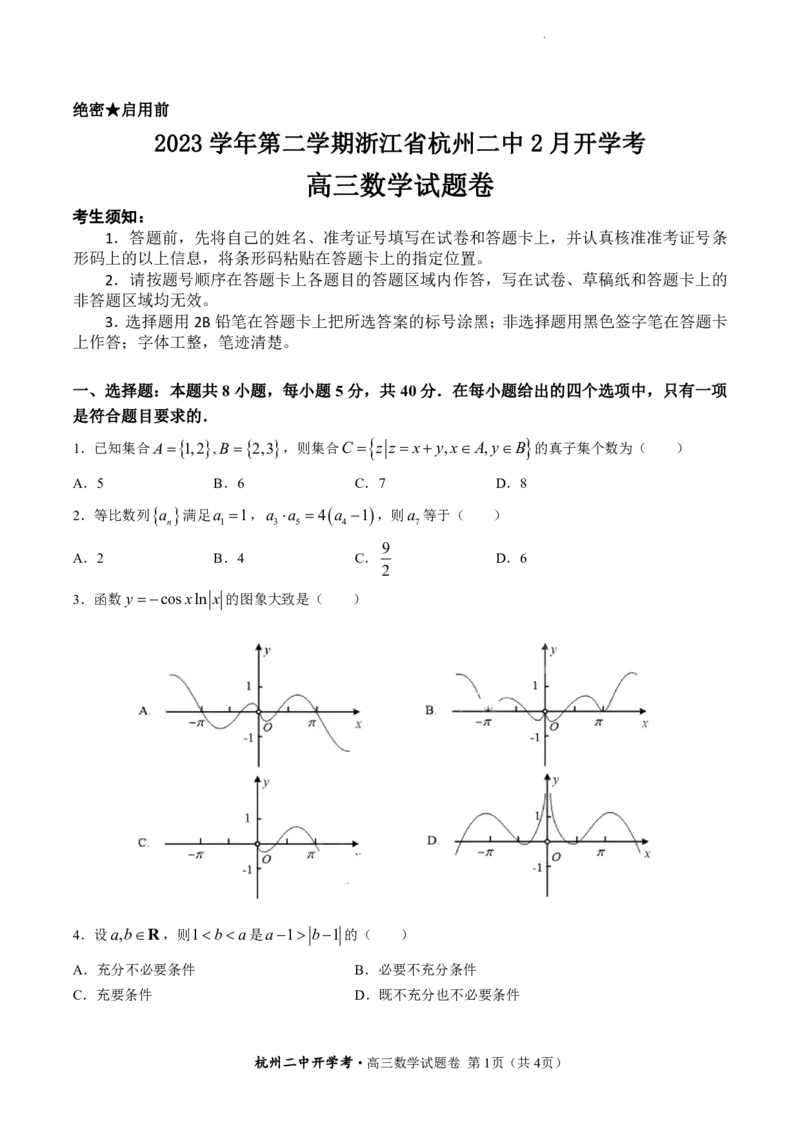 一、选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有一项 是符合题目要求的． 1．已知集合A 1,2  ,B  2,3 ，则集合C   z z  x y,xA,yB  的真子集个数为（ ） A．5 B．6 C．7 D．8 2．等比数列 a 满足a 1，a a 4  a 1 ，则a 等于（ ） n 1 3 5 4 7 9 A．2 B．4 C． D．6 2 3．函数y cosxln x 的图象大致是（ ） 4．设a,bR，则1ba是a1 b1的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 杭州二中开学考·高三数学试题卷 第1页（共4页） {#{QQABAYIEggCIABAA学科A网（北京A）股份g有CQwVICAAQkBEAAIoORAAIIAIBSQNABAA=}#}π 5．已知a 0.75，b2log 2，csin ，则a,b,c的大小关系是（ ） 5 5 A．cba B．bca C．acb D．c 6  2 x4 6．在x1  的展开式中， 的系数为（ ）  y y2 A．60 B．60 C．120 D．120 x2 y2 π 7．椭圆C:  1  a b 0 的左、右焦点分别为F ，F ，P为椭圆上一点，且FPF  ，若F a2 b2 1 2 1 2 3 1 关于FPF 平分线的对称点在椭圆C上，则该椭圆的离心率为（ ） 1 2 2 3 1 1 A． B． C． D． 2 3 2 3  π  5π 3  π 8．若sin  cos    ，则cos2  （ ）  4  12 4  6 3 3 1 3 1 3 A．1 B．1 C．  D．  2 2 2 2 2 2 二、选择题：本题共 3小题，每小题 6分，共 18分，在每小题给出的选项中，有多项符合题 目要求，全部选对的得 6分，部分选对的得部分分，有选错的得 0分． 9．设，，为互不重合的平面，m，n为互不重合的直线，则下列命题为真命题的是（ ） A．若∥，∥，则∥ B．若m，m，则， C．若m∥，n∥，m∥n，则∥ D．若，，则∥ 10．有一组互不相等的样本数据x ,x ,,x ，平均数为x．若随机剔除其中一个数据，得到一组新数据， 1 2 6 记为 y ,y ,,y ，平均数为y，则（ ） 1 2 5 A．新数据的极差可能等于原数据的极差 B．新数据的中位数不可能等于原数据的中位数 C．若x  y，则新数据的方差一定大于原数据方差 D．若x  y，则新数据的40%分位数一定大于原数据的40%分位数 11．记函数 f  x 2cos x0,0 π 的最小正周期为T，若 f  T  3，且 f  x 在  π π   ,  上的最大值与最小值的差为3，则（ ）  3 3 杭州二中开学考·高三数学试题卷 第2页（共4页） {#{QQABAYIEggCIABAA学科A网（北京A）股份g有CQwVICAAQkBEAAIoORAAIIAIBSQNABAA=}#} π π A． f  0 1 B． f     f    3 9  π 2π 3 C． f  x 在区间   ,  上单调递减 D．直线y 3 x是曲线 y  f  x 的切线  9 3  2 三、填空题：本题共 3小题，每小题 5分，共 15分． ex, x1 12．设函数 f  x  ，则 f  1 ______；若 f  a 1，则实数a ______． lnx, x1 13．设z ，z 是复数，已知 z 1， z 3， z z  5，则 z z ______． 1 2 1 2 1 2 1 2 BDBE 1 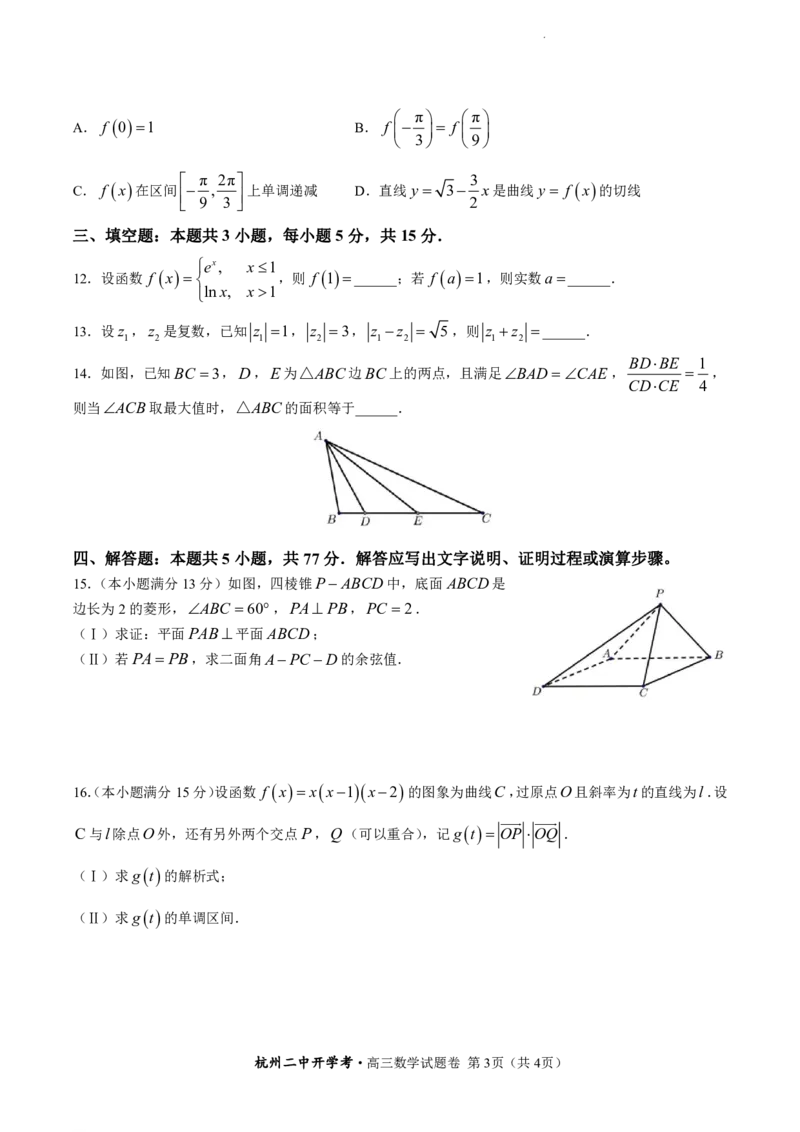14．如图，已知BC 3，D，E为△ABC边BC上的两点，且满足BAD CAE，  ， CDCE 4 则当ACB取最大值时，△ABC的面积等于______． 四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤。 15．（本小题满分13分）如图，四棱锥P ABCD中，底面ABCD是 边长为2的菱形，ABC 60，PAPB，PC 2． （Ⅰ）求证：平面PAB平面ABCD； （Ⅱ）若PA PB，求二面角APCD的余弦值． 16．（本小题满分15分）设函数 f  x  x  x1  x2 的图象为曲线C，过原点O且斜率为t的直线为l．设   C与l除点O外，还有另外两个交点P，Q（可以重合），记g  t  OP OQ ． （Ⅰ）求g  t 的解析式； （Ⅱ）求g  t 的单调区间． 杭州二中开学考·高三数学试题卷 第3页（共4页） {#{QQABAYIEggCIABAA学科A网（北京A）股份g有CQwVICAAQkBEAAIoORAAIIAIBSQNABAA=}#}17．（本小题满分15分）“英才计划”最早开始于2013年，由中国科协、教育部共同组织实施，到2023年 已经培养了6000多名具有创新潜质的优秀中学生，为选拔培养对象，某高校在暑假期间从中学里挑选优秀 学生参加数学、物理、化学学科夏令营活动． （Ⅰ）若数学组的7名学员中恰有3人来自A中学，从这7名学员中选取3人，表示选取的人中来自A中 学的人数，求的分布列和数学期望； （Ⅱ）在夏令营开幕式的晚会上，物理组举行了一次学科知识竞答活动，规则如下：两人一组，每一轮竞 答中，每人分别答两题，若小组答对题数不小于3，则取得本轮胜利．已知甲乙两位同学组成一组，甲、乙 4 答对每道题的概率分别为 p ， p ．假设甲、乙两人每次答题相互独立，且互不影响．当 p  p  时， 1 2 1 2 3 求甲、乙两位同学在每轮答题中取胜的概率的最大值． 18．（本小题满分17分）已知抛物线C :x2 4y的焦点为F ．设M  x ,y （其中x 0， y 0）为 1 0 0 0 0 拋物线C :x2 4  y1 上一点．过M 作抛物线C 的两条切线MA，MB，A，B为切点．射线MF交 2 1 抛物线C 于另一点D． 2 （Ⅰ）若x 2，求直线AB的方程； 0 （Ⅱ）求四边形MADB面积的最小值．   19．（本小题满分17分）设整数n,k 满足1k n，集合A 2m 0mn1,mZ ．从A中选取k 个 不同的元素并取它们的乘积，这样的乘积有Ck个，设它们的和为a ．例如 n n,k a 20212022 2122 14． 3,2 （Ⅰ）若n2，求a ； n,2     f x f x （Ⅱ）记 f  x 1a xa x2 a xn．求 n1 和 n1 的整式表达式； n n,1 n,2 n,n f  x  f  2x  n n a （Ⅲ）用含n，k 的式子来表示 n1,k1 ． a n,k 杭州二中开学考·高三数学试题卷 第4页（共4页） {#{QQABAYIEggCIABAA学科A网（北京A）股份g有CQwVICAAQkBEAAIoORAAIIAIBSQNABAA=}#}