2024年3月长望浏宁高三调研考试数学参考答案_2024年3月_013月合集_2024届湖南省长沙市四区市高三下学期3月调研考试（一模）

绝密★启用前 2024 年 3 月高三调研考试试卷 数学 参考答案与试题解析 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目 要求的. 题号 1 2 3 4 5 6 7 8 答案 B C A B A C D D 1．集合A＝{x|﹣1≤x≤2}，B＝{x|x＜1}，则 高三数学参考答案 第1页（共11页） 学科网（北京）股份有限公司 A   R B  ＝（ ） A．{x|x＞1} B．{x|x≥﹣1} C．{x|1＜x≤2} D．{x|1≤x≤2} 【解答】：由A＝{x|﹣1≤x≤2}，B＝{x|x＜1}，所以∁R B＝{x|x≥1}，所以A∪（∁R B）＝{x|x≥﹣1}． 故选：B． 2．已知 S n 为等差数列  a n  的前n项和，若 ， a 6 3 ， 则 S 8 （ ） A．76 B．72 C．36 D．32 【解答】： S 8 8 ( a 1 2 a 8 ) 8 ( a 3 2 a 6 ) 3 6 . 故选C. 3．设α，β是两个不同的平面，a，b是两条不同的直线，且a⊥α，b⊂β，则“a∥b”是“α⊥β”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【解答】：由a⊥α，a∥b，则b⊥α，又b⊂β，所以α⊥β，故“a∥b”是“α⊥β”的充分条件． 当满足α⊥β，a⊥α，b⊂β时，直线a，b可能平行，可能相交，也可能异面． 故“a∥b”不是“α⊥β”的必要条件．故选：A． 4.已知双曲线 C x2 y2 ：  1b0的一个焦点到一条渐近线的距离为2，则双曲线 4 b2 C 的离心率为（ ） 3 3 5 A． B． 2 C． D． 2 2 3 【解答】：双曲线C： x 4 2  y b 2 2  1  a  0 , b  0  的一个焦点到一条渐近线的距离为2，b2， 因此双 2 c b 曲线C的离心率e  1  2.故选：B. 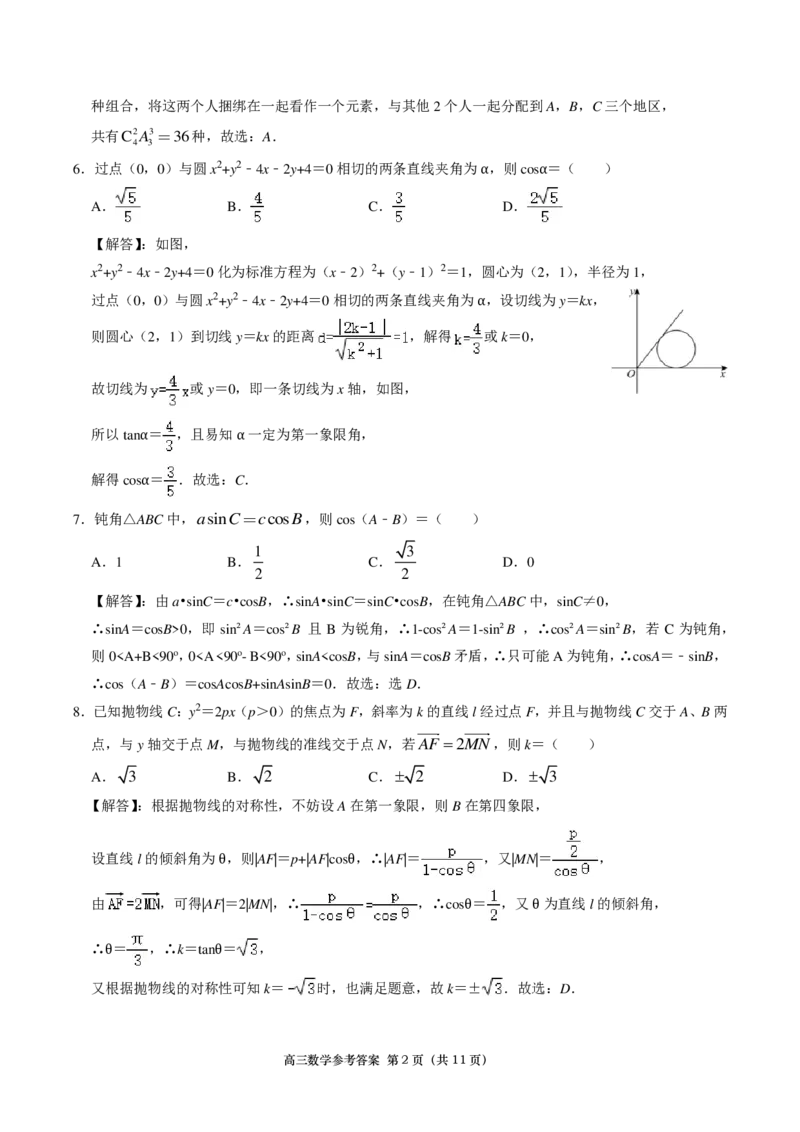  a a 5．将甲、乙、丙、丁4个人全部分配到A，B，C三个地区工作，每个地区至少有1人，则不同的分配方案 为（ ） A．36种 B．24种 C．18种 D．16种 【解答】：由题意，A，B，C三个地区中必有一个地区有2人，先在甲、乙、丙、丁4个人中选2个人有C2 4 a 3 6 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}种组合，将这两个人捆绑在一起看作一个元素，与其他2个人一起分配到A，B，C三个地区， 共有C2A3 36种，故选：A． 4 3 6．过点（0，0）与圆x2+y2﹣4x﹣2y+4＝0相切的两条直线夹角为α，则cosα＝（ ） A． B． C． D． 【解答】：如图， x2+y2﹣4x﹣2y+4＝0化为标准方程为（x﹣2）2+（y﹣1）2＝1，圆心为（2，1），半径为1， 过点（0，0）与圆x2+y2﹣4x﹣2y+4＝0相切的两条直线夹角为α，设切线为y＝kx， 则圆心（2，1）到切线y＝kx的距离 ，解得 或k＝0， 故切线为 或y＝0，即一条切线为x轴，如图， 所以tanα＝ ，且易知α一定为第一象限角， 解得cosα＝ ．故选：C． 7．钝角△ABC中，asinC ccosB，则cos（A﹣B）＝（ ） A．1 B． 高三数学参考答案 第2页（共11页） 学科网（北京）股份有限公司 1 2 C． 2 3 D．0 【解答】：由a•sinC＝c•cosB，∴sinA•sinC＝sinC•cosB，在钝角△ABC中，sinC≠0， ∴sinA＝cosB>0，即 sin²A＝cos²B 且 B 为锐角，∴1-cos²A＝1-sin²B ，∴cos²A＝sin²B，若 C 为钝角， 则0