2024年3月高三调研考试试卷_2024年3月_013月合集_2024届湖南省长沙市四区市高三下学期3月调研考试（一模）

2024 年 3 月高三调研考试 科目：数 学 （试题卷） 注意事项： 1．本试题卷共 5 页，共四个大题，19 个小题。总分 150 分，考试时量 120 分钟。 2．接到试卷后，请检查是否有缺页、缺题或字迹不 清等问题。如有，请及时报告监考老师。 3．答题前，务必将自己的姓名、考号写在答题卡和 该试题卷的封面上，并认真核对条形码的姓名、考号和科 目。 4．作答时，请将答案写在答题卡上。在草稿纸、试 题卷上答题无效。 姓 名 准考证号 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}绝密★启用前 2024 年 3 月高三调研考试试卷 数 学 (长沙县、望城区、浏阳市、宁乡市联合命制) 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有 一项是符合题目要求的. 1．集合A＝{x|1≤x≤2}，B＝{x|x＜1}，则AC B＝（ ） R A．{x|x＞1} B．{x|x≥1} C．{x|1＜x≤2} D．{x|1≤x≤2} 2．已知S 为等差数列 a  的前n项和，若a = 6 ，a = 3，则 S =（ ） n n 3 6 8 A．76 B．72 C．36 D．32 3．设，是两个不同的平面，a，b是两条不同的直线，且a⊥，b⊂，则“a∥ b”是“⊥”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 x2 y2 4.已知双曲线C：  1  b0  的一个焦点到一条渐近线的距离为2，则双曲线C的 4 b2 离心率为（ ） 3 3 5 A． B． 2 C． D． 3 2 2 5．将甲、乙、丙、丁4个人全部分配到A，B，C三个地区工作，每个地区至少有1人， 则不同的分配方案为（ ） A．36种 B．24种 C．18种 D．16种 第 1 页 共 5 页 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}6．过点（0，0）与圆x2+ y2﹣4x﹣2 y+4＝0相切的两条直线夹角为，则cos＝（ ） 5 4 3 2 5 A． B． C． D． 5 5 5 5 7．钝角△ABC中，asinC= ccosB，则cos(A﹣B)＝（ ） 1 3 A．1 B． C． D．0 2 2 8.已知抛物线C：y2＝2px（p＞0）的焦点为F，斜率为k的直线l经过点F，并且与抛物   线C交于A、B两点，与y轴交于点M，与抛物线的准线交于点N，若AF 2MN， 则k＝（ ） A． 3 B． 2 C． 2 D． 3 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符 合题目要求。全部选对的得6分，部分选对的得2分，有选错的得0分。 9．设z为非零复数，则下列命题中正确的是（ ） A．z2＝|z|2 B． z 2  zz C． z2 = z2 D．若|z|＝1，则|z+i|的最大值为2 1   10.已知函数 f(x) cos(2x )，把y＝f（x）的图象向右平移 个单位长度，得到 2 3 3 函数y＝g（x）的图象，以下说法正确的是（ ）  A．x 是y＝f（x）图象的一条对称轴 6   2 B．f（x）的单调递减区间为 k ,k   kZ   6 3  C．y＝g（x）的图象关于原点对称 1 D．f（x）+g（x）的最大值为 2 第 2 页 共 5 页 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}11．已知f（x）是定义在R上的连续函数，且满足f（x+y）＝f（x）+f（y）﹣2xy， 当x＞0时，f（x）＞0，设g（x）＝f（x）+x2（ ） A．若f（1）•f（﹣1）＝﹣3，则f（1）＝1 B．g（x）是偶函数 C．g（x）在R上是增函数 D． ( x- 1 ) g(x)> 0的解集是（﹣∞，0）∪（1，+∞） 三、填空题：本题共3小题，每小题5分，共15分。 12．已知一组数据如下：4，4，4，7，7，8，8，9，9，10，则这组数据的第75百分 位数是 ． 13．一个正四棱锥底面边长为 2，高为 3 ，则该四棱锥的内切球表面积 为 ． a ( ln x - ln x ) 1 14．已知对任意x 1 ，x 2   0，  ，且当x 1  x 2 时，都有： x 2 - x 1 < 1+ x x ， 2 1 1 2 则a的取值范围是 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。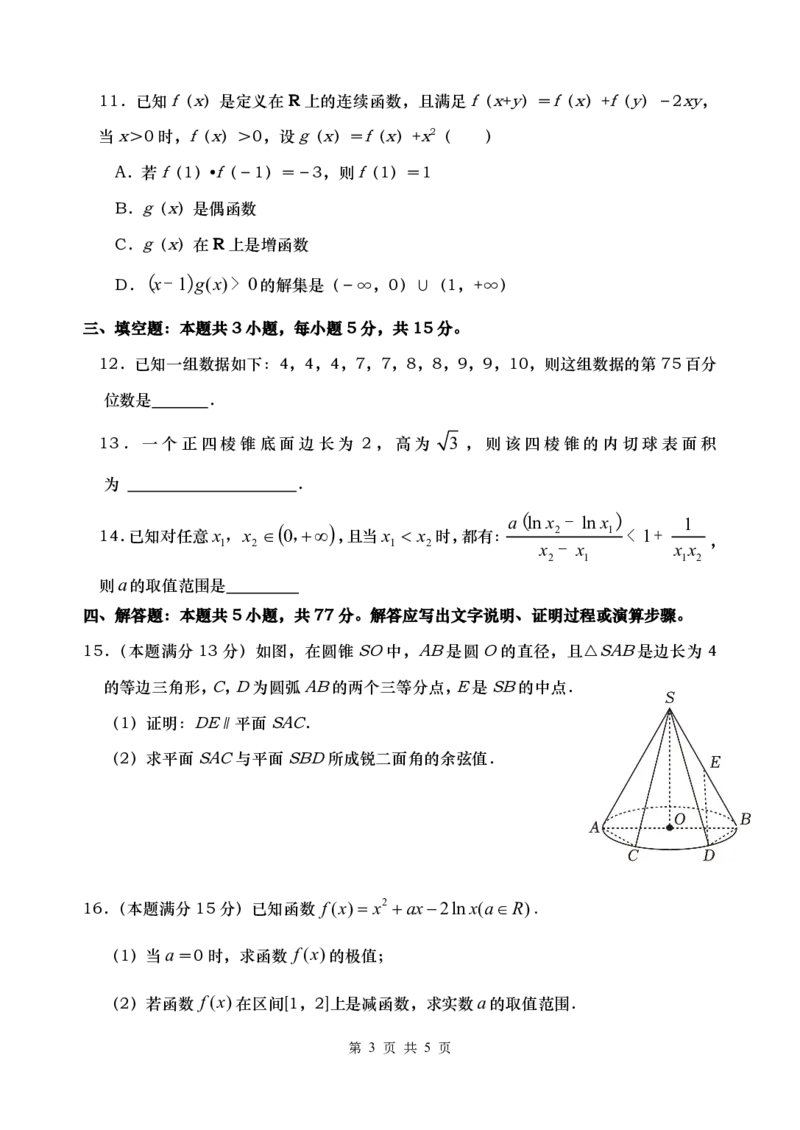 15．（本题满分13分）如图，在圆锥SO中，AB是圆O的直径，且△SAB是边长为4 的等边三角形，C，D为圆弧AB的两个三等分点，E是SB的中点． （1）证明：DE∥平面SAC． （2）求平面SAC与平面SBD所成锐二面角的余弦值． 16．（本题满分15分）已知函数 f(x) x2 ax2lnx(aR). （1）当a＝0时，求函数 f(x)的极值； （2）若函数 f(x)在区间[1，2]上是减函数，求实数a的取值范围． 第 3 页 共 5 页 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}17．（本题满分15分）春节临近，为了吸引顾客，我市某大型商超策划了抽奖活动，计划 如下：有A、B、C三个抽奖项目，它们之间相互不影响，每个项目每位顾客至多参加 1 2 一次，项目A中奖的概率是 ，项目B和C中奖的概率都是 ． 4 5 （1）若规定每位参加活动的顾客需要依次参加A、B、C三个项目，如果A、B、C 三个项目全部中奖，顾客将获得100元奖券；如果仅有两个项目中奖，他将获得50元 奖券；否则就没有奖券，求每位顾客获得奖券金额的期望； （2）若规定每位顾客等可能地参加三个项目中的一个项目．已知某顾客中奖了，求 他参加的是A项目的概率． 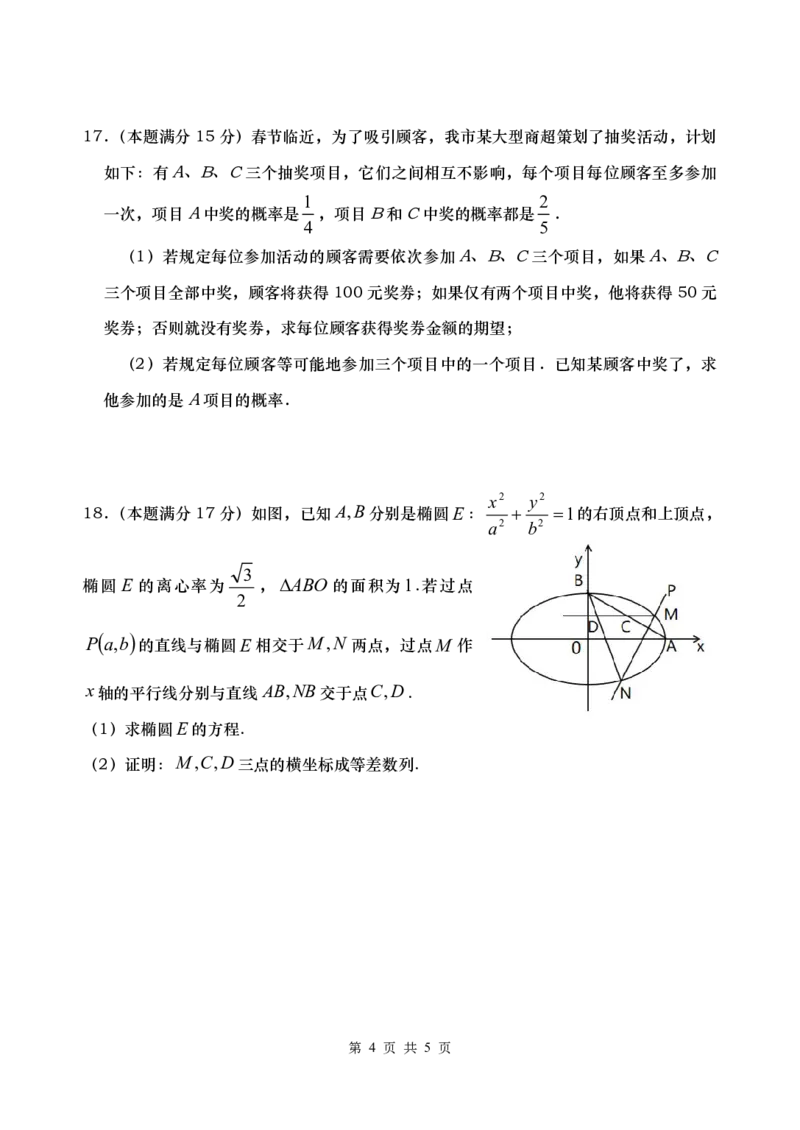x2 y2 18．（本题满分17分）如图，已知A,B分别是椭圆E：  1的右顶点和上顶点， a2 b2 3 椭圆 E 的离心率为 ，ABO 的面积为1.若过点 2   P a,b 的直线与椭圆E相交于M,N 两点，过点M 作 x轴的平行线分别与直线AB,NB交于点C,D. （1）求椭圆E的方程. （2）证明：M,C,D三点的横坐标成等差数列. 第 4 页 共 5 页 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}19.（本题满分17分）若存在常数t，使得数列{a }满足a aa a a t （n≥1，n n n1 1 2 3 n   ∈N），则称数列 a 为“H（t）数列”． n （1）判断数列：1，2，3，8，49是否为“H（1）数列”，并说明理由；         （2）若数列 a 是首项为2的“H（t）数列”，数列 b 是等比数列，且 a 与 b n n n n n 满足 a2 aa a a log b ，求t的值和数列  b  的通项公式； i 1 2 3 n 2 n n i1 （3）若数列  a  是“H（t）数列”，S 为数列  a  的前n项和，a 1，t＞0，试比 n n n 1 较lna 与a 1的大小，并证明 t  S S eS n n. n n n1 n 第 5 页 共 5 页 {#{QQABbYgEogCAABIAAQhCEwHKCAGQkAECCIoOQEAMMAAACBFABCA=}#}