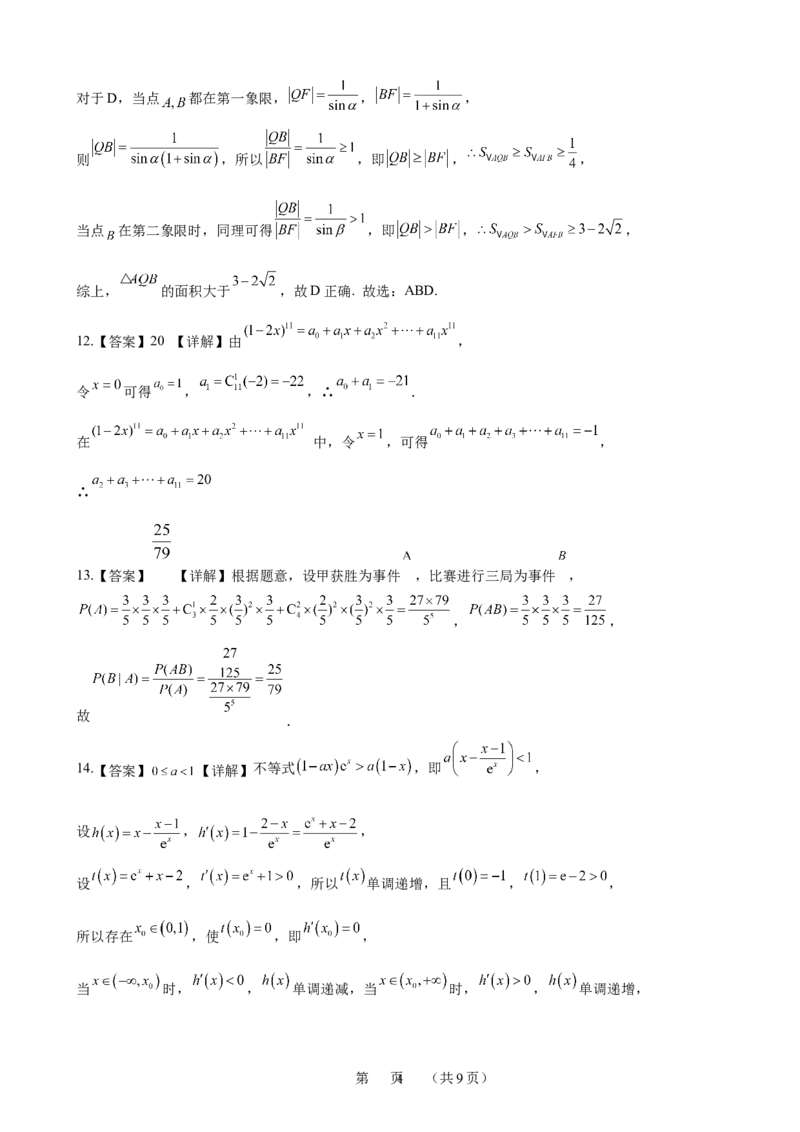文档内容
202 4年广州市普通高中毕业班冲刺训练题(三)参考答案
1. 答案:D【详解】因为 , ,所以
2、答案:B【详解】因为复数 ,所以 对应的点为 ,位于第二象限.
3.答案:B【详解】因为 为等差数列, ,所以 ,所以
.
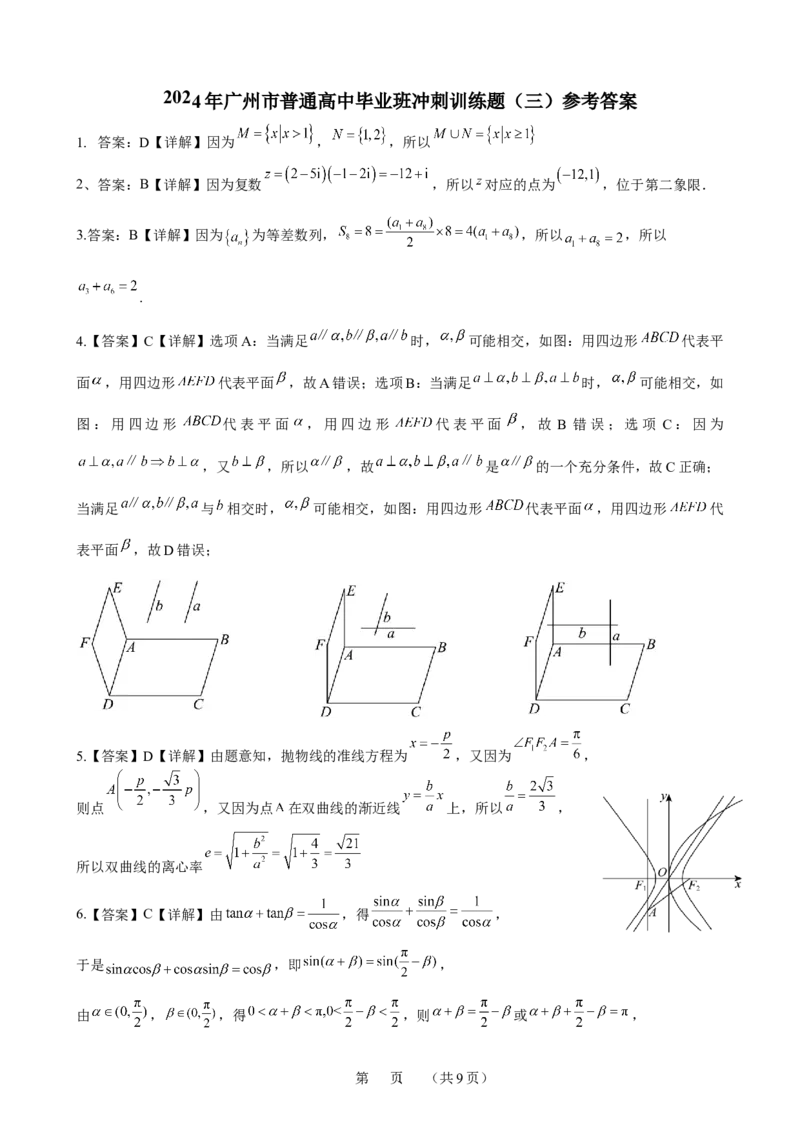
4.【答案】C【详解】选项A:当满足 时, 可能相交,如图:用四边形 代表平
面 ,用四边形 代表平面 ,故A错误;选项B:当满足 时, 可能相交,如
图:用四边形 代表平面 ,用四边形 代表平面 ,故 B 错误;选项 C:因为
,又 ,所以 ,故 是 的一个充分条件,故C正确;
当满足 与 相交时, 可能相交,如图:用四边形 代表平面 ,用四边形 代
表平面 ,故D错误;
5.【答案】D【详解】由题意知,抛物线的准线方程为 ,又因为 ,
则点 ,又因为点 在双曲线的渐近线 上,所以 ,
所以双曲线的离心率
6.【答案】C【详解】由 ,得 ,
于是 ,即 ,
由 , ,得 ,则 或 ,
第 页1 (共9页)即 或 (不符合题意,舍去),所以 .故选:C
7.【答案】D【详解】设正四面体 的棱长为 ,则其内切球、棱切球、外接球的半径分别为
.由题意知,球 的球心落在正四面体的几何中心,即内切球、棱切球、外接球公共
的球心,又球 的半径为定值 。当球 是正四面体 的外接球时,棱长 最小,此时
,得 .当球 是正四面体 的内切球时, 最大,此时 ,得
故正四面体 的棱长的取值范围为 .故选:D.
8.【答案】A【详解】由题意知,设 ,则 ,如图所示,
由 可得 ,
整理得 ,即 ,又因为 ,所以 ,
所以 ,所以 ,
在 中,由余弦定理得 ,所以 ,
由中线长公式,中线长 ,
9答案:BCD
10.答案:ACD【详解】对A:由题意可知 的定义域为 , ,
令 ,解得 ,当 时, ,当 时, ,故A正确;
对B:当 时, 取得极大值为 ,故B错误;
对C:由上分析可作出 的图象,要使方程 有两个不等实根,只需要 与 有两个交
点,由图可知, ,所以实数 的取值范围为 ,故C正确.
对D:设曲线 在 处的切线经过坐标原点,则切线斜率 ,解得
第 页2 (共9页), ,所以切线斜率 ,所以切线方程为 ,故D正确.
11.答案:ABD【详解】对于A,设点 在准线 上的投影为 ,准线 与 轴交于点 ,
又 , ,则 ,所以 ,故A正确;
对于B,设点 在准线 上的投影为点 ,易证 ,又 ,
,即 , , ,故B正确;
对于C,分两种情况:当点 都在第一象限,设 , ,
由焦半径公式可得 , , ,
令 ,
设 ,且 ,
,当且仅当 时取得最小值.
当点 在第二象限时,设 , ,
则 , ,所以 ,
同理令 ,且 ,
,
所以 ,当且仅当 时取得最小值,
综上, 面积的最小值为 ,故C错误;
第 页3 (共9页)对于D,当点 都在第一象限, , ,
则 ,所以 ,即 , ,
当点 在第二象限时,同理可得 ,即 , ,
综上, 的面积大于 ,故D正确. 故选:ABD.
12.【答案】20 【详解】由 ,
令 可得 , ,∴ .
在 中,令 ,可得 ,
∴
13.【答案】 【详解】根据题意,设甲获胜为事件 ,比赛进行三局为事件 ,
, ,
故
.
14.【答案】 【详解】不等式 ,即 ,
设 , ,
设 , ,所以 单调递增,且 , ,
所以存在 ,使 ,即 ,
当 时, , 单调递减,当 时, , 单调递增,
第 页4 (共9页)所以 ,
因为 ,所以 ,
当 时, ,当 时, ,
不等式 有整数解,即 有整数解,
若 时,即 ,因为函数 在 上单调递减,在 上单调递增,
所以 时, ,所以 无整数解,不符合题意,
当 时,因为 ,显然 是 的两个整数解,符合题意,
综上可知, .
15.【详解】(1)解:由题意知:数列 是公差为 的等差数列,
当 时, ,所以 ,整理得: , .................2分
又当 时, , ..................3分
因为 满足上式, ..................4分
所以 ,故数列 的通项公式为 ..................5分
(2)解:由(1)知 ,可得 , ..................6分
故 ; .................8分
解法1:由 ,可得 , ..................9分
第 页5 (共9页)即 ,则 , ..................10分
又由 , ..................12分
当且仅当 时取等号,故实数 的取值范围为 . ..................13分
解法2:由 , ..................9分
可得 , ..................10分
当 ,即 时, , ..................12分
则 ,故实数 的取值范围为 . ..................13分
16. ..................1分
, , , ..................2分
, .................3分
延长BC,AD,设BC的延长线和AD的延长线交点为M,连接PM,
则平面PAD和平面PBC的交线l为直线PM .................5分
证明:取AD的中点E,连接PE, ,E是AD的中点,
, 平面 平面 ABCD,平面 平面 , 平面 PAD,
, 平面ABCD, .................6
第 页6 (共9页)分
, ,即
.................7分
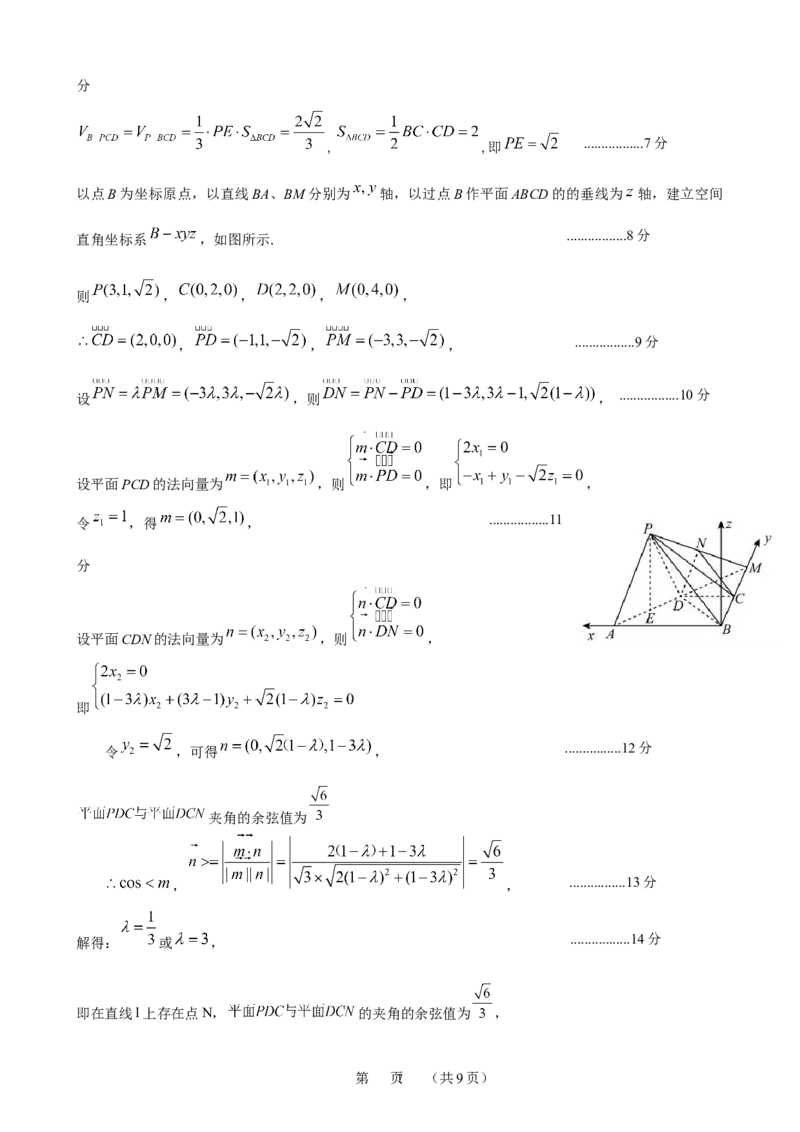
以点B为坐标原点,以直线BA、BM分别为 轴,以过点B作平面ABCD的的垂线为 轴,建立空间
直角坐标系 ,如图所示.
.................8分
则 , , , ,
, , ,
.................9分
设 ,则 ,
.................10分
设平面PCD的法向量为 ,则 ,即 ,
令 ,得 , .................11
分
设平面CDN的法向量为 ,则 ,
即
令 ,可得 ,
................12分
夹角的余弦值为
, ,
................13分
解得: 或 ,
.................14分
即在直线l上存在点N, 的夹角的余弦值为 ,
第 页7 (共9页)此时 或 .................15分
17、【详解】(1)设最低正常使用零下温度的第60百分位数为 ,
由直方图可知最低正常使用零下温度在 的频率为0.4,
在 的频率为0.65,因此最低正常使用零下温度的第60百分位数 一定在 内,..............1分
则有 ,解得 ,
所以最低正常使用零下温度的第60百分位数为28℃. ..................3分
(2)①由题意可知 的可能值是0,1,2,3, , .................5分
; ..................6分
; ..................7分
; .................8分
,
所以 的分布列为
0 1 2 3
0.064 0.288 0.432 0.216
..................9分
②由题意可知,设抽到 类锂电池的数量为 ,则 , .................10分
若抽到 块的可能性最大,
则 , , ..................12分
即 ..................13分
第 页8 (共9页)即 解得 , ..................14分
由于 ,故 . ..................15分
18、【详解】(1)解:设所求轨迹E上的任意点为(x,y),与x2+ y2=2对应的点为(x ,y ),
1 1
根据题意,可得¿,即¿,
2 2 x2
代入方程x2+ y2=2,可得x2+( y) =2,整理得 + y2=1,
√2 2
x2
所以曲线E的轨迹方程为 + y2=1. - ------5分
2
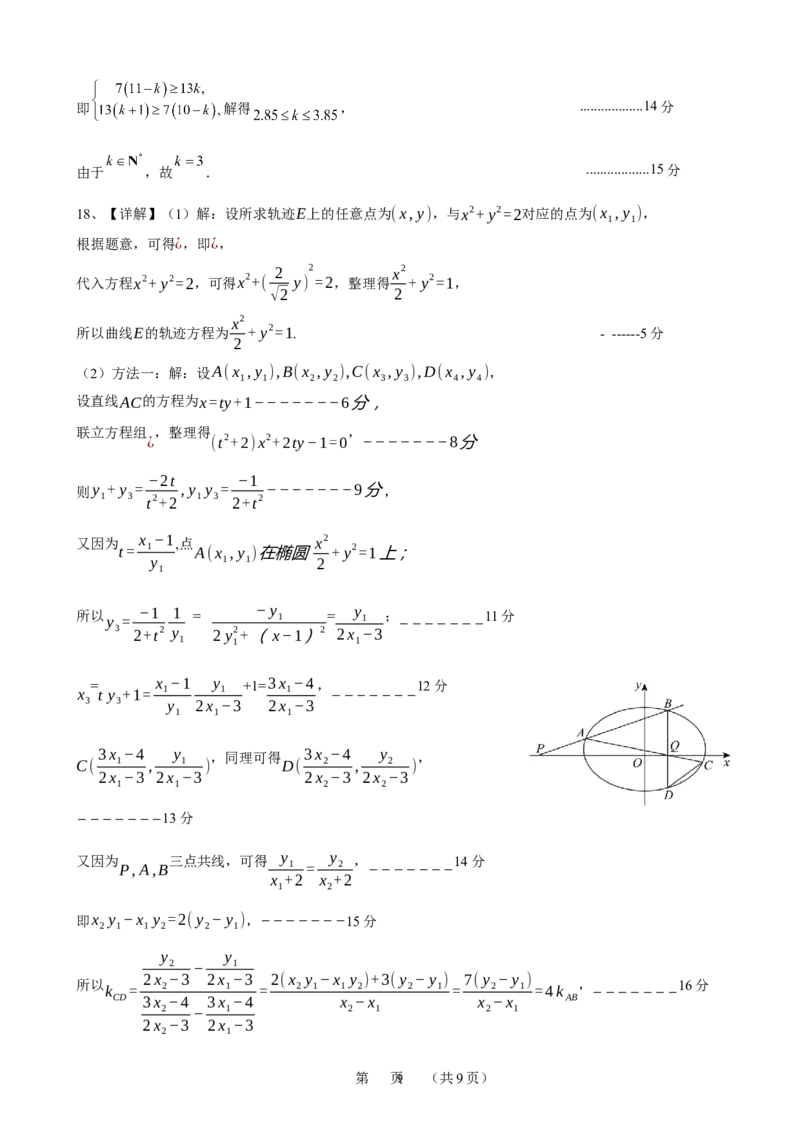
(2)方法一:解:设A(x ,y ),B(x ,y ),C(x ,y ),D(x ,y ),
1 1 2 2 3 3 4 4
设直线AC的方程为x=ty+1−−−−−−−6分,
联立方程组 ,整理得 ,
¿ (t2+2)x2+2ty−1=0 −−−−−−−8分
−2t −1
则y + y = ,y y = −−−−−−−9分,
1 3 t2+2 1 3 2+t2
又因为 x −1 ,点 x2
t= 1 A(x ,y )在椭圆 + y2=1上;
y 1 1 2
1
所以 y = −1 1 = −y 1 = y 1 ; −−−−−−− 11分
3 2+t2 y 2y2+(x−1)2 2x −3
1 1 1
= x −1 y +1=3x −4, 12分
x t y +1= 1 1 1 −−−−−−−
3 3 y 2x −3 2x −3
1 1 1
3x −4 y ,同理可得 3x −4 y ,
C( 1 , 1 ) D( 2 , 2 )
2x −3 2x −3 2x −3 2x −3
1 1 2 2
−−−−−−−13分
又因为 三点共线,可得 y y , 14分
P,A,B 1 = 2 −−−−−−−
x +2 x +2
1 2
即x y −x y =2(y −y ),−−−−−−−15分
2 1 1 2 2 1
y y
2 − 1
所以 k = 2x 2 −3 2x 1 −3 = 2(x 2 y 1 −x 1 y 2 )+3(y 2 −y 1 ) = 7(y 2 −y 1 ) =4k , −−−−−−− 16分
CD 3x −4 3x −4 x −x x −x AB
2 − 1 2 1 2 1
2x −3 2x −3
2 1
第 页9 (共9页)所以tanα k 1. 17分
= AB = −−−−−−−
tanβ k 7
CD
方法二:解:设直线AC的方程为y=k(x−1),A(x ,y ),B(x ,y ),C(x ,y ),D(x ,y ),
1 1 2 2 3 3 4 4
联立方程组 ,整理得 ,
¿ (1+2k2 )x2−4k2x+2k2−2=0
则 ,且
4k2 2k2−2,
Δ=(−4k2 ) 2−4(1+2k2 )(2k2−2)>0 x +x = ,x x =
1 3 1+2k2 1 3 1+2k2
可得3 2+4k2 ,所以 3x −4,
(x +x )−x x = =2 x = 1
2 1 3 1 3 1+2k2 3 2x −3
1
可得 y 3x −4 y ,
y = 1 ⋅( 1 −1)= 1
3 x −1 2x −3 2x −3
1 1 1
所以 3x −4 y ,下同方法一。
C( 1 , 1 )
2x −3 2x −3
1 1
19、【详解】(1)根据题意可知,不等式 在 上恒成立,
设 ,则 , ,
设 ,则 , ,则 ,
若 ,存在区间 ,使 在区间 上单调递减;
则 ,则 在区间 上单调递减,
则 ,不满足题意,故 ,即 .
下证明:当 时,不等式成立,因为 , ,
设 ,则 ,
设 ,则 ,所以 在 上单调递增,
则 ,则 成立,
故 在 上单调递增,则 ,所以 恒成立,得证,
第 页10 (共9页)综上知, . ..................5分
(2)当 时, ,设 ,
则 ,则函数 单调递增, , 单调递增,
, ,
在 上单调递减, 上单调递增,
又 , ,
, ,
, .
由于, , , ,
由于 在 上单调递增, .
累加得 . ..................11分
(3)要证 即证 .
即证 . ,设
, 时 , 在 上单调递增,即 在 上单调递增,
设 , ,
由于 在 上单调递增, , , 在 单调递增.
第 页11 (共9页)又 , 时
因此 恒成立,
原不等式恒成立,得证. ..................17分
第 页12 (共9页)