文档内容
数 学
2024. 8.
本试题卷共 4 页 ,19 题。全卷满分 150 分。考试用时 120 分钟。
祝考试顺利
★ ★
注意事项 :
1. 答题前 ,先将自己的姓名、准考证号填写在试卷和答题卡上 ,并将准考证号条形码
粘贴在答题卡上的指定位置。
2. 选择题的作答:每小题选出答案后 ,用 2B 铅笔把答题卡上对应题 目 的答案标号涂黑 。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3. 非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内 。写在试卷、
草稿纸和答题卡上的非答题区域均无效。
4. 考试结束后 ,请将本试卷和答题卡一并上交。
一、选择题 :本题共 8 小题,每小题 5 分 ,共 40 分。在每小题给出的四个选项中, 只有一项 是符
合题目要求的。
1. 已知 M,N 为全集 U 的非空真子集 ,且 M 与 N 不相等 ,若 ( M) ∩N= ,则 M∪N=
U
A. M B. N C. D. U ∁ ∅
2. 已知点 P 在抛物线 x2 = - 5y 上 ,且 A∅(0, - 3) ,则 PA 的最小值为
35
A. B. C. D.
2
3. 某地区想实行阶梯电价 ,经调查发现 ,该地区居民用电量信息如下 :
分位数 50% 分位数 70% 分位数 80% 分位数 90% 分位数
用电量 /(kW ·h) 160 176 215 230
如果要求约 70% 的居民用电量在第一阶梯内 ,约 20% 的居民用电量在第二阶梯内 ,可确
定第二阶梯电价的用电量(kW ·h) 范围为
A. (160,176] B. (176,215] C. (176,230] D. (230,+ ∞ )
数学试卷 第 1 页(共 4 页)
学科网(北京)股份有限公司4. 已知向量 a ≠ e, e = 1,对任意实数 t ,恒有 a - te ≥ a - e ,则
A. a ⊥ e B. e ⊥ a - e
C. a ⊥ a - e D. a + e ⊥ a - e
5. 把 8 个相同的篮球分发给甲、乙、丙、丁 4 人 ,不同的分发种数为
A. 70 B. 99 C. 110 D. 165
6. 设函数 若 f(x) 无最大值 ,则实数 a 的取值范围为
A. ( - ∞ , - 1) B. ( - ∞ , - 1] C. ( - ∞ ,2] D. ( - 1,2]
7. 当 x ∈ 时 ,曲线 y = cosx 与 y = 2cos 交点的个数为
A. 3 B. 4 C. 5 D. 6
8. 已知函数 f(n) = n - 1 + n - 2 + n - 3 + … + n - 20 ,其中 n 是自然数 ,则 f(n) 的最小值为
A. 50 B. 100 C. 110 D. 190
二、选择题 :本题共 3 小题,每小题 6 分 ,共 18 分。在每小题给出的选项中 ,有多项符合题 目要
求 ,全部选对的得 6 分 ,部分选对的得部分分 ,有选错的得 0 分。
9. 下列关于方程 4x2 + mx + 1 = 0(m ∈ R) 的结论中 ,正确的有
A. 方程的两根互为共轭复数
B. 若 m = 0,则方程两根互为相反数
C. 若 x 为方程的一个虚根 ,则 x 也为方程的根
D. 若 m < 0,则方程的两根一定都为正数
10. 设 A,B ,C,D 是空间中 4 个不同的点 ,在下列命题中正确的是
A. 若 AC 与 BD 共面 ,则 AD 与 BC 共面
B. 若 AC 与 BD 是异面直线 ,则 AD 与 BC 是异面直线
C. 若 AB = AC,DB = DC,则 AD = BC
D. 若 AB = AC,DB = DC,则 AD ⊥ BC
11. 已知数列{a } 是等差数列 ,{b } 是等比数列 ,则下列说法中正确的是
n n
A. 将数列{a } 的前 m 项去掉 ,其余各项依次构成的数列是等差数列
n
B. 数列 a + a + a ,a + a + a ,a + a + a , … ,是等差数列
1 2 3 4 5 6 7 8 9
C. 将数列{b } 的前 m 项去掉 ,其余各项依次构成的数列不是等比数列
n
D. 数列 bb ,bb ,bb ,bb , … ,是等比数列
1 2 2 3 3 4 4 5
数学试卷 第 2 页(共 4 页)
学科网(北京)股份有限公司三、填空题: 本题共 3 小题,每小题 5 分 ,共 15 分。
12. 已知 F ,F 是双曲线 的两个焦点 ,点 M 在 E 上 ,如果
1 2
MF F 的面积为 .
1 2
13. 已知函数 f(x) = x2 + 2x 和 g(x) = - x2 + a,如果直线 l 同时是 f(x) 和 g(x) 的切线 ,称 l 是 f(x) 和 g(x)
△
的公切线 ,若 f(x) 和 g(x) 有且仅有一条公切线 ,则 a = .
14. 将正整数数列 1,2,3,4,5, … 的各项按照上小下大、左小右大的原则写成如下的三角形
数表 :
将每行的第一个数与每行的最后一个数依次相加 ,前 n 行的和为 .
四、解答题 :本题共 5 小题,共 77 分。解答应写出文字说明、证明过程或演算步骤。
15. (13 分)
已知锐角 ABC 中 ,sin ,sin
(1) 求证:ta △ nA = 2tanB;
(2) 若 AB = 3,求 AB 边上的高.
16. (15 分)
已知椭圆的中心是坐标原点 O,它的短轴长为 2 2 ,一个焦点 F 的坐标为(c,0) (c > 0) ,
点 M 的坐标为 ,且 = 2 FM .
(1) 求椭圆的方程及离心率 ;
(2) 如果过点 M 的直线与椭圆相交于点 P,Q 两点 ,且 OP ⊥ OQ,求直线 PQ 的方程.
17. (15 分)
乒兵球单打决赛在甲、乙两名运动员间进行 ,比赛采用 7 局 4 胜制 ,假设两在每一局比
赛中获胜的可能性相等.
(1) 求甲以“4 :1”获胜的概率 ;
(2) 求乙获胜且比赛局数多于 5 局的概率 ;
(3) 求比赛局数的分布列.
数学试卷 第 3 页(共 4 页)
学科网(北京)股份有限公司18. (17 分)
设函数 f(x) = x3 + ax2 + bx + c.
(1) 若 a = - 3 ,b = c = 0 ,证明 : 曲线 f(x) 是中心对称图形 ;
(2) 若 a = b = 4 ,且函数 f(x) 有三个不同的零点 ,求实数 c 的取值范围 ;
(3) 证明 :“a2 - 3b > 0”是 f(x) 有三个不同的零点的必要不充分条件.
19. (17 分)
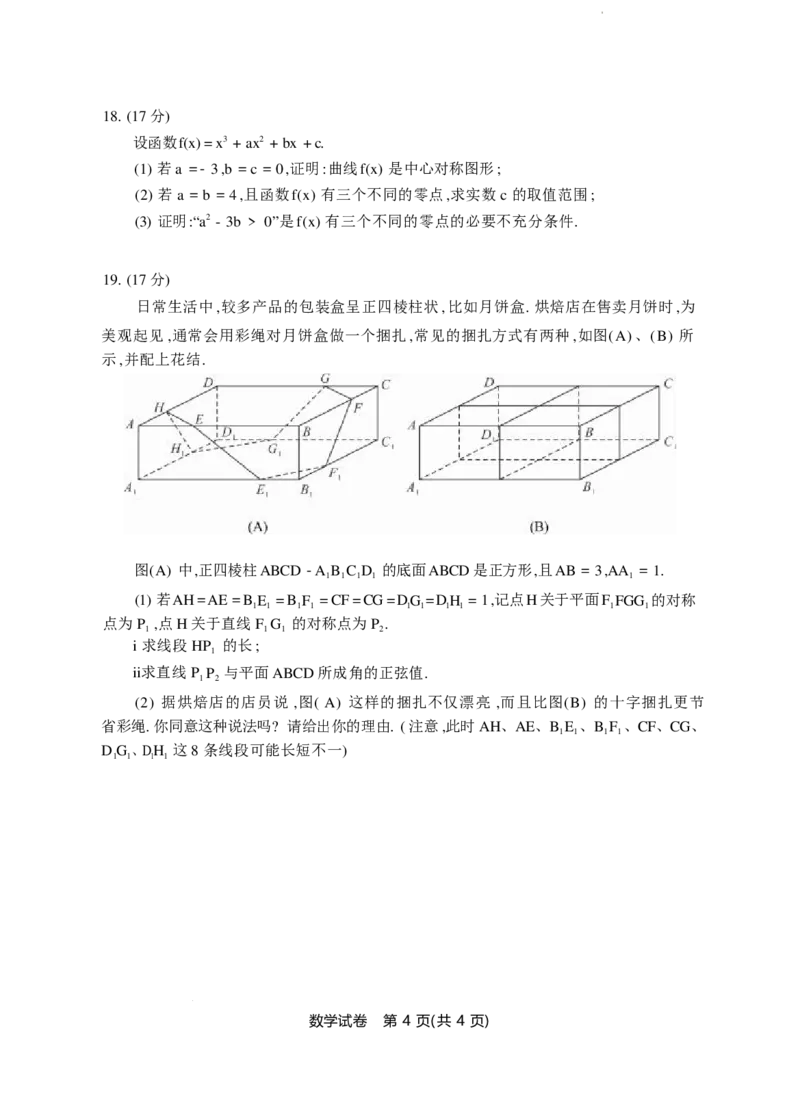
日常生活中 ,较多产品的包装盒呈正四棱柱状 , 比如月饼盒. 烘焙店在售卖月饼时 ,为
美观起见 ,通常会用彩绳对月饼盒做一个捆扎 ,常见的捆扎方式有两种 ,如图( A) 、( B) 所
示 ,并配上花结.
图( A) 中 ,正四棱柱 ABCD - A B C D 的底面 ABCD 是正方形 ,且 AB = 3 ,AA = 1.
1 1 1 1 1
(1) 若 AH = AE = B E = B F = CF = CG = DG = DH = 1 ,记点 H 关于平面 F FGG 的对称
1 1 1 1 1 1 1 1 1 1
点为 P ,点 H 关于直线 F G 的对称点为 P .
1 1 1 2
i 求线段 HP 的长 ;
1
ii求直线 P P 与平面 ABCD 所成角的正弦值.
1 2
(2) 据烘焙店的店员说 ,图( A) 这样的捆扎不仅漂亮 ,而且比图(B) 的十字捆扎更节
省彩绳. 你同意这种说法吗? 请给出你的理由. ( 注意 ,此时 AH、AE、B E 、B F 、CF、CG、
1 1 1 1
D G、DH 这 8 条线段可能长短不一)
1 1 1 1
数学试卷 第 4 页( 共 4 页)
学科网(北京)股份有限公司