湖北省重点高中智学联盟2025届新高三8月联考考试（8.15-8.16）数学试卷修改2.0版答案_8月_240818湖北省重点高中智学联盟2025届新高三8月联考考试

2025 届高三年级八月智学联考数学答案详解 1.【答案】B 【详解】解不等式x2x20，得1 x2，即A1,2，函数 yln(x1)有意义，得x10，解得 x1，则B(1,)， ð B ,1 ，所以Að B 1,1 ．故选：B． R R 2.【答案】A 1z i 【详解】因为 1i，所以1zzi1i，即2izi，所以z zi 2i  i  2i  1 2 1 2    i，所以z对应的点的坐标为 , ，位于第一象限．故选：A．  2i  2i  5 5 5 5 3.D          【分析】对|ab||a2b|两边平方化简可得 b 2 2ab0 ，再对|ab|平方化简后再开方即可.             【详解】由|ab||a2b|两边平方得， a 2 b 2 2aba 2 4b 2 4ab ，             所以 b 2 2ab0 ，所以|ab|2 a 2 b 2 2ab|a|29 ，所以|ab|3，故选：D. 4.【答案】D n  1 【详解】易知n8， m x   (m0)的展开式的二项式系数之和2n m1n ,m3，则  x  3 x  1  n   3x 1 2 x1   8 展开式的通项公式：Cr   3x 1 2   8r   x1r Cr38r(1)r x 8 2 3r  x   8   8 83r 1 令 5,r 6，所以 的系数为C632 252. 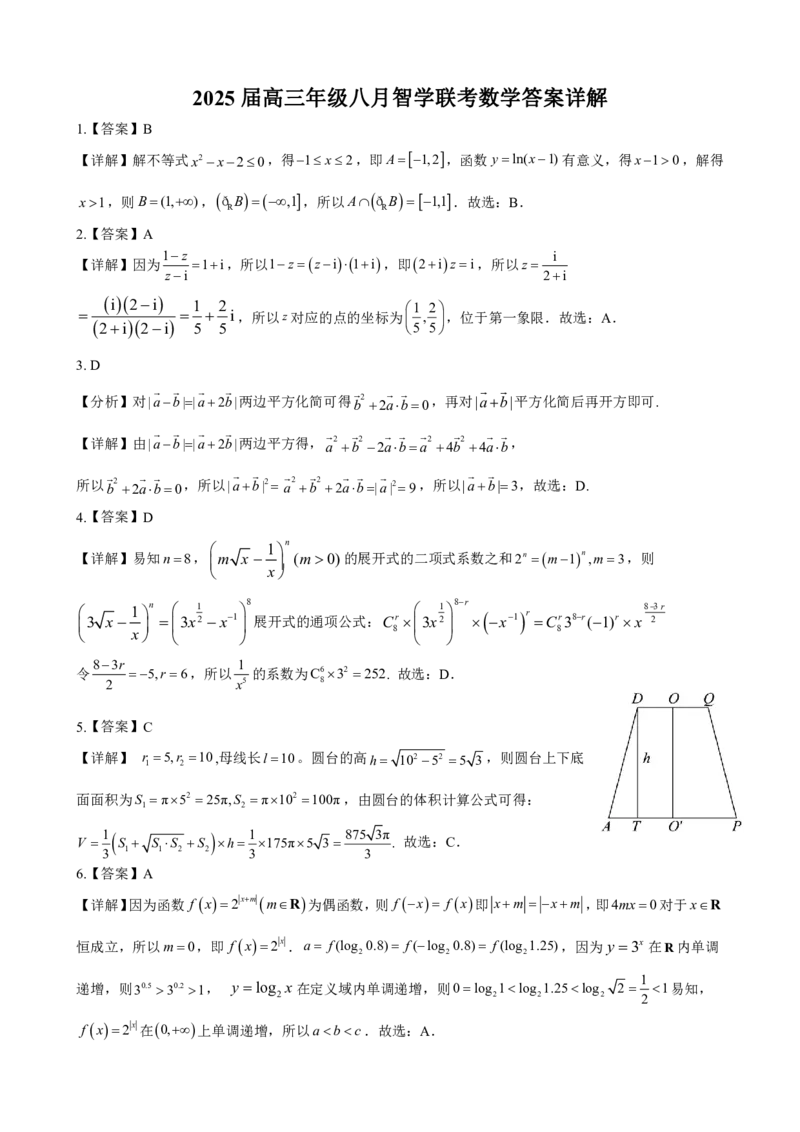故选：D． 2 x5 8 5.【答案】C 【详解】 r 5,r 10,母线长l 10。圆台的高 h 10252 5 3 ，则圆台上下底 1 2 面面积为S π52 25π,S π102 100π，由圆台的体积计算公式可得： 1 2 1  1 875 3π V  S  S S S h 175π5 3 . 故选：C． 3 1 1 2 2 3 3 6.【答案】A 【详解】因为函数 f x2xmmR为偶函数，则 f x f x即 xm  xm ，即4mx0对于xR 恒成立，所以m0，即 f x2x．a f(log 0.8) f(log 0.8) f(log 1.25)，因为 y 3x在R内单调 2 2 2 1 递增，则30.5 30.2 1， y log x在定义域内单调递增，则0log 1log 1.25log 2  1易知， 2 2 2 2 2 f x2x在0,上单调递增，所以abc．故选：A． {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#}7.【答案】C  π 【详解】 f(x)2cos2xsin2x1cos2xsin2x 2sin2x ，因为 f x的图象关于直线  4 π  π  π π π π π 3 x 轴对称，所以 f   2sin   2，故  kπ+ ,kZ，即6k ,kZ，当 12 12  6 4 6 4 2 2 π π 3π kπ  π 2x  2kπ，即x  ,kZ时，函数 f x取得最小值，因为 f x在0, 上没有最小值， 4 2 8   3 5π π 15 3 15 1 3 所以  ，即 ，由6k  ，解得k  ，故k0，得 . 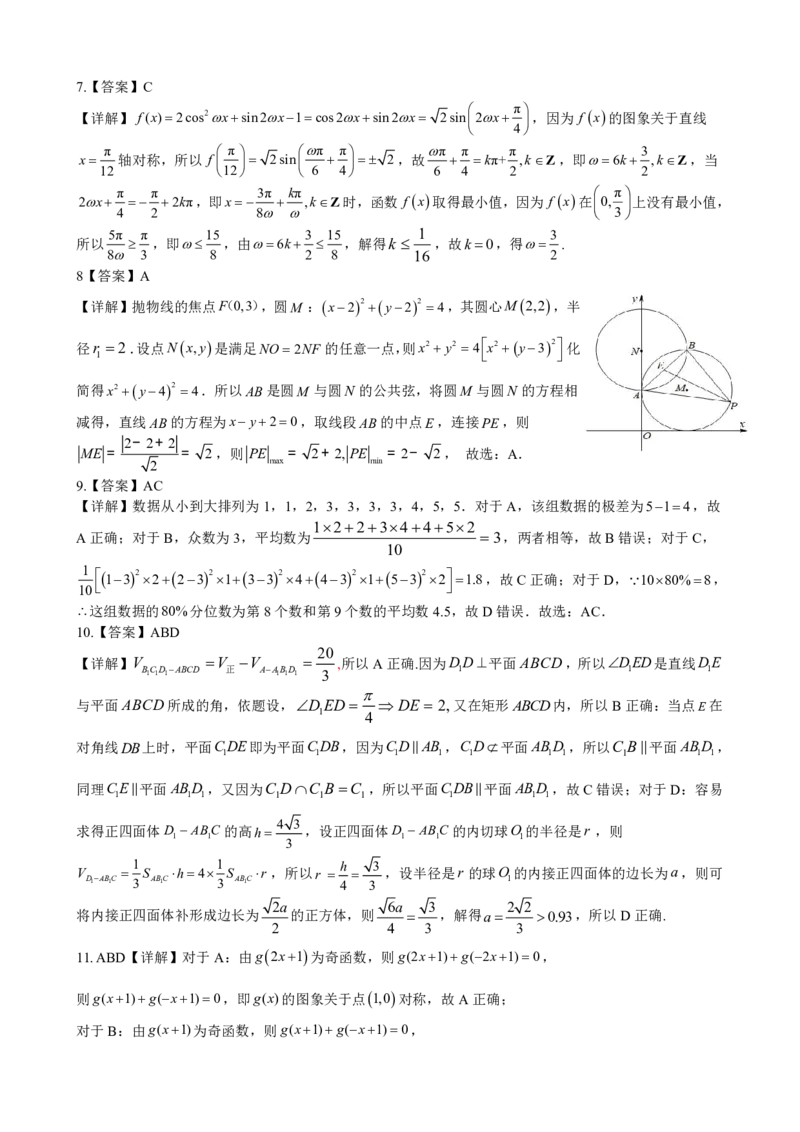8 3 8 2 8 16 2 8【答案】A 【详解】抛物线的焦点F（0,3），圆M ：x22y22 4，其圆心M2,2，半 径r 2．设点Nx,y是满足NO2NF 的任意一点，则x2y2 4x2y32 化 1   简得x2y42 4．所以AB是圆M 与圆N 的公共弦，将圆M 与圆N 的方程相 减得，直线AB的方程为xy20，取线段AB的中点E，连接PE，则 2- 2+ 2 ME = = 2，则 PE = 2+ 2, PE = 2- 2， 故选：A． 2 max min 9.【答案】AC 【详解】数据从小到大排列为1，1，2，3，3，3，3，4，5，5．对于A，该组数据的极差为514，故 12234452 A正确；对于B，众数为3，平均数为 3，两者相等，故B错误；对于C， 10 1 13222321332443215322 1.8，故C正确；对于D，1080%8，   10 这组数据的80%分位数为第8个数和第9个数的平均数4.5，故D错误．故选：AC． 10.【答案】ABD 20 【详解】V V V  ,所以A正确.因为DD平面ABCD，所以DED是直线DE B 1 C 1 D 1 ABCD 正 AA 1 B 1 D 1 3 1 1 1  与平面ABCD所成的角，依题设，DED   DE  2,又在矩形ABCD内，所以B正确：当点E在 1 4 对角线DB上时，平面CDE即为平面CDB，因为CDAB ，CD平面ABD ，所以C B平面ABD ， 1 1 1 1 1 1 1 1 1 1 同理CE平面ABD ，又因为C DC B C ，所以平面CDB平面ABD ，故C错误；对于D：容易 1 1 1 1 1 1 1 1 1 4 3 求得正四面体D ABC的高h ，设正四面体D ABC的内切球O 的半径是r ，则 1 1 1 1 1 3 1 1 h 3 V  S h4 S r ，所以r   ，设半径是r 的球O 的内接正四面体的边长为a，则可 D1 AB1C 3 AB1C 3 AB1C 4 3 1 2a 6a 3 2 2 将内接正四面体补形成边长为 的正方体，则  ，解得a 0.93，所以D正确. 2 4 3 3 11.ABD【详解】对于A：由g2x1为奇函数，则g(2x1)g(2x1)0， 则g(x1)g(x1)0，即g(x)的图象关于点1,0对称，故A正确； 对于B：由g(x1)为奇函数，则g(x1)g(x1)0， {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#}即得 f(x1) f(x1)c,c为常数，令x0，即得 f(1) f(1)c，则c=0， 故 f(x1) f(x1)0，即 f(x) f(2x)0，则 f(x2) f(4x)0， 又 f x2为奇函数，所以 f x2 f x20， 即 f(x) f(4x)0，可得 f(x2)f(x)，故 f(x2)f(2x)， 故 f(x)f(x)，即 f x f x0，即 f(x)是奇函数，故B正确； 对于C：由于 f(x) f(4x)0，故 f(4x)f(x) f(x)，即 f(4x) f(x)， 故4是 f(x)的一个周期， 又 f(x) f(4x)0，即g(x) g(4x)，所以gx为周期为4的周期函数， 因为g(2x1)g(2x1)0，所以g1g10，即g10， 所以g2025g45061g10，故C错误； 对于D：因为 f(x)是R上的奇函数，故 f(0)0， f(1)1，结合 f(x) f(2x)0得 f(2)0， f(3) f(23) f(1)f(1)1， f(4) f(0)0， 2024 故 f(k)506  f(1) f(2) f(3) f(4)  0，故D正确. 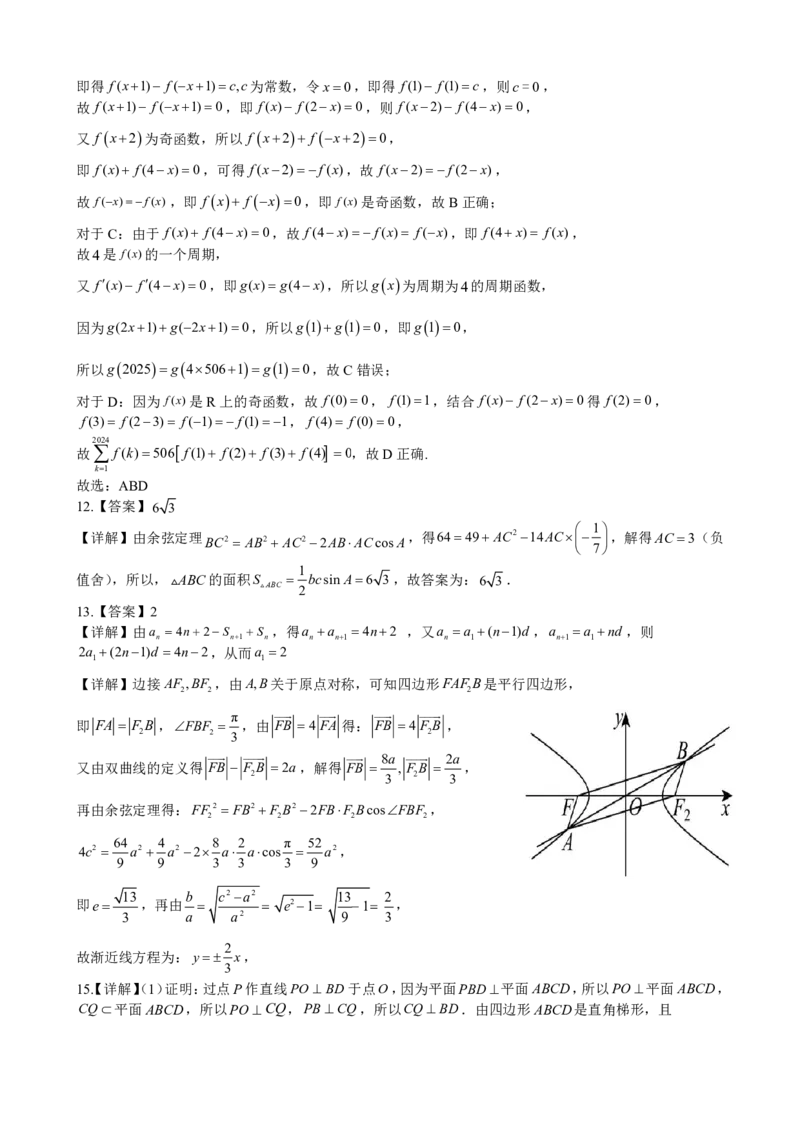k1 故选：ABD 12.【答案】6 3  1 【详解】由余弦定理 BC2  AB2AC22ABACcosA ，得6449AC214AC ，解得AC3（负  7 1 值舍），所以，ABC的面积S  bcsinA6 3，故答案为：6 3． ABC 2 13.【答案】2 【详解】由a 4n2S S ，得a a 4n2 ，又a a (n1)d，a a nd，则 n n1 n n n1 n 1 n1 1 2a (2n1)d 4n2，从而a 2 1 1 【详解】边接AF ,BF ，由A,B关于原点对称，可知四边形FAFB是平行四边形， 2 2 2 π     即 FA  F B ，FBF  ，由 FB 4FA 得： FB 4F B ， 2 2 3 2    8a  2a 又由双曲线的定义得 FB  F B 2a，解得 FB  , F B  ， 2 3 2 3 再由余弦定理得：FF2 FB2F B22FBF BcosFBF ， 2 2 2 2 64 4 8 2 π 52 4c2  a2 a22 a acos  a2， 9 9 3 3 3 9 13 b c2a2 13 2 即e ，再由   e21 1 ， 3 a a2 9 3 2 故渐近线方程为：y x， 3 15【. 详解】（1）证明：过点P作直线PO BD于点O，因为平面PBD平面ABCD，所以PO平面ABCD， CQ平面ABCD，所以PO CQ，PBCQ，所以CQBD．由四边形ABCD是直角梯形，且 {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#}π AB 3,BC2AD2,ABBC．在直角△ABD中， BD AB2AD2 2 ，可得DC 2,BCD ， 3   从而△BCD是等边三角形，CQBD， CBD ，所以BCQ ．从而 3 6  2 3 3 BQBCtanBCQ2tan  ，AQ ABBQ ，所以AQ:QB1:2···················5分 6 3 3 （2）解：因为PBPD，所以O是BD的中点，连接OC． 因为平面PBD平面ABCD，平面PBD平面ABCDBD，所以PO平面ABCD， 1 1 3 3 3 3 V  S PO  PO ，所以PO3． PABCD 3 ABCD 3 2 2 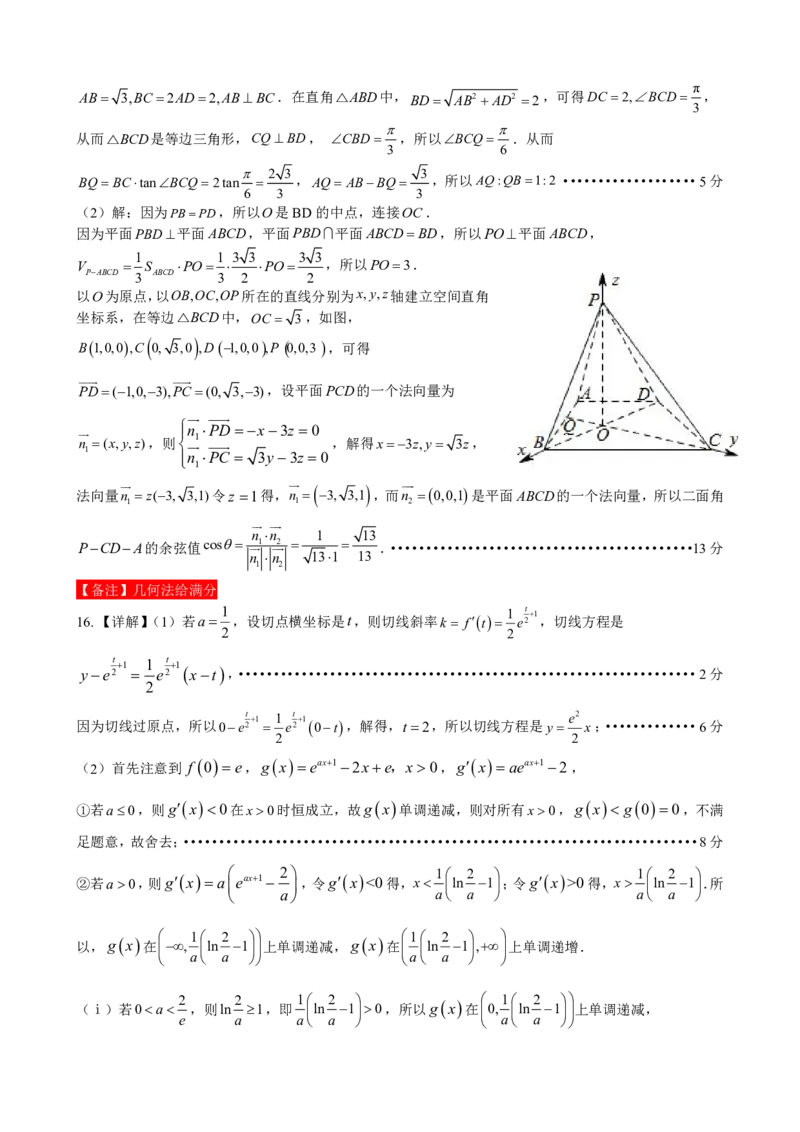以O为原点，以OB,OC,OP所在的直线分别为x,y,z轴建立空间直角 坐标系，在等边△BCD中，OC  3，如图， B1,0,0,C  0, 3,0  ,D 1,0,0,P 0,0,3 ，可得   PD(1,0,3),PC(0, 3,3)，设平面PCD的一个法向量为     n PD x3z  0 n (x,y,z)，则 1  ，解得x3z,y 3z， 1 n PC  3y3z 0 1 法向量n   z(3, 3,1)令z 1得，n    3, 3,1  ，而n  0,0,1是平面ABCD的一个法向量，所以二面角 1 1 2   n n 1 13 PCDA的余弦值cos 1 2   ．···········································13分 n n 131 13 1 2 【备注】几何法给满分 16.【详解】（1）若a 1 ，设切点横坐标是t，则切线斜率k  ft 1 e2 t 1，切线方程是 2 2 ye2 t 1  1 e2 t 1 xt ，·································································2分 2 因为切线过原点，所以0e2 t 1  1 e2 t 10t，解得，t2，所以切线方程是y e2 x；·············6分 2 2 （2）首先注意到 f  0 e，g  x eax12xe，x 0，g x aeax12， ①若a0，则g x 0在x0时恒成立，故g  x  单调递减，则对所有x0，g  x  g  0 0，不满 足题意，故舍去；·········································································8分  2 1 2  1 2  ②若a0，则g x aeax1 ，令g x  <0得，x ln 1；令g x  >0得，x ln 1．所  a a a  a a   1 2  1 2   以，g  x  在, ln 1上单调递减，g  x  在 ln 1,上单调递增．  a a  a a   （ⅰ）若0a 2 ，则ln 2 1，即 1 ln 2 1  0，所以g  x  在  0, 1 ln 2 1    上单调递减， e a a a   a a  {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#}1 2   1 2   ln 1,上单调递增，则g  x   f  ln 1  f  0  0不满足题意，故舍去； a a   min a a  （ⅱ）若a 2 ，则ln 2 1，即 1 ln 2 1  0，所以g  x  在0,上单调递增，则对所有x0， e a a a  g  x  f  0 0，符合题意． 2  综上所述，a的取值范围是  ,．······················································15分 e  【备注】用切线放缩做，只要过程严谨，给满分. 1 17.【详解】（1）由题意PX 305 1PX 1 10.68270.84135，若某天该商场有200 2 位顾客，估计该天消费额X 在305，内的人数为0.84135200168.27168；··················6分  3  3 1 （2）设X的取值为0，10，20，则P(X 0)  1   1   ，  4  4 16 3 1 1 1 3 1 1 5 5 P(X 10)        ，P(X 2)1P(X 0)P(X 1) ，·······13分 4 3 3 4 4 3 3 48 6 所以X的分布列为 X 0 10 20 1 5 5 P 16 48 6 1 5 5 425 数学期望E(X)0 10 20  ．··············································15分 16 48 6 24 425 【备注】第二问，讨论A为一类或二类给满分，只要最终结果出现 就行. 24 ac1  17.【详解】（1）由椭圆上的点到焦点的最近距离是1，故ac1，则 a2b2  7，解得a2，b 3，  a2 b2c2  x2 y2 c1，即椭圆E的方程为  1；·······················································5分 4 3 y y y y （2）设Bx 1 ，y 1 、Cx 2 ,y 2 ，由题可知，A2，0，则k 1  x  1 2 ，k 2  x  2 2 ，所以k 1 k 2  xx 2 1 x 2 x 4 1 2 1 2 1 2 ykx4 ①.由题意，设BC所在的直线方程为ykx4，联立  x2 y2 可得，  34k2 x232k2x64k2120，   1  4 3 且  32k22 4  4k23  64k212  0 ， 1 32k2 64k212 解得0 k  依据韦达定理，x x  ，x x  ，······························7分 2 1 2 34k2 1 2 34k2 y y 设直线AB的方程为y 1 x2 ，直线AC的方程为y 2 x2 ， x 2 x 2 1 2 {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#} 6y   6y  则依题设，M4， 1 、N4， 2 ，y kx 4，y kx 4，则  x 2  x 2 1 1 2 2 1 2 6y 6y 6yx 12y 6y x 12y 36kx 36k x x MN  1  2  1 2 1 2 1 2  1 2  36k  1 2 ，10分 x 2 x 2 xx 2x x 4 xx 2x x 4 xx 2x x 4 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1024k4 256k2 48  x x 2 4xx  34k2 34k2 即 MN  36k  1 2 1 2  36k  ，化简得 xx 2x x 4 144k2 1 2 1 2 34k2 144576k2 14k2 1 MN  36k  3 3 4，··········································14分 144k2 k2 k2 1 1 1 依题设， MN 3 4 3 5，所以k  ，满足0 k  合题意．·························16分 k2 3 2 1 综上所述，直线的斜率k  ．···························································17分 3 【备注】不检验扣一分. 19.【详解】（1）a 有三种结果： 1，1，2，2或1，2，2，2或1，2，4，2；···················4分 n a a a （1）当m2025时，n2,3,,2024．由a 1,1 2 2,,1 n1 2,1 n 2， 1 a a a 1 n2 n1 累乘得1a 2n1①；·····································································5分 n a a a a 又由1 n 2,，1 n1 2,,1 2023 2,1 2024 2,1a a ， a a a a 2025 2025 n1 n2 2024 2025 累乘得1a 22025na ②；·······························································6分 n 2025 将①②相乘得1a2 22024a ，又a N*，a 16，所以1a 21014. ·······················7分 n 2025 n 2025 n 所以数列a 的最大项的最大值为21014，满足条件的数列为 n  2n1 n1,2,,1015 a  ；······················································9分 n 22029n n1016,1017,,2025 （3）①讨论项数满足1  k  M 的情况： a 因为数列{a }满足：当1nM 1时1 n1 2，a 1，所以0a 2， n a 1 2 n 又因为当1iM 1，都有a N，所以a 1或a 2，·····································10分 i 2 2 当a 2时，a a 2，此时a a 2a a ，这与在剩下的项中总存在满足1 pqM 的项a 和a ， 2 4 3 1 2 3 4 p q 使得a a a a 矛盾，所以a 1，类似的，必有a 1，a 1，a 2，a 2，················12分 s t p q 2 3 4 5 6 由a a a a 得前6项任意两项之积小于等于4时，均符合，要使得m值要尽量小，则需要每项尽可能 s t p q {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#}大，且则a a 4a a ，a 22， 5 6 1 7 7 同理，a 23，a 24，，a 22023，由对称性得最后6项为a a a a 22025， 8 9 M6 M M1 M2 M3 a a 22024，······································································14分 M4 M5 当{a }中间各项为公比为2的等比数列时，可使得M值最小，且M的最小值为M 6202262034， n min 满足已知条件． ②讨论项数满足M k m的情况： 类比①可知a a  a  a 22025，a a 22024，a 22023，a 22022，，a 23， M M1 M2 M3 M4 M5 M6 M7 m7 a 22，a 2，a 2，a a a a 20 1．······························16分 m6 m5 m4 m3 m2 m1 m 综上所述，m的最小值m 2034214067．故答案为：4067．······························17分 min 【备注】1.第一问多写一种情况扣一分；2.第二问不给出数列的构造不扣分；3.计数错了，但是过程正确， 酌情扣分； {#{QQABIQCEogAIAIBAABgCAQnKCAIQkBCCAQgGgFAIMAAAAAFABCA=}#}