文档内容
邵阳市第二中学 2022 级高三第一次月考数学试卷
时间:120分钟 满分:150分
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的)
1. 若非空集合A,B满足 ,U为全集,则下列集合中表示空集的是( )
A. ; B. ; C. ; D. .
2. sin40°(tan10°-√3)=
A. - B. -1 C. D. -
3. 已知函数 的定义域是 ,则函数 的定义域为( )
A. B.
C. D.
4. 下列求导数计算错误的是( )
A. B.
C. D.
5. 苏格兰数学家纳皮尔(J. Napier,1550-1617)发明的对数及对数表(如下表),为当时的天文学家处
理“大数”的计算大大缩短了时间.即就是任何一个正实数N可以表示成 ,则
,这样我们可以知道N的位数.已知正整数 是35位数,则M的值为(
)
N 2 3 4 5 11 12 13 14 15
.
0.30 0.48 0.60 070 1.04 1.08 1.11 1.15 1.18
第1页/共6页
学科网(北京)股份有限公司A. 3 B. 12 C. 13 D. 14
的
6. 一家商店使用一架两臂不等长 天平称黄金.一位顾客到店里购买 黄金,售货员先将 的砝码放
在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将 的砝码放在天平右盘中,再取出一些黄
金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.你认为顾客购得的黄金( )
为
附:依据力矩平衡原理,天平平衡时有 ,其中 、 分别 左、右盘中物体质量, 、
分别为左右横梁臂长.
A. 等于 B. 小于 C. 大于 D. 不确定
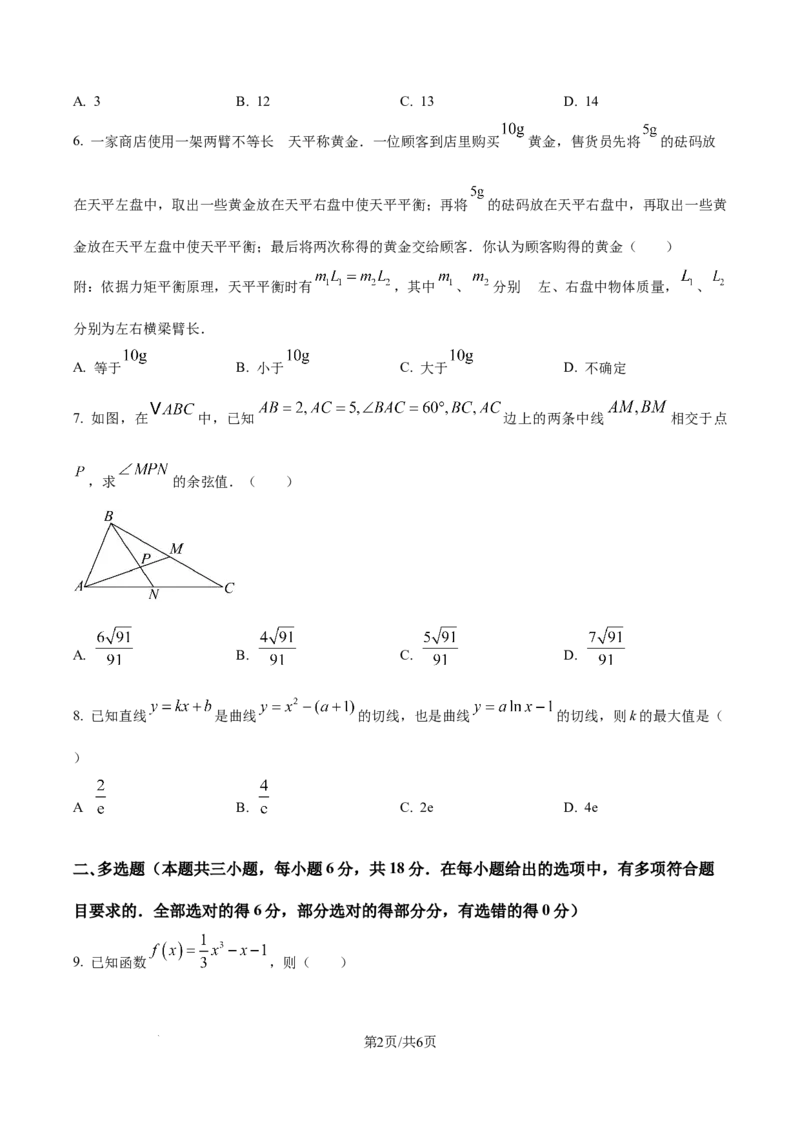
7. 如图,在 中,已知 边上的两条中线 相交于点
,求 的余弦值.( )
A. B. C. D.
8. 已知直线 是曲线 的切线,也是曲线 的切线,则k的最大值是(
)
.
A B. C. 2e D. 4e
二、多选题(本题共三小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 已知函数 ,则( )
第2页/共6页
学科网(北京)股份有限公司A. 有一个零点 B. 的极小值为
C. 的对称中心为 D. 直线 是曲线 的切线
10. 设点D是 所在平面内一点,O是平面上一个定点,则下列说法正确的有( )
A. 若 ,则D是BC边上靠近B的三等分点
B. 若 ,( 且 ),则直线AD经过 垂心
的
C. 若 ,且x, , ,则 是 面积的一半
D. 若平面内一动点P满足 ,( 且 ),则动点P的轨迹一定通过
的外心
11. 设函数 向左平移 个单位长度得到函数 ,已知 在 上有且
只有5个零点,则下列结论正确的是( )
A. 的图象关于直线 对称
B. 在 上,方程 的根有3个,方程 的根有2个
C. 在 上单调递增
D. 的取值范围是
三、填空题(本大题共3小题,每小题5分,共15分)
12. 出入相补是指一个平面(或立体)图形被分割成若干部分后面积(或体积)的总和保持不变,我国汉
代数学家构造弦图,利用出入相补原理证明了勾股定理,我国清代的梅文鼎、李锐、华蘅芳、何梦瑶等都
第3页/共6页
学科网(北京)股份有限公司通过出入相补原理创造了不同的面积证法证明了勾股定理.在下面两个图中,若 , ,
,图中两个阴影三角形的周长分别为 , ,则 的最小值为________.
13. 某时钟的秒针端点A到中心点O的距离为 ,秒针均匀地绕点O旋转,当时间 时,点A与钟
面上标12的点B重合,将A,B两点的距离 表示成 的函数,则 ______ 其中 .
14. 如图,在边长为1的正方形 中, 为 的中点, 点在正方形内(含边界),且 .
①若 ,则 的值是_______;②若向量 ,则 的最小值为
________.
四、解答题(本题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤)
15. 在 中,内角 的对边分别为a,b,c,且 .
第4页/共6页
学科网(北京)股份有限公司(1)求 的值;
(2)若 ,点 是线段 上的一点, , ,求 的值.
16. 如图所示,正方形 与矩形 所在平面互相垂直, ,点 为 的中点.
(1)求证: 平面 ;
(2)在线段 上是否存在点 ,使二面角 的平面角的大小为 ?若存在,求出 的
长;若不存在,请说明理由.
17. 已知函数 ,其导函数为 .
(1)若 在 不是单调函数,求实数 的取值范围;
(2)若 在 恒成立,求实数 的最小整数值.
18. 已知函数
(1)当 时,求 的单调增区间;
(2)若 ,使 ,求实数a的取值范围.
19. 如果数列 满足: 且 则称
为n阶“归化”数列.
(1)若某3阶“归化”数列 是等差数列,且单调递增,写出该数列的各项;
(2)若某11阶“归化”数列 是等差数列,求该数列的通项公式;
第5页/共6页
学科网(北京)股份有限公司(3)若 为n阶“归化”数列,求证
第6页/共6页
学科网(北京)股份有限公司