2024选填压轴解题技巧（学生版）(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024年新高考选填压轴解题技巧

2024新高考选填压轴解题技巧 专题一 函数性质相关解题技巧2 技巧1 函数单调性的应用及解题技巧 2 技巧2 函数奇偶性的应用及解题技巧 3 技巧3 函数周期性的应用及解题技巧 6 技巧4 函数对称性的应用及解题技巧 7 技巧5 函数4大性质的综合应用及解题技巧10 技巧6“奇函数+常函数”的最大值+最小值解题技巧11 技巧7“奇函数+常函数”的f(a)+f(-a)解题技巧14 技巧8 已知函数解析式判断函数图象解题技巧15 技巧9 已知函数图象判断函数解析式解题技巧21 专题二 函数值比较大小解题技巧24 技巧1 构造函数比较函数值大小关系解题技巧24 技巧2 两类经典超越不等式比较函数值大小关系解题技巧26 技巧3 泰勒不等式比较函数值大小关系解题技巧28 技巧4 不等式放缩合集比较函数值大小关系解题技巧31 专题三 函数选填压轴题解题技巧35 技巧1 函数对称性的应用及解题技巧35 技巧2 解不等式(含分段函数)的应用及解题技巧36 技巧3 整数解的应用及解题技巧37 技巧4 零点的应用及解题技巧41 技巧5 切线与公切线的应用及解题技巧45 专题四 导数综合问题解题技巧48 技巧1 端点效应(必要性探路)解题技巧 48 技巧2 函数凹凸性解题技巧55 技巧3 洛必达法则解题技巧59 专题五 不等式相关解题技巧 63 技巧1 基本不等式链的应用及解题技巧63 技巧2 权方和不等式的应用及解题技巧65 技巧3 普通型糖水不等式的应用及解题技巧67 技巧4 对数型糖水不等式的应用及解题技巧69 专题六 三角恒等变换解题技巧70 技巧1 拼凑思想的应用及解题技巧70 技巧2 升(降)幂公式的应用及解题技巧72 技巧3 三倍角公式的应用及解题技巧74 技巧4 半角公式的应用及解题技巧75 技巧5 万能公式的应用及解题技巧76 技巧6 正余弦平方差公式的应用及解题技巧77 专题七 平面向量解题技巧 78 技巧1“爪子定理”的应用及解题技巧78 技巧2 系数和(等和线)的应用及解题技巧80 技巧3 极化恒等式的应用及解题技巧86 技巧4 奔驰定理与三角形四心的应用及解题技巧87 专心 专注 专业 第 页 共 页 1 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~ ~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~ ~~~~~~~~~~~~ 专题一 函数性质相关解题技巧 技巧1 函数单调性的应用及解题技巧 在考查函数单调性时，如果能掌握同一定义域内，单调性的运算，可以快速判断函数的单调性；同时复 合函数单调性的相关计算也是高考重点，常以小题形式考查. 知识在线 1.同一定义域内 ①增函数(↗)+增函数(↗)=增函数↗ ②减函数(↘)+减函数(↘)=减函数↘ 1 ③f(x)为↗，则-f(x)为↘， 为↘ f(x) ④增函数(↗)-减函数(↘)=增函数↗ ⑤减函数(↘)-增函数(↗)=减函数↘ ⑥增函数(↗)+减函数(↘)=未知(导数) 2.复合函数的单调性 函数f(x)=h gx ~ ~ ~ ~    ，设u=gx  ，叫做内函数，则f(x)=hu  叫做外函数， 内函数↑，外函数↑，⇒复合函数↑  内函数↓，外函数↓，⇒复合函数↑ ⇒结论：同增异减  内函数↑，外函数↓，⇒复合函数↓   内函数↓，外函数↑，⇒复合函数↓ 1 【典例1】(2020·全国·统考高考真题)设函数f(x)=x3- ,则f(x) ( ) x3 A. 是奇函数，且在0，+∞  单调递增 B. 是奇函数，且在0，+∞  单调递减 C. 是偶函数，且在0，+∞  单调递增 D. 是偶函数，且在0，+∞  单调递减 【典例2】(2023·宁夏银川·统考模拟预测)已知函数fx  2 =1- ，则 ( ) 2x+1 A. fx  是偶函数且是增函数 B. fx  是偶函数且是减函数 C. fx  是奇函数且是增函数 D. fx  是奇函数且是减函数 【典例3】(2023·全国·模拟预测)函数fx  =log -x2+x+6 1 3  的单调递减区间为 ( ) 1 A. -2, 2  1 B. -∞, 2  1 C.  ,+∞ 2  1 D.  ,3 2  技巧2 函数奇偶性的应用及解题技巧 纵观历年考题，函数奇偶性是函数及高考的重要考点，要熟悉奇偶性的定义，若能熟悉奇偶性的运算， 则可提升解题速度，做到快速求解. 知识在线 ①具有奇偶性的函数定义域关于原点对称(大前提) ②奇偶性的定义： 奇函数：f-x  =-f(x)，图象关于原点对称， 偶函数：f-x  =fx  ，图象关于y轴对称 ③奇偶性的运算 第 页 共 页 2 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~ ~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~ ~~~~~ ~ ~ 【典例1】(2023·全国·统考高考真题)若fx ~ ~  =x-1  π 2+ax+sinx+ 2  为偶函数，则a= ． 【典例2】(2023·全国·统考高考真题)若fx  =x+a  2x-1 ln 为偶函数，则a=( )． 2x+1 1 A. -1 B. 0 C. D. 1 2 xex 【典例3】(2023·全国·统考高考真题)已知f(x)= 是偶函数，则a= ( ) eax-1 A. -2 B. -1 C. 1 D. 2 【典例4】(2020·山东·统考高考真题)若定义在R的奇函数f(x)在(-∞,0)单调递减，且f(2)=0，则满足 xf(x-1)≥0的x的取值范围是 ( ) A. [-1,1]∪[3,+∞) B. [-3,-1]∪[0,1] C. [-1,0]∪[1,+∞) D. [-1,0]∪[1,3] 【典例5】(2022·全国·统考高考真题)若fx  1 =lna+ 1-x  +b是奇函数，则a= ，b= ． 技巧3 函数周期性的应用及解题技巧 纵观历年考题，函数周期性是函数及高考的重要考点，要熟悉周期性的定义，若能熟悉周期性的运算， 则可提升解题速度，做到快速求解. 知识在线 ①若fx+a  =fx  ，则fx  的周期为：T=a  ②若fx+a  =fx+b  ，则fx  的周期为：T=a-b  ③若fx+a  =-fx  ，则fx  的周期为：T=2a  (周期扩倍问题) ④若fx+a  1 =± fx  ，则fx  的周期为：T=2a  (周期扩倍问题) 【典例1】(全国·高考真题)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)= 2，则f(1)+f(2)+f(3)+⋯+f(50)= A. -50 B. 0 C. 2 D. 50 【典例2】(2022·全国·统考高考真题)已知函数f(x)的定义域为R，且f(x+y)+f(x-y)=f(x)f(y),f(1) 22 =1，则f(k)= ( ) k=1 A. -3 B. -2 C. 0 D. 1 第 页 共 页 3 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~ ~ 【典例3】(2023·全国·模拟预测)若函数fx ~ ~  的定义域为R，且fx+y  +fx-y  1 = fx 2  fy  ，f1  = 2023 2 3，则 f2k-1 k=1   = ． 技巧4 函数对称性的应用及解题技巧 纵观历年考题，函数对称性是函数及高考的重要考点，要熟悉对称性的定义，若能熟悉对称性的运算， 则可提升解题速度，做到快速求解. 知识在线 轴对称 ①若fx+a  =f-x  ，则fx  a 的对称轴为x= 2 ②若fx+a  =f-x+b  ，则fx  a+b 的对称轴为x= 2 点对称 ①若fx+a  =-f-x  ，则fx  a 的对称中心为 ,0 2  ②若fx+a  +f-x+b  =c，则fx  a+b c 的对称中心为 , 2 2  【典例1】(全国·高考真题)下列函数中，其图像与函数y=lnx的图像关于直线x=1对称的是 ( ) A. y=ln(1-x) B. y=ln(2-x) C. y=ln(1+x) D. y=ln(2+x) x+1 【典例2】(2016·全国·高考真题)已知函数f(x)(x∈R)满足f(-x)=2-f(x)，若函数y= 与y= x m f(x)图像的交点为(x,y),(x ,y ),⋅⋅⋅,(x ,y ),则∑(x +y)= 1 1 2 2 m m i i i=1 A. 0 B. m C. 2m D. 4m 【典例3】(2022·全国·统考高考真题)已知函数f(x),g(x)的定义域均为R，且f(x)+g(2-x)=5,g(x)- 22 f(x-4)=7．若y=g(x)的图像关于直线x=2对称，g(2)=4，则 fk k=1   = ( ) A. -21 B. -22 C. -23 D. -24 【典例4】(2023·湖南·湖南师大附中校联考一模)(多选)已知函数fx  1 =cosx+ ，则 ( ) cos2x A. fx  的图象关于直线x=π轴对称 B. fx  π 的图象关于点 ,0 4  中心对称 C. fx  的所有零点为2k+1  π,k∈Z D. fx  是以π为周期的函数 技巧5 函数4大性质的综合应用及解题技巧 纵观历年考题，函数对称性是函数及高考的重要考点，要熟悉对称性的定义，若能熟悉对称性的运算， 则可提升解题速度，做到快速求解. 知识在线 1.周期性对称性综合问题 ①若fa+x  =fa-x  ，fb+x  =fb-x  ，其中a≠b，则fx  的周期为：T=2a-b  ②若fa+x  =-fa-x  ，fb+x  =-fb-x  ，其中a≠b，则fx  的周期为： 第 页 共 页 4 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ T=2a-b ~ ~ ~ ~  ③若fa+x  =fa-x  ，fb+x  =-fb-x  ，其中a≠b，则fx  的周期为： T=4a-b  2.奇偶性对称性综合问题 ①已知fx  为偶函数，fx+a  为奇函数，则fx  的周期为：T=4a  ②已知fx  为奇函数，fx+a  为偶函数，则fx  的周期为：T=4a  【典例1】(2021·全国·统考高考真题)设函数fx  的定义域为R，fx+1  为奇函数，fx+2  为偶函数， 当x∈1,2  时，f(x)=ax2+b．若f0  +f3  9 =6，则f 2  = ( ) 9 3 7 5 A. - B. - C. D. 4 2 4 2 【典例2】(2023·浙江·统考一模)设函数y=fx  的定义域为R，且fx+1  为偶函数，fx-1  为奇函数， 当x∈-1,1  时，fx  2023 =1-x2，则 fk k=1   = . 技巧6 “奇函数+常函数”的最大值+最小值解题技巧 在模拟考试及高考考试中，会遇到“奇函数+常函数”类型求解，如能掌握相关本质结论和两类指对函 数的奇偶性，则最大值+最小值可秒解。比如在定义域内，若Fx  =fx  +A，其中fx  为奇函数，A为 常数，则最大值M，最小值m有M+m=2A，即M+m=2倍常数 知识在线 (1)与指数函数相关的奇函数和偶函数 f(x)=ax+a-x，(a>0，且a≠1)为偶函数， f(x)=ax-a-x，(a>0，且a≠1)为奇函数 ax-1 ax+1 f(x)= 和f(x)= ，(a>0，且a≠1)为其定义域上的奇函数 ax+1 ax-1 2 2 f(x)=1- 和f(x)=1+ ，(a>0，且a≠1)为其定义域上的奇函数 ax+1 ax-1 f(x)=ax  为偶函数 (2)与对数函数相关的奇函数和偶函数 f(x)=log ( 1+b2x2±bx)，(a>0且a≠1)为奇函数， a b±cx f(x)=log ，(a>0且a≠1)为奇函数 ab∓cx 【典例1】(2023·江苏镇江·高三统考)已知函数 f x  = ax3 - ln x2+1+x  + 3sinx + 7，x ∈ -2023,2023  的最大值为M，最小值为m，则M+m= . 【典例2】(2023·山东统考期中)设函数 fx  2023x+1 =  2+x2025 -3≤x≤3 x2+1  的最大值为M，最小值为 m，则M+m= . 【典例3】(2023·重庆校考)函数fx  x = + 3，当x∈-2023,2023 x2+1  时fx  的最大值为M，最小值 为N，则M+N= ． 第 页 共 页 5 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~ ~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~ ~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~ ~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~ ~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~ ~~~~~~ ~ ~ 【典例4】(2023·安徽·高三校联考)函数fx ~ ~  =x2-6x  sinx-3  +x+a x∈0,6    的最大值为M，最 小值为m，若M+m=8，则a= ． 【典例5】(2023·黑龙江·高三校考)设函数fx  x3+2x+1 =  2+3 在区间-2,2 x2+1  上的最大值为M，最小 值为N，则M+N的值为 ． 【典例6】(2023·黑龙江校考)已知函数fx  =log  1+4x2+2x 2  2ex + ，若fx ex+1  在区间-t,t  t>0  上 的最大值和最小值分别为M，N，则函数gx  =M+N  x+ M+N   x-1  -3的图像的对称中心为 ． 【典例7】(2023·莆田·高三联考)函数fx  =x2-6x  sinx-3  +x+a x∈0,6    的最大值为M，最小 值为m，若M+m=10，则a= ． 技巧7 “奇函数+常函数”的f(a)+f(-a)解题技巧 在模拟考试及高考考试中，会遇到“奇函数+常函数”类型求解，如能掌握相关本质结论和两类指对函 数的奇偶性，则f(a)+f(-a)可秒解.在定义域内，若Fx  =fx  +A，其中fx  为奇函数，A为常数，有 fa  +f-a  =2A，即fa  +f-a  =2倍常数 知识在线 【典例1】(全国·高考真题)已知函数fx  =ln 1+x2-x  +1，fa  =4，则f-a  = ． 【典例2】(2023·四川模拟)已知fx  =x3+sinx+5，若fsinx  =9，则f sinπ+x    . 【典例3】(2023·四川达州·统考一模)函数 fx  x-2 =ln +mtanx+3，且 ft x+2  =6，则 f-t  的值为 . 技巧8 已知函数解析式判断函数图象解题技巧 本题型在高考中以小题形式考查，是高频考题；本题型可以用方法技巧作答，结合奇偶性的判断，特值 的辅助，极限思想的应用可以快速求解，所以几类特值需重点掌握. 知识在线 1.函数的奇偶性 ①具有奇偶性的函数定义域关于原点对称(大前提) ②奇偶性的定义： 奇函数：f-x  =-f(x)，图象关于原点对称， 偶函数：f-x  =fx  ，图象关于y轴对称 ③奇偶性的运算 第 页 共 页 6 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 2.特值与极限 ① 2=1.414,⥄ 3=1.732, 5=2.236, 6=2.45, 7=2.646 1 ②e=2.71828,e2=7.39,e2= e=1.65 1 ③ln1=0,ln2=0.69,ln3=1.1,lne=1,ln e= 2 ④sin1=0.84,cos1=0.54,sin2=0.91,cos2=-0.42 特别地：当x→0时sinx=x 例如：sin0.1=0.099≈0.1，sin0.2=0.199≈0.2,sin0.3=0.296≈0.3 当x→0时cosx=1 cos0.1=0.995≈1,cos(-0.2)=0.980≈1 ~ ~ 【典例1】(2022·全国·统考高考真题)函数y=3x-3-x ~ ~  cosx在区间 - π , π  2 2  的图象大致为 ( ) A． B． C． D． 【典例2】(2022·天津·统考高考真题)函数fx  x2-1 =  的图像为 ( ) x A． B． 第 页 共 页 7 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~ ~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~ C． D． ~ ~ ln|x| 1 【典例3】(2023·辽宁葫芦岛·统考二模)函数 y= + 在-2,0 x2 x2  ∪0,2  上的大致图象为 ( ) A. B. C. D. 【典例4】(2023·山东德州·三模)函数fx  xlnx =  的图象大致是 ( ) ex+e-x A. B. C. D. 【典例5】(2023·全国·模拟预测)函数fx  x3 =sin +x 3  2x ⋅ln  +2 2x  的图像可能是 ( ) A. B. C. D. 【典例6】(2023·湖南益阳·统考模拟预测)函数fx  lne2x+1 =  -x 的部分图象大致是 ( ) x2-1 第 页 共 页 8 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ A. B. C. D. ~ ~ 【典例7】(2023·福建·统考模拟预测)函数fx  lnx =  -x2+2 的图象大数为 ( ) x A. B. C. D. 【典例8】(2023·安徽合肥·合肥一六八中学校考模拟预测)数学与音乐有着紧密的关联.声音中也包含正 弦函数，声音是由于物体的振动产生的能引起听觉的波，每一个音都是由纯音合成的.纯音的数学模型 是函数y=Asinωx，我们平时听到的音乐一般不是纯音，而是有多种波叠加而成的复合音．已知刻画 1 1 某复合音的函数为sinx+ sin2x+ sin3x，则其部分图象大致为 ( ) 2 3 A. 第 页 共 页 9 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ B. C. D. ~ ~ 技巧9 已知函数图象判断函数解析式解题技巧 本题型在高考中以小题形式考查，是高频考题；本题型可以用方法技巧作答，结合奇偶性的判断，特值 的辅助，极限思想的应用可以快速求解，所以几类特值需重点掌握. 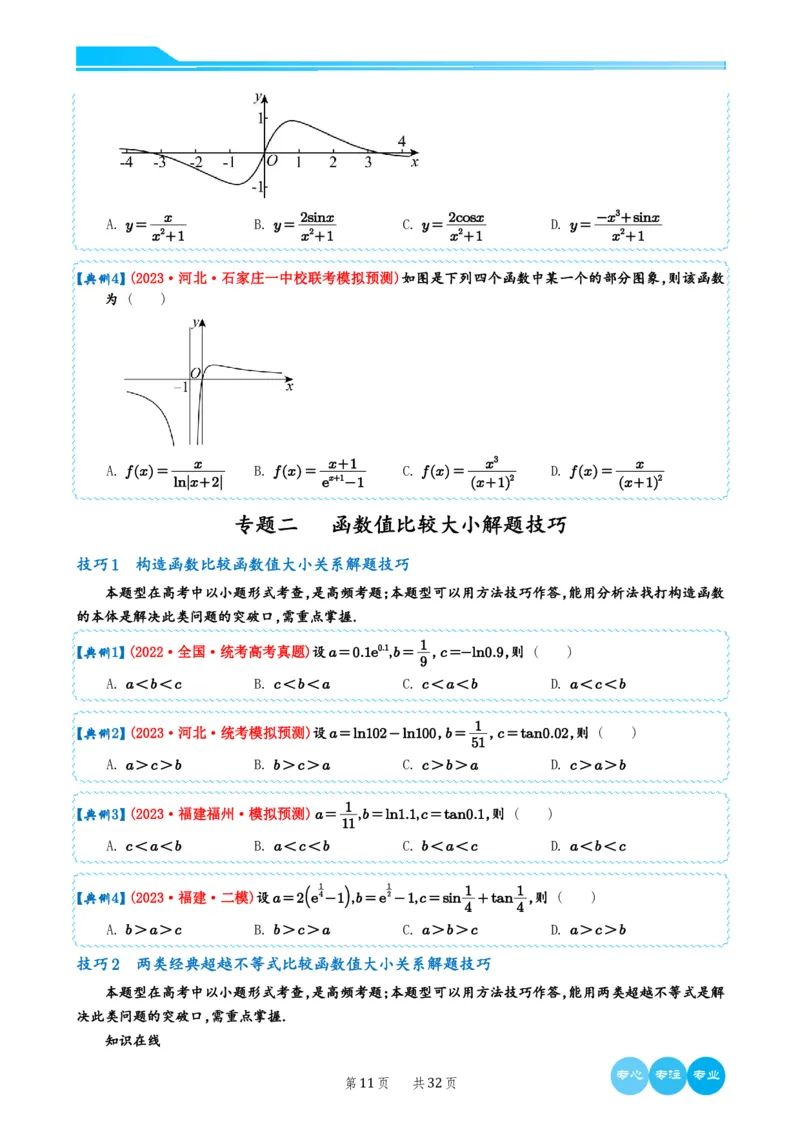【典例1】(2022·全国·统考高考真题)如图是下列四个函数中的某个函数在区间[-3,3]的大致图像，则该 函数是 ( ) -x3+3x x3-x 2xcosx 2sinx A. y= B. y= C. y= D. y= x2+1 x2+1 x2+1 x2+1 【典例2】(2023·天津·统考高考真题)函数fx  的图象如下图所示，则fx  的解析式可能为 ( ) 5ex-e-x A.  5sinx 5ex+e-x B. C. x2+2 x2+1  5cosx D. x2+2 x2+1 【典例3】(2023·浙江温州·统考二模)某个函数的大致图象如图所示，则该函数可能是 ( ) 第 页 共 页 10 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~ x 2sinx 2cosx -x3+sinx A. y= B. y= C. y= D. y= x2+1 x2+1 x2+1 x2+1 ~ ~ 【典例4】(2023·河北·石家庄一中校联考模拟预测)如图是下列四个函数中某一个的部分图象，则该函数 为 ( ) A. fx  x = lnx+2  B. fx  x+1 = C. fx ex+1-1  x3 = x+1  D. fx 2  x = x+1  2 专题二 函数值比较大小解题技巧 技巧1 构造函数比较函数值大小关系解题技巧 本题型在高考中以小题形式考查，是高频考题；本题型可以用方法技巧作答，能用分析法找打构造函数 的本体是解决此类问题的突破口，需重点掌握. 1 【典例1】(2022·全国·统考高考真题)设a=0.1e0.1,b= ，c=-ln0.9，则 ( ) 9 A. ac>b B. b>c>a C. c>b>a D. c>a>b 1 【典例3】(2023·福建福州·模拟预测)a= ,b=ln1.1,c=tan0.1，则 ( ) 11 A. ca>c B. b>c>a C. a>b>c D. a>c>b 技巧2 两类经典超越不等式比较函数值大小关系解题技巧 本题型在高考中以小题形式考查，是高频考题；本题型可以用方法技巧作答，能用两类超越不等式是解 决此类问题的突破口，需重点掌握. 知识在线 第 页 共 页 11 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ 1 x ex≥x+1，ex≥ex，1- ≤lnx≤x-1，lnx≤ x e ~ ~ 【典例1】(2023上·河北保定·高三校联考开学考试)已知a=ln1+e ~ ~  2e ，b= e，c= ，则 ( ) 3 A. b>a>c B. a>c>b C. b>c>a D. 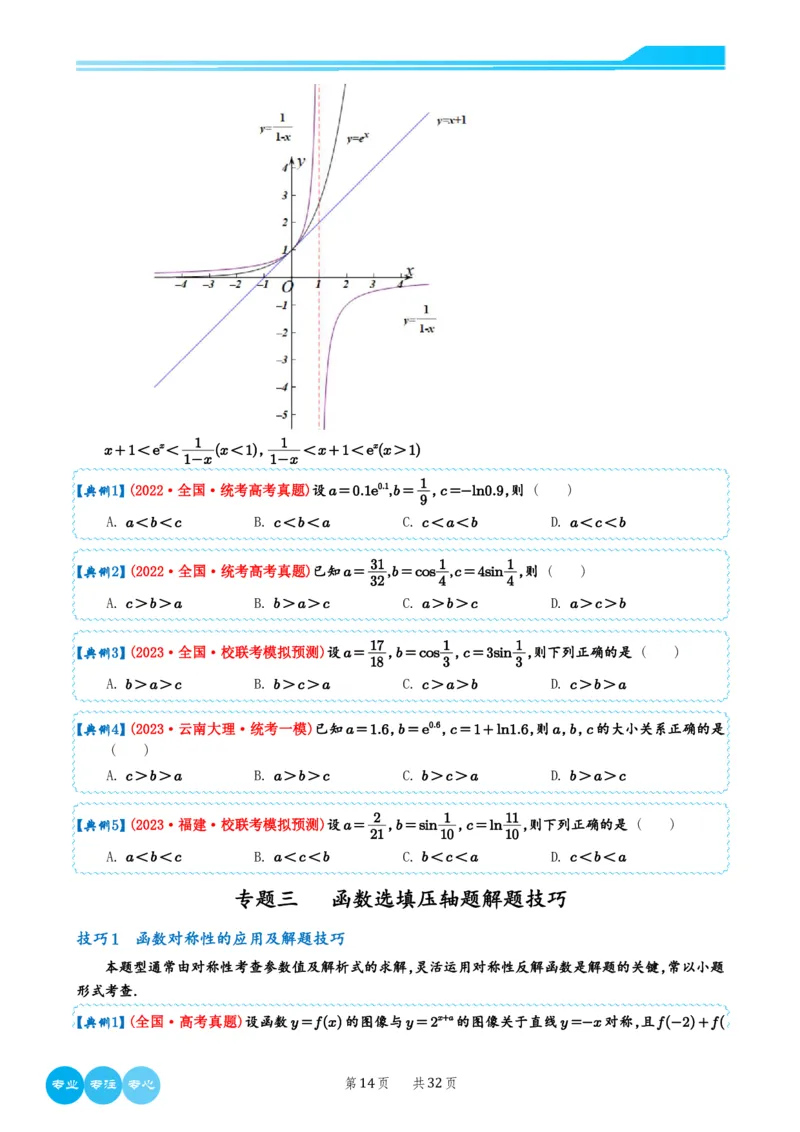c>b>a 1 1 4 【典例2】(2023·河南开封·统考模拟预测)已知a= ，b=e3-1，c=ln ，则 ( ) 3 3 A. a-1)． 结论2 lnx≤x-1    (x>0)． 1 结论3 1- ≤lnx(x>0)． x x 1 x 结论4 -1  ． 结论6 ex≥1+x    (x∈R)； 结论7 e-x≥1-x    (x∈R) 1 结论8 ≥ex x<1 1-x  ． 1 结论9 ≤ex x>1 1-x  ． 1 【典例1】(2022年新Ⅰ卷高考真题第7题)设a=0.1e0.1，b= ，c=-ln0.9则 ( ) 9 A. ab>a B. b>a>c C. a>b>c D. a>c>b 【典例3】(2021·全国·统考高考真题)设a=2ln1.01，b=ln1.02，c= 1.04-1．则 ( ) A. a1)，lnx> x- (01)，lnx> x- 2 x  (0- x2+2x- (x>1)，lnx<- x2+2x- (0 (x>1)，lnx< (02) 第 页 共 页 13 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ 1 1 x+11) 1-x 1-x ~ ~ 1 【典例1】(2022·全国·统考高考真题)设a=0.1e0.1,b= ，c=-ln0.9，则 ( ) 9 A. ab>a B. b>a>c C. a>b>c D. a>c>b 17 1 1 【典例3】(2023·全国·校联考模拟预测)设a= ，b=cos ，c=3sin ，则下列正确的是 ( ) 18 3 3 A. b>a>c B. b>c>a C. c>a>b D. c>b>a 【典例4】(2023·云南大理·统考一模)已知a=1.6，b=e0.6，c=1+ln1.6，则a，b，c的大小关系正确的是 ( ) A. c>b>a B. a>b>c C. b>c>a D. b>a>c 2 1 11 【典例5】(2023·福建·校联考模拟预测)设a= ，b=sin ，c=ln ，则下列正确的是 ( ) 21 10 10 A. af2x-1  成立的x的取值范围 是 1 A.  ,1 3  1 B. -∞, 3  ∪1,+∞  1 1 C. - , 3 3  1 D. -∞,- 3  1 ∪ ,+∞ 3  【典例2】(2023·重庆南开中学校考模拟预测)已知函数 fx  x+1,x∈0,3 2 2 =  2-fx-3 2  ,x∈ 3,+∞ 2    ，则 fx  > log x 2  的解集是 ( ) 1 A.  ,1 2  B. 1,2  1 C.  ,2 2  1 D.  ,1 2  ∪1,2  【典例3】(2024·山东省淄博实验中学校联考模拟预测)已知函数fx  =log 33x-1+3  1 - x，若fa-1 2  ≥ f2a+1  成立，则实数a的取值范围为 ( ) A. -∞,-2  B. -∞,-2  ∪0,+∞  C.  -2, 4  3  D. -∞,-2  ∪  4 ,+∞  3  技巧3 整数解的应用及解题技巧 在整数解问题中，通常我们用猜根法比较快，先找到临界条件得到端点值，再利用整数解区间为一开一 闭，能做到快速求解. 【典例1】(2024·全国·模拟预测)已知关于x的不等式lnx-kx4+kx3>0恰有一个整数解，则实数k的取 值范围为 ( ) 第 页 共 页 15 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~~~~ ~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~ ~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~ ~~~~ A.   ln3 , 1  54 8 ~ ~  B.   ln3 , 1  27 8  ln2 C. -∞, 8  D.   ln3 , ln2  54 8  3a-1 【典例2】(2023·四川内江·统考三模)若关于x的不等式lnx+a- <0有且只有一个整数解，则正 x 实数a的取值范围是 ( ) 1 A.  ,2ln2+1 2  1 B.  ,3ln3+1 2  C. 2ln2+1,3ln3+1  1 D. ln2+ ,3ln3+1 2     【典例3】(2023·全国·模拟预测)已知函数fx  =lnx-ax3-x2  ，若不等式fx  >0有3个整数解，则实 数a的取值范围为 ( ) A.   ln5 , ln2 100 24  B.   ln5 , ln2 125 32  C.   ln3 , ln2  18 4  D.   ln3 , ln2  27 8  1 【典例4】(2023·全国·高三专题练习)已知函数f(x)=lnx- x2+1，若f(x)-kx>0恰有3个正整数 2 解，则k的取值范围为 ( ) A.   ln2 - 7 , ln3 - 7  2 4 3 6  ln2 7 ln3 7 B.  - , - 2 4 3 6  ln2 7 ln3 7 C.  - , - 2 4 3 6  D.   ln2 - 7 , ln3 - 7  2 4 3 6  【典例5】(2022·哈尔滨·哈九中校考二模)偶函数fx  满足f4+x  =f4-x  ，当x∈0,4  时，fx  = lnx ，不等式 f2 x x  +afx  >0在 -200,200  上有且只有100个整数解，则实数a的取值范围是 ( ) 1 1 A. - ln3, ln2 3 2  B.  - 1 ln3,- 1 ln2  3 2  1 1 C. - ln3,- ln2 3 2  1 1 D. - ln3, ln2 3 2  技巧4 零点的应用及解题技巧 零点问题是高考中常考内容，解决唯一零点问题在于观察发现零点的具体值，多个零点数形结合能做 到快速求解. 【典例1】(全国·高考真题)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点，则a= 1 1 1 A. - B. C. D. 1 2 3 2 【典例2】(2023·山东济南·统考三模)已知函数fx  (x+1)2,x≤0, = lgx    若函数gx ,x>0,  =fx  -b有四个不 同的零点，则实数b的取值范围为 ( ) A. 0,1  B. 0,1  C. 0,1  D. 1,+∞  【典例3】(2023·安徽蚌埠·统考模拟预测)已知函数fx  =x2-ln1+x  -lna-x  有唯一零点，则a= ( ) 1 A. 0 B. - C. 1 D. 2 2 第 页 共 页 16 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~ ~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~ ~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~ ~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~ ~ 【典例4】(2022·云南曲靖·高三曲靖一中校考阶段练习)已知函数fx ~ ~  =m2 x- 2 1 +2 -x+ 2 1  +x2-x有唯一 零点，则m的值为 ( ) 1 1 1 1 A. - B. C. D. 2 3 2 8 【典例5】(2023·湖南岳阳·统考二模)若函数fx  =ex2-2lnx-2alnx+ax2有两个不同的零点，则实数a的 取值范围是 ( ) A. -∞,-e  B. -∞,-e  C. -e,0  D. - e,0  ex，x≤0， 【典例6】(全国·高考真题)已知函数f(x)= g(x)=f(x)+x+a．若g(x)存在2个零点，则a的 lnx，x>0， 取值范围是 A. [-1，0) B. [0，+∞) C. [-1，+∞) D. [1，+∞) 【典例7】(2023·贵州贵阳·校联考三模)已知函数fx  cosπx-πa =  , x0时，f(x)<-1，求a的取值范围； 第 页 共 页 18 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~ ~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~ ~~~~ 1 1 1 (3)设n∈N∗，证明： + +⋯+ >ln(n+1)． 12+1 22+2 n2+n ~ ~ 技巧2 函数凹凸性解题技巧 函数凹凸性是函数的一种特殊特征,近年来,以函数凹凸性为背景的题目屡见不鲜,这些试题情景新 颖,能考查学生的创新能力和潜在的数学素质,常作为压轴题出现.虽然在高中课本中没有这方面的内容, 但高中教师若能多了解一些函数凹凸性的相关理论知识,可以“登高望远”,便于找到问题的本质内涵,确 定解题方向,寻找简捷的解题途径. 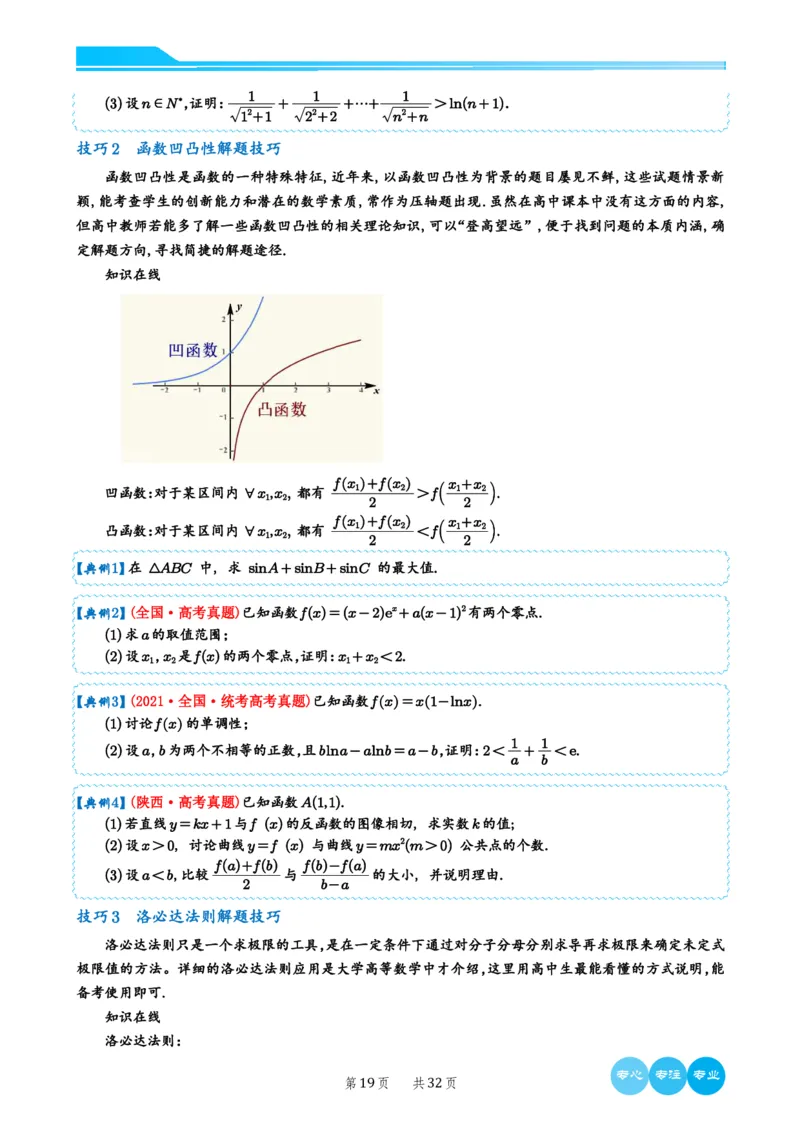知识在线 凹函数：对于某区间内 ∀x,x , 都有 fx 1 1 2  +fx 2  x +x >f 1 2 2 2  . 凸函数：对于某区间内 ∀x,x , 都有 fx 1 1 2  +fx 2  x +x 0, 讨论曲线y=f (x) 与曲线y=mx2(m>0) 公共点的个数. f(a)+f(b) f(b)-f(a) (3)设a + 恒成立, 求 k 的取值范围. x+1 x x-1 x 【典例2】(全国高考)∀x∈(0,+∞),ex-1-x-ax2≥0 恒成立, 求 a 的取值范围 【典例3】(天津高考)∀x∈[0,+∞),x-ln(x+1)≤ax2 恒成立, 求a的取值范围. 【典例4】(2023·江苏模拟)已知函数fx  =1+x  e-2x,gx  x3 =ax+ +1+2xcosx.当x∈0,1 2  时， (I)求证1-x≤fx  1 ≤ ; 1+x (II)若fx  ≥gx  恒成立，求实数a的取值范围. 专题五 不等式相关解题技巧 技巧1 基本不等式链的应用及解题技巧 本题型通常考查基本不等式及其基本不等式链的应用，掌握基本不等式链，可以较快速解决代数式的 大小比较及其相关最值求解，常以小题形式考查. 知识在线 第 页 共 页 20 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~ ~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~ ~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ a2+b2 a+b 2 基本不等式链: ≥ ≥ ab≥ (a>0,b>0), 2 2 1+1 a b 当且仅当 a=b 时, 等号成立. a2+b2 a+b 2 其中 , , ab, 分别为 a,b 平方平均数, 算术平均数, 几何平均数, 调和平均数.可 2 2 1+1 a b 利用上述不等式链在各平均数间进行放缩、转化. ~ ~ 【典例1】(2022·全国·统考高考真题)若x，y满足x2+y2-xy=1，则 ( ) A. x+y≤1 B. x+y≥-2 C. x2+y2≤2 D. x2+y2≥1 ~ ~ 【典例2】(2023·湖北·模拟预测)(多选)若a>0，b>0，a+b=2，则下列不等式中对一切满足条件的a， b恒成立的有 ( ) 2 1 A. ab≤1 B. a+b≤2 C. a2+b2≥2 D. + ≥3 2 a b 【典例3】(2023·广东汕头·金山中学校考三模)(多选)若a>0,b>0,a+b=4，则下列不等式对一切满足 条件a,b恒成立的是 ( ) a2 1 1 A. ab≤2 B. a+ b≤2 C. +b2≥4 D. + ≥1 3 a b 【典例4】(2023·江苏模拟)(多选)已知实数x，y满足3x2+3y2-2xy=5，则 ( ) 5 y 15 A. xy≤1 B. x+y≥- 5 C. x2+y2≥ D. x- ≥- 4 3 3 技巧2 权方和不等式的应用及解题技巧 在条件等式求最值或“1”的妙用求最值中，我们通常使用基本不等式(链)来求最值，解题中往往会遇到 思路繁琐，计算量大的情况，学生不易求解，而此时的权方和不等式优势极其明显，可以做到快速求解，常在 小题中使用. 知识在线 权方和不等式的初级应用: a2 b2 (a+b)2 a b 若 a,b,x,y>0 则 + ≥ 当且仅当 = 时取等. x y x+y x y (注：熟练掌握权方和不等式的初级应用，足以解决高考中的这类型最值问题的秒杀) 1 1 1 【典例1】(2023·浙江模拟)已知a>1,b> ，且2a+b=3，则 + 的最小值为 ( ) 2 a-1 2b-1 9 1 A. 1 B. C. 9 D. 2 2 1 1 【典例2】(2023·四川·校联考一模)已知正数x，y满足x+y=5，则 + 的最小值是 . x+2 y+2 2 1 【典例3】(2023·辽宁鞍山·鞍山一中校考二模)设a>0,b>2且a+b=4，则 + 的最小值是 a b-2 ． 第 页 共 页 21 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~ ~ x2 【典例4】(2023·黑龙江佳木斯·佳木斯一中校考模拟预测)已知正数x，y满足x+y=4，若a≤ + x+1 y2 恒成立，则实数a的取值范围是 ． y+2 ~ ~ 技巧3 普通型糖水不等式的应用及解题技巧 在应用不等式的性质进行代数式大小比较时，我们除了常规的不等式性质，特值，还可以学习糖水不等 式及其倒数形式，常在小题中使用，能做到快速求解. 知识在线 1.糖水不等式定理: b+m b 若 a>b>0,m>0, 则一定有 > a+m a 通俗的理解: 就是 a 克的不饱和糖水里含有 b 克糖, 往糖水里面加入 m 克糖,则糖水更甜; 2. 糖水不等式的倒数形式: a a+m 设 a>b>0,m>0, 则有: > b b+m 【典例1】(2023·湖南长沙·长郡中学校考二模)已知实数a,b,c满足0 B. > c-a b-a a a+c 1 C. ac-a  1 > bc-a  D. ab+c2>ac+bc 【典例2】(2020·全国·统考高考真题)已知55<84，134<85．设a=log 3，b=log 5，c=log 8，则 5 8 13 ( ) A. a0，b>0，且a>b)，若再添 加c克糖c>0  b+c b 后，(假设全部溶于水)，糖水会更甜，于是得出一个不等式： > ，称之为“糖水 a+c a 不等式”，则下列命题一定正确的是 ( ) b+m b A. 若a>b>0，m>0，则 与 大小关系不随m的变化而变化 a+m a b b+m B. 若a>b>0，-bb>0，c>d>0，则 < a+d a+c a+b a b D. 若a>0，b>0，则 < + 1+a+b 1+a 1+b 技巧4 对数型糖水不等式的应用及解题技巧 在应用不等式的性质进行代数式大小比较时，我们除了常规的不等式性质，特值，还可以学习对数型糖 水不等式及其倒数形式，常在小题中使用，能做到快速求解. 知识在线 (1) 设 n∈N , 且 n>1, 则有 log nb>1,m>0, 则有 log bb>1,m>0, 则有 loga>log (a+m) b b+m 第 页 共 页 22 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ ~ ~ 【典例1】(2022·全国·统考高考真题)已知9m=10,a=10m-11,b=8m-9，则 ( ) A. a>0>b B. a>b>0 C. b>a>0 D. b>0>a ~ ~ 【典例2】(2022·安徽黄山·统考一模)下列不等式不正确的是 ( ) A． 7- 5< 6-2B．π3.1<3.1π 1 1 B．C．5sin >cos D．log 31，则D与A位于BC两侧 x+y=1时，当x>0,y>0，则D在线段BC上；当xy<0，则D在线段BC 延 长线上 (2)已知D在线段BC上，且BD ~ ~ ~ ~  :CD    n =m:n，则AD= AB+ m+n  m AC m+n   【典例1】(全国·高考真题)设D为△ABC所在平面内一点，且BC=3CD，则 ( )       1 4 1 4 A. AD=- AB+ AC B. AD= AB- AC 3 3 3 3       4 1 4 1 C. AD= AB+ AC D. AD= AB- AC 3 3 3 3      1 2 【典例2】(2023江苏模拟)如图，在△ABC中，AN = NC，P是BN上的一点，若AP=mAB+ AC，则 3 11 实数m的值为 ( ) 9 5 3 2 A. B. C. D. 11 11 11 11     【典例3】(2022·全国·统考高考真题)在△ABC中，点D在边AB上，BD=2DA．记CA=m，CD=n，  则CB= ( )         A. 3m-2n B. -2m+3n C. 3m+2n D. 2m+3n 【典例4】(2020·新高考全国1卷·统考高考真题)已知平行四边形ABCD，点E，F分别是AB，BC的中点      (如图所示)，设AB=a，AD=b，则EF等于 ( ) 1   A. a+b 2  1   B. a-b 2  1   C. b-a 2  1   D. a+b 2  【典例5】(全国·高考真题)在△ABC中，AD为BC边上的中线，E为AD的中点，则EB=         3 1 1 3 3 1 1 3 A. AB- AC B. AB- AC C. AB+ AC D. AB+ AC 4 4 4 4 4 4 4 4 第 页 共 页 26 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~ ~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~ ~ 1 2 【典例6】(江苏·高考真题)设D、E分别是ΔABC的边AB，BC上的点，AD= AB，BE= BC. 若DE 2 3   =λAB+λ AC(λ,λ 为实数)，则λ +λ 的值是 ~ 1 2 1 2 1 2 ~ 技巧2 系数和(等和线)的应用及解题技巧 近年，高考、模考中有关“系数和(等和线)定理”背景的试题层出不穷，学生在解决此类问题时，往往要 通过建系或利用角度与数量积处理，结果因思路不清、解题繁琐，导致得分率不高，而向量三点共线定理与 等和线巧妙地将代数问题转化为图形关系问题，将系数和的代数运算转化为距离的比例运算，数形结合思 想得到了有效体现，同时也为相关问题的解决提供了新的思路，大家可以学以致用 知识在线 如图，P为ΔAOB所在平面上一点，过O作直线l⎳AB，由平面向量基本定理知：    存在x,y∈R，使得OP=xOA+yOB 下面根据点P的位置分几种情况来考虑系数和x+y的值   ①若P∈l时，则射线OP与l无交点，由l⎳AB知，存在实数λ，使得OP=λAB       而AB=OB-OA，所以OP=λOB-λOA，于是x+y=λ-λ=0 ②若P∉l时， (i)如图1，当P在l右侧时，过P作CD⎳AB，交射线OA，OB于C,D两点，则 ΔOCD∼ΔOAB，不妨设ΔOCD与ΔOAB的相似比为k 由P,C，D三点共线可知：存在λ∈R使得：      OP=λOC+(1-λ)OD=kλOA+k(1-λ)OB 所以x+y=kλ+k(1-λ)=k (ii)当P在l左侧时，射线OP的反向延长线与AB有交点，如图1作P关于O的对称点P，由(i)的分 析知：存在存在λ∈R使得：      OP=λOC+(1-λ)OD=kλOA+(1-λ)OB    所以OP=-kλOA+-(1-λ)OB 于是x+y=-kλ+-k(1-λ)=-k    综合上面的讨论可知：图中OP用OA,OB线性表示时，其系数和x+y只与两三角形的相似比有关。 我们知道相似比可以通过对应高线、中线、角平分线、截线、外接圆半径、内切圆半径之比来刻画。因为 三角形的高线相对比较容易把握，我们不妨用高线来刻画相似比，在图中，过O作AB边的垂线l，设点P |OP| 在l上的射影为P，直线l交直线AB于点P，则|k|= (k的符号由点P的位置确定)，因此只需求出 1 |OP| 1 |OP|的范围便知x+y的范围 【典例1】(全国·高考真题)在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆    上．若AP=λ AB+μAD，则λ+μ的最大值为 第 页 共 页 27 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~ ~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~ ~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ A. 3 B. 2 2 C. 5 D. 2 ~ ~ 【典例2】(衡水中学二模)边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD(含短点)上    运动，P是圆Q上及其内部的动点，设向量AP=mAB+nAF(m,n∈R)，则m+n的取值范围是 ( ) A. 1,2  B. 5,6  C. 2,5  D. 3,5     【典例3】已知△ABC为边长为2的等边三角形，动点P在以BC为直径的半圆上.若AP=λAB+μAC，则 2λ+μ的取值范围是   【典例4】在矩形ABCD中，AB=1,AD=2，动点P在以点C为圆心且与BD相切的圆上，若AP=λAB+  μAD，则λ+μ的最大值为 ( ) A3 B2 2 C 5 D2 【典例5】如图，正六边形ABCDEF，P是ΔCDE内(包括边界)的动    点，设AP=αAB+βAF(α,β∈R)，则α+β的取值范围是 【典例6】如图在直角梯形ABCD中，AB⎳CD，AB⊥AD，AD=DC=1，AB=3，动点P在以C为圆心，    且与直线BD相切的圆内运动，设AP=αAD+βAB(α,β∈R) 则α+β的取值范围是     【典例7】若点C在以P为圆心,6为半径的弧AB上,且PC=xPA+yPB,则2x+3y的取值范围为 【典例8】(2023·浙江·高三专题练习)如图，在直角梯形ABCD中，AB⊥AD，AB∥DC，AB=2，AD  1 =DC=1，图中圆弧所在圆的圆心为点C，半径为 ，且点P在图中阴影部分(包括边界)运动．若AP 2   =xAB+yAC，其中x，y∈R，则4x-y的取值范围是 ( ) A.  2，  3+ 3 2  4  B.  2，  3+ 5  2  C.  3- 2 ，  3+ 5  4 2  D.  3- 17 ，  3+ 17  2 2  技巧3 极化恒等式的应用及解题技巧 第 页 共 页 28 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~ ~~~~~~~ 利用向量的极化恒等式可以快速对共起点(终点)的两向量的数量积问题数量积进行转化，体现了向量 的几何属性，让“秒杀”向量数量积问题成为一种可能，此恒等式的精妙之处在于建立了向量的数量积与几 何长度(数量)之间的桥梁，实现向量与几何、代数的巧妙结合，对于不共起点和不共终点的问题可通过平移 转化法等价转化为对共起点(终点)的两向量的数量积问题，从而用极化恒等式解决，需大家强化学习。 知识在线       (a+b)2-(a-b)2 极化恒等式a⋅b= 4 恒等式右边有很直观的几何意义: 向量的数量积可以表示为以这两个向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的 1 ，恒等式的作用在于向量的线性运算与数量积之间的联系 4     如图在平行四边形 ABCD 中, AB=a,AD=b       (AB+AD)2-(AB-AD)2 则 a⋅b= 4 在上述图形中设平行四边形 ABCD 对角线交于 M 点, 则对于三角形来说:        (AB+AD)2-(AB-AD)2  |DB|2 a⋅b= =|AM|2- 4 4 ~   ~ 【典例1】(2023·全国·统考高考真题)正方形ABCD的边长是2，E是AB的中点，则EC⋅ED= ( ) A. 5 B. 3 C. 2 5 D. 5 ~ ~   【典例2】(江苏·高考真题)如图，在ΔABC中，D是BC的中点，E,F是A,D上的两个三等分点，BA⋅CA     =4，BF⋅CF=-1 ，则BE⋅CE 的值是 . 【典例3】(2022·北京·统考高考真题)在△ABC中，AC=3,BC=4,∠C=90°．P为△ABC所在平面内   的动点，且PC=1，则PA⋅PB的取值范围是 ( ) A. [-5,3] B. [-3,5] C. [-6,4] D. [-4,6] 技巧4 奔驰定理与三角形四心的应用及解题技巧 平面向量问题是高中数学中的一个热点，在高考中考查比重不会很大，一般以选择填空形式出现，难度 一般也会控制在中等，有时也会以压轴题命题。平面向量中有很多重要的应用，比如系数和(等和线)、极化 恒等式、本技法我们继续学习另一个重要的结论-奔驰定理。它将三角形的四心与向量完美地融合到一 第 页 共 页 29 32起，高中的同学们可以将这个内容当成课外拓展知识，同时也是加强对三角形的认识，加深对数学的理解。 奔驰定理”揭示的是平面向量与三角形面积之间所蕴含的一个优美规律并因其图形与奔驰的logo相 似而得名“奔驰定理”，会提升解题效率，可强化学习。 知识在线 2.1.奔驰定理     如图，已知P为△ABC内一点，则有S ⋅OA+S ⋅OB+S ⋅OC=0. △PBC △PAC △PAB 由于这个定理对应的图象和奔驰车的标志很相似，我们把它称为“奔驰定理”. 2.2.奔驰定理的证明 如图：延长OA与BC边相交于点D BD S S S -S S 则 = △ABD = △BOD = △ABD △BOD = △AOB DC S S S -S S △ACD △COD ACD △COD △AOC    DC BD OD= OB+ OC BC BC S  S  = △AOC OB+ △AOB OC S +S S +S △AOC △AOB △AOC △AOB OD S S S +S S ∵ = BOD = COD = BOD COD = △BOC OA S S S +S S +S BOA COA BOA COA △AOC △AOB  S  ∴ OD=- △BOC OA S +S △AOC △AOB S  S  S  ∴- △BOC OA= △AOC OB+ △AOB OC S +S S +S S +S △AOC △AOB △AOC △AOB △AOC △AOB     ∴S ⋅OA+S ⋅OB+S ⋅OC=0 △BOC △AOC △AOB 2.3.奔驰定理的推论及四心问题     推论O是△ABC内的一点,且x⋅OA+y⋅OB+z⋅OC=0,则S :S :S =x:y:z △BOC △COA △AOB 有此定理可得三角形四心向量式 (1)三角形的重心：三角形三条中线的交点叫做三角形的重心，重心到顶点的距离与重心到对边中点的 距离之比为2：1. (2)三角形的垂心：三角形三边上的高的交点叫做三角形的垂心，垂心和顶点的连线与对边垂直. (3)三角形的内心：三角形三条内角平分线的交点叫做三角形的内心，也就是内切圆的圆心，三角形的 内心到三边的距离相等，都等于内切圆半径r. (4)三角形的外心：三角形三条边的垂直平分线的交点叫做三角形的外心，也就是三角形外接圆的圆 心，它到三角形三个顶点的距离相等. 奔驰定理对于利用平面向量解决平面几何问题，尤其是解决跟三角形的面积和“四心”相关的问题，有 专业 专注 专心 第 页 共 页 30 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专心 专注 专业 ~~~~~~~~~ ~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~ 着决定性的基石作用. 已知点O在△ABC内部，有以下四个推论：     ①若O为△ABC的重心，则OA+OB+OC=0；      ②若O为△ABC的外心，则sin2A⋅OA+sin2B⋅OB+sin2C⋅OC=0；或 OA= ~ ~ ~ ~   OB=    OC       ③若O为△ABC的内心，则a⋅OA+b⋅OB+c⋅OC=0；备注：若O为△ABC的内心，则sinA⋅OA+    sinB⋅OB+sinC⋅OC=0也对.          ④若O为△ABC的垂心，则tanA⋅OA+tanB⋅OB+tanC⋅OC=0，或OA⋅OB=OB⋅OC=OC⋅  OA  【典例1】(宁夏·高考真题)已知O，N，P在ΔABC所在平面内，且OA   =OB   =OC     ,NA+NB+NC=       0，且PA•PB=PB•PC=PC•PA，则点O，N，P依次是ΔABC的 (注：三角形的三条高线交于一点，此点为三角型的垂心) A. 重心外心垂心 B. 重心外心内心 C. 外心重心垂心 D. 外心重心内心   【典例2】(江苏·高考真题)O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足OP=OA   AB AC +λ  +  |AB| |AC|  ，λ∈[0,+∞)，则P的轨迹一定通过△ABC的 ( ) A. 外心 B. 内心 C. 重心 D. 垂心    【典例3】(2023春·上海长宁·高三上海市延安中学校考期末)若O是△ABC内一点，OA+OB+OC =  0，则O是△ABC的 ( ) A. 内心 B. 外心 C. 垂心 D. 重心 【典例4】(2023·全国·高三专题练习)奔驰定理：已知点O是△ABC内的一点，若△BOC,△AOC,△AOB     的面积分别记为S,S ,S ，则S ⋅OA+S ⋅OB+S ⋅OC=0．“奔驰定理”是平面向量中一个非常优美 1 2 3 1 2 3 的结论，因为这个定理对应的图形与“奔驰”轿车的logo很相似，故形象地称其为“奔驰定理”．如图，     已知O是△ABC的垂心，且OA+2OB+3OC=0，则cosC= ( ) 3 10 10 2 5 5 A. B. C. D. 10 10 5 5 【典例5】(2023春·湖南株洲·高三炎陵县第一中学校联考期末)(多选)如图.P为△ABC内任意一点，角     A,B,C的对边分别为a,b,c，总有优美等式S PA+S PB+S PC=0成立，因该图形酯似奔 △PBC △PAC △PAB 驰汽车车标，故又称为奔驰定理.则以下命题是真命题的有 ( ) 第 页 共 页 31 32~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 专业 专注 专心 ~~~~~~~~~~~ ~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~ ~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~     A. 若P是△ABC的重心，则有PA+PB+PC=0     B. 若aPA+bPB+cPC=0成立，则P是△ABC的内心    2 1 C. 若AP= AB+ AC，则S :S =2:5 5 5 △ABP △ABC    π D. 若P是△ABC的外心，A= ，PA=mPB+nPC，则m+n∈- 2,1 4 ~ ~   【典例6】(四川·高考真题)在平面内，定点A，B，C，D满足DA   =DB   =DC      ,DA⋅DB=DB⋅DC =    DC⋅DA=-2，动点P，M满足AP     =1，PM =MC，则BM  2的最大值是 43 49 37+6 3 37+2 33 A. B. C. D. 4 4 4 4     【典例7】(2023·全国·高三专题练习)若平面向量a，b，c满足c          =1，a⋅c=1，b⋅c=3，a⋅b=2，则a，b 夹角的取值范围是 ( ) A.   π , π  6 2  B.   π ,π  6  C.   π , π  3 2  D.   π ,π  3          【典例8】(湖南·高考真题)已知a,b是单位向量，a∙b=0.若向量c满足c-a-b   =1,则c  的取值范围是 ( ) A.  2-1，, 2+1  B.  2-1，, 2+2  C. 1，, 2+1  D. 1，, 2+2  【典例9】(湖南·高考真题)已知点A,B,C在圆x2+y2=1上运动，且AB⊥BC，若点P的坐标为(2，0)，则    PA+PB+PC  的最大值为 A. 6 B. 7 C. 8 D. 9         【典例10】(2023·全国·高三专题练习)已知平面向量a=OA，b=OB，c=OC，满足4OC ⋅AC =1-  OA     2，4OB⋅CB=1-OC      2，则向量a-4b与c-2b所成夹角的最大值是 ( ) π π 2π 5π A. B. C. D. 6 3 3 6     【典例11】(2022·浙江湖州·湖州市菱湖中学校考模拟预测)已知平面向量a，b，c满足a   =1，b   =2，a2        =a⋅b，2c2=b⋅c，则c-a  2   +c-b  2的最小值为 . 【典例12】(2023·四川成都·四川省成都市玉林中学校考模拟预测)在平面内，定点A,B,C,O，满足  OA=   OB=    OC       =2，且OA+OB+OC=0，则AB   = ；平面内的动点P,M满足AP  =1，    PM =MC，则|BM|2的最大值是 ． 第 页 共 页 32 32