文档内容
年普通高等学校招生全国统一考试 模拟
2024 ( )
数学试题参考答案及评分标准
2024.3
说明:
一 本解答只给出了一种解法供参考 如考生的解法与本解答不同 可根据试题的主要
、 , ,
考查内容参照评分标准酌情赋分
.
二 当考生的解答在某一步出错误时 如果后继部分的解答未改该题的内容与难度 可
、 , ,
视影响的程度决定后继部分的给分 但不得超过该部分正确答案应得分数一半 如
, ;
果后继部分的解答有较严重的错误或又出现错误 就不再给分
, .
三 解答右端所注分数 表示考生正确做到这一步应得的累加分数
、 , .
四 只给整数分数 选择题和填空题不给中间分
、 , .
一、选择题:本题共 小题,每小题 分,共 分。 在每小题给出的四个选项中,只有一项
8 5 40
是符合题目要求的。
1.B 2.A 3.C 4.C 5.A 6.B 7.D 8.B
二、选择题:本题共 小题,每小题 分,共 分。 在每小题给出的选项中,有多项符合题
3 6 18
目要求。 全部选对的得 分,部分选对的得部分分,有选错的得 分。
6 0
9.ACD 10.BCD 11.AC
三、填空题:本题共 小题,每小题 分,共 分。
3 5 15
12.[1,10) 13. 2 14.36(2+ 3)π 144π
四、解答题:本题共 小题,共 分。 解答应写出文字说明、证明过程或演算步骤。
5 77
. 分
15 (13 )
解 f x a b
:(1) ( )= ·
2x x x 分
=2cos +2 3sin cos ………………………………………………… 1
x x 分
=cos2 +1+ 3sin2 …………………………………………………… 3
x π 分
=2sin(2 + )+1, ……………………………………………………… 4
6
因为f x 11 即 x π 11 所以 x π 3 分
( 0)= , 2sin(2 0+ )+1= , sin(2 0+ )= ,………………… 5
5 6 5 6 5
又x π π 所以 x π π 5π
0∈( , ), 2 0+ ∈( , ),
6 3 6 2 6
所以 x π 4 分
cos(2 0+ )= - , …………………………………………………………… 6
6 5
所以 x x π π 分
cos2 0=cos(2 0+ - ) ……………………………………………………… 7
6 6
数学试题答案 第 页 共 页
1 ( 6 )
{#{QQABAYQQggiAABJAAAhCQw0YCEEQkAAAAIoORBAIsAABCANABAA=}#}x π π x π π
=cos(2 0+ )cos +sin(2 0+ )sin
6 6 6 6
3-4 3. 分
= ………………………………………………………………… 8
10
由题意知 g x 1 x π π x π 分
(2) , ( )= (2sin(2( - )+ )+1-1)=sin(2 - ),……………… 10
2 6 6 6
由g x 1 得 π k x π 5π k k Z
( )≥ , +2 π≤2 - ≤ +2 π, ∈ ,
2 6 6 6
π k x π k k Z 分
∴ + π≤ ≤ + π, ∈ , ……………………………………………………… 11
6 2
令k 得x π π 令k 得x 5π π
=0, ∈[ , ], =-1, ∈[- ,- ],
6 2 6 2
又x π π x π π .
∈[- , ],∴ ∈[ , ]
6 3 6 3
故不等式g x 1 x π π 的解集为 π π . 分
( )≥ , ∈[- , ] [ , ] …………………………… 13
2 6 3 6 3
. 分
16 (15 )
解 随机变量X可能取值为 . 分
(1) : 6,7,8,9 …………………………………………… 1
由题意得每次掷骰子上两级台阶的概率为2 上三级台阶的概率为1 分
, , ………… 2
3 3
则X B 1 分
-6 (3, ) …………………………………………………………………… 3
3
可得P X 2 3 8 分
( =6)=( ) = , ………………………………………………………… 4
3 27
P X C1 1 2 2 4 分
( =7)= 3× ×( ) = , ………………………………………………… 5
3 3 9
P X C2 1 2 2 2 分
( =8)= 3×( ) × = , ………………………………………………… 6
3 3 9
P X 1 3 1 分
( =9)=( ) = , ………………………………………………………… 7
3 27
所以X的分布列为
X
6 7 8 9
P 8 4 2 1
27 9 9 27
因为E X 1 所以E X . 分
( -6)= 3× =1, ( )= 7 …………………………………………… 9
3
数学试题答案 第 页 共 页
2 ( 6 )
{#{QQABAYQQggiAABJAAAhCQw0YCEEQkAAAAIoORBAIsAABCANABAA=}#}解 记甲 乙两位学生参加游戏 恰有一人获得奖品的概率为P
(2) : 、 , ,
由题意知 位于第 级台阶则认定游戏失败 无法获得奖品 所以投掷 次后 学员站
, 10 , , 3 ,
在第 步台阶 第四次投掷次骰子 出现 的倍数 即位于第 级台阶 分
7 , , 3 , 10 , …………… 10
其概率P C1 1 2 2 1 4 分
1= 3× ×( ) × = ,………………………………………………… 12
3 3 3 27
所以P C1 P P 4 23 184. 分
= 2× 1×(1- 1)= 2× × = ………………………………………… 14
27 27 729
甲 乙两位学生参加游戏 恰有一人获得奖品的概率为184. 分
、 , ……………………… 15
729
. 分
17 (15 )
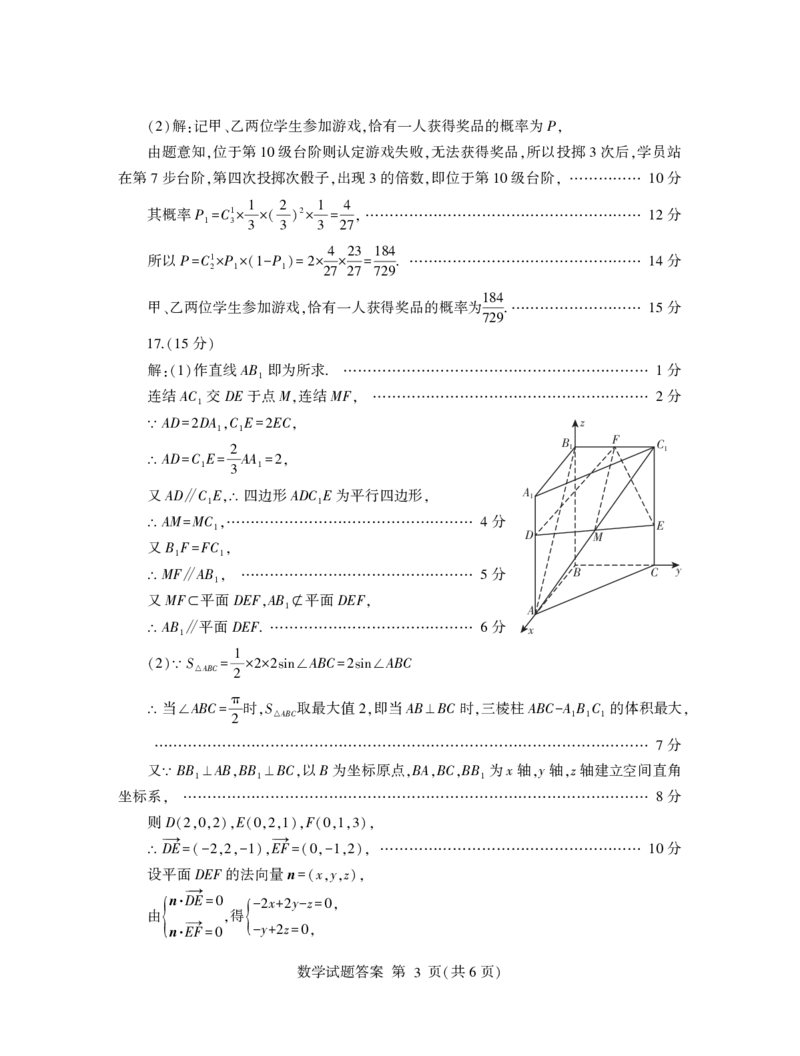
解 作直线AB 即为所求. 分
:(1) 1 ……………………………………………………… 1
连结AC 交DE于点M 连结MF 分
1 , , ………………………………………………… 2
AD DA C E EC [
∵ =2 1, 1 =2 , # ' $
AD C E 2AA
∴ = 1 = 1=2,
3
又AD C E 四边形ADC E为平行四边形 "
∥ 1 ,∴ 1 ,
AM MC 分 &
∴ = 1,…………………………………………… 4 % .
又B F FC
1 = 1,
MF AB 分 # $ Z
∴ ∥ 1, ………………………………………… 5
又MF 平面DEF AB 平面DEF
⊂ , 1⊄ , "
AB 平面DEF. 分 Y
∴ 1∥ …………………………………… 6
S 1 ABC ABC
(2)∵ △ ABC= ×2×2sin∠ =2sin∠
2
当 ABC π时 S 取最大值 即当AB BC时 三棱柱ABC A B C 的体积最大
∴ ∠ = , △ ABC 2, ⊥ , - 1 1 1 ,
2
分
………………………………………………………………………………………… 7
又 BB AB BB BC 以B为坐标原点 BA BC BB 为x轴 y轴 z轴建立空间直角
∵ 1⊥ , 1⊥ , , , , 1 , ,
坐标系 分
, …………………………………………………………………………………… 8
则D E F
(2,0,2), (0,2,1), (0,1,3),
D→E E→F 分
∴ =(-2,2,-1), =(0,-1,2), ……………………………………………… 10
设平面DEF的法向量n x y z
=( , , ),
{n D→E { x y z
由 · =0 得 -2 +2 - =0,
n E→F , y z
· =0 - +2 =0,
数学试题答案 第 页 共 页
3 ( 6 )
{#{QQABAYQQggiAABJAAAhCQw0YCEEQkAAAAIoORBAIsAABCANABAA=}#}取z 则y x 3 此时n 3 分
=1, =2, = , =( ,2,1), ……………………………………… 12
2 2
又平面ABC的一个法向量为m 分
=(0,0,1), ……………………………………… 13
记平面DEF与平面ABC夹角为θ
,
m n
则 θ | · | 1 2 29. 分
cos = m n = = …………………………………………… 14
| || | 9 29
+4+1
4
故平面DEF与平面ABC夹角的余弦值为2 29. 分
………………………………… 15
29
. 分
18 (17 )
解 当a 时 f x x2 x
:(1) =1 , ( )= (ln +1),
f 分
∴ (1)= 1, …………………………………………………………………………… 1
又f′ x x x 分
( )= (2ln +3), ……………………………………………………………… 2
f′ 分
∴ (1)= 3,…………………………………………………………………………… 3
f x 在 f 处的切线方程为 x y . 分
∴ ( ) (1, (1)) 3 - -2=0 …………………………………… 4
x
(2)∵ ∈(0,+∞),
f′ x x x a x x x a 分
( )= 2 (ln + )+ = (2ln +2 +1),……………………………………………… 5
令φ x x a
( )= 2ln +2 +1,
φ′ x 2
( )= x >0,
φ x 在 上单调递增 分
∴ ( ) (0,+∞) , …………………………………………………… 6
由φ x x a 得x - a - 1 分
( )= 2ln +2 +1=0 =e 2, ……………………………………………… 7
f x 在 - a - 1 上单调递减 在 - a - 1 上单调递增. 分
∴ ( ) (0,e 2) , (e 2,+∞) ……………………… 9
f - a x - a 时 f x
(3)∵ (e )= 0, ∴ ∈(0,e ) , ( )<0,
x - a - 1 x - a 分
∴ 0< 1<e 2< 2<e , ……………………………………………………………… 10
x a 1 x a
∴ ln 1<- - <ln 2<- ,
2
即 x a x a 分
2(ln 1+ )<-1<2(ln 2+ )<0, ………………………………………………… 11
由f x f x 得
( 1)= ( 2) ,
x 2 x a x 2 x a
1 (ln 1+ )= 2 (ln 2+ ),
即 e ln x 1 2 (ln x 1+ a )e 2 a =e ln x 2 2 (ln x 2+ a )e 2 a ,
∴ e
2(ln x 1+ a )
·2(ln
x
1+
a
)=e
2(ln x 2+ a )
·2(ln
x
2+
a
), ……………………………………… 13
分
令t x a t x a
1=2(ln 1+ ), 2=2(ln 2+ ),
设g t t t t
( )= e , ∈(-∞,0),
g′ t t t. 分
∴ ( )=( +1)e ………………………………………………………………… 14
数学试题答案 第 页 共 页
4 ( 6 )
{#{QQABAYQQggiAABJAAAhCQw0YCEEQkAAAAIoORBAIsAABCANABAA=}#}t 时 g′ t g t 单调递减
∴ ∈(-∞,-1) , ( )<0, ( ) ,
t 时 g′ t g t 单调递增
∈(-1,0) , ( )>0, ( ) ,
下面证明t t 又t 即证t t
1+ 2<-2, 2>-1, 1<-2- 2<-1,
即证g t g t
( 1)> (-2- 2),
即证g t g t 分
( 2)> (-2- 2),……………………………………………………………… 15
令G t g t g t t
( )= ( )- (-2- ), ∈(-1,0),
G′ t g′ t g′ t t t e-2- t
( )= ( )- (-2- )=( +1)(e - )>0,
G t 在 上单调递增 分
∴ ( ) (-1,0) ,……………………………………………………… 16
G t G 从而得证
∴ ( )> (-1)= 0, ,
故 x a x a
2(ln 1+ )+2(ln 2+ )<-2,
即 x x a
ln 1 2<-2 -1,
x x -2 a -1
∴ 0< 1 2<e ,
1 2 a +1. 分
∴ x x >e ………………………………………………………………………… 17
1 2
. 分
19 (17 )
解 设动圆C的半径为r 易知圆C 和圆C 的半径分别为
(1) : , 1 2 5 2, 2,
C与C C 都内切 则
∵ 1, 2 ,
CC r CC r 分
| 1|=5 2- ,| 2|= - 2, ……………………………………………………… 1
CC CC r r 分
∴ | 1|+| 2|=5 2- + - 2=4 2, ……………………………………………… 2
又C C C C 分
1(-2,0), 2(2,0),∴ | 1 2|=4<4 2,………………………………………… 3
点C的轨迹是C C 为焦点的椭圆 分
∴ 1, 2 , …………………………………………… 4
x2 y2
设E的方程为 a b 则
:a2 +b2 =1( > >0),
a c
2 =4 2,2 =4,
a2 b2 a2 c2
∴ =8, = - =4,
x2 y2
E的方程为 . 分
∴ : + =1 …………………………………………………………… 5
8 4
证明 设A x y B x y P t t
(2)(i) : ( 1, 1), ( 2, 2), (8, )( ≠0),
x x y y
则结合圆锥曲线的性质 知直线PA的方程为 1 1 分
, + =1,………………………… 6
8 4
x x y y
直线PB的方程为 2 2 分
+ =1, ……………………………………………………… 7
8 4
ty ty
又直线PA PB都过点P t 则x 1 x 2 分
, (8, ), 1+ =1, 2+ =1,…………………………… 8
4 4
ty
因此直线AB的方程为x 显然当y 时 x 分
+ =1, =0 , =1, …………………………… 9
4
数学试题答案 第 页 共 页
5 ( 6 )
{#{QQABAYQQggiAABJAAAhCQw0YCEEQkAAAAIoORBAIsAABCANABAA=}#}直线AB过定点 . 分
∴ (1,0) …………………………………………………………… 10
设AB方程为 x my m
(ii) : = +1( ≠0),
{x my
联立 = +1 m2 y2 my 分
x2 y2 ,∴ ( +2) +2 -7=0,………………………………………… 11
+2 =8
m
y y 2 y y -7 分
∴ 1+ 2=-m2 , 1 2=m2 ,……………………………………………………… 12
+2 +2
又A′ x y
( 1,- 1),
y y
直线A′B方程为y y 1+ 2 x x 令y 得
+ 1=x x ( - 1), =0
2- 1
x y x y
x 1 2+ 2 1
M = y y
1+ 2
my y my y
( 1+1) 2+( 2+1) 1
= y y
1+ 2
my y y y y y
2 1 2+( 1+ 2) m 1 2
= y y =2 ·y y +1
1+ 2 1+ 2
-7
m2
m +2 分
=2 · m +1=8,……………………………………………………………… 14
2
-m2
+2
M 又C
∴ (8,0), 2(2,0),
S S 1 C M y y
∴ | 1- 2|= | 2 ||| 1|-| 2||
2
y y
=3| 1+ 2|
m
6| | 6
=m2 =
+2 m 2
| |+ m
| |
6 3 2 分
≤ = , …………………………………………………………… 16
2 2 2
S S 的最大值为3 2 当且仅当 m 2 即m 时取等号. 分
∴ | 1- 2| , | |= m , =± 2 ………… 17
2 | |
数学试题答案 第 页 共 页
6 ( 6 )
{#{QQABAYQQggiAABJAAAhCQw0YCEEQkAAAAIoORBAIsAABCANABAA=}#}