宣城市2023-2024学年度第二学期期末调研测试高一数学试题word版_2024-2025高一（7-7月题库）_2024年8月试卷_0815安徽省宣城市2023-2024学年高一下学期期末调研测试

宣城市 2023-2024 学年度第二学期期末调研测试 高一数学试题 考生注意事项： 1.本试卷满分 150 分，考试时间 120 分钟。 2.答题前，考生先将自己的姓名、考号在答题卷指定位置填写清楚并将条形码粘贴在指定区域。 3.考生作答时，请将答案答在答题卷上，选择题每小题选出答案后，用 2B 铅笔把答题卷上对应题目的答 案标号涂黑；非选择题请用0.5 毫米的黑色墨水签字笔在答题卷上各题的答题区域内作答，超出答题区域 书写的答案无效，在试题券、草稿纸上作答无效。 4. 考试结束时，务必将答题卡交回。 一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目 要求的. 1.已知某位自行车赛车手在相同条件下进行了8次测速，测得其最大速度(单位：m/s)的数据分别为 42， 38，45，43，41，47，46，44，则这组数据中的 75%分位数是 A. 44.5 B.45 C.45.5 D.46 2.在△ABC 中，角A，B，C所对的边分别为a，b，c，若sinA =2sinC，2b=3c，则 = A.2 B. 3 C. D. 3.若向量 ， 满足 =(1，1)，| |=1，且(  )· =0，则 与 的夹角为 A.30° B.45° C.60° D.120° 4.一个人连续射击2次，则下列各事件关系中，说法正确的是 A.事件“恰有一次击中”与事件“两次均击中”为互斥事件 B.事件“至少一次击中”与事件“至多一次击中”为互斥事件 C.事件“两次均击中”与事件“至少一次击中”互为对立事件 D.事件“两次均未击中”与事件“至多一次击中”互为对立事件 5.在△ABC中，已知D是BC边上靠近点B的三等分点，E是AC的中点，且 ，则 = A. B.1 C. D. 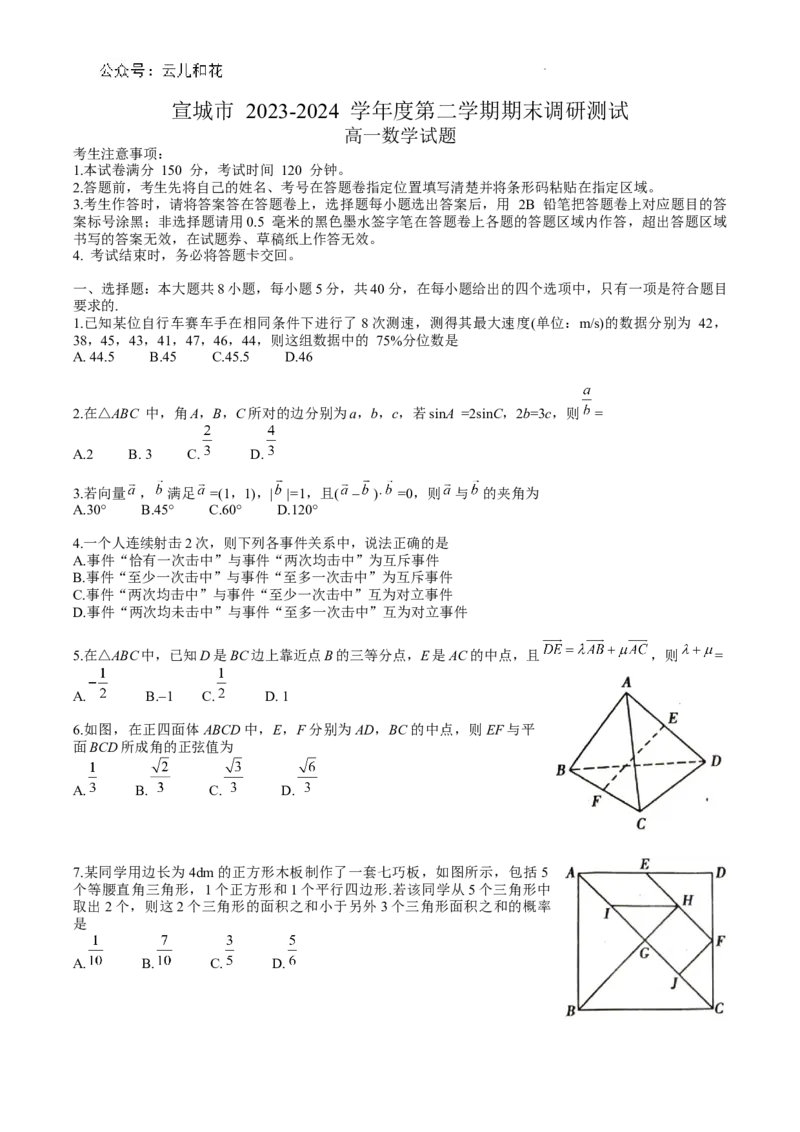1 6.如图，在正四面体ABCD中，E，F分别为AD，BC的中点，则EF与平 面BCD所成角的正弦值为 A. B. C. D. 7.某同学用边长为4dm的正方形木板制作了一套七巧板，如图所示，包括 5 个等腰直角三角形，1个正方形和1个平行四边形.若该同学从5个三角形中 取出2个，则这2个三角形的面积之和小于另外3个三角形面积之和的概率 是 A. B. C. D. 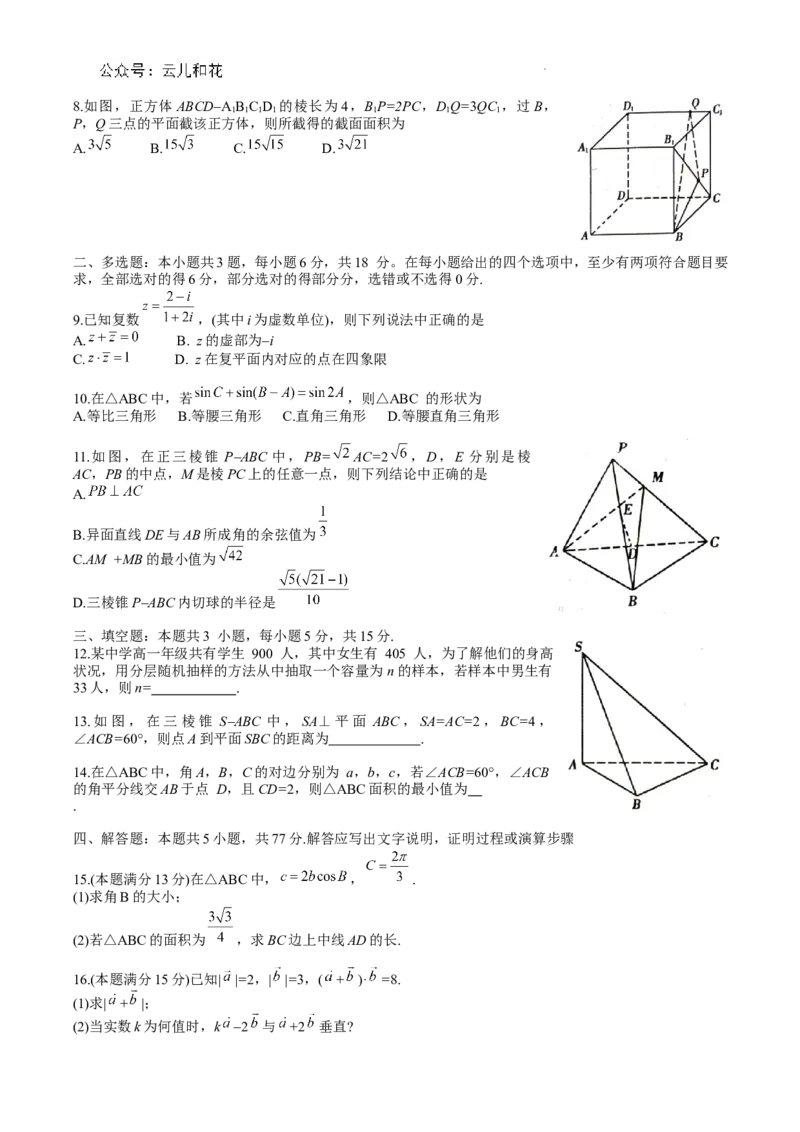学科网（北京）股份有限公司8.如图，正方体ABCDAB C D 的棱长为4，BP=2PC，DQ=3QC ，过B， 1 1 1 1 1 1 1 P，Q三点的平面截该正方体，则所截得的截面面积为 A. B. C. D. 二、多选题：本小题共3题，每小题6分，共18 分。在每小题给出的四个选项中，至少有两项符合题目要 求，全部选对的得6分，部分选对的得部分分，选错或不选得0分. 9.已知复数 ，(其中i为虚数单位)，则下列说法中正确的是 A. B. z的虚部为i C. D. z在复平面内对应的点在四象限 10.在△ABC中，若 ，则△ABC 的形状为 A.等比三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形 11.如图，在正三棱锥 PABC 中，PB= AC=2 ，D，E 分别是棱 AC，PB的中点，M是棱PC上的任意一点，则下列结论中正确的是 A. B.异面直线DE与AB所成角的余弦值为 C.AM +MB的最小值为 D.三棱锥PABC内切球的半径是 三、填空题：本题共3 小题，每小题5分，共15分. 12.某中学高一年级共有学生 900 人，其中女生有 405 人，为了解他们的身高 状况，用分层随机抽样的方法从中抽取一个容量为 n的样本，若样本中男生有 33人，则n= . 13.如图，在三棱锥 SABC 中，SA⊥平面 ABC，SA=AC=2，BC=4， ∠ACB=60°，则点A到平面SBC的距离为 . 14.在△ABC中，角A，B，C的对边分别为 a，b，c，若∠ACB=60°，∠ACB 的角平分线交AB于点 D，且CD=2，则△ABC面积的最小值为 . 四、解答题：本题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤 15.(本题满分13分)在△ABC中， ， . (1)求角B的大小； (2)若△ABC的面积为 ，求BC边上中线AD的长. 16.(本题满分15分)已知| |=2，| |=3，( + )· =8. (1)求| + |； (2)当实数k为何值时，k 2 与 +2 垂直? 学科网（北京）股份有限公司(3)若 ， 不共线，k  与4 k 反向，求实数k的值. 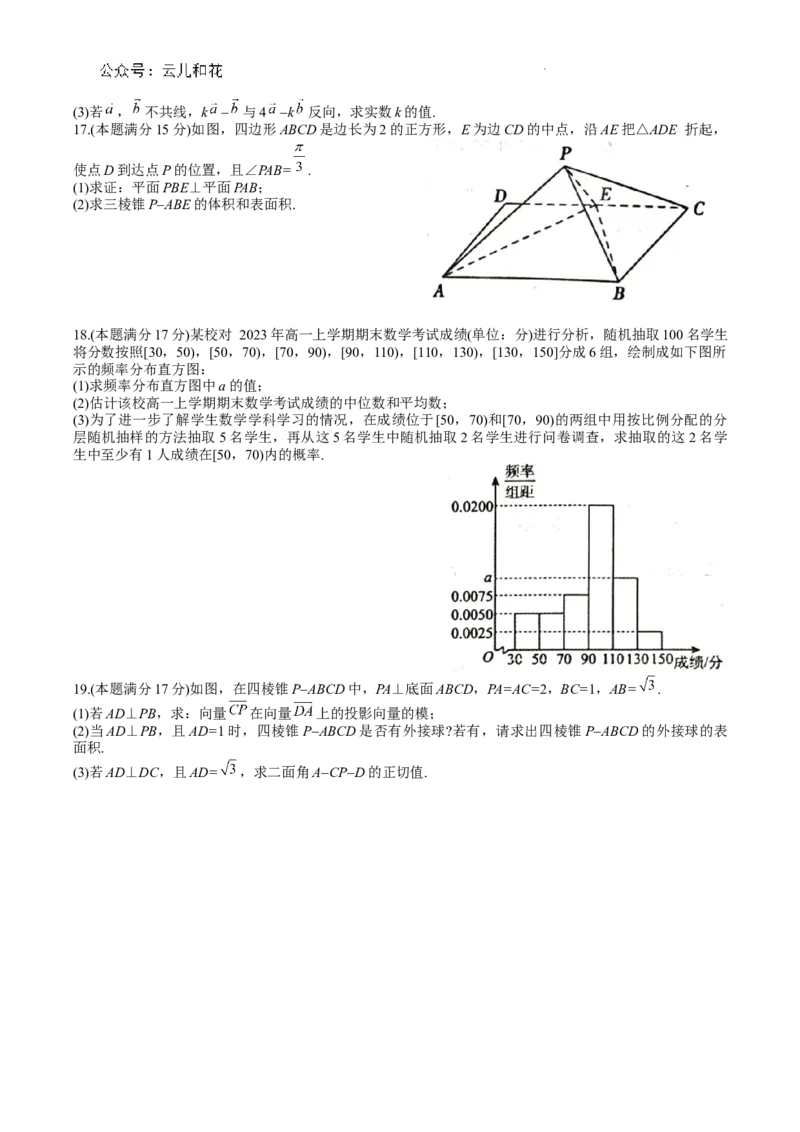17.(本题满分15分)如图，四边形ABCD是边长为2的正方形，E为边CD的中点，沿AE把△ADE 折起， 使点D到达点P的位置，且∠PAB= . (1)求证：平面PBE⊥平面PAB； (2)求三棱锥PABE的体积和表面积. 18.(本题满分17分)某校对 2023年高一上学期期末数学考试成绩(单位：分)进行分析，随机抽取100名学生 将分数按照[30，50)，[50，70)，[70，90)，[90，110)，[110，130)，[130，150]分成6组，绘制成如下图所 示的频率分布直方图： (1)求频率分布直方图中a的值； (2)估计该校高一上学期期末数学考试成绩的中位数和平均数； (3)为了进一步了解学生数学学科学习的情况，在成绩位于[50，70)和[70，90)的两组中用按比例分配的分 层随机抽样的方法抽取5名学生，再从这5名学生中随机抽取2名学生进行问卷调查，求抽取的这2名学 生中至少有1人成绩在[50，70)内的概率. 19.(本题满分17分)如图，在四棱锥PABCD中，PA⊥底面ABCD，PA=AC=2，BC=1，AB= . (1)若AD⊥PB，求：向量 在向量 上的投影向量的模； (2)当AD⊥PB，且AD=1时，四棱锥PABCD是否有外接球?若有，请求出四棱锥PABCD的外接球的表 面积. (3)若AD⊥DC，且AD= ，求二面角ACPD的正切值. 学科网（北京）股份有限公司