文档内容
2023—2024 学年度第二学期教学质量检查
高一数学
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.
.
1 已知向量 ,若 ,则 ( )
A. 2 B. C. -2 D.
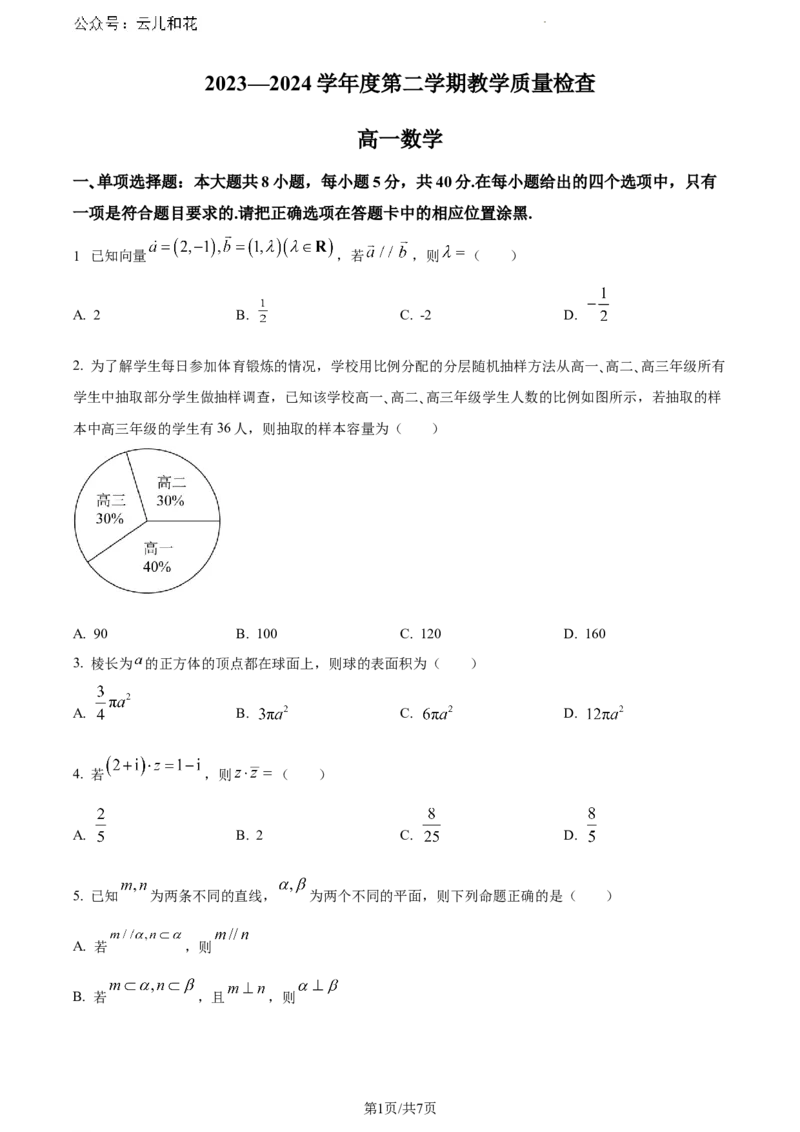
2. 为了解学生每日参加体育锻炼的情况,学校用比例分配的分层随机抽样方法从高一、高二、高三年级所有
学生中抽取部分学生做抽样调查,已知该学校高一、高二、高三年级学生人数的比例如图所示,若抽取的样
本中高三年级的学生有36人,则抽取的样本容量为( )
A. 90 B. 100 C. 120 D. 160
3. 棱长为 的正方体的顶点都在球面上,则球的表面积为( )
A. B. C. D.
4. 若 ,则 ( )
A. B. 2 C. D.
5. 已知 为两条不同的直线, 为两个不同的平面,则下列命题正确的是( )
A. 若 ,则
B. 若 ,且 ,则
第1页/共7页
学科网(北京)股份有限公司C. 若 , ,则
D. 若 ,则
6. 已知向量 ,且 ,任意点 关于点 的对称点为 ,点 关于点 的
对称点为 ,则 ( )
A. B. 6 C. D. 3
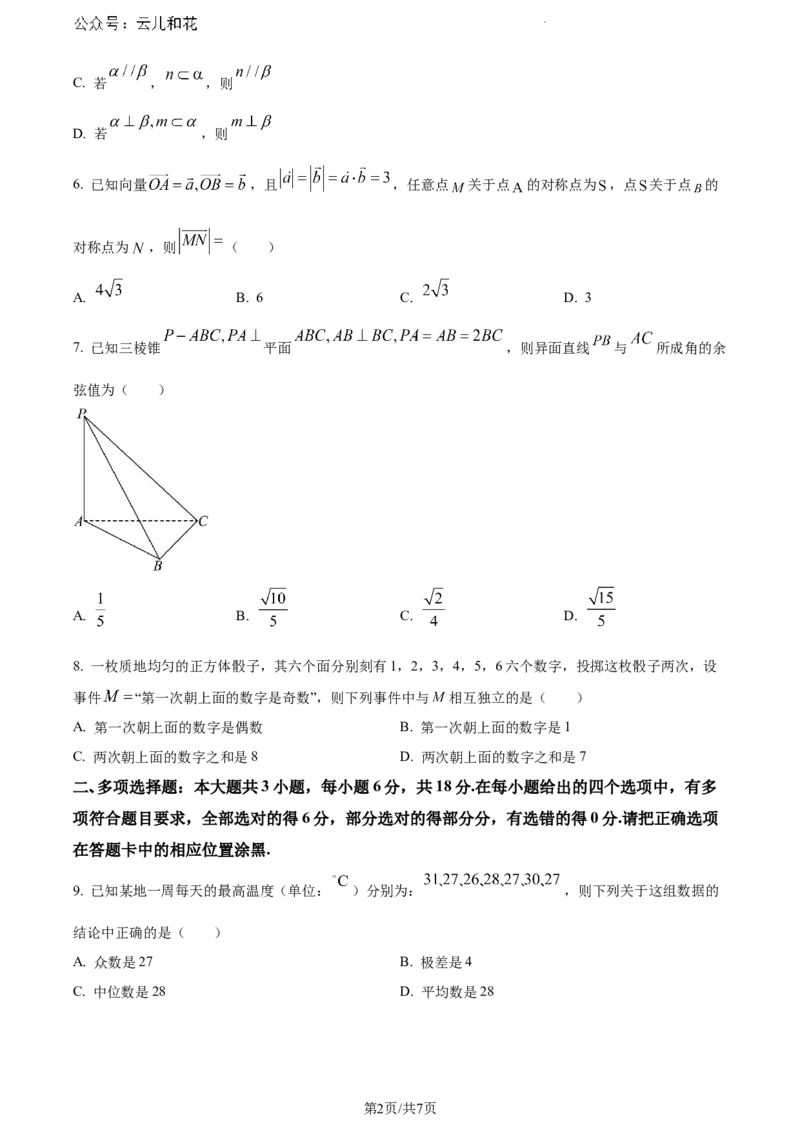
7. 已知三棱锥 平面 ,则异面直线 与 所成角的余
弦值为( )
A. B. C. D.
8. 一枚质地均匀的正方体骰子,其六个面分别刻有1,2,3,4,5,6六个数字,投掷这枚骰子两次,设
事件 “第一次朝上面的数字是奇数”,则下列事件中与 相互独立的是( )
A. 第一次朝上面的数字是偶数 B. 第一次朝上面的数字是1
C. 两次朝上面的数字之和是8 D. 两次朝上面的数字之和是7
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.请把正确选项
在答题卡中的相应位置涂黑.
9. 已知某地一周每天的最高温度(单位: )分别为: ,则下列关于这组数据的
结论中正确的是( )
A. 众数是27 B. 极差是4
C. 中位数是28 D. 平均数是28
第2页/共7页
学科网(北京)股份有限公司10. 已知 的半径为 为其内接三角形,则下列结论中正确的是( )
A. 若 ,则
B. 若 ,则 周长的最大值为
C. 若 ,则
D. 若 ,则 面积的最大值为
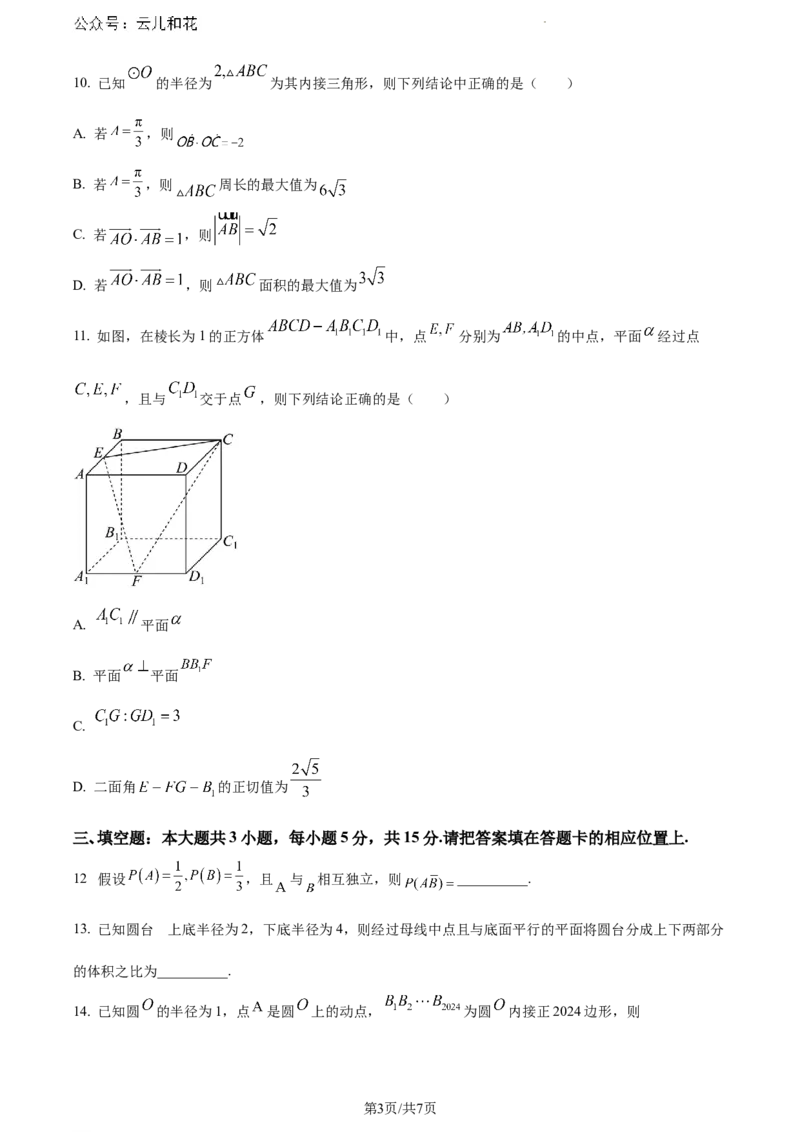
11. 如图,在棱长为1的正方体 中,点 分别为 的中点,平面 经过点
,且与 交于点 ,则下列结论正确的是( )
A. 平面
B. 平面 平面
C.
D. 二面角 的正切值为
三、填空题:本大题共3小题,每小题5分,共15分.请把答案填在答题卡的相应位置上.
.
12 假设 ,且 与 相互独立,则 __________.
的
13. 已知圆台 上底半径为2,下底半径为4,则经过母线中点且与底面平行的平面将圆台分成上下两部分
的体积之比为__________.
14. 已知圆 的半径为1,点 是圆 上的动点, 为圆 内接正2024边形,则
第3页/共7页
学科网(北京)股份有限公司__________, __________.
四、解答题:本大题共5小题,第15题13分,16、17题15分,18、19题17分,共77分.解答
应写出文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,
超出指定区域的答案无效.
的
15. 已知 分别为 三个内角 对边,且 .
(1)求角 ;
的
(2)若 ,求 面积.
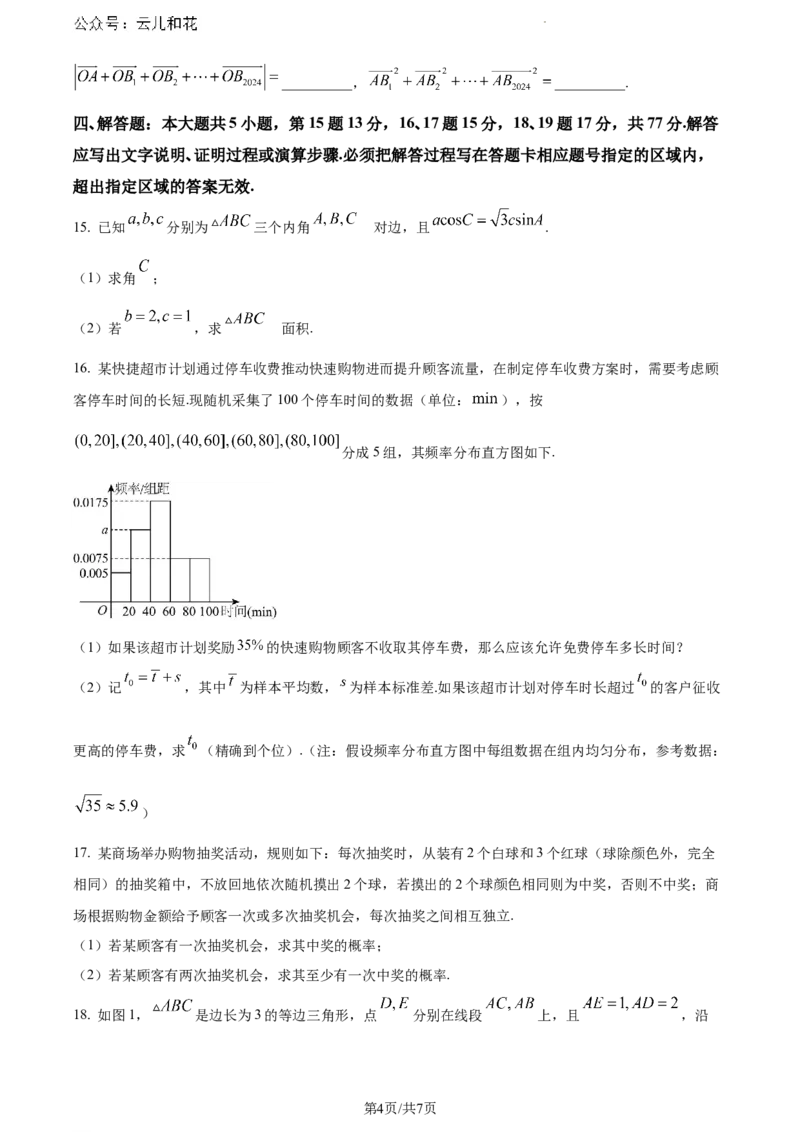
16. 某快捷超市计划通过停车收费推动快速购物进而提升顾客流量,在制定停车收费方案时,需要考虑顾
客停车时间的长短.现随机采集了100个停车时间的数据(单位: ),按
分成5组,其频率分布直方图如下.
(1)如果该超市计划奖励 的快速购物顾客不收取其停车费,那么应该允许免费停车多长时间?
(2)记 ,其中 为样本平均数, 为样本标准差.如果该超市计划对停车时长超过 的客户征收
更高的停车费,求 (精确到个位).(注:假设频率分布直方图中每组数据在组内均匀分布,参考数据:
)
17. 某商场举办购物抽奖活动,规则如下:每次抽奖时,从装有2个白球和3个红球(球除颜色外,完全
相同)的抽奖箱中,不放回地依次随机摸出2个球,若摸出的2个球颜色相同则为中奖,否则不中奖;商
场根据购物金额给予顾客一次或多次抽奖机会,每次抽奖之间相互独立.
(1)若某顾客有一次抽奖机会,求其中奖的概率;
(2)若某顾客有两次抽奖机会,求其至少有一次中奖的概率.
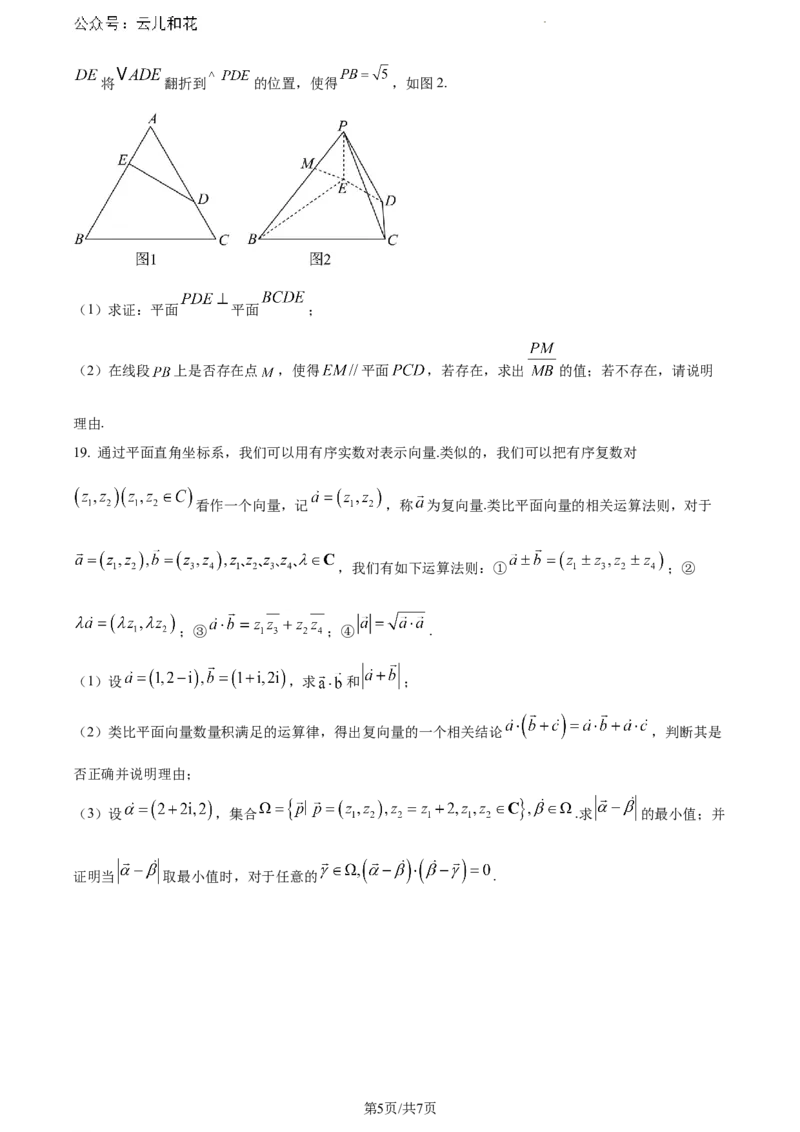
18. 如图1, 是边长为3的等边三角形,点 分别在线段 上,且 ,沿
第4页/共7页
学科网(北京)股份有限公司将 翻折到 的位置,使得 ,如图2.
(1)求证:平面 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ,若存在,求出 的值;若不存在,请说明
理由.
19. 通过平面直角坐标系,我们可以用有序实数对表示向量.类似的,我们可以把有序复数对
看作一个向量,记 ,称 为复向量.类比平面向量的相关运算法则,对于
,我们有如下运算法则:① ;②
;③ ;④ .
(1)设 ,求 和 ;
(2)类比平面向量数量积满足的运算律,得出复向量的一个相关结论 ,判断其是
否正确并说明理由;
(3)设 ,集合 .求 的最小值;并
证明当 取最小值时,对于任意的 .
第5页/共7页
学科网(北京)股份有限公司2023—2024 学年度第二学期教学质量检查
高一数学
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.
【1题答案】
【答案】D
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】A
【5题答案】
【答案】C
【6题答案】
【答案】A
【7题答案】
【答案】B
【8题答案】
【答案】D
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.请把正确选项
在答题卡中的相应位置涂黑.
【9题答案】
【答案】AD
【10题答案】
【答案】ABC
【11题答案】
【答案】BCD
三、填空题:本大题共3小题,每小题5分,共15分.请把答案填在答题卡的相应位置上.
【12题答案】
第6页/共7页
学科网(北京)股份有限公司【答案】
【13题答案】
【答案】
【14题答案】
【答案】 ①. 1 ②. 4048
四、解答题:本大题共5小题,第15题13分,16、17题15分,18、19题17分,共77分.解答
应写出文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,
超出指定区域的答案无效.
【15题答案】
【答案】(1)
(2)
【16题答案】
【答案】(1)40分钟 (2)74
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)证明见解析
(2)存在,
【19题答案】
【答案】(1) ;
(2)答案见解析 (3)答案见解析
第7页/共7页
学科网(北京)股份有限公司