文档内容
东莞市 2024-2025 学年第二学期七校联考试题高一数学
一、单项选择题(本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.若复数z满足1+iz=i,则z的虚部为( )
A.−1 B.1 C.−i D.i
2.已知向量 ,且 则 ( )
⃗a=(2,1),⃗b=(λ,λ−1) ⃗a//⃗b, λ=
1 1 2
A.− B. C. D.2
2 3 3
3.如图,△O' A'B'是水平放置的△OAB的直观图,O' A'=2,O'B'=3,∠A'O'B'=45°,则原
△AOB的面积为( )
A.3√2 B.4√2 C.6 D.8
4.在三角形ABC中,分别根据下列条件解三角形,其中有两解的是( )
A.a=8,b=16,A=30° B.a=25,b=30,A=150°
C.a=30,b=40,A=30° D.a=72,b=30,A=45°
5.中国古代四大名楼鹳雀楼,位于山西省运城市永济市蒲州镇,因唐代诗人王之涣的诗作
《登鹳雀楼》而流芳后世.如图,某同学为测量鹳雀楼的高度MN,在鹳雀楼的正东方向找到
一座建筑物AB,高约为35m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A,鹳雀
楼顶部M的仰角分别为30°和45°,在A处测得楼顶部M的仰角为15°,则鹳雀楼的高度约为
( )
A.70m B.64m C.52m D.91m
6.将半径为4的半圆面围成一个圆锥,则该圆锥的体积为( )
8√3 16√3
A.8√3π B. π C.16√3π D. π
3 37.如果向量⃗a,⃗b的夹角为θ,我们就称⃗a×⃗b为向量⃗a与⃗b的“向量积”,⃗a×⃗b还是一个向量,
它的长度为 .在棱长为2的正方体 中,则
|⃗a×⃗b|=|⃗a|⋅|⃗b|sinθ ABCD−A B C D
1 1 1 1
( )
|⃗AD ×⃗DB|=
1
A.−4√3 B.−4 C.4 D.4√3
8.在直三棱柱ABC−A B C 中,AB=AC=2, AB⊥AC,若该棱柱外接球的表面积为12π,
1 1 1
则侧面BB C C绕直线BB 旋转一周所得到的旋转体的体积为( )
1 1 1
A.12π B.16π C.20π D.24π
二、多项选择题(本大题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选项中,
有多个选项符合题目要求,全部选对得 6 分,选错或不选得 0 分,部分选对的得部分
分.)
9.已知复数z满足: ,则( )
z(1+i)=6i5
A.|z|=3√2 B.z的虚部是3
C.z−z=6i D.复数z在复平面内对应的点位于第四象限
10.如图,在边长为6的等边△ABC中,⃗CD=2⃗DB,⃗AE=⃗ED,点P在以AB为直径的半圆上
(不含点A,B),则下列结论正确的是( )
A.⃗AB⋅⃗AC=18 B.⃗PA⋅⃗PB=0
1 1 5
C.⃗BE= ⃗AB+ ⃗AC D.⃗AD在⃗AB上的投影向量为 ⃗AB
3 6 6
11.如图所示,在棱长为2的正方体ABCD−A B C D 中,E、F分别为AB,BC的中点,则
1 1 1 1
( )A.EF⊥BD
1
B.EF//平面A D B
1 1
π
C.直线BD 与平面ABCD所成的角为
1 4
D.三棱锥B −EBF外接球表面积为6π
1
三、填空题(本大题共 3 小题,每小题 5 分,共 15 分,其中第14题第一空3分,第二空
2分.把答案填在答题卡中的横线上.)
12.已知向量⃑a,⃑b满足|⃑a| =1,|⃑b| =2,且⃑a⊥(⃑a+⃑b),则⃑a与⃑b的夹角为 .
13.《九章算术》中将圆台称为“圆亭”.已知某圆亭的高为3,上底面半径为1,下底面半
径为5,则此圆亭的表面积等于 .
14.我国南宋时期杰出数学家秦九韶在《数书九章》中提出了“三斜求积术”,即以小斜幂,
并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一
为从隅,开平方得积,把以上文字写出公式,即 √1 c2+a2−b2 2 (其中 为三角形
S= [c2a2−( ) ] S
4 2
面积,a,b,c为三角形的三边). 在非直角△ABC中,a,b,c为内角A,B,C所对应的
三边,若 且 ,则 面积的最大值是 ,此时 外接圆
a=3 a=c(cosB+√3cosC) △ABC △ABC
的半径为
.
四、解答题(本大题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.)
15.(13分)已知复数z=3+mi,其中m∈R.
(1)设z =(1+3i)z,若z 是纯虚数,求实数m的值;
1 1
(2)设m=−1,分别记复数z、z2在复平面上对应的点为A、B,求⃗OA与⃗OB的夹角余弦值以及
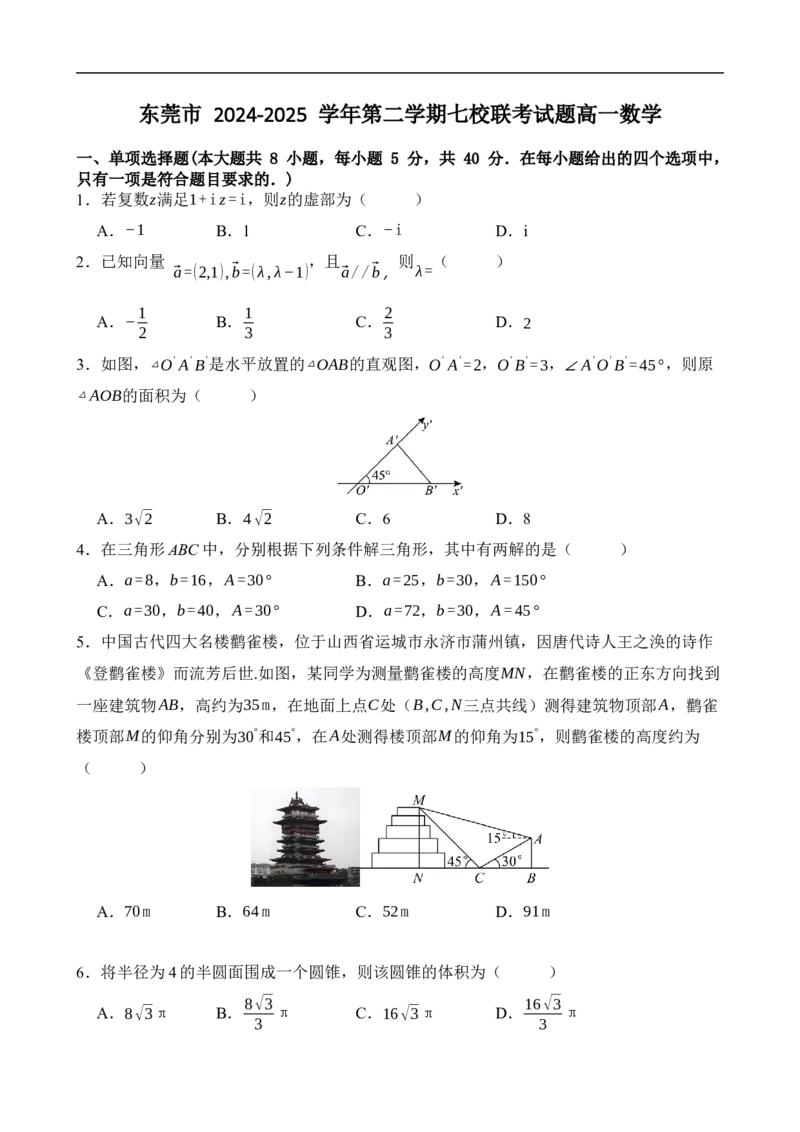
⃗OA在⃗OB上的投影向量.16.(15分)已知在△ABC中,内角A,B,C的对边分别为a,b,c,且满足
ccosB+bcosC=a2.
π √3
(1)求a; (2)若A= ,且S = ,求△ABC的周长.
3 △ABC 4
17.(15分)如图,△ABC中,⃗CA=⃗a,⃗CB=⃗b,D是AC的中点,⃗CB=2⃗BE,AB与DE交于点M.
(1)用⃗a,⃗b表示⃗DE;
(2)设⃗BM=λ⃗BA,求λ的值;
(3)若⃗AB⊥⃗DE,求∠ACB的最大值.
18.(17分)如图,在四棱锥P−ABCD中,PD⊥平面ABCD, AB//DC,
AD⊥DC,DA=AB=PD=2,DC=4, E,F分别为棱CD,PD的中点.
(1) 求证:PB//平面AEF;
(2) 求证:AE⊥平面PBD;
(3) 求点D到平面PBC的距离.
19.
20. (17分)在△ABC中,内角A,B,C对应的边分别为a,b,c,
sin2A+cos2B+cos2C+sinBsinC=2.
(1)求A;
(2)若b=1,c=2,D为线段BC内一点,且BD:DC=1:2,求线段AD的长;
(3)法国著名科学家柯西在数学领域有非常高的造诣;很多数学的定理和公式都以他的名字
来命名,如对于任意的 ,都有 被称为柯西不
x ,x ,y ,y ∈R (x x + y y ) 2≤ (x2+ y2 )(x2+ y2 )
1 2 1 2 1 2 1 2 1 1 2 22 1 1
(a2+b2+c2 )[ + + ]
等式;若a=2,求: 1−cos2A cos2 ( π −B) sin2 (π+C) 的最小值.
2东莞市 2024-2025 学年第二学期七校联考试题(高一数学)参考答案:
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B D C C A B D B AC ABD AD
12. 13. 14.
15.(13分)
(1) ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
2
因为 是纯虚数,所以 且 ,解得 ; ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
(2)当 时, ,故 ,
5
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
,故 .
7
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
设 ,则 ;
9
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
11
所以 在 上的数量投影向量为 .⋯⋯⋯⋯
13
分
16.(15分)
(1)已知 ,
则由正弦定理有 .
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
又∵ ,则
3
,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
5
因为 为三角形内角,则 , .
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
7
(2)由题可知: ,所以 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
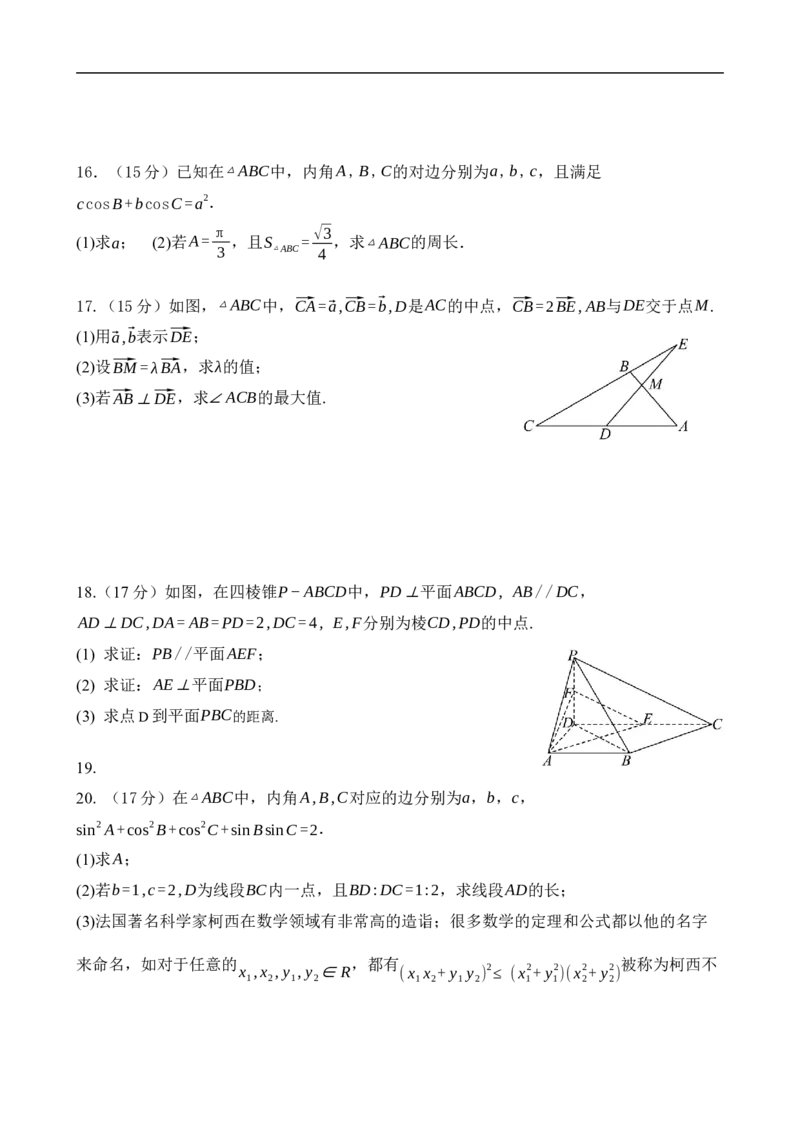
10由余弦定理可得 ,即 , ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
1
所
2
以 ,可得 ,则 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
所以 的周长为 .
14
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
15
17.(15分)
(1) .
分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
(2)
⋯3
分
因为 三点共线,所以 ,解得 .
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7
分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9
(2) ,由(1)可知 ,所以 ,⋯⋯⋯⋯⋯⋯⋯⋯
分
11
得 ,则 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
12
所以 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
所以 的最大值为 .
14
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
18.(17分)
15
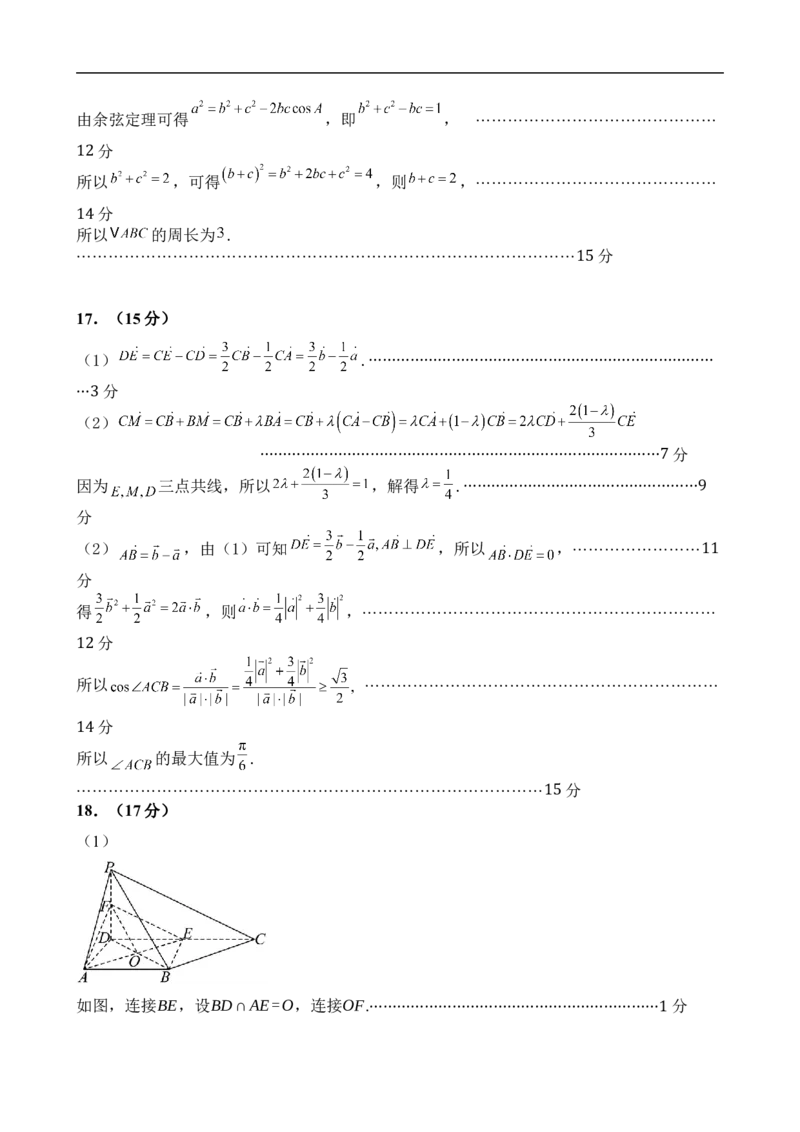
(1)
如图,连接BE,设BD∩AE=O,连接OF. 分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11
因AB//DC,DE= DC=AB=2,可得 ▱ABED,则OD=OB,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
2
2
又DF=PF,则得OF//PB,
因OF⊂平面AEF,PB⊄平面AEF,故PB//平面AEF. 分
(2)由(1)已得▱ABED,因DA=AB=2,故四边形AB
⋯
E
⋯
D为
⋯⋯
菱
⋯
形
⋯
,
⋯
则
⋯
A
⋯
E⊥
⋯⋯
BD
⋯
,
⋯⋯⋯4
因PD⊥平面ABCD, AE⊂平面ABCD,则PD⊥AE,
又BD∩PD=D,BD,PD⊂平面PBD,故AE⊥平面PBD. 分
(3)在
Rt△ABC
中,
BD=√22+22=2√2
,
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8
因PD⊥平面ABCD, BD、CD⊂平面ABCD,则PD⊥BD,PD⊥CD
在
Rt△POB
中,
PD=2,BD=2√2,PB=√22+(2√2) 2=2√3
,同理,
BC=2√2
,
PC=2√5
,
分
故满足勾股定理 PB2+BC2=PC2 ,则PB ⋯ ⊥ ⋯⋯ BC ⋯,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分
1 1
故S = PB·BC= ×2√3×2√2=2√6⋯⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ 1 ⋯ 1 分
△PBC 2 2
12
1 1 1 8
而V = S ·PD= × ×4×2×2= ,设点D到平面PBC的距离为d,
P−BCD 3 △BCD 3 2 3
1 8 2√6
由等体积法得 V = S ·d=V = , 得 d= 分
D−PBC 3 △PBC P−BCD 3 3
2√6
⋯⋯⋯⋯⋯⋯⋯⋯⋯16
故点D到平面PBC的距离为 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
3
17
19.(17分)
(1)由 ,得 ,
即 ,
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
在 中,由正弦定理得 ,
2
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
由余弦定理得 ,而 ,
4
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
所以 .
5
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
(2)由 ,得 ,
6
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 分
7则 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分
9
所以 . ⋯⋯⋯⋯⋯⋯
12
分
(3)依题意,
,
分
当且仅当 为正三角形时取等号,所以所求的最小值为48.
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16
分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯17