文档内容
专题2.4 期中真题模拟卷04(1-3 章)
一.选择题(共12小题)
1.(2020·吉林朝阳·长春外国语学校期末(文))有下列四个命题,其中真命题是
( ).
A. , B. , ,
C. , , D. ,
【答案】B
【解析】
对于选项A,令 ,则 ,故A错;
对于选项B,令 ,则 , 显然成立,故B正确;
对于选项C,令 ,则 显然无解,故C错;
对于选项D,令 ,则 显然不成立,故D错.
故选B
2.(2020·浙江) 的一个必要不充分条件是( )
A. B.C. D.
【答案】B
【解析】
求解不等式 可得 ,
结合所给的选项可知 的一个必要不充分条件是 .
本题选择B选项.
3.(2020·六盘山高级中学期末(文))下列命题中正确的是( )
A.若 ,则 B.若 ,则
C.若 , ,则 D.若 , ,则
【答案】A
【解析】
对于选项 ,若 ,所以 ,则 ,所以该选项正确;
对于选项 , 符号不能确定,所以该选项错误;
对于选项 ,设 ,所以 ,所以
该选项错误;对于选项 ,设 ,所以该选项错误;
故选:A
4.(2020·江西省奉新县第一中学月考(文))下列不等式中,正确的是( )
A.a+ ≥4 B.a2+b2≥4ab
C. ≥ D.x2+ ≥2
【答案】D
【解析】
a<0,则a+ ≥4不成立,故A错;
a=1,b=1,a2+b2<4ab,故B错,
a=4,b=16,则 < ,故C错;
由基本不等式得x2+ ≥ 2 可知D项正确.
故选:D.
5.(2020·四川省绵阳江油中学期中)已知 , , ,则
的最小值为( )A. B. C. D.
【答案】C
【解析】
解:因为 ,所以 ,即 ,
因为 , ,所以 , ,所以
当且仅当 即 , 时取等号,
故选:C
6.(2020·安徽宣城期末(理))已知m, , ,则 的最小值为(
)
A. B.7 C.8 D.4
【答案】A
【解析】∵m, , ,
∴ ,
当且仅当 且 ,即 , 时取等号,
故 的最小值 .
故选:A.
7.(2020·江西省信丰中学月考)不等式 的解集为( )
A.[0,1] B.(0,1]
C.(﹣∞,0]∪[1,+∞) D.(﹣∞,0)∪[1,+∞)
【答案】B
【解析】
根据题意, 且 ,
解得 ,
即不等式的解集为(0,1],
故选:B
8.(2020·铅山县第一中学月考)已知 , ,则 等于()
A. B. C. D.
【答案】B
【解析】
解:设 ,则 ,
, ,
解得 .
故选:B.
9.(2020·江苏宝应中学)已知定义在 上的奇函数 满足:当 时,
,若不等式 对任意实数 恒成立,则实数 的取值范围是
( )
A. B.
C. D.
【答案】A
【解析】
由于函数 为 上的奇函数,则 .当 时, ,则 .
所以,对任意的 , ,则函数 为 上的增函数.
由 可得 ,即 ,
由题意可知,不等式 对任意的实数 恒成立.
①当 时,则有 ,在 不恒成立;
②当 时,则 .
综上所述,实数 的取值范围是 .
故选:A.
10.(2020·福建省泰宁第一中学月考(理))下列函数中,既是偶函数又在区间
(0,+∞)上单调递增的是( )
A.y=x2+2x B.y=x3 C.y=lnx D.y=x2
【答案】D
【解析】
A选项:y=x2+2x是非奇非偶函数所以,所以不是偶函数,不合题意;
B选项:y=x3是奇函数,不合题意;
C选项:y=lnx是非奇非偶函数,所以不是偶函数,不合题意;
D选项:y=x2既是偶函数又在区间(0,+∞)上单调递增.
故选:D11.(2020·洛阳市第一高级中学月考(理))已知函数 是幂函
数,对任意的 且 ,满足 ,若
,则 的值( )
A.恒大于0 B.恒小于0 C.等于0 D.无法判断
【答案】B
【解析】
由题可知:函数 是幂函数
则 或
又对任意的 且 ,满足
所以函数 为 的增函数,故
所以 ,又 ,
所以 为 单调递增的奇函数
由 ,则 ,所以
则
故选:B12.(2019·甘肃酒泉月考)已知 是定义在 上的奇函数,对任意的
,均有 .当 时, ,
,则
( )
A. B. C. D.
【答案】C
【解析】
由f(x)=1-f(1-x),得 f(1)=1,
令 ,则 ,
∵当x∈[0,1]时,
∴ ,
即
,∵对任意的x,x∈[-1,1],均有(x-x)(f(x)-f(x))≥0 ,
1 2 2 1 2 1
同理 .
∵f(x)是奇函数,
∴
故选:C.
二.填空题(共6小题)
13.(2020·邢台市第八中学期末)已知条件 ;条件
,若 是 的充分不必要条件,则实数m的取值范围是
__________.
【答案】 或
【解析】
∵条件 ;∴ ,∴ 或 ,
∵条件 ,,∴ 或 ,
若 是 的充分不必要条件,则 ,解得: 或故答案为 或
14.(2020·江苏扬中市第二高级中学)已知 ,且 ,则
的最小值为_________.
【答案】4
【解析】
, ,
,当且仅当 =4时取等号,
结合 ,解得 ,或 时,等号成立.
故答案为:
15.(2020·横峰中学(理))已知正实数 , 满足 ,则 的最小
值为______.
【答案】
【解析】
正实数 , ,即 , ;
,则 ,
那么:
当且仅当 时,即取等号.
的最小值为: ,
故答案为: .
16.(2020·浙江)若 对 恒成立,则实数 的取值范围
为______.
【答案】
【解析】
因为 对 恒成立,
当 时, 或 恒成立,
因此 ;当 时, 恒成立,
因此 ;
综上:
故答案为:
17.(2020·甘谷县第四中学月考(文)) 已知函数 是幂函
数,且 在 上单调递增,则实数 ________.
【答案】2
【解析】
由题意,函数 是幂函数,
可得 ,即 ,解得 或 ,
当 时,函数 ,此时 在 上单调递增,符合题意;
当 时,函数 ,此时 在 上单调递减,不符合题意,
故答案为: .
18.(2020·洛阳市第一高级中学月考(文))已知 是定义域为 的奇函数,
满足 ,若 ,则________.
【答案】0.
【解析】
因为 是定义域为 的奇函数,
所以 且
又
所以
所以
所以函数 的周期为 ,又因为 、 ,
在 中,令 ,可得:
在 中,令 ,可得:
在 中,令 ,可得:
所以
故答案为:0.
三.解析题(共6小题)
19.(2020·安徽师范大学附属中学(文))已知函数 .(1)解不等式 ;
(2)记函数 的值域为 ,若 ,求 的最小值.
【答案】(1) ;(2)17.
【解析】
解:(1)依题意,得 于是 或
或 ,解得 .即不等式 的解集为 .
(2)证明: ,
当且仅当 时,取等号,所以 .
则 在 单调递增,
所以 .所以 的最小值为17.20.(2020·甘谷县第四中学月考(理))设 实数 满足 , 实数
满足 .
(1)若 ,且 为真,求实数 的取值范围;
(2)若其中 且 是 的充分不必要条件,求实数 的取值范围.
【答案】(1) (2)
【解析】
对于 :由 得 ,解
(1)当 时,对于 : ,解得 ,由于 为
真,所以 都为真命题,所以 解得 ,所以实数 的取值范围是
.
(2)当 时,对于 : ,解得 .由于
是 的充分不必要条件,所以 是 的必要不充分条件,所以 ,解得
.所以实数 的取值范围是 .21.(2020·福建省泰宁第一中学月考(理))已知函数 对任意 满足:
,二次函数 满足: 且 .
(1)求 , 的解析式;
(2)若 时,恒有 成立,求 的最大值.
【答案】(1)求 , ;(2) 的最大值5.
【解析】
(1) ①,
用 代替上式中的 ,
得 ②,
联立①②,可得 ;
设 ,
所以 ,
即
所以 ,解得 , ,
又 ,得 ,所以 .(2)令 ,
即
解得
所以当 时,
若要求 时,恒有 成立,
可得 ,即 的最大值是 .
22.(2019·贵溪市实验中学月考(理))已知函数 .
(1)对任意 恒成立,求实数 的取值范围:
(2)函数 ,设函数 ,若函数 有且只有两个零
点,求实数 的取值范围.
【答案】(1) ;(2) .
【解析】
解:(1) 的定义域为R,
,故函数 关于y轴对称,
当 时, ,
当 时, ,
对任意 恒成立,即有 ,
故实数 的取值范围为 .
(2)显然 不是函数 的零点.
故函数 有且只有两个零点.
与 的图象有两个交点.
当 时, ,
恒成立,
故函数 在 单调递增,在 单调递增,
且当 时, 时,函数 ,
当 时, 时,函数 ,时,函数 ,
当 时, ,
令 ,因为 ,故解得 ,
当 时, ,故在 单调递增,
当 时, ,故在 单调递减,
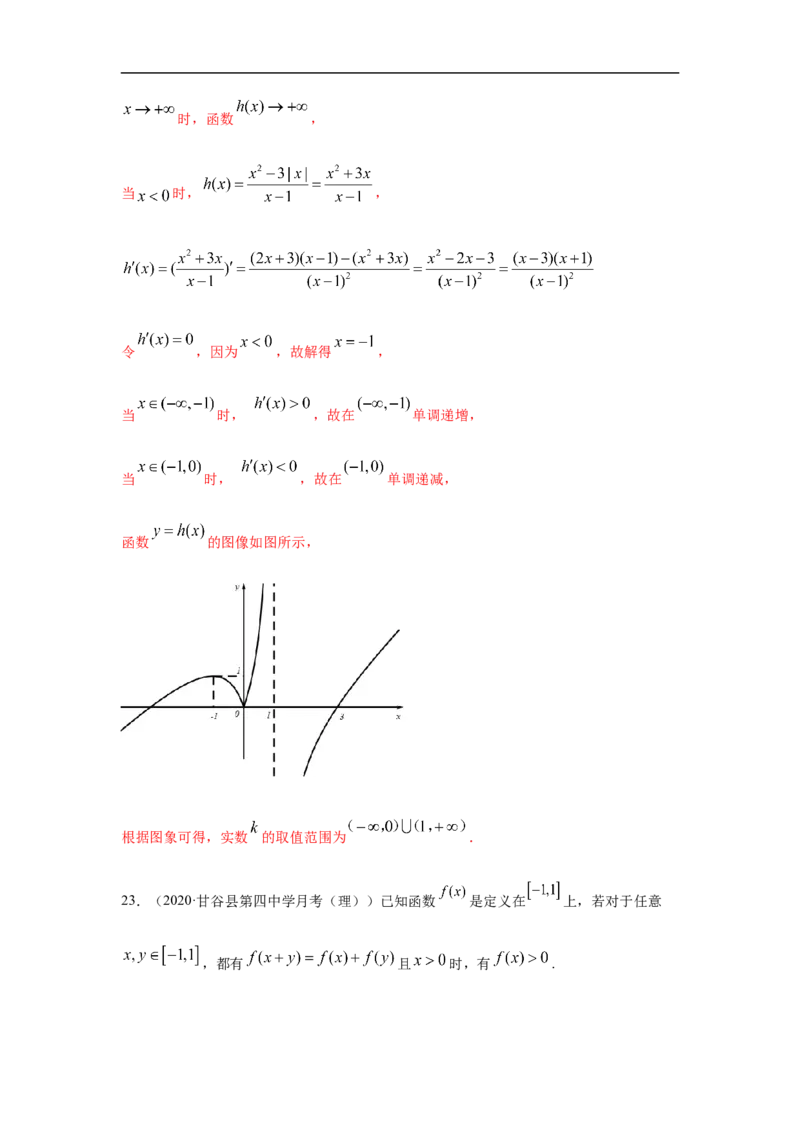
函数 的图像如图所示,
根据图象可得,实数 的取值范围为 .
23.(2020·甘谷县第四中学月考(理))已知函数 是定义在 上,若对于任意
,都有 且 时,有 .(1)证明: 在 上为奇函数,且为单调递增函数;
(2)解不等式 ;
【答案】(1)证明见解析;(2) .
【解析】
(1)证明:令 有 ,
令 , ,即 ,
所以 是奇函数.
又令 ,则 = ,
又当 时,有 , ,
∴ ,即 ,
∴ 在定义域 上为单调递增函数;
(2)∵ 在 上为单调递增的奇函数,有 ,
则 ,∴ ,即 , ,
解得不等式的解集为 .
24.(2020·郁南县连滩中学期中)已知函数 ,且 .
(1)求 的值;
(2)证明 的奇偶性;
(3)判断 在 上的单调性,并给予证明.
【答案】(1) ;(2)奇函数,证明见解析;(3)单调增函数,证明见解析.
【解析】
(1) ,解得 ;
(2)因为 ,定义域为 ,关于原点对称,
又 ,因此,函数 为奇函数;
(3)设 ,则,
因为 ,所以 ,所以 ,
因此,函数 在 上为单调增函数.