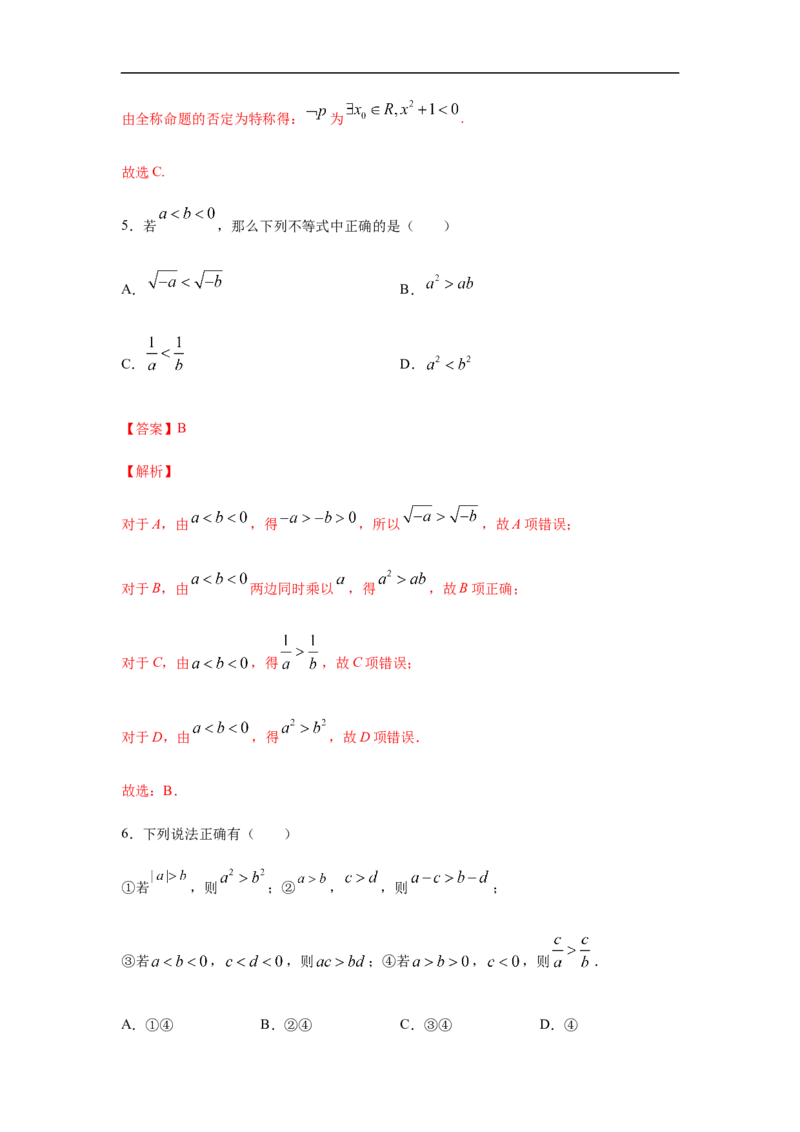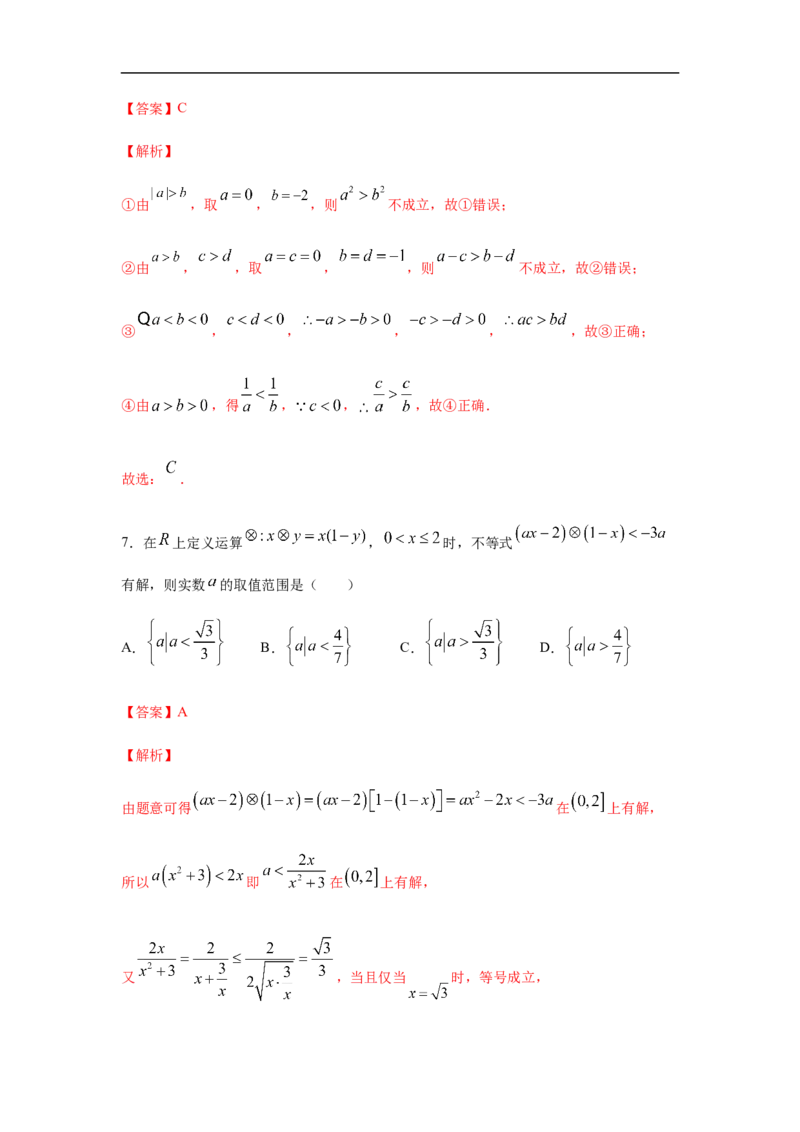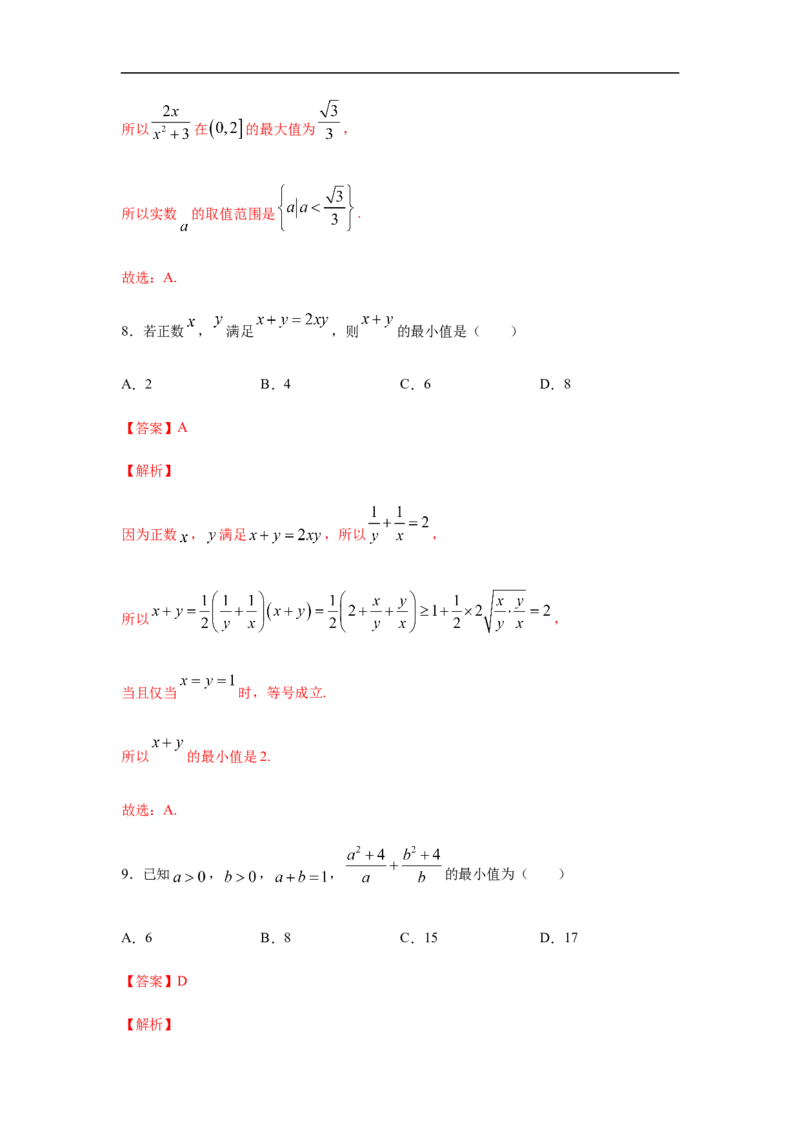文档内容
专题3.4 选择(30道)冲刺篇(期中篇)(1-3 章)
1.已知集合 , , ,则( )
A. B.
C. D.
【答案】D
【解析】
对选项A, ,故A错误;
对选项B, ,故C错误.
对选项C, ,故C错误.
对选项D, ,故D正确.
故选:D
2.已知集合 , ,则 ( )
A. B. C. D.
【答案】C【解析】
因为 ,
,
所以 ,
故选:C
3.设命题 所有正方形都是平行四边形,则 为( )
A.所有正方形都不是平行四边形 B.有的平行四边形不是正方形
C.有的正方形不是平行四边形 D.不是正方形的四边形不是平行四边形
【答案】C
【解析】
“所以”改为“存在”(或“有的”),“都是”改为“不都是”(或“不是”),
即 为有的正方形不是平行四边形
故选C.
4.命题 ,则 为( )
A. B.
C. D.
【答案】C
【解析】
命题 ,由全称命题的否定为特称得: 为 .
故选C.
5.若 ,那么下列不等式中正确的是( )
A. B.
C. D.
【答案】B
【解析】
对于A,由 ,得 ,所以 ,故A项错误;
对于B,由 两边同时乘以 ,得 ,故B项正确;
对于C,由 ,得 ,故C项错误;
对于D,由 ,得 ,故D项错误.
故选:B.
6.下列说法正确有( )
①若 ,则 ;② , ,则 ;
③若 , ,则 ;④若 , ,则 .
A.①④ B.②④ C.③④ D.④【答案】C
【解析】
①由 ,取 , ,则 不成立,故①错误;
②由 , ,取 , ,则 不成立,故②错误;
③ , , , , ,故③正确;
④由 ,得 , , ,故④正确.
故选: .
7.在 上定义运算 , 时,不等式
有解,则实数 的取值范围是( )
A. B. C. D.
【答案】A
【解析】
由题意可得 在 上有解,
所以 即 在 上有解,
又 ,当且仅当 时,等号成立,所以 在 的最大值为 ,
所以实数 的取值范围是 .
故选:A.
8.若正数 , 满足 ,则 的最小值是( )
A.2 B.4 C.6 D.8
【答案】A
【解析】
因为正数 , 满足 ,所以 ,
所以 ,
当且仅当 时,等号成立.
所以 的最小值是2.
故选:A.
9.已知 , , , 的最小值为( )
A.6 B.8 C.15 D.17
【答案】D
【解析】解: ,
又∵ ,∴ ∴ ,
∴ (当且仅当 时,取“=”)
故选:D
10.已知集合 ,则满足条件B⊆A的集合B的个数为
( )
A.2 B.3 C.4 D.8
【答案】C
【解析】
解:由 解得: . , 或 .则 ,
所以根据集合子集个数公式得满足条件B⊆A的集合B的个数为 .
故选:C.
11.已知不等式 的解集为 ,则不等式 的
解集为( )
A. B. 或C. D. 或
【答案】C
【解析】
由于不等式 的解集为 ,
则关于 的方程 的两根分别为 、 且满足 ,
由韦达定理得 ,解得 ,
所以,不等式 即为 ,
即 ,解得 .
因此,不等式 的解集是 .
故选:C.
12.若集合 ,则实数 的取值范围是 ( )
A. B.C. D.
【答案】D
【解析】
设
当 时, ,满足题意
当 时, 时二次函数
因为
所以 恒大于0,
所以 ,解得 .
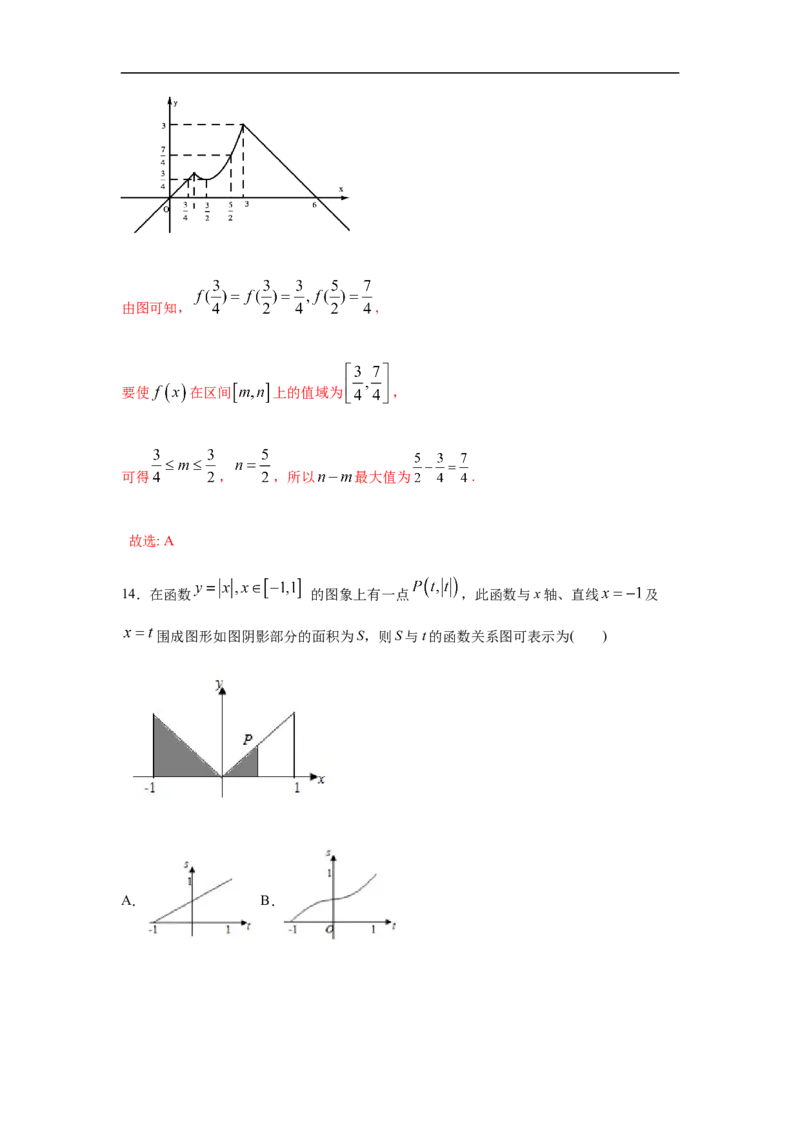
13.定义 ,若函数 ,且
在区间 上的值域为 ,则区间 长度的最大值为( )
A. B. C. D.
【答案】A
【解析】
画出分段函数 的图像,如下:由图可知, ,
要使 在区间 上的值域为 ,
可得 , ,所以 最大值为 .
故选: A
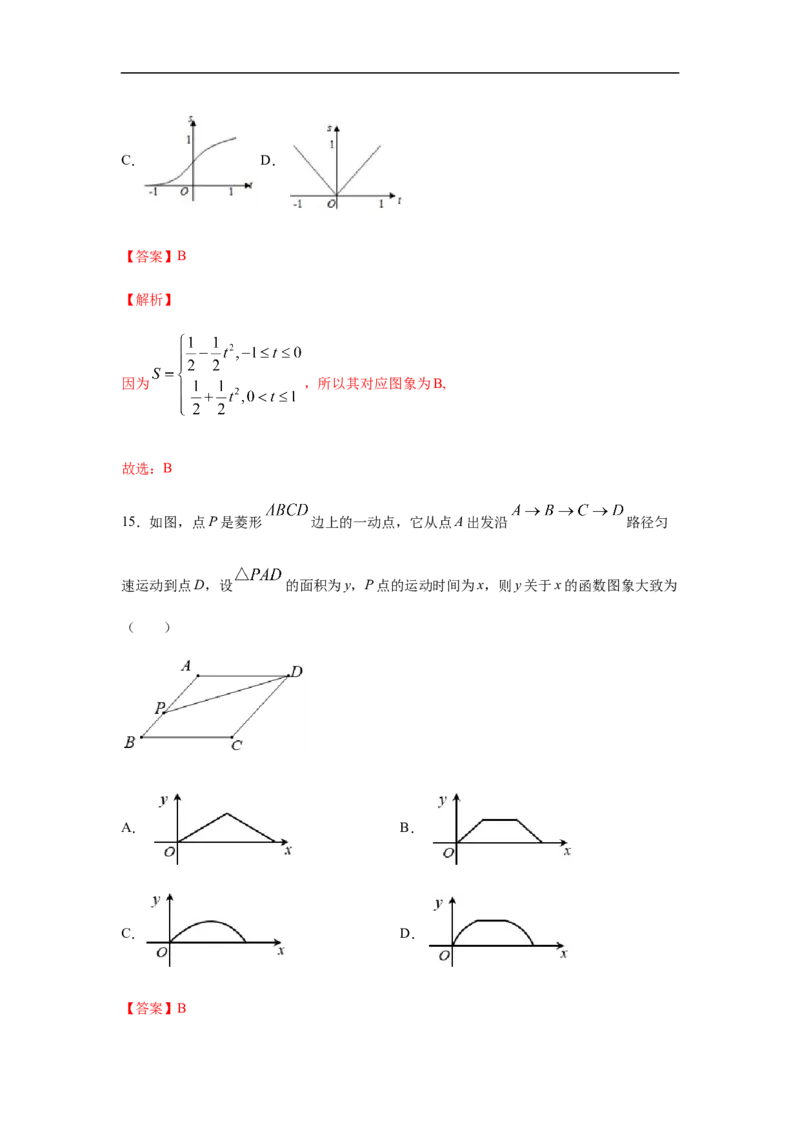
14.在函数 的图象上有一点 ,此函数与x轴、直线 及
围成图形如图阴影部分的面积为S,则S与t的函数关系图可表示为( )
A. B.C. D.
【答案】B
【解析】
因为 ,所以其对应图象为B,
故选:B
15.如图,点P是菱形 边上的一动点,它从点A出发沿 路径匀
速运动到点D,设 的面积为y,P点的运动时间为x,则y关于x的函数图象大致为
( )
A. B.
C. D.
【答案】B【解析】
当 时,
当 时, 线性增长, 的面积也线性增长;
当 时, 不变, 的面积不变;
当 时, 线性减小, 的面积也线性减小;
故选:B
16.设f(x)= ,若f(a)=f(a+1),则 =( )
A.2 B.4 C.6 D.8
【答案】C
【解析】
由察可知分段函数在两个区间内都是单调增函数,得0