专题36相关关系与线性回归模型及其应用（解析版）_E015高中全科试卷_数学试题_选修3_05.专项训练_专题36相关关系与线性回归模型及其应用

专题36 相关关系与线性回归模型及其应用 一、单选题 y x R2 1．（2020·四川宜宾·期末（文））两个变量 与 的回归模型中，有4个不同模型的相关指数 如下， 其中拟合效果最好的是（ ） R2 0.96 R2 0.81 R2 0.50 R2 0.25 A． B． C． D． 【答案】A 【解析】 y x R2 两个变量 与 的回归模型中，相关指数 越大，拟合效果越好，  0.960.810.500.25，  R2 0.96 拟合效果最好的是 ， 故选：A． 2．（2020·内蒙古赤峰·期末（文））某服装厂引进新技术，其生产服装的产量x（百件）与单位成本 y yˆ 100.3614.2x （元）满足回归直线方程 ，则以下说法正确的是（ ） 14.2 A．产量每增加100件，单位成本约下降 元 100.36 B．产量每减少100件，单位成本约上升 元 14.2 C．产量每增加100件，单位成本约上升 元 14.2 D．产量每减少100件，单位成本约下降 元 【答案】A 【解析】 b 14.20 14.2 表示产量每增加100件，单位成本约下降 元， 故选：A x,y D3,10 3．（2020·雅安市教育科学研究所期末（理））如图所示，5组数据 中去掉 后，下列说法错误的是( ) A．残差平方和变大 B．相关系数r变大 R2 C．相关指数 变大 D．解释变量x与预报变量y的相关性变强 【答案】A 【解析】 D(3,10) y x 由散点图知，去掉 后， 与 的线性相关加强，且为正相关， r R2 所以 变大， 变大，残差平方和变小． 故选A． x ,y ,x ,y , ,x ,y  n�2,x ,x , ,x 4．（2020·陕西富平·期末（文））在一组样本数据 1 1 2 2  n n （ 1 2  n不全 x,y (i1,2, ,n) y 0.4x1 相等）的散点图中，若所有样本点 i i  都在直线 上，则这组样本数据的样本相 关系数为（ ） A．1 B．0.4 C．0.5 D．1 【答案】D 【解析】 x,y (i1,2, ,n) y 0.4x1 因为所有样本点 i i  都在直线 上， 所以这组数据完全相关， 即说明这组数据完全正相关，相关系数为1. 故选：D 5．（2020·邵阳市第二中学其他（文））某种产品的广告费支出x与销售额 y （单位：万元）之间有如  表关系，y与x的线性回归方程为y 6.5x17.5，当广告支出5万元时，随机误差的效应（残差）为（ ）x 2 4 5 6 8 y 30 40 60 50 70 A．10 B．20 C．30 D．40 【答案】A 【解析】  因为y与x的线性回归方程为y 6.5x17.5，  所以当x5时，y 6.5517.550 由表格当广告支出5万元时，销售额为60万元，所以随机误差的效应（残差）为605010 故选A. x,y i 1,2,3,,n 6．（2020·福建三明·期末）对于一组具有线性相关关系的数据 i i ，根据最小二乘法 $ $ $ y bxa 求得回归直线方程为 ，则以下说法正确的是（ ） $ $ $ y bxa A．至少有一个样本点落在回归直线 上 B．预报变量 y 的值由解释变量x唯一确定 R2 C．相关指数 越小，说明该模型的拟合效果越好 D．在残差图中，残差点分布水平带状区域的宽度越窄，则回归方程的预报精确度越高 【答案】D 【解析】 x ,y  $ y  $ bx $ a 对于一组具有线性相关关系的数据 i i ，可能所有的样本点都不在回归直线 上，故A不正确； 预报变量 y 的值由解释变量x进行估计，所以B不正确； R2 相关系数 越小，残差的平方和越大，说明该模型的拟合效果越不好，所以C不正确； 在残差图中，残差点分布水平带状区域的宽度越窄，则回归方程的预报精确度越高，所以D正确. 故选：D. 7．（2020·陕西省商丹高新学校期中（文））某公司某件产品的定价x与销量y之间的数据统计表如下， y 6.5x17.5 根据数据，用最小二乘法得出y与x的线性回归直线方程为： ，则表格中n的值应为（） x 2 4 5 6 8 y 30 40 n 50 70 A．45 B．50 C．55 D．60 【答案】D 【解析】 190n 190n 6.5517.5,n60 由题得样本中心点（5， 5 ），所以 5 . 故答案为D 8．（2020·山西期末（文））对两个变量 y 和 x 进行回归分析，得到一组样本数据： x 1 ,y 1  、 x 2 ,y 2  、 x ,y  、 n n ，则下列说法中不正确的是（ ）   $ $ $ x,y A．由样本数据得到的回归方程y bxa必过样本中心 B．残差平方和越大的模型，拟合的效果越好 R2 R2 C．用相关指数 来刻画回归效果， 越大，说明模型的拟合效果越好 y x r 0.9362 y x D．若变量 和 之间的相关系数为 ，则变量 和 之间具有线性相关关系 【答案】B 【解析】   $ $ $ x,y 对于A选项，回归直线y bxa必过样本的中心 ，A选项正确； 对于B选项，残差平方和越大的模型，拟合的效果越差，B选项错误； R2 R2 对于C选项，用相关指数 来刻画回归效果， 越大，说明模型的拟合效果越好，C选项正确； y x r 0.9362 y x 对于D选项，若变量 和 之间的相关系数为 ，则变量 和 之间具有较强的线性相关关系， D选项正确. 故选：B. 二、多选题 9．（2020·山东淄博·期末）下列说法正确的是（ ）K2 k A．对于独立性检验，随机变量 的观测值 值越小，判定“两变量有关系”犯错误的概率越小 R2 B．在回归分析中，相关指数 越大，说明回归模型拟合的效果越好 ~ Bn,p Ex30 Dx20 n45 C．随机变量 ，若 ， ，则 y cekx z ln y z 0.3x4 ce4 k 0.3 D．以 拟合一组数据时，经 代换后的线性回归方程为 ，则 ， 【答案】BD K2 k 【解析】选项A：对于独立性检验，随机变量 的观测值 值越小，判定“两变量有关系”犯错误的概率越 大，故选项A错误； R2 选项B：在回归分析中，相关指数 越大，残差平方和越小，说明回归模型拟合的效果越好，故选项B 正确；  Exnp 30  选项C：随机变量 ~ Bn,p，若 Ex30 ， Dx20 ，则  Dxnp(1 p)20 ，解得： n90 ，故选项C错误； y cekx lny ln(cekx)lnclnekx lnckx z ln y 选项D：因为 ，所以 ，令 ， z lnckx z 0.3x4 lnc4 k 0.3 ce4 k 0.3 则 ，又 ，所以 ， ，则 ， ，故选项D正确. 故选：BD. 10．（2020·山东菏泽·期末）以下四个命题中，其中正确的是（ ） yabx b2 x1 y 3 a1 A．已知两个变量具有线性相关关系，其回归直线方程为 ，若 ， ， ，则 . B．两个随机变量相关性越强，则相关系数的绝对值越接近于0 y 0.2x12 y C．在回归直线方程 中，当变量x每增加一个单位时，则变量 平均增加0.2个单位； y cekx z ln y D．以模型 去拟合一组数据时，为了求出回归方程，设 ，将其变换后得到线性方程 z 0.3x4 ce4 k 0.3 ，则 ，【答案】ACD b2 x1 y 3 yabx 3a2 a1 【解析】对于选项A， ， ， 代入回归直线方程为 ，即 ，则 ，正确； 对于选项B，两个随机变量相关性越强，则相关系数的绝对值越接近于1，错误； y 0.2x12 对于选项C， 在回归直线方程 中，当变量x增加一个单位时，则变量  y 0.2(x1)120.2x120.2平均增加0.2个单位，正确； y cekx ln y lnckx z ln y z kxlnc z 0.3x4 对于选项D，对 两边取对数得 ，设 ，则 ，与 比 4lnc k 0.3 ce4 较得，则 ， ，即 ，正确. 故选：ACD. 11．（2020·陕西新城·西安中学其他（理））下列说法错误的是（ ）   x,y A．回归直线过样本点的中心 B．两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于1 C．在回归直线方程 y 0.2x0.8 中，当解释变量 x 每增加1个单位时，预报变量 y 平均增加 0.8 个单位 X Y K2 X Y D．对分类变量 与 ，随机变量 的观测值越大，则判断“ 与 有关系”的把握程度越小 【答案】CD 【解析】   x,y A．回归直线必过样本点的中心 ，故A正确； B．两个随机变量相关性越强，则相关系数的绝对值越接近1，故B正确； C y 0.2x0.8 x ．在线性回归方程 中，当 每增加1个单位时，预报量平均增加0.2个单位，故C错误； D X Y K2 k k X Y ．对分类变量 与 的随机变量 的观测值 来说， 越大，“ 与 有关系”可信程度越大，因 此不正确． 综上可知：有CD不正确． 故选：CD． 12．（2020·湖北期末）下列说法中正确的是（ ）A．将一组数据中的每一个数据都加上或减去同一个常数后，方差不变 yˆ 35x x yˆ B．设有一个线性回归方程 ，变量 增加1个单位时， 平均增加5个单位 x,y r |r| 0 x y C．设具有相关关系的两个变量 的相关系数为 ，则 越接近于 ， 和 之间的线性相关程度越强 22 K2 K2 D．在一个 列联表中，由计算得 的值，则 的值越大，判断两个变量间有关联的把握就越大 【答案】AD 【解析】 将一组数据中的每一个数据都加上或减去同一个常数后，方差不变，满足方差的性质，A正确； yˆ 35x yˆ 设有一个线性回归方程 ，变量x增加1个单位时， 平均减少5个单位；所以B不正确； |r| 设具有相关关系的两个变量x，y的相关系数为r，则 越接近于0，x和y之间的线性相关程度越弱，所 以C 不正确； K2 K2 在一个2×2列联表中，由计算得 的值，则 的值越大，判断两个变量间有关联的把握就越大，所以 D正确； 故选：AD． 三、填空题 13．（2020·海南枫叶国际学校期中）某设备的使用年限x与所支出的维修费用 y 的统计数据如下表： x 使用年限 （单位： 2 3 4 5 6 年） y 维修费用 （单位：万 1.5 4.5 5.5 6.5 7.0 元） 根据上表可得回归直线方程为 y 1.3xa ，据此模型预测，若使用年限为14年，估计维修费约为 __________万元． 【答案】18 【解析】 23456 1.54.55.56.57.0 x  4,y  5 5 5 ，4,5 aˆ 51.340.2 y 1.3x0.2 则中心点为 ，代入回归直线方程可得 ， . x14 y 1.3140.218 当 时， （万元）， 即估计使用14年时，维修费用是18万元. 故答案为：18. 14．（2020·吉林高二期末（文））下列关于回归分析的说法中错误的序号为_______ （1）残差图中残差点所在的水平带状区域越宽，则回归方程的预报精确度越高．   x,y （2）回归直线一定过样本中心点 ． （3）两个模型中残差平方和越小的模型拟合的效果越好． R2 （4）甲、乙两个模型的 分别约为0.88和0.80，则模型乙的拟合效果更好． 【答案】（1）（4） 【解析】 对于（1），残差图中残差点所在的水平带状区域越窄，则回归方程的预报精确度越高，∴（1）错误；   x,y 对于（2），回归直线一定过样本中心点 ，正确； 对于（3），两个模型中残差平方和越小的模型拟合的效果越好，正确； R2 对于（4），甲、乙两个模型的 分别约为0.88和0.80，则模型甲的拟合效果更好，∴（4）错误； 综上，错误的命题是（1）、（4）共2个. 故答案为：（1）（4）. $ $ $ y bxa 15．（2020·黑龙江高二期末（文））下列命题中，正确的命题有_____.①回归直线 恒过样本点   x,y 中心 ，且至少过一个样本点；②用相关指数R2来刻画回归效果，表示预报变量对解释变量变化的贡 R2 献率， 越接近于1说明模型的拟合效果越好；③残差图中残差点比较均匀的落在水平的带状区域中，说 明选用的模型比较合适；④两个模型中残差平方和越大的模型的拟合效果越好. 【答案】②③ 【解析】  $ $ $ x,y ①回归直线y bxa恒过样本点中心 ， 但不一定过样本点，故错误； R2 R2 ②用相关指数 来刻画回归效果.在线性回归模型中，表示预报变量对解释变量变化的贡献率， 越接 近于1说明模型的拟合效果越好，故正确； ③残差图中残差点比较均匀的落在水平的带状区域中，说明选用的模型比较合适；正确. ④两个模型中残差平方和越小的模型的拟合效果越好，故错误. 故答案为：②③ 16．（2018·北京全国·高二单元测试（理））关于x与 y ，有如下数据有如下的两个模型：(1) yˆ 6.5x17.5 yˆ 7x17 R2 ；(2) .通过残差分析发现第（1）个线性模型比第（2）个拟合效果好，则 1 R2 Q Q R,Q ________ 2 ， 1______ 2（用大于，小于号填空， 是相关指数和残差平方和） x 2 4 5 6 8 y 30 40 60 50 70 【答案】  【解析】 R2 由相关指数 的的性质可得， R2 R2  R2 越大模型的拟合效果越好，所以 1 2 , 由残差的性质可得， 残差平方和越小模型的拟合效果越好， Q Q , 所以 1 2，故答案为 . 四、解答题 17．（2020·全国高考真题（理））某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加. 为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方 法抽取20个作为样区，调查得到样本数据(x，y)(i=1，2，…，20)，其中x和y分别表示第i个样区的植物 i i i i 20 20 20 x 60 y 1200 （x x)2 80 覆盖面积(单位：公顷)和这种野生动物的数量，并计算得 i ， i ， i ， i1 i1 i120 20 （y  y)2 9000 （x x（) y  y)800 i ， i i . i1 i1 （1）求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平 均数乘以地块数）； （2）求样本(x，y)(i=1，2，…，20)的相关系数（精确到0.01）； i i （3）根据现有统计资料，各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动 物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由. n （x x（) y  y) i i i1 附：相关系数r= n n ， ≈1.414. （x x)2（y  y)2 i i i1 i1 12000 0.94 【答案】（1） ；（2） ；（3）详见解析 【解析】 1 20 1 y  120060 （1）样区野生动物平均数为20 i 20 ， i1 2006012000 地块数为200，该地区这种野生动物的估计值为 (x ,y ) （2）样本 i i (i=1，2，…，20)的相关系数为 20 (x x)(y  y) i i 800 2 2 r  i1   0.94 20 20 809000 3 (x x)2(y  y)2 i i i1 i1 （3）由（2）知各样区的这种野生动物的数量与植物覆盖面积有很强的正相关性， 由于各地块间植物覆盖面积差异很大，从俄各地块间这种野生动物的数量差异很大， 采用分层抽样的方法较好地保持了样本结构与总体结构得以执行，提高了样本的代表性， 从而可以获得该地区这种野生动物数量更准确的估计. 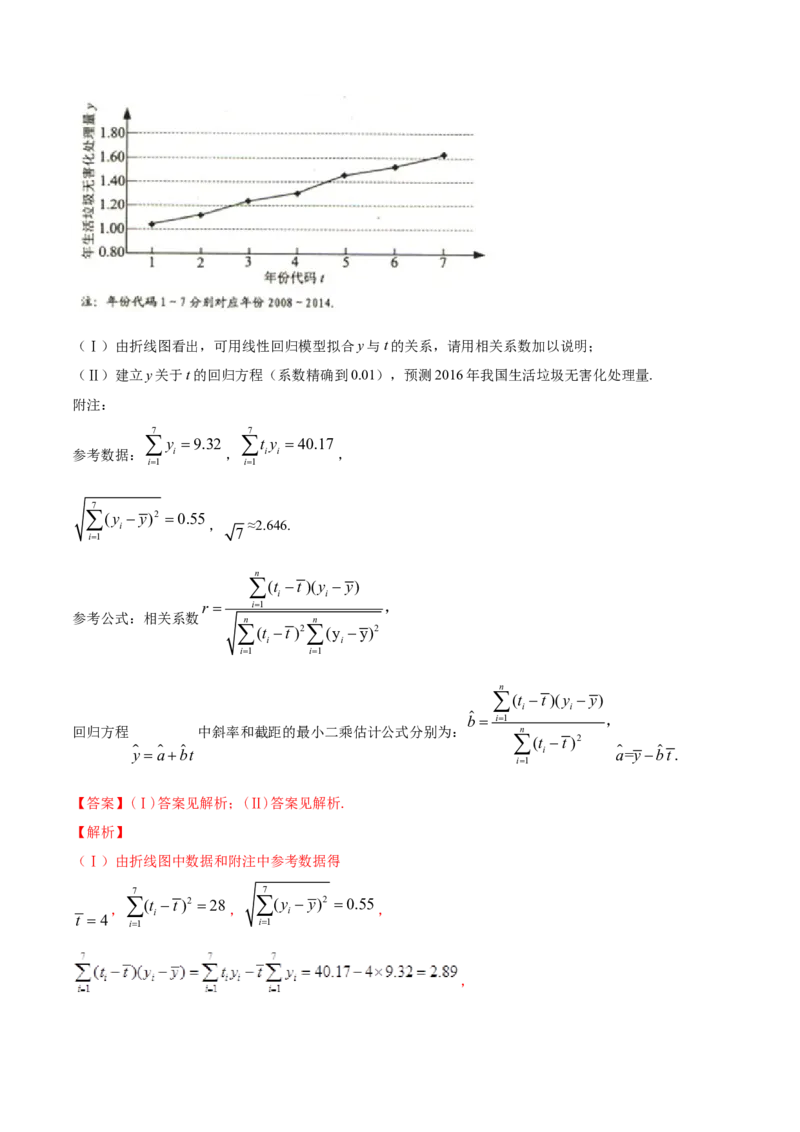18．（2016·全国高考真题（文））下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的 折线图.（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明； （Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量. 附注： 7 7 y 9.32 t y 40.17 参考数据： i ， i i ， i1 i1 7 (y  y)2 0.55 i ， ≈2.646. 7 i1 n (t t )(y  y) i i r  i1 ， 参考公式：相关系数 n n (t t )2(y y)2 i i i1 i1 n (t t )(y  y) i i b  i1 ， 回归方程 中斜率和截距的最小二乘估计公式分别为： n (t t )2 y abt i a=ybt. i1 【答案】(Ⅰ)答案见解析；(Ⅱ)答案见解析. 【解析】 （Ⅰ）由折线图中数据和附注中参考数据得 7 7 (t t )2 28 (y  y)2 0.55 ， i ， i ， t 4 i1 i1 ，. 因为 与 的相关系数近似为0.99，说明 与 的线性相关相当高，从而可以用线性回归模型拟合 与 的 关系. 7 (t t )(y  y) i i 2.89 b ˆ  i1  0.103 （Ⅱ）由 9.32 及（Ⅰ）得 7 28 ， y  1.331 (t t )2 i 7 i1 ˆ aˆ  ybt 1.3310.10340.92 . 所以， 关于 的回归方程为： . 将2016年对应的 代入回归方程得： . 所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨. 19. （2020·吉林洮北·白城一中期末（理））为了解某地区某种产品的年产量x（单位：吨）对价格 y （单 位：千元/吨）和利润z 的影响，对近五年该农产品的年产量和价格统计如下表： ˆ y x yˆ bxaˆ （1）求 关于 的线性回归方程 ； （2）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z 取到 最大值？（保留两位小数） n n (x x)(y  y) x y nxy i i i i b ˆ  i1  i1 参考公式： n n ，^ ^ (x x)2 x2 nx2  y x i i a b i1 i1 yˆ 8.691.23x x2.72 z 【答案】(1) (2) ，年利润 最大 【解析】 x 3 y 5 （1） ， ，5 5 5 5 5 x 15 y 25 x y 62.7 x2 55 x2 55 i ， i ， i i ， ， i ， i1 i1 i1 i1 i1 ^ ^ 1.23 8.69 解得：b ，a ， yˆ 8.691.23x 所以： ， z  x8.691.23x2x1.23x2 6.69x （2）年利润 所以x2.72，年利润z 最大. 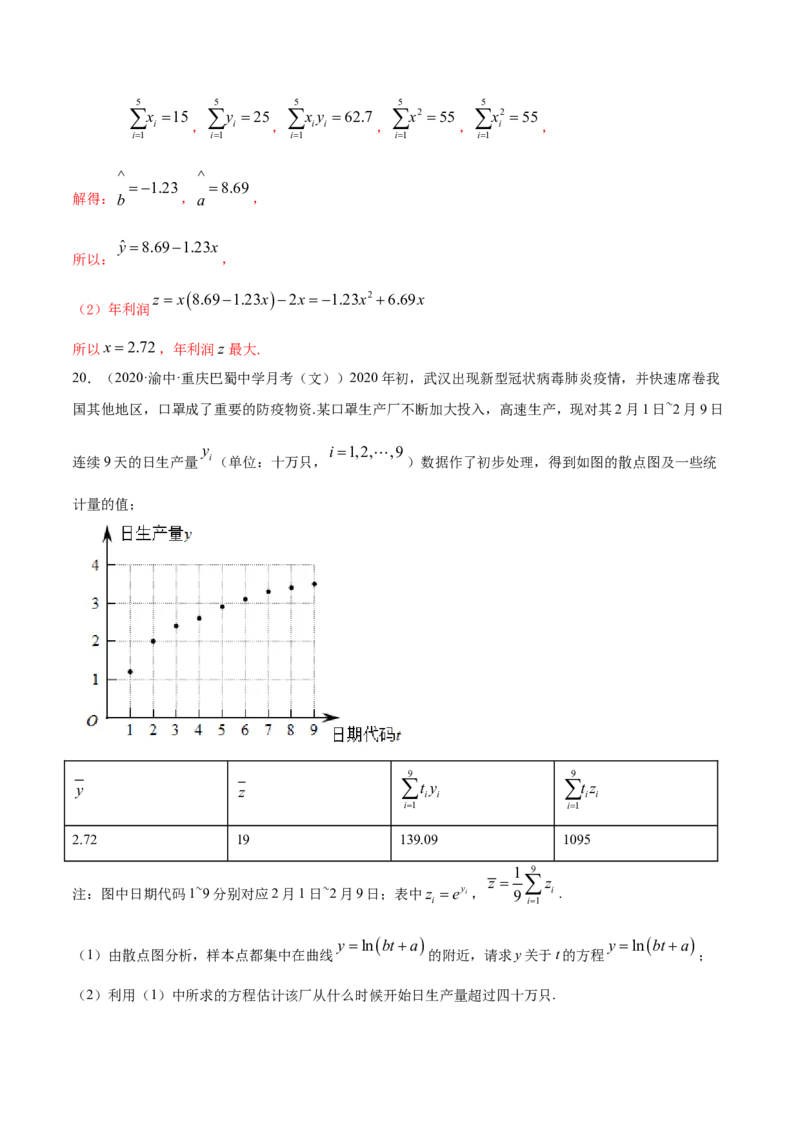20．（2020·渝中·重庆巴蜀中学月考（文））2020年初，武汉出现新型冠状病毒肺炎疫情，并快速席卷我 国其他地区，口罩成了重要的防疫物资.某口罩生产厂不断加大投入，高速生产，现对其2月1日~2月9日 y i 1,2, ,9 连续9天的日生产量 i（单位：十万只，  ）数据作了初步处理，得到如图的散点图及一些统 计量的值； 9 9 y z t y t z i i i i i1 i1 2.72 19 139.09 1095 1 9 z  z 注：图中日期代码1~9分别对应2月1日~2月9日；表中z ey i ， 9 i . i i1 y lnbta y lnbta （1）由散点图分析，样本点都集中在曲线 的附近，请求y关于t的方程 ； （2）利用（1）中所求的方程估计该厂从什么时候开始日生产量超过四十万只.n n v v uv nv i i i i  ˆ  i1  i1 参考公式：回归直线方程是 时， n n ， . 2 u2 n2 v ˆ ˆ i i ˆ v  ˆ  i1 i1 e4 54.6 参考数据： . y ln4t1 【答案】（1） ；（2）2月14日开始日生产量超过四十万只. 【解析】 y lnbta z ey bta （1）∵ ，∴ . 9 t2 285 t 5， i ， i1 9 t z 9t z i i 10959519 b i1  4 ∴ 9 285952 ， t2 9t 2 i i1 a z bt 19451 ∴ . y ln4t1 ∴ . e4 1 （2）令ln4t14，解得 t  4 13.9 ， ∴t14，即该厂从2月14日开始日生产量超过四十万只. 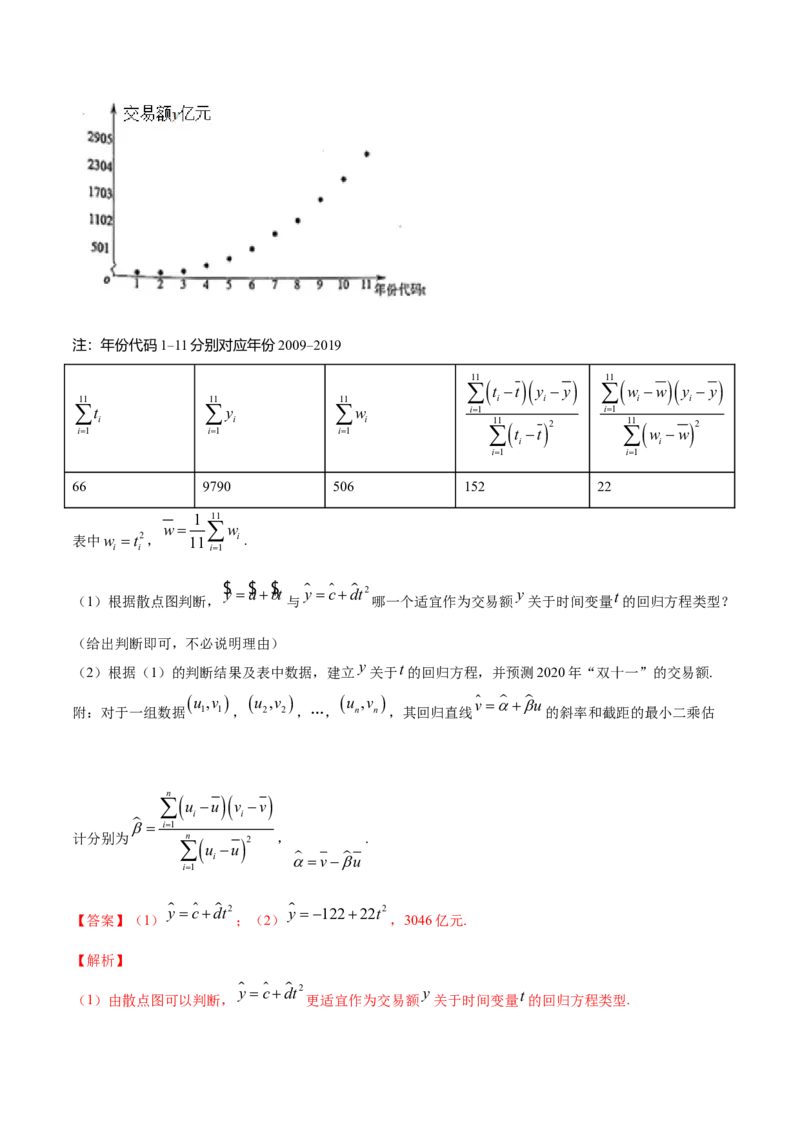21．（2020·福建三明·期末）“双十一”是阿里巴巴从2009年起举办的一个全民购物狂欢活动.11年来， 天猫“双十一”交易额年年创新高，为预测2020年“双十一”的交易额，收集了历年天猫“双十一”活动 y 的交易额 （亿元），对数据作了初步处理，得到下面的散点图及一些统计量的值.注：年份代码1-11分别对应年份2009-2019 11 11  t t  y  y   w w  y  y  11 11 11 i i i i t y w i1 i1 i1 i i1 i i1 i  11  t t 2  11  w w 2 i i i1 i1 66 9790 506 152 22 1 11 w w 表中w t2， 11 i . i i i1 $ y  $ a $ bt y cdt2 y t （1）根据散点图判断， 与 哪一个适宜作为交易额 关于时间变量 的回归方程类型？ （给出判断即可，不必说明理由） （2）根据（1）的判断结果及表中数据，建立 y 关于t的回归方程，并预测2020年“双十一”的交易额. u ,v  u ,v  u ,v  v u 附：对于一组数据 1 1 ， 2 2 ，…， n n ，其回归直线 的斜率和截距的最小二乘估 n  u u  v v  i i   i1 计分别为  n  u u 2 ， . i  vu i1 y cdt2 y 12222t2 【答案】（1） ；（2） ，3046亿元. 【解析】 y cdt2 y t （1）由散点图可以判断， 更适宜作为交易额 关于时间变量 的回归方程类型.wt2 y w （2）令 ，先建立 关于 的线性回归方程，由于 11  w w  y  y  i i d  i1 22  11  w w 2 ， y  1  11 y  9790 890 ， i 11 i 11 i1 i1 1 11 506 w w  46 11 i 11 ， i1 c  ydw8902246122 所以 ， y w y 12222w 所以 关于 的线性回归方程为 ， y t y 12222t2 因此 关于 的回归方程为 ， t 12 y 12222122 3046 令 得 ， 即可预测2020年“双十一”的交易额为3046亿元. 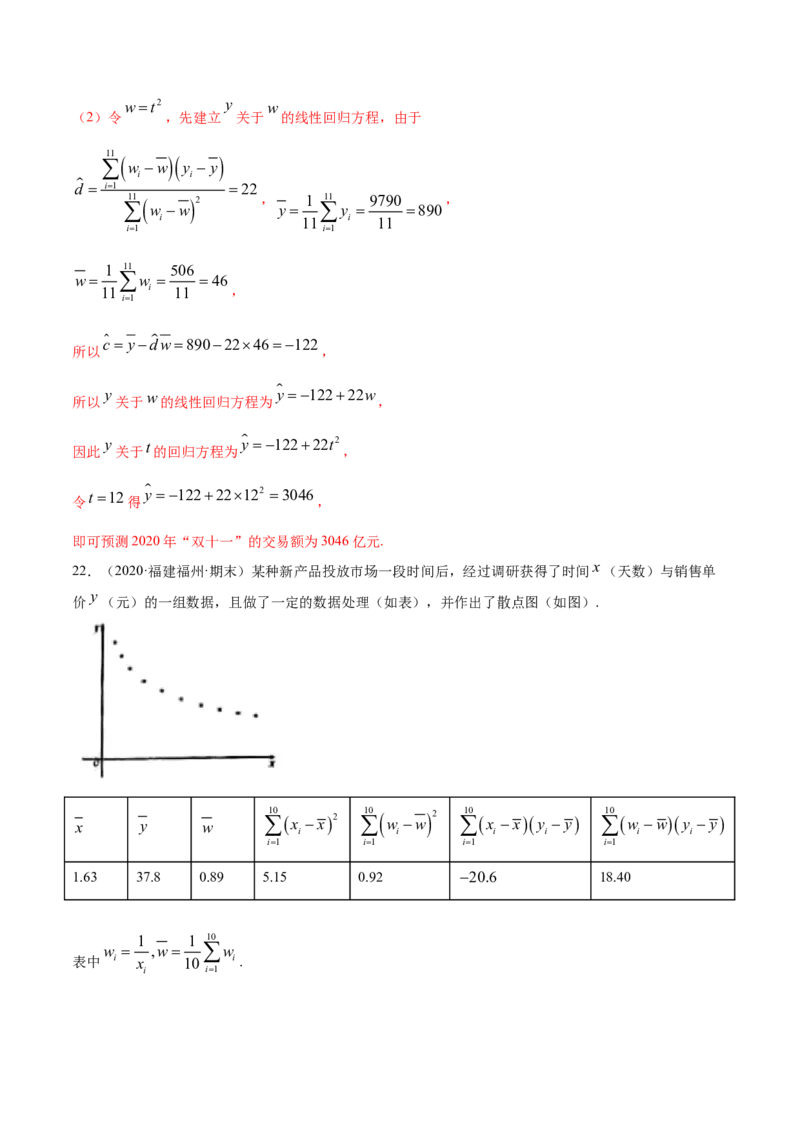x 22．（2020·福建福州·期末）某种新产品投放市场一段时间后，经过调研获得了时间 （天数）与销售单 y 价 （元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）. x y w  10 x x2  10  w w 2  10 x xy  y  10 w wy  y i i i i i i i1 i1 i1 i1 1.63 37.8 0.89 5.15 0.92 20.6 18.40 1 1 10 w  ,w w 表中 i x 10 i . i i1ˆ d yˆ cˆ （1）根据散点图判断，yˆ aˆb ˆ x与 x 哪一个更适合作价格y关于时间x的回归方程类型？（不 必说明理由） （2）根据判断结果和表中数据，建立 y 关于x的回归方程. 100 g(x) 120  xN* （3）若该产品的日销售量g(x)（件）与时间x的函数关系为 x ，求该产品投 放市场第几天的销售额最高？最高为多少元？ u ,v ,u ,v ,u ,v ,u ,v  vu 附：对于一组数据 1 1 2 2 3 3 n n ，其回归直线 的斜率和截距的最小二乘 n  v v  u u  i i ˆ ˆ  i1 ,aˆ vu 法估计分别为  n  u u 2 . i i1 ˆ d 20 yˆ cˆ yˆ 20 【答案】（1） x ，（2） x ，（3）该产品投放市场第10天的销售额最高，最高为 2420元. 【解析】 ˆ d yˆ cˆ （1）依据散点图，可知图象所表示得函数接近反比例函数，故 x 更适合作价格y关于时间x的回 归方程类型； 1  （2）令w x ，先建立y关于w的线性回归方程， 18.40 ˆ d  20 由于 0.92 ，所以cˆ37.8200.8920， y w yˆ 2020w 所以 关于 的线性方程为 ， 20 yˆ 20 所以y关于x的线性回归方程为 x .20 100 20 10 1 h(x) g(x)(20 ) ( 120)(20 ) 200( 12)( 1) （3）日销售额 x x x x x 1 1 2000[(  )2 1.21] x 10 x10 h(x) 2420 所以 时， 取得最大值 元.