文档内容
专题 4.1 指数
1 指数运算
(1) n次方根与分数指数幂
一般地,如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N∗.
式子√n a叫做根式,这里n叫做根指数,a叫做被开方数.
负数没有偶次方根;0的任何次方根都是0.
注 意 : (1) (2) 当 是 奇 数 时 , , 当 是 偶 数 时 ,
(√n a) n=a n √n an=a n
√n an=|a|={ a,a≥0
.
−a,a<0
(2) 正数的正分数指数幂的意义
m
① 正数的正分数指数幂的意义,规定:
an =√n am (a>0,m,n∈N∗,且n>1)
巧记“子内母外”(根号内的m作分子,根号外的n作为分母)
m
− 1 1
② 正数的正分数指数幂的意义:a n = = (a>0,m,n∈N∗,且n>1)
m √n am
an
③ 0的正分数指数幂等于0,0的负分数指数幂没有意义.
(3) 实数指数幂的运算性质
① ;
as∙ar=ar+s (a>0,r,s∈R)
② (as) r =ars (a>0,r,s∈R) ;
③ .
(ab) r=arbr (a>0,r∈R)
一、单选题a
1.已知 , , ,则a,b,c的大小关系为( )
A. B.
C. D.【答案】B
【解析根据题意,因为 , ,所以 .故选:B.
2.若代数式 有意义,则 ( )
A. B. C. D.
【答案】B
【解析】由 有意义,得 解得 .
所以
所以
.
故选:B.
3. 可以化简成( )
A. B. C. D.
【答案】B
【解析】解: ,
故选:B.
4.函数 的图像可能是( ).
A. B.C. D.
【答案】D
【解析】当 时,∴ ,所以排除B,
当 时,∴ ,所以排除C,故选D.
5.已知函数 ,则 ( )
A. B. C. D.
【答案】B
【解析】由题设, ,
所以 .
故选:B.
6.化简 得
A. B. C. D.
【答案】A
【解析】依题意,原式 .
故选:A
7.化简 (a>0)等于( )
A.6a B.-aC.-9a D.9a2
【答案】C
【解析】 故选:C
8.有下列四个式子:
① ;
② ;
③ ;
④
其中正确的个数是( )
A. B. C. D.
【答案】A
【解析】① 正确;② ,② 错误;③
,③ 错误;④ ,若 ,则
,若 ,则 ,故④ 错误.
故选:A
9.化简 的结果为( )
A. B.
C. D.
【答案】B
【解析】因为 ,
,,
,
,
所以原式= 故选:B
10.已知函数 ,则不等式 的解集为( )
A. B. C. D.
【答案】D
【解析】:当 时, ,因为 ,所以 ,
故当 时,不等式无解,
当 时, ,
令 ,得 ,解得 .
故选:D.
11.已知函数 若 ,则实数 的值是( )
A.1 B.2 C.3 D.4
【答案】B
【解析】由题意可知, , ,
又因为 ,所以 ,解得 .
故选:B.
12.定义在实数集 上的奇函数 恒满足 ,且 时,,则 ( )
A. B. C.1 D.
【答案】B
【解析】解: 奇函数 恒满足 ,
,即 ,则 ,即 ,
即 是周期为4的周期函数,
所以 ,
故选:B.
13.已知 ,求 的值为
A.2 B.8 C.10 D.14
【答案】D
【解析】: ,
两边同时3次方得: ,
化简得: ,
又 ,
,
故选: .
14.
A. B. C. D.
【答案】A
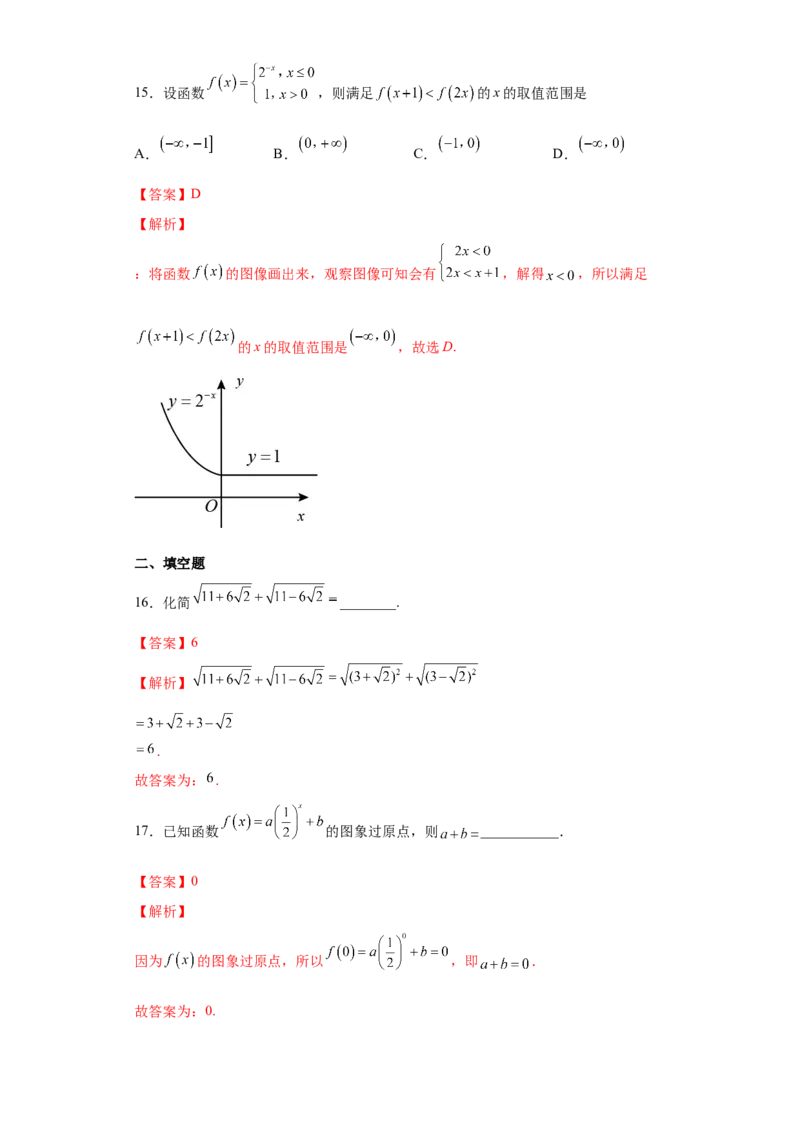
【解析】由题意可知 ,故选A.15.设函数 ,则满足 的x的取值范围是
A. B. C. D.
【答案】D
【解析】
:将函数 的图像画出来,观察图像可知会有 ,解得 ,所以满足
的x的取值范围是 ,故选D.
二、填空题
16.化简 ________.
【答案】6
【解析】
.
故答案为: .
17.已知函数 的图象过原点,则 ___________.
【答案】0
【解析】
因为 的图象过原点,所以 ,即 .
故答案为:0.18.求值 _______.
【答案】4
【解析】 .
故答案为:4
19.已知 ,,则 的值为______.
【答案】47
【解析】由 ,得 ,即 ,
所以 ,则 .
故答案为: .
20.化简 ___________.
【答案】 ##1.6
【解析】
故答案为:
21.已知 , ,则 ______.
【答案】 ##
【解析】因为 , ,
所以 .
故答案为:22.若 , ,则 的值为______.
【答案】
【解析】将 代入 ,得 ,
所以 .
故答案为: .
三、解答题
23.(1)求值: ;
(2)已知 ,求值: .
【答案】(1)81;(2)6.
【解析】(1)原式 ;
(2)由 ,而 ,
则 ,故 .
24.已知 , ,求 的值.
【答案】
【解析】化简 ,因为 ,,所以 .
25.计算或化简下列各式:
(1)(a-2)·(-4a-1)÷(12a-4)(a>0);
(2) -10( -2)-1+( )0.
【答案】(1)- a;(2)- .
【解析】(1)原式
(2)原式
= +10 -10 -20+1=- .
26.(1)计算: ;
(2)已知 ,求 .
【答案】(1)3;(2) .
【解析】(1)原式 ,
.
(2)由于 ,所以 , ,所以 .