文档内容
专题 4.2 指数函数
1、指数函数的概念:一般地,函数 叫做指数函数,其中x是自变量,函数
的定义域为R.
注意:指数函数的底数的取值范围,底数不能是负数、零和1.即 a>0且a≠1
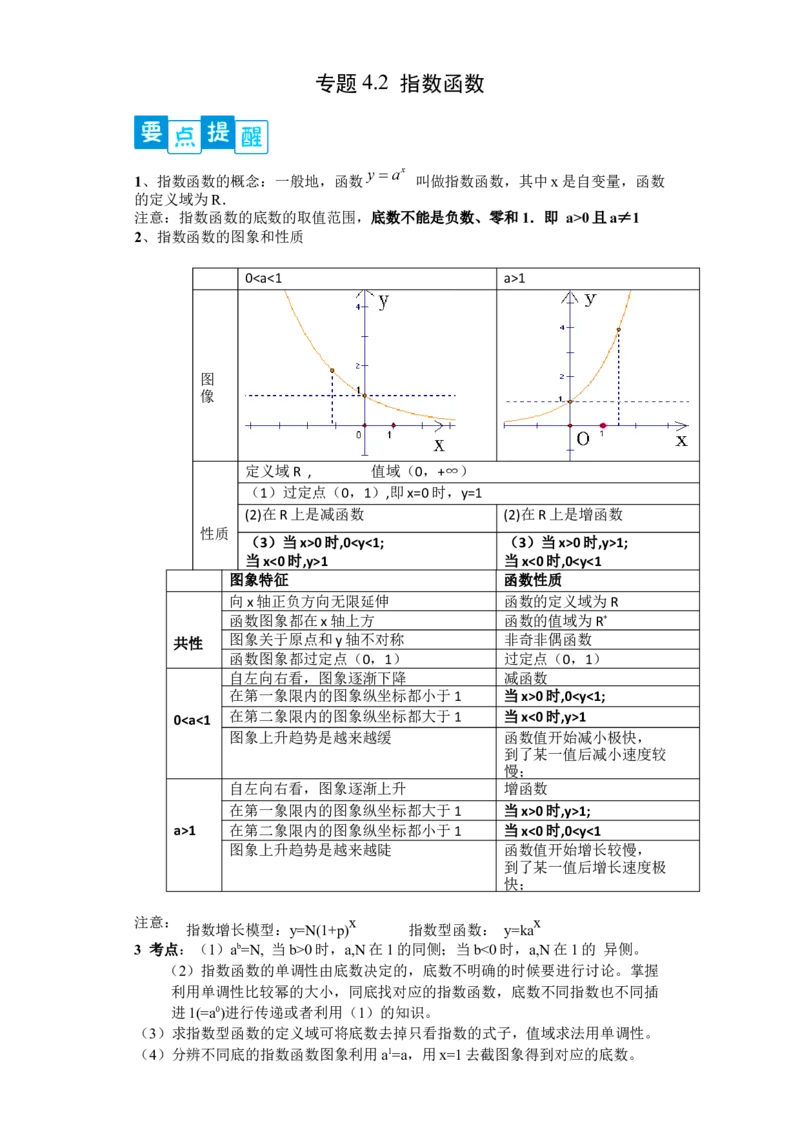
2、指数函数的图象和性质
01
图
像
定义域R , 值域(0,+∞)
(1)过定点(0,1),即x=0时,y=1
(2)在R上是减函数 (2)在R上是增函数
性质
(3)当x>0时,00时,y>1;
当x<0时,y>1 当x<0时,00时,01
图象上升趋势是越来越缓 函数值开始减小极快,
到了某一值后减小速度较
慢;
自左向右看,图象逐渐上升 增函数
在第一象限内的图象纵坐标都大于1 当x>0时,y>1;
a>1 在第二象限内的图象纵坐标都小于1 当x<0时,00时,a,N在1的同侧;当b<0时,a,N在1的 异侧。
(2)指数函数的单调性由底数决定的,底数不明确的时候要进行讨论。掌握
利用单调性比较幂的大小,同底找对应的指数函数,底数不同指数也不同插
进1(=a0)进行传递或者利用(1)的知识。
(3)求指数型函数的定义域可将底数去掉只看指数的式子,值域求法用单调性。
(4)分辨不同底的指数函数图象利用a1=a,用x=1去截图象得到对应的底数。一、单选题
1.若函数 是指数函数,则 等于( )
A. 或 B.
C. D.
2.函数 ,( 且 )的图象必经过一个定点,则这个定点的坐标是
( )
A. B. C. D.
3.若函数 为 上的奇函数,则实数 的值为( )
A. B. C.1 D.2
4.已知 是定义在R上的奇函数,且 ,当 时, ,则
( )
A.2 B.-2 C.0 D.
5.已知f(x)= ,则f(4)+f(-4)=( )
A.63 B.83 C.86 D.91
6.函数 的图象大致为( )A. B
C. D
7.若 ,则a、b、c的大小关系是( )
A. B. C. D.
8.设函数 对任意的 ,都有 , ,且当
时, ,则 ( )
A. B. C. D.
9. 是定义域为 的函数,且 为奇函数, 为偶函数,则 的
值是( )
A. B. C. D.
10.若 ,则下列关系式一定成立的是( )
A. B.
C. D.
11.已知函数 是定义在 上的偶函数,当 时, ,则不等式
的解集为( )A. B.
C. D.
12.已知函数 在 上单调递增,则实数 的取值范围是
( )
A. B.
C. D.
13.函数 的单调递增区间为( )
A. B. C. D.
14.已知函数 , ,则函数 的值域为( ).
A. B. C. D.
15.函数 , ,若对 ,都存在 ,使
成立,则m的取值范围是( )
A. B. C. D.
二、多选题
16.已知函数 ,则( )
A. 的值域为R B. 是R上的增函数
C. 是R上的奇函数 D. 有最大值
17.已知函数 ,则下列结论正确的有( )A. 的图象关于坐标原点对称 B. 的图象关于 轴对称
C. 的最大值为1 D. 在定义域上单调递减
18.下列结论中,正确的是( )
A.函数 是指数函数
B.函数 的单调增区间是
C.若 则
D.函数 的图像必过定点
19.已知函数 ,则下列结论正确的是( )
A.函数 的定义域为R
B.函数 的值域为
C.函数 的图象关于y轴对称
D.函数 在R上为增函数
20.已知 , 都是定义在 上的函数,其中 是奇函数, 为偶函数,
且 ,则下列说法正确的是( )
A. 为偶函数
B.
C. 为定值
D.
三、填空题
21.已知函数 ,若 ,则实数 的取值范围是___.22.已知函数 为定义在R上的奇函数,则 ____.
23.已知 是定义在 上的奇函数,且 ,当 时, ,
则 ___________.
24.设不等式 对于任意的 恒成立,则实数 的取值范围
是_______.
四、解答题
25.已知定义在 上的奇函数 .在 时, .
(1)试求 的表达式;
(2)若对于 上的每一个值,不等式 恒成立,求实数 的取值范
围.
26.已知函数 是定义域为 的奇函数.
(1)若集合 , ,求 ;
(2)设 ,且 在 上的最小值为-7,求实数 的值.
27.已知定义在 上的奇函数 ,当 时,函数解析式为
.
(1)求a的值,并求出 在 上的解析式;
(2)若对任意的 ,总有 ,求实数t的取值范围.28.已知函数 .
(1)求 的值;
(2)求函数 的值域;
(3)若 ,且对任意的 、 ,都有 ,
求实数 的取值范围.
29.设函数 ( 且 )是定义域为 的奇函数.
(1)求实数k的值;
(2)若 , ,且当 时, 恒成立,求实
数m的取值范围.