文档内容
专题 8.1 成对数据的统计相关性
姓名: 班级:
重点 变量的相关关系。
难点 样本相关系数。
例1-1.有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;②平均日学习时间和平均学
习成绩;③某人每日吸烟量和身体健康情况;④圆的半径与面积;⑤汽车的重量和每千米耗油量。其中两
个变量成正相关的是( )。
A、①③
B、②④
C、②⑤
D、④⑤
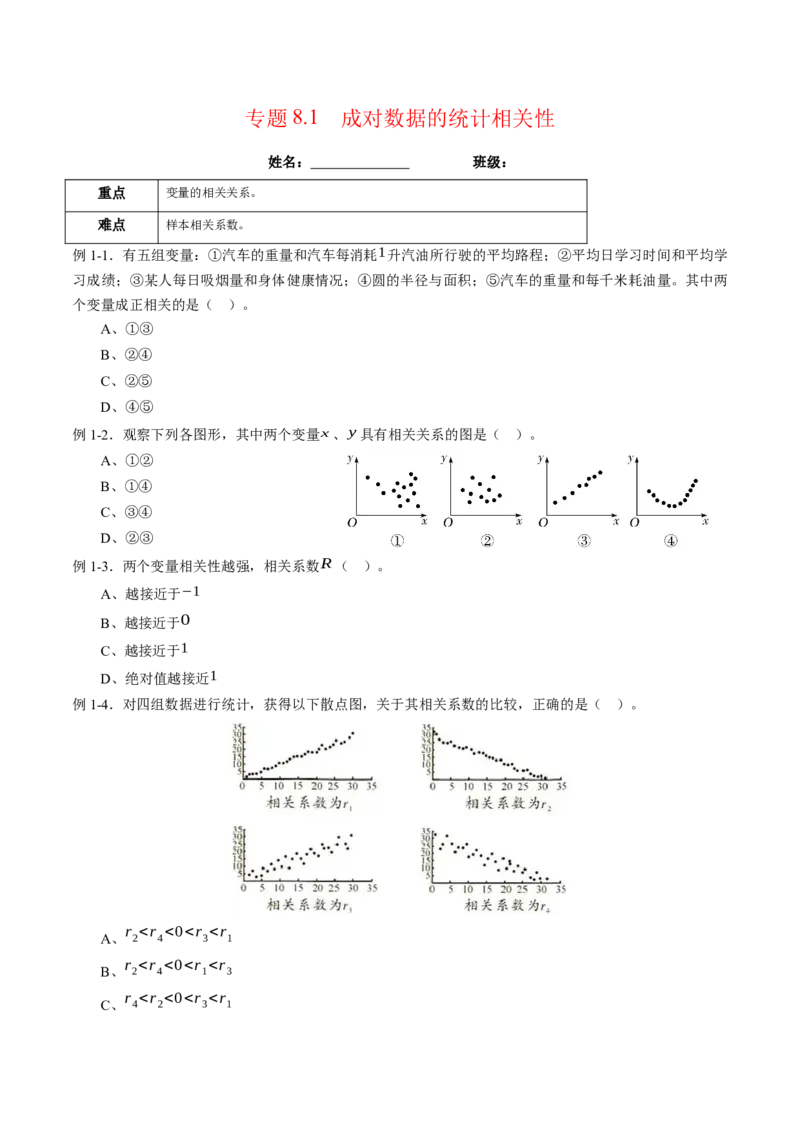
例1-2.观察下列各图形,其中两个变量x、y具有相关关系的图是( )。
A、①②
B、①④
C、③④
D、②③
例1-3.两个变量相关性越强,相关系数R( )。
A、越接近于−1
B、越接近于0
C、越接近于1
D、绝对值越接近1
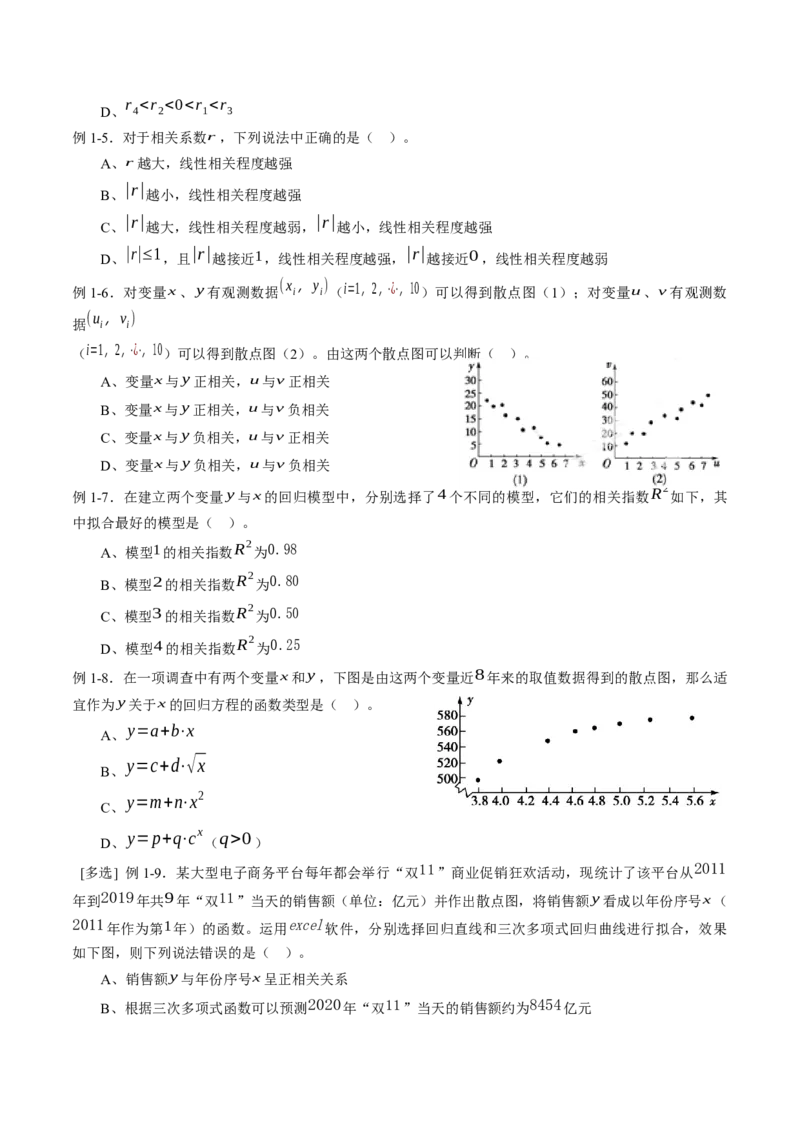
例1-4.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )。
r 0
D、 ( )
[多选] 例1-9.某大型电子商务平台每年都会举行“双11”商业促销狂欢活动,现统计了该平台从 2011
年到 2019 年共9年“双11”当天的销售额(单位:亿元)并作出散点图,将销售额y看成以年份序号x(
2011 年作为第1年)的函数。运用 excel 软件,分别选择回归直线和三次多项式回归曲线进行拟合,效果
如下图,则下列说法错误的是( )。
A、销售额y与年份序号x呈正相关关系
B、根据三次多项式函数可以预测 2020 年“双11”当天的销售额约为 8454 亿元C、销售额y与年份序号x线性相关不显著
D、三次多项式回归曲线的拟合效果好于回归直线的拟合效果
例1-10.相关指数R2
= 。
例1-11.某地区在“精准扶贫”工作中切实贯彻习近平总书记提出的“因地制宜”的指导思想,扶贫工作
小组经过多方调研,综合该地区的气候、地质、地理位置等特点,决定向当地农户推行某类景观树苗种植。
经考察已知树苗经引种成活后再经过1年的生长即可作为景观树在市场上出售,但每株售价y(单位:百
元)受其树干的直径x(单位:cm)影响,扶贫工作小组对一批已出售的景观树的相关数据进行统计,得
到结果如下表:
直径x 10 15 20 25 30
单株售价y 4 8 10 16 27
根据上述数据,判断是否可用线性回归模型拟合y与x的关系?并用相关系数r加以说明。
n n
∑(x −x)(y −y) ∑x⋅y −n⋅x⋅y
i i i i
r= i=1 = i=1
√ n n √ n √ n
∑(x −x)2⋅∑(y −y)2 ∑x2−n⋅x2⋅ ∑ y2−n⋅y2
i i i i
附:相关系数 i=1 i=1 i=1 i=1 ,
5 5
∑(x
i
−x)2=250 ∑(y
i
−y)2=320
|r|>0.75
i=1 ,i=1 ,一般认为, 为高度线性相关。
例1-12.根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图,如图所示。
依据数据的散点图可以看出,可用线性回归模型拟合y与x的关系,请计算相关系数r并加以说明
(若r>0.75
,则线性相关程度很高,可用线性回归模型拟合)。
n n
∑(x −x)(y −y) ∑x⋅y −n⋅x⋅y
i i i i
r= i=1 = i=1
√ n n √ n √ n
∑(x −x)2⋅∑(y −y)2 ∑x2−n⋅x2⋅ ∑ y2−n⋅y2
i i i i
附:相关系数公式 i=1 i=1 i=1 i=1 。