文档内容
必修第一册
本卷满分150分,考试时间120分钟。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一个选项是符合题目要求的.
1.设全集 ,集合 , ,则
( )
A. B. C. D.
【来源】山西省太原市太原师范学院附属中学、师苑中学2021-2022学年高一下学期开学
分班数学试题
【答案】D
【解析】由于 故集合
或 故集合 故选:D
2.已知“ ”是“ ”的充分不必要条件,则k的取值范围为( )
A. B. C. D.
【来源】甘肃省会宁县第一中学2021-2022学年高一上学期期末考试数学试题
【答案】C
【解析】因为 ,所以 或 ,
所以解集为 ,
又因为“ ”是“ ”的充分不必要条件,
所以 是 的真子集,所以 ,故选:C.
3.若不等式 对任意实数x均成立,则实数a的取值范围是
( )
A. B. C. D.
【答案】D
【解析】当 时,即 ,此时 恒成立,满足条件;
当 时,因为 对任意实数 都成立,所以 ,解得 ,
综上可知, ,故选:D.
4.已知奇函数 在 上单调递减,且 ,则不等式 的解集
为( )
A. B.
C. D.
【来源】山东省济南市历城区第二中学2021-2022学年高一下学期开学考试数学试题
【答案】A
【解析】因为奇函数 在 上单调递减,且 ,
所以 在 单调递减,且 ,
所以当 或 时, ,当 或 时, ,
当 时,不等式 等价于 ,
所以 或 ,解得 ,
当 时,不等式 等价于 ,
所以 或 ,解得 或 ,
综上,不等式的解集为 ,故选:A
5.已知函数 是定义在 上的偶函数,且在 单调递减,设
,则 的大小关系为( )
A. B. C. D.
【来源】湖北省武汉市汉阳一中、江夏一中2021-2022学年高一上学期12月联考数学试题
【答案】A
【解析】 函数 是定义在 上的偶函数,且在 上单调递减
则:
, ,∴ ,
即: 故选:A.6.已知定义在R上的奇函数f(x)满足 ,当 时, ,
则 ( )
A.2 B. C.-2 D.-
【来源】云南省峨山彝族自治县第一中学2021-2022学年高一下学期期中数学试题
【答案】A
【解析】:依题意, , ,
函数 的周期为6,
故 ,
又 ,则 .故选:A.
7.若 ,则 ( )
A. B.
C. D.
【来源】广东省佛山市顺德区乐从中学2021-2022学年高一下学期期中数学试题
【答案】C
,
因为
所以 , ,
因为 , ,
所以 , ,
则 .故选:C
8.已知函数 在区间 上是增函数,且在区间 上恰好取得一次最大值,则 的取值范围是( )
A. B. C. D.
【来源】宁夏回族自治区银川一中2021-2022学年高一下学期期中考试数学试题
【答案】B
【解析】
由 ,可得
由 在区间 上恰好取得一次最大值,可得 ,解之得
又 在区间 上是增函数,则 ,解之得
综上, 的取值范围是 故选:B
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项
符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知 , ,且 ,则下列说法正确的是( )
A. 的最小值为 B. 的最大值为
C. 的最大值为 D. 的最小值为
【来源】福建省福州第三中学2021-2022学年高一下学期期末考试数学试题
【答案】AB
【解析】:对于A:由 , , ,则 ,
所以 ,解得 ,
所以 ,所以当 时, 有最小值 ,故A正确.
对于B:由 , , ,即 ,当且仅当 ,即 ,
时等号成立,
所以 的最大值是 ,故B正确;
对于C:由 , , ,则 ,所以 ,解得 ,
所以 ,因为 ,所以 ,
所以 ,所以 ,即 ,故C错误;
对于D: ,
当且仅当 ,即 , 时取等号,故D错误;故选:AB
10.已知定义域为R的函数 在 上为增函数,且 为偶函数,则( )
A. 的图象关于直线x=-1对称 B. 在 上为增函数
C. D.
【答案】AD
【解析】因为 为偶函数,且函数 在 上为增函数,
所以 的图象关于直线x=-1对称,且 在 上为减函数,所以A正确,B
不正确;因为 的图象关于直线x=-1对称, ,所以C不正确;
因为 的图象关于直线x=-1对称,所以 , ,又
在 上为增函数,所以 ,即 ,所以D
正确.故选:AD.
11.已知 , 都是定义在 上的函数,其中 是奇函数, 是偶函数,且
,则下列说法正确的是( )A. 为偶函数 B.
C. 为定值 D.
【答案】ACD
【解析】因为 ,所以 ,又 是奇函数, 是偶
函数,所以 ,解得 , .
对于A, ,故 为偶函数,A正确;
对于B, ,故B错误;
对于C, ,故C正确;
对于D,当 时, , ;
当 时, , ,所以
,故D正确.
故选:ACD.
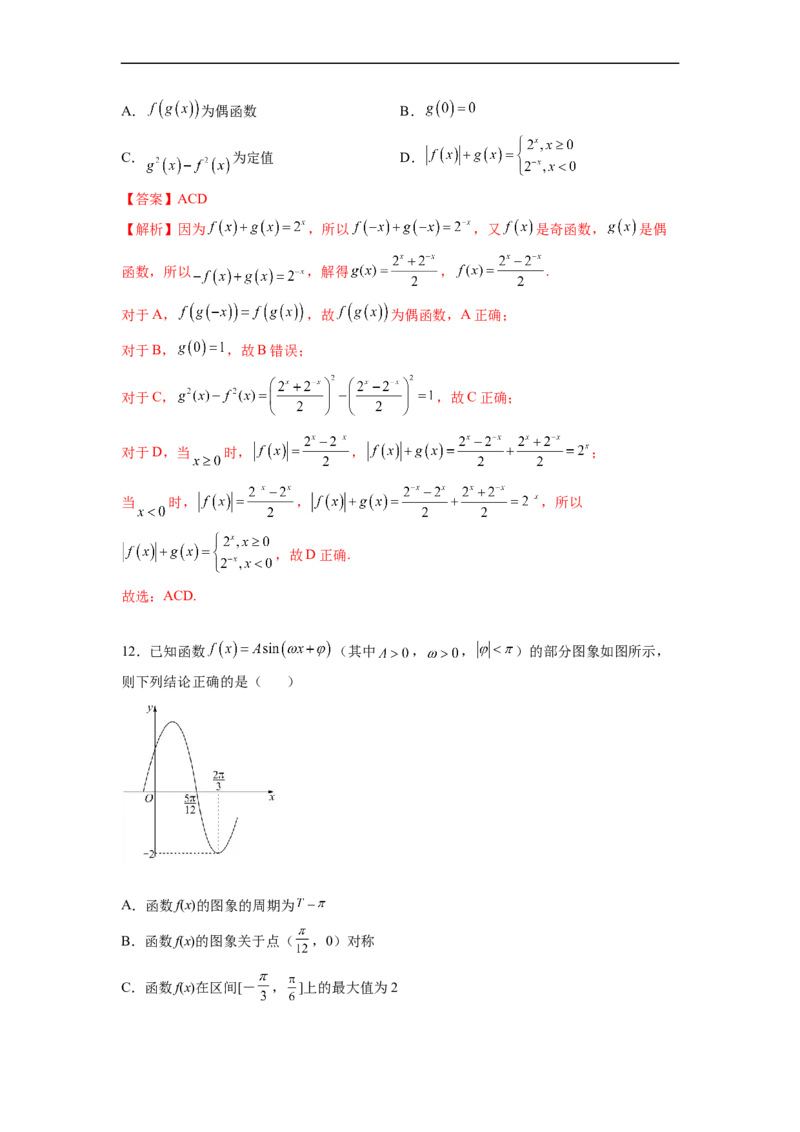
12.已知函数 (其中 , , )的部分图象如图所示,
则下列结论正确的是( )
A.函数f(x)的图象的周期为
B.函数f(x)的图象关于点( ,0)对称
C.函数f(x)在区间[- , ]上的最大值为2D.直线 与 )图像所有交点的横坐标之和为
【来源】5.4三角函数的图象与性质C卷
【答案】AC
【解析】依题意, ,得 ,故A正确;
, ,则 ,当 时, 取最小值,
则 ,得 ,即 ,
当 时, ,故B错误;
当 [- , ],则 ,则 ,故C正确;
,则 ,设直线 与 )图像所有交点
的横坐标为 ,则 ,解得 ,故D错误;
故选:AC
三 填空题:本题共4小题,每小题5分,共20分.
13.已知命题 :“ , ”,命题 :“ , ”, 的
否定是假命题, 是真命题,则实数 的取值范围是___________.
【答案】
【解析】由 , 得, ,因 的否定是假命题,则 是真命题,于是得
,
因 , ,即方程 有实根,则 ,解得 ,
又 是真命题,则 ,
因此,由 是真命题, 也是真命题,可得 ,
所以实数 的取值范围是 .故答案为:
14.方程 在区间 内有两个不同的根, 的取值范围为__.【答案】
【解析】:令 ,图象恒过点 ,
方程 0在区间 内有两个不同的根,
,解得 .
故答案为:
15.已知 是定义在 上的奇函数,当 时, 为增函数,且 ,那么不
等式 的解集是_______.
【来源】2.4.4 函数的奇偶性 (分层练习)-2022年初升高数学无忧衔接
【答案】
【解析】因 为奇函数,且在 上是增函数, ,
则 在 上是增函数,且 ,
不等式 化为: 或 ,解得 或
,
所以不等式 的解集是 .
故答案为:
16.已知函数 则函数 的值域为___________.若函数
有2个零点,则k的范围是___________.
【来源】江西省抚州市临川区第一中学2021-2022学年高一下学期第一次月考数学试题
【答案】 ; .
【解析】因为 ,
当 时,由 单调递增,
∴ 在 上单调递增,∴当 时, ,
当 时,所以 ,
综上,函数 的值域为 ,
作出函数 的图象与直线 如图所示:
函数 有2个零点,即 与 有2个交点,
所以 ,即 .
故答案为: ; .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知集合 , , .
(1)若 是“ ”的充分条件,求实数 的取值范围;
(2)若 ,求实数 的取值范围.
【答案】(1) ;(2) .
【解析】(1)因为 ,
所以 .因为 是 的充分条件,
所以 ,解得 ,∴ ;
(2)因为 , ,
所以 ,解得 .故 的取值范围为 .18.(12分)已知二次函数 同时满足以下条件:① ,② ,
③ .
(1)求函数 的解析式;
(2)若 , ,求:
① 的最小值 ;
②讨论关于m的方程 的解的个数.
【来源】四川省雅安中学2021-2022学年高一下学期3月月考数学试题
【答案】(1)
(2)① ;②答案见解析
【解析】(1)由 得,对称轴为 ,
设 ,
∴ ,得 ,
∴ .
(2)① , ,对称轴 ,
ⅰ当 即 时, 在 单调递增,
,
ⅱ 即 时, 在 单调递减,在 单调递增,
∴ ,
ⅲ当 即 时, 在 单调递减,
,
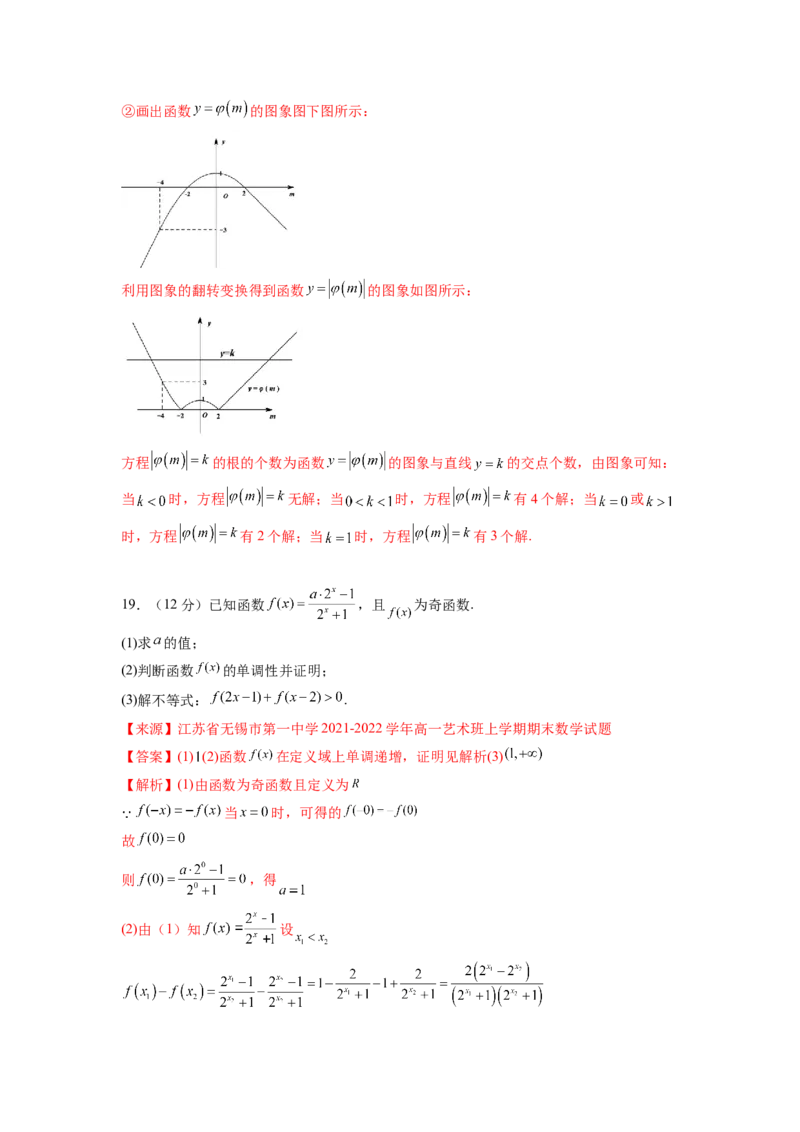
综上:②画出函数 的图象图下图所示:
利用图象的翻转变换得到函数 的图象如图所示:
方程 的根的个数为函数 的图象与直线 的交点个数,由图象可知:
当 时,方程 无解;当 时,方程 有4个解;当 或
时,方程 有2个解;当 时,方程 有3个解.
19.(12分)已知函数 ,且 为奇函数.
(1)求 的值;
(2)判断函数 的单调性并证明;
(3)解不等式: .
【来源】江苏省无锡市第一中学2021-2022学年高一艺术班上学期期末数学试题
【答案】(1) (2)函数 在定义域上单调递增,证明见解析(3)
【解析】(1)由函数为奇函数且定义为
当 时,可得的
故
则 ,得
(2)由(1)知 设由 在定义域内是单调增函数∵ ∴
即 ∴
即函数 在定义域上单调递增.
(3) ,且 为奇函数,
∴ ∵函数 单调递增
∴ ∴
∴不等式的解集为 .
20.(12分)已知函数 .
(1)求函数 在 上的单调区间;
(2)若 , ,求 的值.
【来源】甘肃省玉门油田第一中学2021-2022学年高一下学期期中考试数学试题
【答案】(1)递增区间为 , ,递减区间为 ;(2) .
【解析】(1)由题意得
,因为 ,所以 ,
令 ,解得 ;令 ,解得 ,
令 ,得 .
所以函数 在 上的单调递增区间为 , ,
单调递减区间为 .
(2)由(1)知 .因为 ,所以 ,
又因为 ,所以 ,
所以 .21.(12分)已知函数 ,且 的最小正周期
为 ,将 的图像沿x轴向左平移 个单位,得到函数 ,其中 为 的一条
对称轴.
(1)求函数 与 的解析式;
(2)若方程 在区间 有解,求实数t的取
值范围.
【来源】河南省驻马店市2021-2022学年高一下学期期末数学试题
【答案】(1) ; (2)
【解析】(1)由条件则
且 的最小正周期为 ,则
即 ,将 的图像沿 轴方向向左平移 个单位,
得到函数
且 为 的一条对称轴,即
由 可得
从而可得
.
(2)由(1)可知
记
即 ,
再记 ,,
代入 中,则 的值域求解问题等价于
, 的值域,
当 时, ;当 时,
因此 的值域为 ,也即 为
原命题“若方程 在区间 有解”
即等价于 在 内有解
只需 即可,解得 即为所求.
22.(12分)已知函数 是奇函数.
(1)求实数 的值; 并说明函数 的单调性(不证明);
(2)若对任意的实数 , 不等式 恒成立, 求实数
的取值范围.
【来源】湖北省宜昌市部分学校2021-2022学年高一下学期期中数学试题
【答案】(1)详见解析;(2)
【解析】(1)解:因为函数 是奇函数,
所以 ,解得 ,经检验符合题意;
此时 ,
因为 在R上是增函数, 在R上是减函数,
所以 在R上是增函数.
(2)因为对任意的实数 , 不等式 恒成立,
所以对任意的实数 , 不等式 恒成立,
所以对任意的实数 , 恒成立,所以对任意的实数 , 恒成立,
令 ,
所以 ,
实数 的取值范围 .