文档内容
高二年级下学期期末仿真卷 01
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.等差数列{a}前n项和为S,a+a=5,则S=( )
n n 3 4 6
A.15 B.20 C.25 D.30
2.(2x﹣ )5的展开式中x3项的系数为( )
A.80 B.﹣80 C.﹣40 D.48
3.设f(x)存在导函数且满足 =﹣1,则曲线y=f(x)上的点(1,f(1))处的
切线的斜率为( )
A.﹣1 B.﹣2 C.1 D.2
4.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.
问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所
得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重
量单位).这个问题中,甲所得为( )
A. 钱 B. 钱 C. 钱 D. 钱
5.设x=﹣ 是函数f(x)=ln(x+2)﹣ax2﹣3a2x的极小值点,则f(x)的极大值为( )
A.2 B.1 C. D.
6.2019年10月17日是我国第6个“扶贫日”,某医院开展扶贫日“送医下乡”医疗义诊活动,现有五名
医生被分配到四所不同的乡镇医院中,医生甲被指定分配到医院 A,医生乙只能分配到医院A或医院
B,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有( )
A.18种 B.20种 C.22种 D.24种
7.2019年10月1日在庆祝中华人民共和国成立 70周年大阅兵的徒步方队中,被誉为“最强大脑”的院校
科研方队队员分别由军事科学院、国防大学、国防科技大学三所院校联合抽组,已知军事科学学院的甲、
乙、丙三名同学被选上的概率分别为 , , ,这三名同学中至少有一名同学被选上的概率为
( )
A. B. C. D.
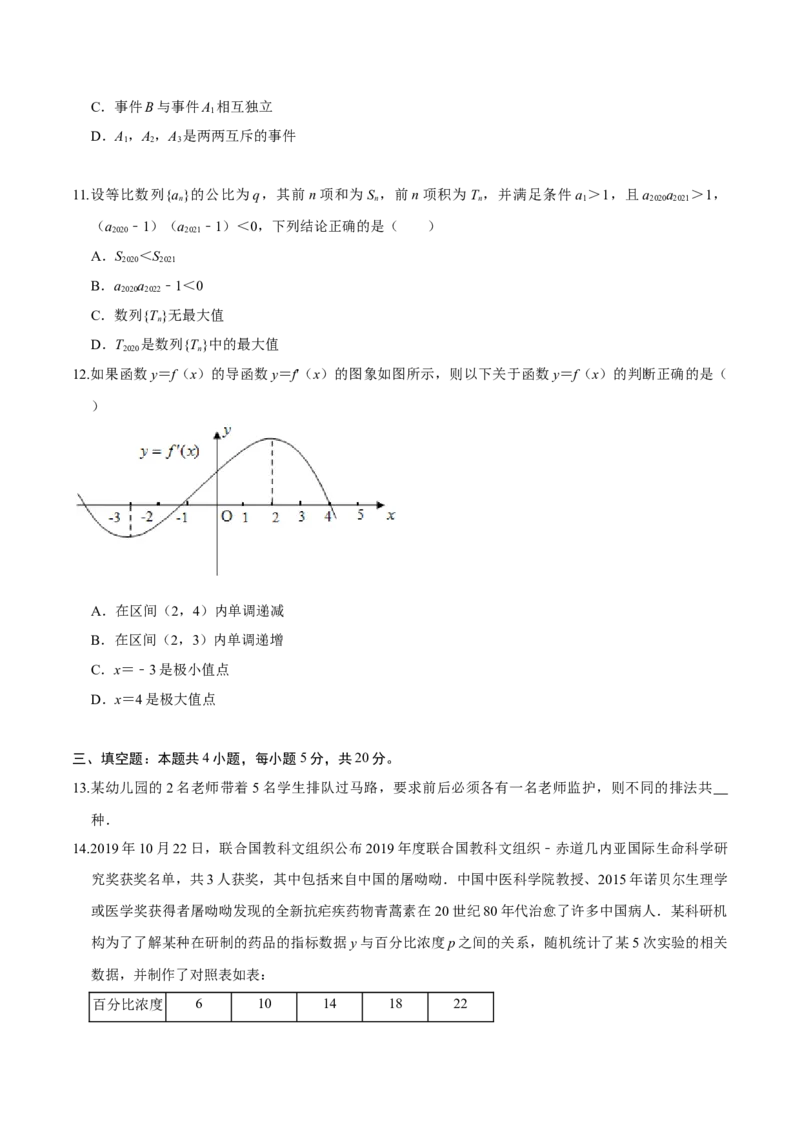
8.某种商品的广告费支出x与销售额y(单位:万元)之间有如下对应数据,根据表中提供的数据,得出 y
与x的线性回归方程为 ,则表中的m的值为( )
x 2 4 5 6 8
y 30 40 m 50 70
A.45 B.50 C.55 D.60
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。
9.对于二项式 ,以下判断正确的有( )
A.存在n N*,展开式中有常数项
B.对任意∈n N*,展开式中没有常数项
C.对任意n∈N*,展开式中没有x的一次项
D.存在n N∈*,展开式中有x的一次项
10.甲罐中有5∈个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取
出一球放入乙罐,分别以A ,A 和A 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随
1 2 3
机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是( )
A.
B.C.事件B与事件A 相互独立
1
D.A,A,A 是两两互斥的事件
1 2 3
11.设等比数列{a}的公比为q,其前n项和为S ,前n项积为T ,并满足条件a >1,且a a >1,
n n n 1 2020 2021
(a ﹣1)(a ﹣1)<0,下列结论正确的是( )
2020 2021
A.S <S
2020 2021
B.a a ﹣1<0
2020 2022
C.数列{T}无最大值
n
D.T 是数列{T}中的最大值
2020 n
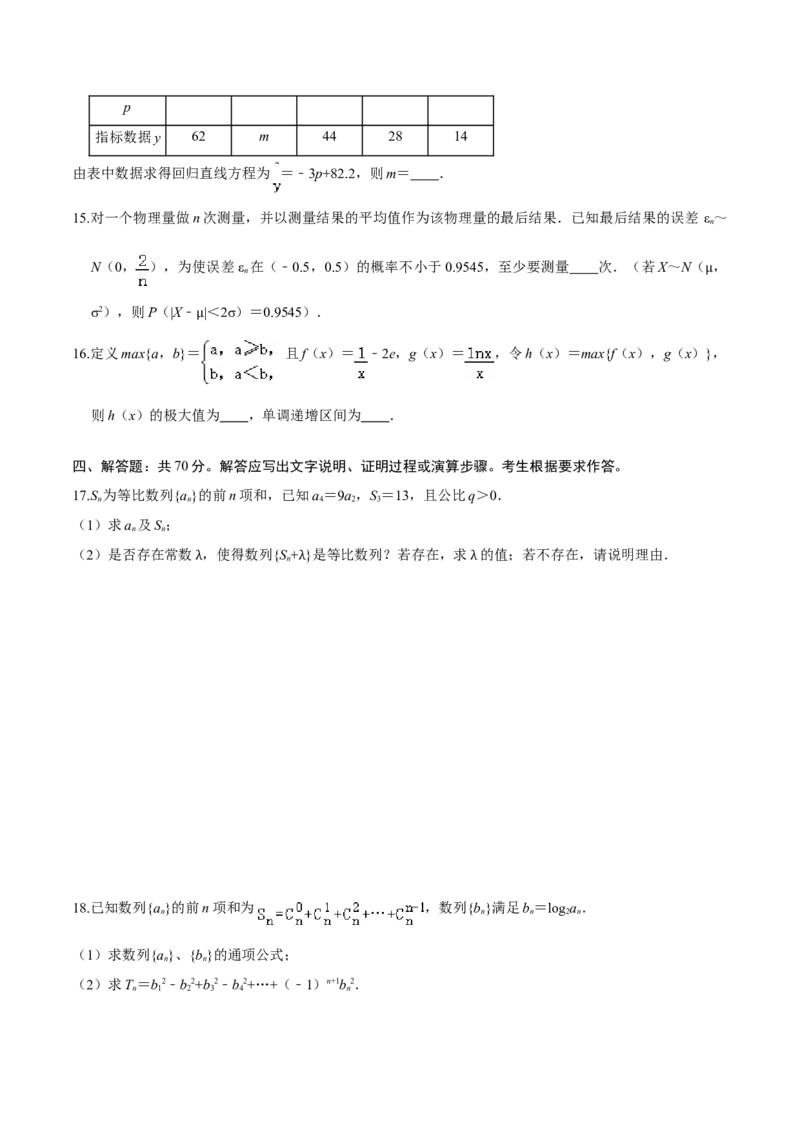
12.如果函数y=f(x)的导函数y=f'(x)的图象如图所示,则以下关于函数y=f(x)的判断正确的是(
)
A.在区间(2,4)内单调递减
B.在区间(2,3)内单调递增
C.x=﹣3是极小值点
D.x=4是极大值点
三、填空题:本题共4小题,每小题5分,共20分。
13.某幼儿园的2名老师带着5名学生排队过马路,要求前后必须各有一名老师监护,则不同的排法共
种.
14.2019年10月22日,联合国教科文组织公布2019年度联合国教科文组织﹣赤道几内亚国际生命科学研
究奖获奖名单,共3人获奖,其中包括来自中国的屠呦呦.中国中医科学院教授、2015年诺贝尔生理学
或医学奖获得者屠呦呦发现的全新抗疟疾药物青蒿素在20世纪80年代治愈了许多中国病人.某科研机
构为了了解某种在研制的药品的指标数据y与百分比浓度p之间的关系,随机统计了某5次实验的相关
数据,并制作了对照表如表:
百分比浓度 6 10 14 18 22p
指标数据y 62 m 44 28 14
由表中数据求得回归直线方程为 =﹣3p+82.2,则m= .
15.对一个物理量做n次测量,并以测量结果的平均值作为该物理量的最后结果.已知最后结果的误差 ε ~
n
N(0, ),为使误差ε 在(﹣0.5,0.5)的概率不小于0.9545,至少要测量 次.(若X~N( ,
n
μ
σ2),则P(|X﹣ |<2σ)=0.9545).
μ
16.定义max{a,b}= 且f(x)= ﹣2e,g(x)= ,令h(x)=max{f(x),g(x)},
则h(x)的极大值为 ,单调递增区间为 .
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.S 为等比数列{a}的前n项和,已知a=9a,S=13,且公比q>0.
n n 4 2 3
(1)求a 及S;
n n
(2)是否存在常数 ,使得数列{S+ }是等比数列?若存在,求 的值;若不存在,请说明理由.
n
λ λ λ
18.已知数列{a}的前n项和为 ,数列{b}满足b=log a.
n n n 2 n
(1)求数列{a}、{b}的通项公式;
n n
(2)求T=b2﹣b2+b2﹣b2+…+(﹣1)n+1b2.
n 1 2 3 4 n19.为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大
师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学
工作.某教育机构为了了解人们对其数学网课授课方式的满意度,从经济不发达的 A城市和经济发达的
B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
若评分不低于80分,则认为该用户对此教育机构授课方式“认可”,否则认为该用户对此教育机构授课方
式“不认可”.
(Ⅰ)请根据此样本完成下列2×2列联表,并据此列联表分析,能否有95%的把握认为城市经济状况与该
市的用户认可该教育机构授课方式有关?
认可 不认可 合计
A城市
B城市
合计
(Ⅱ)以该样本中A,B城市的用户对此教育机构授课方式“认可”的频率分别作为 A,B城市用户对此教
育机构授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户,用X表示这
4个用户中对此教育机构授课方式“认可”的用户个数,求x的分布列.
参考公式: ,其中n=a+b+c+d.
参考数据:
P(K2≥K) 0.10 0.05 0.025
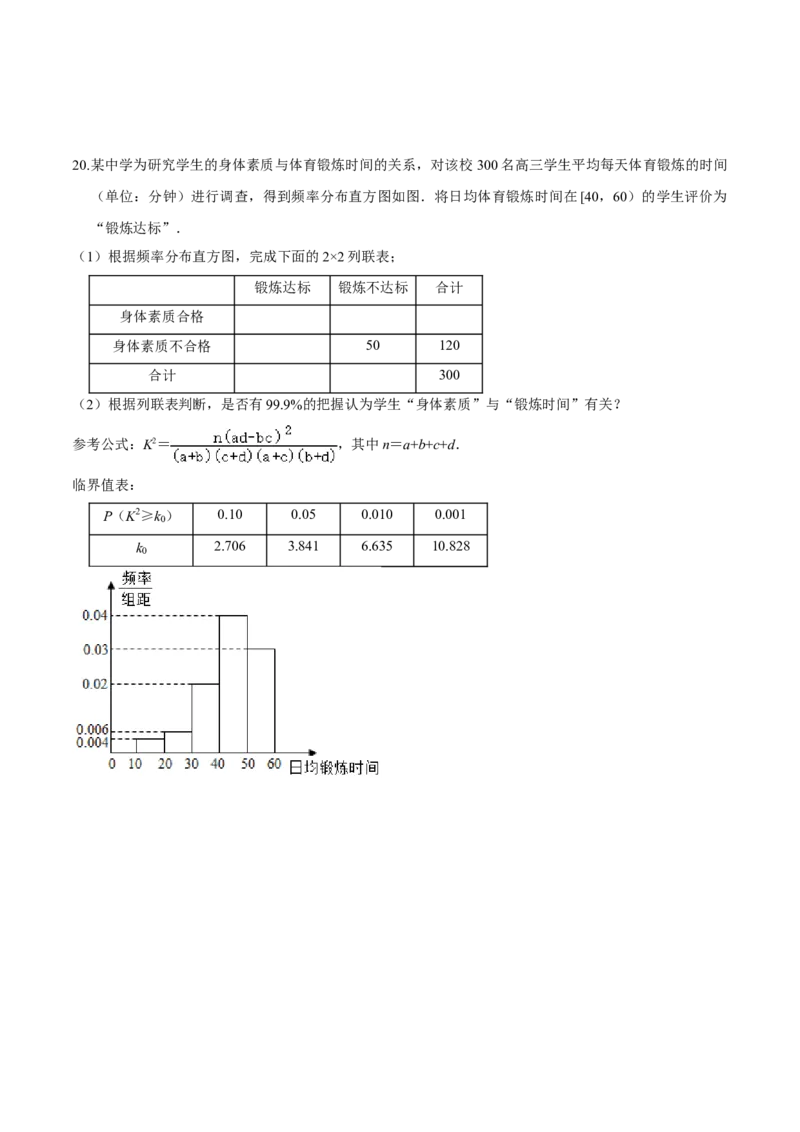
k 2.706 3.841 5.02420.某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼的时间
(单位:分钟)进行调查,得到频率分布直方图如图.将日均体育锻炼时间在[40,60)的学生评价为
“锻炼达标”.
(1)根据频率分布直方图,完成下面的2×2列联表;
锻炼达标 锻炼不达标 合计
身体素质合格
身体素质不合格 50 120
合计 300
(2)根据列联表判断,是否有99.9%的把握认为学生“身体素质”与“锻炼时间”有关?
参考公式:K2= ,其中n=a+b+c+d.
临界值表:
P(K2≥k ) 0.10 0.05 0.010 0.001
0
k 2.706 3.841 6.635 10.828
021.在集合A={1,2,3,4,…,2n}中,任取m(m≤n,m,n N*)元素构成集合A .若A 的所有元素
m m
之和为偶数,则称A 为A的偶子集,其个数记为f(m);若∈ A 的所有元素之和为奇数,则称A 为A
m m m
的奇子集,其个数记为g(m).令F(m)=f(m)﹣g(m).
(1)当n=2时,求F(1),F(2)的值;
(2)求F(m).
22.已知函数f(x)=(x﹣1)lnx+ax2+(1﹣a)x﹣1.
(1)当a=﹣1时,判断函数的单调性;
(2)讨论f(x)零点的个数.