文档内容
高二年级下学期期末仿真卷 02
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知各项为正数的等比数列{a}中,a=1,aa=64,则公比q=( )
n 2 4 6
A.4 B.3 C.2 D.
【答案】C
【分析】利用等比数列的通项公式列方程组,能求出公比.
【解答】解:∵各项为正数的等比数列{a}中,a=1,aa=64,
n 2 4 6
∴ ,且q>0,
解得 = ,q=2,
∴公比q=2.
故选:C.
【知识点】等比数列的性质
2.从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有( )
A.4种 B.12种 C.24种 D.64种
【答案】C
【分析】分析易得,这是一个排列问题,由排列公式计算可得答案;
【解答】解:根据题意,这是一个排列问题,
故从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有A3=4×3×2=24种.
4
故选:C.
【知识点】计数原理的应用
3.直线 与曲线 相切,则b的值为( )
A.﹣2 B.﹣1 C. D.1
【答案】B
【分析】先设出切点坐标,根据导数的几何意义求出在切点处的导数,从而求出切点横坐标,再根据切点既在直线 的图象上又在曲线 上,即可求出b的值.
【解答】解:设切点坐标为(m,n)
y′| =﹣ =
x=m
解得 m=1
∵切点(1,n)在曲线 的图象上,
∴n=﹣ ,
∵切点(1,﹣ )又在直线 上,
∴b=﹣1.
故选:B.
【知识点】利用导数研究曲线上某点切线方程
4.若函数f(x)=alnx﹣x2+5x在(1,3)内无极值点,则实数a的取值范围是( )
A.(﹣ ,3) B.(﹣∞,﹣ )
C.[3,+∞) D.(﹣∞,﹣ ]∪[3,+∞)
【答案】D
【分析】求出函数的导数,题目转化为导函数在(1,3)内无零点,构造函数,利用二次函数的性质求解
函数的值域,借助函数的图象,推出结果.
【解答】 解:函数f(x)=alnx﹣x2+5x,f′(x)= =0,
即a=2x2﹣5x,在(1,3)内无解,
设h(x)=2x2﹣5x=2(x﹣ )2﹣ ,x (1,3),
∈
则h(x) =﹣ ,h(1)=﹣3,h(3)=3,
min
由函数h(x)的图象可知,
实数a的取值范围:(﹣∞,﹣ ]∪[3,+∞).
故选:D.【知识点】利用导数研究函数的极值
5.已知集合A={1,2,3,4},B={1,2,3,4,5},从集合A中任取3个不同的元素,其中最小的元素
用a表示,从集合B中任取3个不同的元素,其中最大的元素用b表示,记X=b﹣a,则随机变量X的
期望为( )
A. B. C.3 D.4
【答案】A
【分析】根据题意,确定集合A和集合B的可能集合,以及a和b的取值,确定X=b﹣a的取值为1,2,
3,4,分别求出X取不同值时的概率,列出随机变量X的分布列,根据期望的运算公式代入数值
求解即可.
【解答】解:根据题意,
从集合A中任取3个不同的元素,则集合A有4种可能,分别为:{1,2,3},{1,2,4},
{1,3,4},{2,3,4},其中最小的元素a取值分别为:1,2.
从集合B中任取3个不同的元素,则集合B有10种可能,分别为:{1,2,3},{1,2,4},
{1,2,5},{1,3,4},{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,
4,5},其中最大的元素b取值分别为:3,4,5.
∵X=b﹣a,则X的取值为:1,2,3,4.
P(X=1)= = ;
P(X=2)= = = ;
P(X=3)= = = ;
P(X=4)= = = .
随机变量X的分布列如下:
X 1 2 3 4
P
E(X)=1× +2× +3× +4× = .
故选:A.
【知识点】离散型随机变量的期望与方差
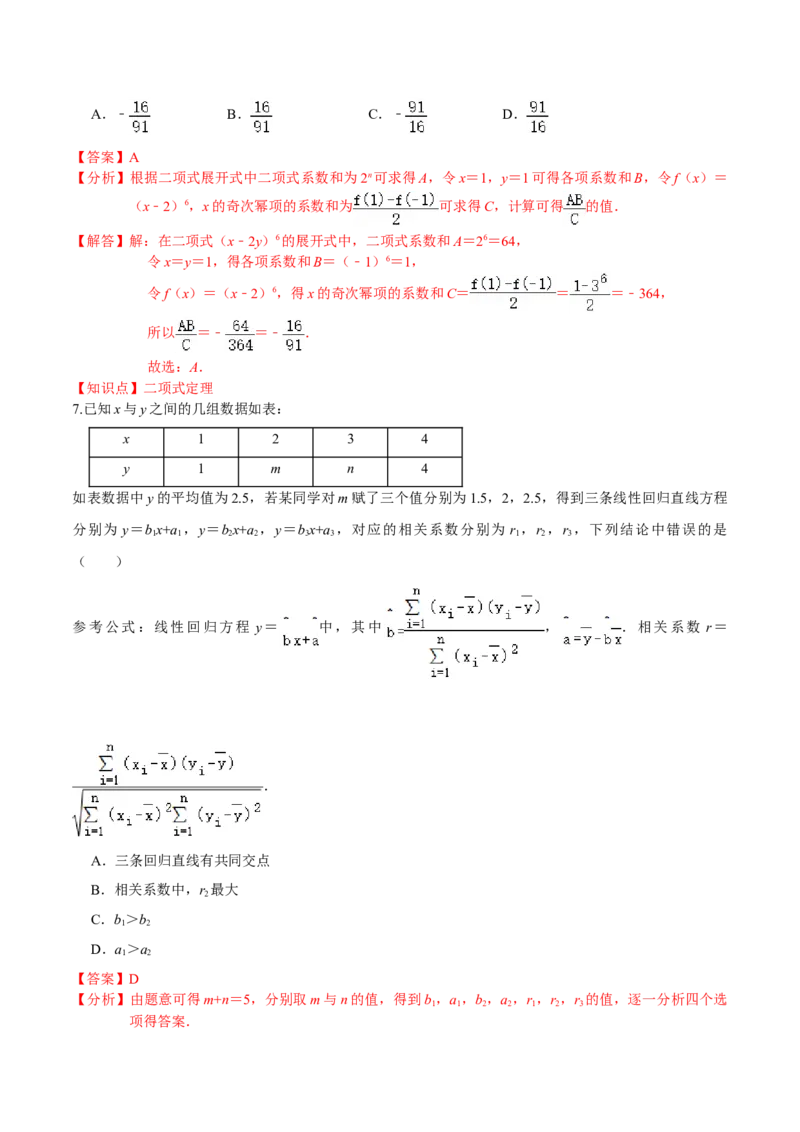
6.在二项式(x﹣2y)6的展开式中,设二项式系数和为A,各项系数和为B,x的奇次幂项的系数和为C,
则 =( )A.﹣ B. C.﹣ D.
【答案】A
【分析】根据二项式展开式中二项式系数和为2n可求得A,令x=1,y=1可得各项系数和B,令f(x)=
(x﹣2)6,x的奇次幂项的系数和为 可求得C,计算可得 的值.
【解答】解:在二项式(x﹣2y)6的展开式中,二项式系数和A=26=64,
令x=y=1,得各项系数和B=(﹣1)6=1,
令f(x)=(x﹣2)6,得x的奇次幂项的系数和C= = =﹣364,
所以 =﹣ =﹣ .
故选:A.
【知识点】二项式定理
7.已知x与y之间的几组数据如表:
x 1 2 3 4
y 1 m n 4
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程
分别为 y=bx+a ,y=bx+a ,y=bx+a ,对应的相关系数分别为 r ,r ,r ,下列结论中错误的是
1 1 2 2 3 3 1 2 3
( )
参考公式:线性回归方程 y= 中,其中 , .相关系数 r=
.
A.三条回归直线有共同交点
B.相关系数中,r 最大
2
C.b>b
1 2
D.a>a
1 2
【答案】D
【分析】由题意可得m+n=5,分别取m与n的值,得到b ,a ,b ,a ,r ,r ,r 的值,逐一分析四个选
1 1 2 2 1 2 3
项得答案.【解答】解:由题意,1+m+n+4=10,即m+n=5.
若m=1.5,则n=3.5,此时 , .
=(1﹣2.5)(1﹣2.5)+(2﹣2.5)(1.5﹣2.5)
+(3﹣2.5)(3.5﹣2.5)+(4﹣2.5)(4﹣2.5)=5.5,
=(﹣1.5)2+(﹣0.5)2+0.52+1.52=5,
=(﹣1.5)2+(﹣1)2+12+1.52=6.5.
则 ,a=2.5﹣1.1×2.5=﹣0.25, ;
1
若m=2,则n=3,此时 , .
=(1﹣2.5)(1﹣2.5)+(2﹣2.5)(2﹣2.5)+(3﹣2.5)(3﹣
2.5)+(4﹣2.5)(4﹣2.5)=5,
=5, =(﹣1.5)2+(﹣0.5)2+0.52+1.52=5.
,a=2.5﹣1×2.5=0, ;
2
若m=2.5,则n=2.5,此时 , .
=(1﹣2.5)(1﹣2.5)+(2﹣2.5)(2.5﹣2.5)
+(3﹣2.5)(2.5﹣2.5)+(4﹣2.5)(4﹣2.5)=4.5,
=5, =(﹣1.5)2+1.52=4.5, .
由样本点的中心相同,故A正确;
由以上计算可得,相关系数中,r 最大,b>b,a<a,故B,C正确,D错误.
2 1 2 1 2
故选:D.
【知识点】线性回归方程
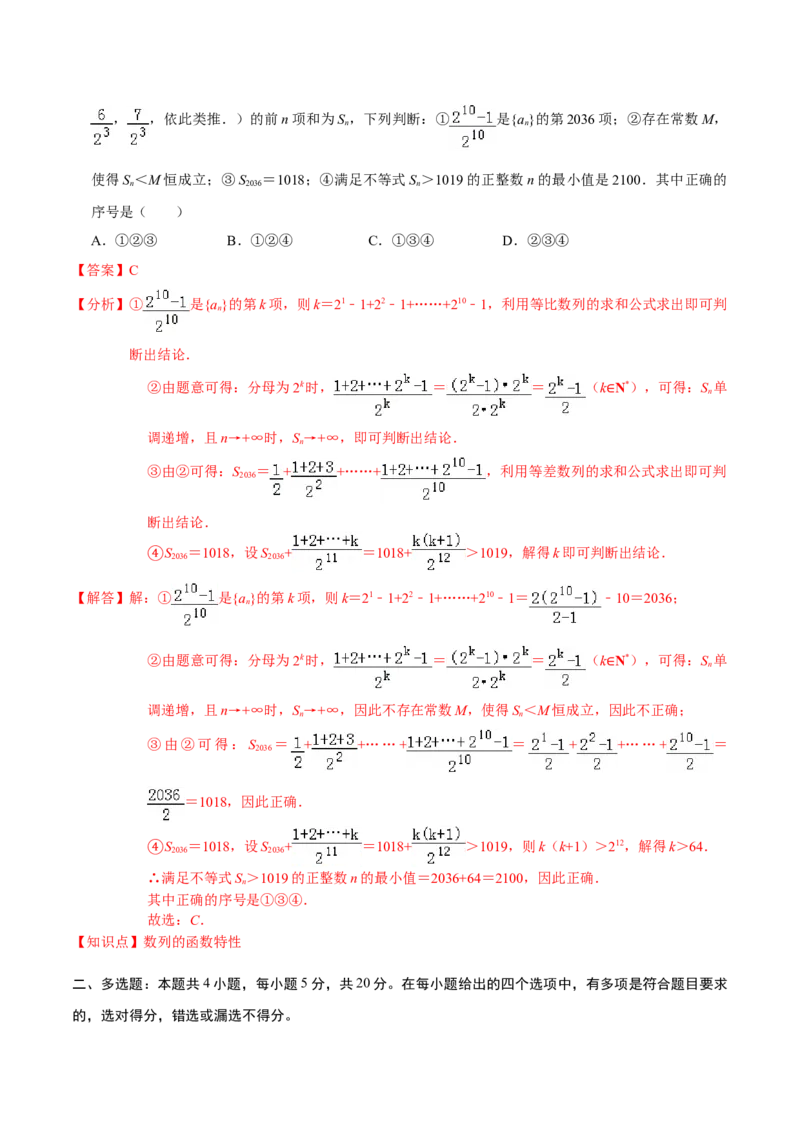
8.已知数列{a}: , , , , , , , , , , , , ,…(其中第一
n
项是 ,接下来的22﹣1项是 , ,再接下来的23﹣1项是 , , , , ,, ,依此类推.)的前n项和为S ,下列判断:① 是{a}的第2036项;②存在常数M,
n n
使得S <M恒成立;③S =1018;④满足不等式S >1019的正整数n的最小值是2100.其中正确的
n 2036 n
序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
【答案】C
【分析】① 是{a}的第k项,则k=21﹣1+22﹣1+……+210﹣1,利用等比数列的求和公式求出即可判
n
断出结论.
②由题意可得:分母为2k时, = = (k N*),可得:S 单
n
∈
调递增,且n→+∞时,S→+∞,即可判断出结论.
n
③由②可得:S = + +……+ ,利用等差数列的求和公式求出即可判
2036
断出结论.
S =1018,设S + =1018+ >1019,解得k即可判断出结论.
2036 2036
④
【解答】解:① 是{a}的第k项,则k=21﹣1+22﹣1+……+210﹣1= ﹣10=2036;
n
②由题意可得:分母为2k时, = = (k N*),可得:S 单
n
∈
调递增,且n→+∞时,S→+∞,因此不存在常数M,使得S<M恒成立,因此不正确;
n n
③由②可得:S = + +……+ = + +……+ =
2036
=1018,因此正确.
S =1018,设S + =1018+ >1019,则k(k+1)>212,解得k>64.
2036 2036
④∴满足不等式S>1019的正整数n的最小值=2036+64=2100,因此正确.
n
其中正确的序号是①③④.
故选:C.
【知识点】数列的函数特性
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。9.已知数列{a}是等差数列,其前n项和为S,满足a+3a=S,则下列四个选项中正确的有( )
n n 1 2 6
A.a=0 B.S =0 C.S 最小 D.S=S.
7 13 7 5 8
【答案】ABD
【分析】根据题意,设等差数列{a}的公差为d,据此由等差数列的前n项和公式依次分析选项,综合即可
n
得答案.
【解答】解:根据题意,设等差数列{a}的公差为d,
n
对于A,若a+3a=S,即4a+3d=6a+ d,变形可得:a+6d=0,即a=0,故A正确;
1 2 6 1 1 1 7
对于B,S = =13a=0,B正确;
13 7
对于C,S= =7a,可能大于0,也可能小于0,因此C不正确;
7 4
对于D,S﹣S=(5a+ d)﹣(8a+ d)=﹣3a﹣18d=﹣3a=0,D正确.
5 8 1 1 1 7
故选:ABD.
【知识点】等差数列的前n项和
10.现有3个男生4个女生,若从中选取3个学生,则( )
A.选取的3个学生都是女生的不同选法共有4种
B.选取的3个学生恰有1个女生的不同选法共有24种
C.选取的3个学生至少有1个女生的不同选法共有34种
D.选取的3个学生至多有1个男生的不同选法共有18种
【答案】AC
【分析】根据组合的定义和分步计数原理即可求出.
【解答】解:选取的3个学生都是女生的不同的选法共有C 3=4,故A正确;
4
恰有1个女生的不同选法共有C 2C 1=12种,故B错误;
3 4
至少有1个女生的不同选法共有C 3﹣C 3=34种,故C正确;
7 3
选取的3个学生至多有1个男生的不同选法共C 1C 2+C 3=22种,故D错误.
3 4 4
故选:AC.
【知识点】排列、组合及简单计数问题
11.如图所示,5个(x,y)数据,去掉D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变小D.解释变量x与预报变量y的相关性变强
【答案】AD
【分析】由散点图知,去掉离群点D后,x与y的相关性变强,且为正相关,由此判断即可.
【解答】解:由散点图知,去掉离群点D后,x与y的相关性变强,且为正相关,
所以相关系数r的值变大,相关指数R2的值变大,残差平方和变小.
故选:AD.
【知识点】变量间的相关关系、相关系数
12.已知函数f(x)的定义域为(0,+∞),导函数为f′(x),xf′(x)﹣f(x)=xlnx,且 ,
则( )
A.f′( )=0
B.f(x)在 处取得极大值
C.0<f(1)<1
D.f(x)在(0,+∞)单调递增
【答案】ACD
【分析】令g(x)= ,则g′(x)= = ,设g(x)= ,得f
(x)= ,结合f( )= 求得c,可得f(x)的解析式,求导后逐一核对四个选项
得答案.
【解答】解:令g(x)= ,则g′(x)= = ,
∴g(x)= ,即 ,
则f(x)= .
又f( )= ,∴c= .
则f(x)= .
f′(x)= = ≥0,
则f′( )=0,故A正确;
f(x)在(0,+∞)单调递增,故B错误,D正确;
f(1)= ∈(0,1),故C正确.
故选:ACD.
【知识点】利用导数研究函数的单调性三、填空题:本题共4小题,每小题5分,共20分。
13.函数f(x)=(2x﹣x2)ex取得极小值时的x值为 .
【分析】求出函数的导数,令导数大于0,得增区间,令导数小于0,得减区间,再由极值的定义,即可得
到所求.
【解答】解:∵函数f(x)=(2x﹣x2)ex,
∴f′(x)=(2﹣x2)ex=ex( x)( ),
由f′(x)<0,解得x> 或x< ;
由f′(x)>0,解得 <x< .
即有f(x)的单调减区间为(﹣∞, ),( ,+∞),
单调递增区间为( , ),
则有x= 处f(x)取得极大值,
在x= 处f(x)取得极小值.
故答案为: .
【知识点】利用导数研究函数的极值
14.已知(x﹣ )(1﹣x)4的展开式中x2的系数为4,则a= ,(x﹣ )(1﹣x)4的展开式中的常数
项为 .
【答案】【第1空】2
【第2空】8
【分析】把(1﹣x)4按照二项式定理展开,可得(x﹣ )(1﹣x)4的展开式中x2的系数和常数项.
【解答】解:∵(x﹣ )(1﹣x)4=(x﹣ )( ﹣ •x+ •x2﹣ •x3+ •x4),
故展开式中x2的系数为﹣4+a× =4,则a=2.
常数项为﹣a×(﹣ )=4a=8,
故答案为:2;8.
【知识点】二项式定理
15.用数学归纳法证明(n+1)(n+2)(n+3)…(n+n)=2n•1•3•5…(2n﹣1)(n N*)时,从n=k到n
=k+1时左边需增乘的代数式是 . ∈
【答案】4k+2
【分析】从n=k到n=k+1时左边需增乘的代数式是 ,化简即可得出.
【解答】解:用数学归纳法证明(n+1)(n+2)(n+3)…(n+n)=2n•1•3•5…(2n﹣1)(n N*)时,
从n=k到n=k+1时左边需增乘的代数式是 =2(2k+1).
∈
故答案为:4k+2.
【知识点】数学归纳法16.已知一袋中有标有号码1、2、3、4的卡片各一张,每次从中取出一张,记下号码后放回,当四种号码
的卡片全部取出时即停止,则恰好取6次卡片时停止的概率为 .
【分析】恰好取6次卡片时停止,说明前5次出现了3种号码且前6次出现第四种号码.分两类,三种号
码出现的次数分别为3,1,1或者2,2,1.每类中可以分步完成,先确定三种号码卡片出现顺
序为 种,再分别确定这三种号码卡片出现的位置(注意平均分组问题),最后让第四种号码卡
片出现有一种方法,相乘可得,最后根据古典概型求概率即可.
【解答】解:由分步计数原理知,每次从中取出一张,记下号码后放回,进行6次一共有45种不同的取法.
恰好取6次卡片时停止,说明前5次出现了3种号码且第6次出现第4种号码,三种号码出现
的次数分别为3,1,1或者2,2,1.
三种号码分别出现3,1,1且6次时停止的取法由 ,
三种号码分别出现2,2,1且6次时停止的取法由 ,
由分步加法计数原理知恰好取6次卡片时停止,共有240+360=600种取法,
所以恰好取6次卡片时停止的概率为P= ,
故答案为 .
【知识点】n次独立重复试验中恰好发生k次的概率
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.已知F(x)= t(t﹣4)dt,x (﹣1,+∞).
∈
(1)求F(x)的单调区间;
(2)求函数F(x)在[1,5]上的最值.
【分析】先由定积分的运算求得F(x)的解析式,
(1)求导,令F′(x)>0,可求得增区间,令F′(x)<0,可求得减区间;
(2)由(1)可得函数F(x)在[1,5]上的单调性,再比较在x=1,x=4及x=5处的函数值
大小,进而得到最值.
【解答】解: = .
(1)F′(x)=x2﹣4x=x(x﹣4),由F′(x)>0,得﹣1<x<0或x>4;由F′(x)<
0,得0<x<4,
所以F(x)的单调递增区间为(﹣1,0)和(4,+∞),单调递减区间为(0,4).
(2)由(1)知F(x)在[1,4]上递减,在[4,5]上递增,
因为F(1)= ,F(4)=﹣ ,F(5)=﹣6,所以F(x)在[1,5]上的最大值为 ,最小值为﹣ .
【知识点】利用导数研究函数的单调性
18.某校寒假行政值班安排,要求每天安排一名行政人员值日,现从包含甲、乙两人的七名行政人员中选四
人负责四天的轮班值日,在下列条件下,各有多少种不同的安排方法?
(1)甲、乙两人都被选中,且安排在前两天值日;
(2)甲、乙两人只有一人被选中,且不能安排在后两天值日.
【分析】(1)根据题意,分2步进行分析:①甲、乙两人安排在前两天值日,②从剩下的五人中选两人安
排在后两天排列值日,由分步计数原理计算可得答案;
(2)根据题意,分2步进行分析:①从甲、乙两人中选一人安排在前两天中的一天值日,②
从剩下的五人中选三人安排在剩余的三天值日,由分步计数原理计算可得答案.
【解答】解:(1)根据题意,分2步进行分析:①甲、乙两人安排在前两天值日,有 种排法,
②从剩下的五人中选两人安排在后两天排列值日,有 种排法.
则排法种数为 .
(2)根据题意,分2步进行分析:①从甲、乙两人中选一人安排在前两天中的一天值日,有
种排法.
②从剩下的五人中选三人安排在剩余的三天值日,有 种排法.
则满足条件的排法种数为 .
【知识点】排列、组合及简单计数问题
19.已知 的展开式中第2项与第3项的二项式系数之比是1:3.
(1)求n的值;
(2)求二项展开式中各项二项式系数和以及各项系数和;
(3)求展开式中系数的绝对值最大的项.
【分析】(1)由 : =1:3,可解得n;
(2)二项式系数和2n,令x=1可得各项系数和;
(3)通过列不等式组即可求展开式中系数的绝对值最大的项.
【解答】解:(1)由题意得 : =1:3,即 = ,解得n=7;
(2)二项展开式中各项二项式系数和为27=128,
令x=1可得各项系数和为(3﹣2)7=1;
(3) 展开式的通项公式为T = ,
r+1设展开式中系数的绝对值最大的项为T ,
r+1
则 ,
解得 ≤r≤ ,∴r=3,
∴展开式中系数的绝对值最大的项为T=﹣22680 .
4
【知识点】二项式定理
20.近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为 21
世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了
两款电动汽车车型A和车型B,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情
况,制造商随机调查了5家汽车4S店的销量(单位:台),得到如表:
4S店 甲 乙 丙 丁 戊
车型A 6 6 13 8 1l
车型B 12 9 13 6 4
(Ⅰ)若从甲、乙两家4S店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的
2台电动汽车中至少有1台是车型A的概率;
(Ⅱ)现从这5家汽车4S店中任选3家举行促销活动,用X表示其中车型A销量超过车型B销量的4S店
的个数,求随机变量X的分布列和数学期望.
【分析】(Ⅰ)先根据古典概型依次求出从甲、乙4S店分别随机抽取的1台电动汽车是车型B的概率,然
后依据独立事件的概率和从对立事件的角度出发求解问题即可;
(Ⅱ)由表可知,车型A销量超过车型B销量的4S店有2家,故X的可能取值为0,1,2,然
后根据超几何分布求概率的方法逐一求出每个X的取值所对应的概率即可得分布列,进而求得
数学期望.
【解答】解:(Ⅰ)设“从甲4S店随机抽取的1台电动汽车是车型B”为事件M ,“从乙4S店随机抽取
1
的1台电动汽车是车型B”为事件M,
2
则 , ,且事件M、M 相互独立,
1 2
设“抽取的2台电动汽车中至少有1台是车型A”为事件M,
则 .
(Ⅱ)由表可知,车型A销量超过车型B销量的4S店有2家,故X的可能取值为0,1,2,
P(X=0)= ,
P(X=1)= ,P(X=2)= .
∴随机变量X的分布列为
X 0 1 2
P
数学期望E(X)= .
【知识点】离散型随机变量及其分布列、离散型随机变量的期望与方差
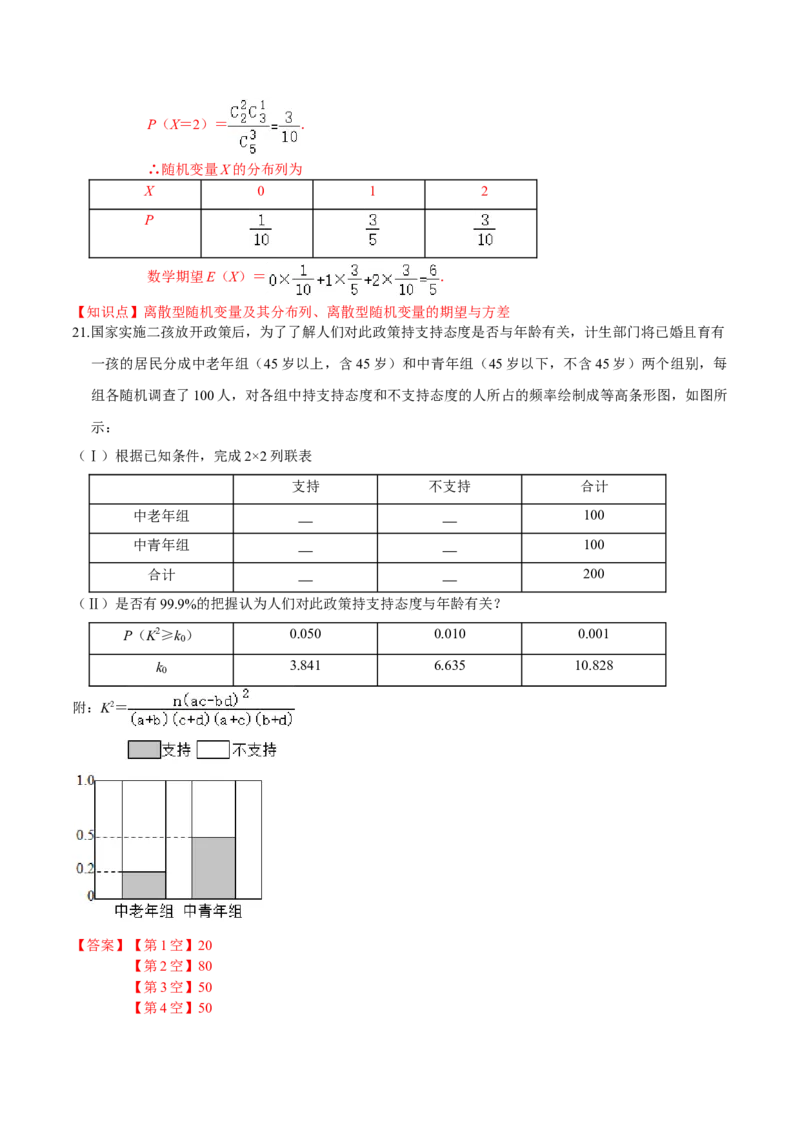
21.国家实施二孩放开政策后,为了了解人们对此政策持支持态度是否与年龄有关,计生部门将已婚且育有
一孩的居民分成中老年组(45岁以上,含45岁)和中青年组(45岁以下,不含45岁)两个组别,每
组各随机调查了100人,对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图,如图所
示:
(Ⅰ)根据已知条件,完成2×2列联表
支持 不支持 合计
中老年组 100
中青年组 100
合计 200
(Ⅱ)是否有99.9%的把握认为人们对此政策持支持态度与年龄有关?
P(K2≥k ) 0.050 0.010 0.001
0
k 3.841 6.635 10.828
0
附:K2=
【答案】【第1空】20
【第2空】80
【第3空】50
【第4空】50【第5空】70
【第6空】130
【分析】(Ⅰ)利用已知条件直接完成2×2列联表.
(Ⅱ)求出K2的观测值,则结论可求.
【解答】解:(Ⅰ)由等高条形图可知:
中老年组中,持支持态度的有20人,持不支持态度的有80人;
中青年组中,持支持态度的有50人,持不支持态度的有50人.
故2×2列联表为:
支持 不支持 合计
中老年组 20 80 100
中青年组 50 50 100
合 计 70 130 200
(Ⅱ) ,
所以,有99.9%的把握认为人们对此政策持支持态度支持与年龄有关.
【知识点】独立性检验
22.已知数列{a}满足a+a=12,a=6, 为 与 的等差中项.
n 1 3 2
(1)求数列{a}的通项公式;
n
(2)若数列{a}的前n项和为S ,数列{b}满足b =2S﹣a﹣1,b +b = a (a+2),求证:
n n n 2n﹣1 n n 2n 2n﹣1 n n
+…+ (n≥2).
【分析】(1)根据等差中项的概念得到数列{a}的奇数项和偶数项分别成公差为8的等差数列,再分奇偶
n
分别求出数列{a}的通项公式,即可得到结果;
n
(2)先根据等差数列的求和公式求出 S ,并根据题意求出数列{b}的通项公式,再利用数学
n n
归纳法证明不等式即可.
【解答】(1)解:∵ 为 与 的等差中项,∴ = + ,整理得:a ﹣a =
n+2 n
8,
∴a﹣a=8,又a+a=12,可解得:a=2,
3 1 1 3 1
∴数列{a}中所有的奇数项是以a=2为首项,公差为8的等差数列,
n 1
∴a =2+8(n﹣1)=8n﹣6=4(2n﹣1)﹣2,
2n﹣1
又∵a=6,∴数列{a}中所有的偶数项是以a=6为首项,公差为8的等差数列,
2 n 2
∴a =6+8(n﹣1)=8n﹣2=4×2n﹣2,
2n
综上,a=4n﹣2;
n
(2)证明:由(1)可得:S= =2n2,
n
∴b =2S﹣a﹣1=4n2﹣4n+1=(2n﹣1)2,
2n﹣1 n n
∴当n为奇数时,b=n2,
n又∵b +b = a(a+2),
2n 2n﹣1 n n
∴b =4n(2n﹣1)﹣b =4n(2n﹣1)﹣(2n﹣1)2=(2n)2﹣1,
2n 2n﹣1
∴当n为偶数时,b=n2﹣1,
n
∴b= ,
n
①当n=2时,左边=1+ = ,右边= ,不等式成立;
②假设当n=k(k≥2)时,不等式成立,即 + +…+ ≥ ﹣ ,
∵ ≥ ,
∴当n=k+1时, + +…+ + ≥ ﹣ + ,
要证当n=k+1时不等式成立,只需证 ﹣ ≥﹣ 即可,
只需证 ≥ ﹣ ,
只需证 ≥ ,
只需证k+1≤k+2,这显然成立,
故当n=k+1时不等式也成立,
综上, +…+ (n≥2).
【知识点】等差数列的性质、数列递推式