文档内容
期中检测卷 03
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.在等比数列{a}中,若a=3,a=96,则a=( )
n 4 9 1
A. B. C. D.
【答案】B
【分析】设出等比数列的公比,利用已知条件求出公比与首项即可.
【解答】解:在等比数列{a}中,若a=3,a=96,
n 4 9
设公比为q,有 ,有q=2,则 .
故选:B.
【知识点】等比数列的通项公式
2.函数 的导函数为f'(x),则f'(x)>0的解集为( )
A.(﹣∞,1) B.(0,1) C.(1,+∞) D.(0,+∞)
【答案】B
【分析】先求出函数f(x)导数,再利用f'(x)>0及函数f(x)的定义域即可解得0<x<1.
【解答】解:函数f(x)的定义域为(0,+∞),
f'(x)= ,
即 ,
解得0<x<1.
故选:B.
【知识点】利用导数研究函数的单调性
1 / 153.已知函数f(x)的定义域为R,其导函数为f'(x),f'(x)的部分图象如图所示,则( )
A.f(x)在(3,+∞)上单调递增
B.f(x)的最大值为f(1)
C.f(x)的一个极大值为f(﹣1)
D.f(x)的一个减区间为(1,3)
【答案】D
【分析】根据原函数的单调性与导函数之间的联系,结合各选项判断即可.
【解答】解:由于图象只是f'(x)的部分图象,
不能保证x (3,+∞)时,f'(x)>0恒成立,即A无法判断;
f(1)是函数f(x)的一个极大值,但不一定是最大值,即B错误;
∈
f(﹣1)是函数f(x)的一个极小值,即C错误;
当x (1,3)时,f'(x)<0,f(x)单调递减,即D正确.
故选:D.
∈
【知识点】利用导数研究函数的单调性、利用导数研究函数的极值
4.已知等差数列{a},其前n项和为S,若a+a=12,S=S,则S 的最大值为( )
n n 3 4 3 9 n
A.12 B.24 C.36 D.48
【答案】C
【分析】利用等差数列通项公式求出a=11,d=﹣2,求出等差数列的前n项和,由此能求出S 的最大值.
1 n
【解答】解:∵等差数列{a},其前n项和为S,a+a=12,S=S,
n n 3 4 3 9
∴ ,
解得a=11,d=﹣2,
1
∴S= =﹣(n﹣6)2+36.
n
∴n=6时,S 取最大值36.
n
故选:C.
【知识点】等差数列的性质
2 / 155.在《九章算术》中有一个古典名题“两鼠穿墙”问题:今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠
也日一尺,大鼠日自倍,小鼠日自半.大意是有两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一
尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.若垣厚 33 尺,则两鼠几日可相逢
( )
A.5 B.6 C.7 D.8
【答案】B
【分析】根据具体大老鼠和小老鼠打洞的数值构成两个等比数列,利用等比数列的求和公式进行求解即可.
【解答】解:大老鼠打洞构成首项为1,公比为2的等比数列,
小老鼠打洞构成首项为1,公比为 的等比数列,
设相遇时是第n天,
则满足 + ≥33,
即2n﹣1+2﹣ ≥33,
即2n﹣ ≥32,
则f(n)=2n﹣ 在n≥1上是增函数,
∵f(5)=25﹣ =32﹣ <32,
f(6)=26﹣ =64﹣ >32,
∴相遇时是第6天,
故选:B.
【知识点】等比数列的前n项和
6.已知函数f(x)= ,若对任意x >x >0,f(x )>f(x )恒成立,则a的取值范围
1 2 1 2
为( )
A.[1,+∞) B.(﹣∞,1] C.[e,+∞) D.[1,e]
3 / 15【答案】A
【分析】求出函数的导数,问题转化为 在(0,+∞)上恒成立,令 ,根据函数的
单调性求出a的取值范围即可.
【解答】解:由题意知函数f(x)在(0,+∞)上单调递增,
因为f′(x)=ax﹣lnx﹣1,所以转化为f′(x)≥0在(0,+∞)上恒成立,
因为x (0,+∞),所以 在(0,+∞)上恒成立,
∈
即转化为 ,令 ,则 ,
所以当x (0,1)时,g′(x)>0,当x (1,+∞)时,g′(x)<0,
所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∈ ∈
所以g(x) =g(1)=1,所以a≥1,
max
故选:A.
【知识点】利用导数研究函数的最值
7.已知定义在(0,+∞)上的函数f(x),恒为正数的f(x)符合f(x)<f′(x)<2f(x),则 的
取值范围为( )
A.(e,2e) B. C.(e,e3) D.
【答案】D
【分析】分别构造函数g(x)= ,x (0,+∞),h(x)= ,x (0,+∞),利用导数研究
∈ ∈
其单调性即可得出.
【解答】解:令g(x)= ,x (0,+∞),
∈
∵∀x (0,+∞),f(x)<f′(x),
∈
∴g′(x)= = >0,
∴g(x)= 在区间(0,+∞)上单调递增,
4 / 15∴g(1)= < =g(2),
∴ < ①;
再令h(x)= ,x (0,+∞),
∈
∵∀x (0,+∞),f′(x)<2f(x)恒成立,
∈
∴h′(x)= = <0,
∴函数h(x)在x (0,+∞)上单调递减,
∈
∴h(1)= > =h(2),
∴ > ②,
综上①②可得: < < .
故选:D.
【知识点】利用导数研究函数的单调性
8.已知数集 S={a ,a ,a ,…,a}(1≤a <a <…<a ,n≥2)具有性质 P:对任意的 i,j
1 2 3 n 1 2 n
(1≤i≤j≤n),aa S或 ∈S成立,则( )
i j
∈
A.若n=3,则a,a,a 成等差数列
1 2 3
B.若n=4,则a,a,a,a 成等比数列
1 2 3 4
C.若n=5,则a,a,a,a,a 成等差数列
1 2 3 4 5
D.若n=7,则a,a,a,a,a,a,a 成等比数列
1 2 3 4 5 6 7
【答案】D
【分析】取特殊的数集,由性质P,符合条件,但是不符合A,B,C,故选D.
【解答】解:A:n=3时,取数集S={1,2,4},也有对任意的i,j(1≤i≤j≤3), ∈S成立,但
a,a,a 不成等差数列,所以A不正确;
1 2 3
5 / 15B:n=4时,取数集S={1,2,3,6},也有对任意的i,j(1≤i≤j≤4), ∈S成立,但
a,a,a,a 不成等比数列,所以B不正确;
1 2 3 4
C:n=5,取数集S={1,2,4,8,16},也有对任意的i,j(1≤i≤j≤5), ∈S成立,但
a,a,a,a,a 不成等差数列,所以C不正确;
1 2 3 4 5
故选:D.
【知识点】等比数列的性质
二、多选题(本大题共4小题,每小题5分,共20分)在每小题所给出的四个选项中,有多项是符合题目
要求的;错选或多选不得分。
9.以下四个式子分别是函数在其定义域内求导,其中正确的是( )
A.( )′= B.(cos2x)'=﹣2sin2x
C. D.(lgx)′=
【答案】BC
【分析】根据基本初等函数和复合函数的求导公式对每个选项函数进行求导即可.
【解答】解: ,(cos2x)′=﹣2sin2x, , .
故选:BC.
【知识点】导数的运算
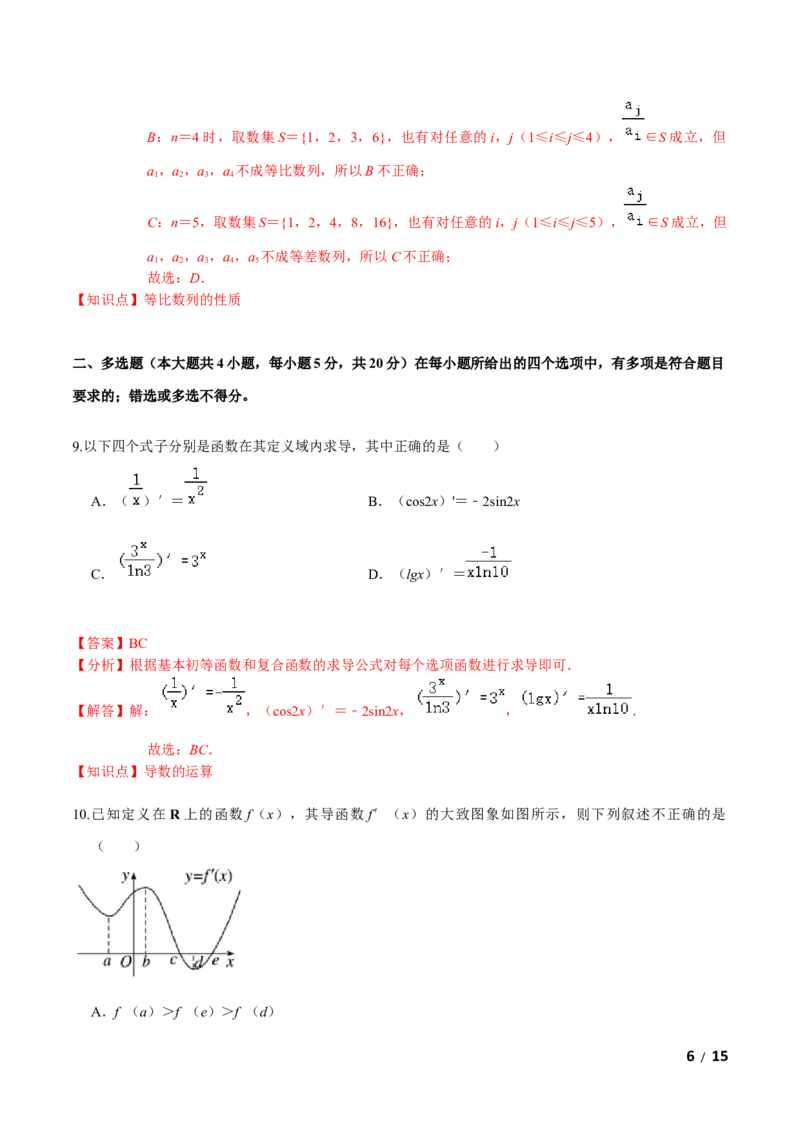
10.已知定义在 R上的函数 f(x),其导函数 f′(x)的大致图象如图所示,则下列叙述不正确的是
( )
A.f (a)>f (e)>f (d)
6 / 15B.函数f (x)在[a,b]上递增,在[b,d]上递减
C.函数f (x)的极值点为c,e
D.函数f (x)的极大值为f (b)
【答案】ABD
【分析】根据导数与函数单调性的关系及所给图象可得f(x)的单调性,判断函数的极值即可.
【解答】解:由导数与函数单调性的关系知,当f′(x)>0时f(x)递增,f′(x)<0时f(x)递减,
结合所给图象知,x (a,c)时,f′(x)>0,
∴f(x)在(a,c)上单调递增,
∈
x (c,e)时,f′(x)<0,
∴f(x)在(c,e)上单调递减,
∈
函数f(x)在x=c处取得极大值,在x=e处取得极小值;
f(c)>f(e),
故选:ABD.
【知识点】利用导数研究函数的单调性、函数的图象与图象的变换
11.无穷数列{a}的前n项和S=an2+bn+c,其中a,b,c为实数,则( )
n n
A.{a}可能为等差数列
n
B.{a}可能为等比数列
n
C.{a}中一定存在连续三项构成等差数列
n
D.{a}中一定存在连续三项构成等比数列
n
【答案】ABC
【分析】先由题设求得数列{a}的通项公式a ,再根据等差、等比数列的定义与性质利用特值法逐个选项
n n
判断正误即可.
【解答】解:由S =an2+bn+c可得:S =a(n﹣1)2+b(n﹣1)+c(n≥2),两式相减整理得:a =
n n﹣1 n
2an+b﹣a,n≥2,
又当n=1时,有a=S=a+b+c,
1 1
∴a= ,
n
当a=c=0,b=1时,a=1,此时数列{a}既是等差数列,又是等比数列,故选项A、B正确;
n n
又a=3a+b,a=5a+b,a=7a+b,2a=a+a,此时a,a,a 成等差数列,故选项C正确;
2 3 4 3 2 4 2 3 4
当a=b=c=0时,a=0,此时数列{a}中不存在连续三项构成等比数列,故选项D错误,
n n
故选:ABC.
【知识点】等比数列的性质、等差数列的性质
12.等比数列{a}中,公比为q,其前n项积为T,并且满足a>1.a •a ﹣1>0, <0,下列选项
n n 1 99 100
7 / 15中,正确的结论有( )
A.0<q<1
B.a •a ﹣1<0
99 101
C.T 的值是T 中最大的
100 n
D.使T>1成立的最大自然数n等于198
n
【答案】ABD
【分析】由已知a a ﹣1>0,得q>0,再由 <0得到q<1说明A正确;再由等比数列的性质结
99 100
合a <1说明B正确;由T =T •a ,而0<a <1,求得 T <T ,说明C错误;分别求得
100 100 99 100 100 100 99
T >1,T <1说明D正确.
198 199
【解答】解:对于A,∵a a ﹣1>0,∴a2•q197>1,∴(a•q98)2•q>1.
99 100 1 1
∵a>1,∴q>0.
1
又∵ <0,∴a >1,且a <1 .
99 100
∴0<q<1,故A正确;
对于B,∵ ,∴0<a •a <1,即 a •a ﹣1<0,故B正确;
99 101 99 101
对于C,由于T =T •a ,而0<a <1,故有 T <T ,故C错误;
100 99 100 100 100 99
对于D,T =a•a…a =(a•a )(a•a )…(a •a )=(a •a )×99>1,
198 1 2 198 1 198 2 197 99 100 99 100
T =a•a…a =(a•a )(a•a )…(a •a )•a <1,故D正确.
199 1 2 199 1 199 2 198 99 101 100
∴不正确的是C.
故选:ABD.
【知识点】等比数列的前n项和
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.已知数列{a}是公比为2的等比数列,其前n项和为S,且S﹣2S=1,则a+a= .
n n 7 6 1 5
【答案】17
【分析】直接利用等比数列的通项公式和前n项和的公式的应用求出结果.
【解答】解:数列{a}是公比为2的等比数列,其前n项和为S,且S﹣2S=1,
n n 7 6
所以 ,解得a=1,
1
故a+a=1+16=17.
1 5
故答案为:17.
8 / 15【知识点】等比数列的前n项和
14.设等差数列{a}的各项都是正数,公差为d,前n项和为S ,若数列 也是公差为d的等差数列,
n n
则{a}的前6项和为 .
n
【分析】由题意可得,化简,n≠1时可得:a=(n﹣1)d2+2 d﹣ d.分别令n=2,3,解得即可.
1
【解答】解:由题意可得:S =na+ d.a >0. = +(n﹣1)d,可得:S =a+(n﹣1)
n 1 n n 1
2d2+2 (n﹣1)d.
∴na+ d=a+(n﹣1)2d2+2 (n﹣1)d.
1 1
n≠1时可得:a=(n﹣1)d2+2 d﹣ d.
1
分别令n=2,3,可得:a=d2+2 d﹣d,a=2d2+2 d﹣ d.
1 1
解得a= ,d= .
1
∴S=6× + ×5×6= .
6
故答案为:
【知识点】等差数列的前n项和
15.规定 ,其中x R,m N*,且 ,这是排列数 (n,m N*,且m≤n)的
∈ ∈ ∈
一种推广.则 = ,则函数 的单调减区间为 .
【分析】直接由排列数公式展开求得 ;展开排列数公式,得到f(x)的解析式,求出导函数,再由
导数小于0求得函数的单调减区间.
【解答】解:由 ,
得 = = ;
函数 =x(x﹣1)(x﹣3+1)=x3﹣3x2+2x,
∴f′(x)=3x2﹣6x+2.
9 / 15由f′(x)<0,得3x2﹣6x+2<0,解得 <x< .
∴函数 的单调减区间为( , ).
故答案为: ;( , ).
【知识点】利用导数研究函数的单调性、排列及排列数公式
16.已知函数f(x)=lgx,g(x)=x3+3ax2+a+6,若存在x >0,x >0,x≠x ,使得f(g(x ))=f(g
1 2 1 2 1
(x))<0,则a的取值范围是 ﹣ ﹣ .
2
【答案】(-6,-1)
【分析】依题意,函数 g(x)的图象与函数y=k(0<k<1)在(0,+∞)上存在两个交点,对函数 g
(x)求导,可知a必然小于0,且满足 ,解出即可.
【解答】解:函数f(x)=lgx的定义域为{x|x>0},且为单调函数,当x (0,1)时,f(x)<0,
∈
故存在x>0,x>0,x≠x,使得 ,即函数g(x)的图象与函数y=k(0<k
1 2 1 2
<1)在(0,+∞)上存在两个交点,
g′(x)=3x2+6ax=3x(x+2a),令g′(x)=0,解得x=0或x=﹣2a,
若a≥0,则g′(x)≥0在(0,+∞)上恒成立,函数g(x)在(0,+∞)上单调递增,
此时不可能满足g(x)的图象与函数y=k(0<k<1)在(0,+∞)上有两个交点,故a<0,
此时只需满足 即可,即 ,解得﹣6<a<﹣1,
综上,实数a的取值范围为(﹣6,﹣1).
故答案为:(﹣6,﹣1).
【知识点】利用导数研究函数的最值
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.已知函数f(x)=xex+a(x+1)2(a R).
(1)若a=﹣1,求f′(x)的单调区间∈ ;
(2)若a>0,证明f(x)有且仅有两个零点.
【分析】(1)若a=﹣1,则f(x)=xex﹣(x+1)2,求f′(x)=xex+ex﹣2(x+1)=(x+1)(ex﹣
2),令h(x)=f′(x)=(x+1)(ex﹣2),h′(x)=(x+2)ex﹣2,令p(x)=h′(x)
10 / 15=(x+2)ex﹣2
p′(x)=(x+3)ex,当x (﹣3,+∞)时,p′(x)>0,p(x)单调递增,且p(x)<
0,当x (﹣∞,﹣3)时,p′(x)<0,p(x)单调递减,且p(0)=0 p(x) =p(﹣
min
∈
3)=﹣e﹣3﹣2<0,就可求出答案.
∈
(2)f′(x)=(x+1)(ex+2a),得出单调区间进而得出最小值f(﹣1)=﹣e﹣1<0,又f
(0)=a>0,f(2)=2e2+9a>0,即可证明.
【解答】解:(1)若a=﹣1,则f(x)=xex﹣(x+1)2,
定义域为R,
∴f′(x)=xex+ex﹣2(x+1)=(x+1)(ex﹣2),
令h(x)=f′(x)=(x+1)(ex﹣2),
h′(x)=(x+2)ex﹣2,
令p(x)=h′(x)=(x+2)ex﹣2,
p′(x)=(x+3)ex,
当x (﹣3,+∞)时,p′(x)>0,p(x)单调递增,且p(0)=0,
当x (﹣3,0)时,p(x)<0,当x (0,+∞)时,p(x)>0,
∈
当x (﹣∞,﹣3)时,p′(x)<0,p(x)单调递减,且p(x)<0,
∈ ∈
p(x) =p(﹣3)=﹣e﹣3﹣2<0,
min
∈
∴当x (0,+∞),p(x)>0,h′(x)>0,h(x)单调递增,即f′(x)单调递增,
当x (﹣∞,0),p(x)<0,h′(x)<0,h(x)单调递减,即f′(x)单调递减,
∈
(2)若a>0,f′(x)=(x+1)(ex+2a),
∈
∴在区间(﹣1,+∞) 上,f′(x)>0,f(x) 单调递增,
在区间(﹣∞,﹣1)上,f′(x)<0,f(x)单调递减,
f(x) =f(﹣1)=﹣e﹣1<0
min
f(0)=a>0,记x=﹣1﹣ <﹣1,
0
由y=xex在(﹣∞,﹣1)上单调递减知xe >﹣ ,∴f(x)=xe +1>﹣
0 0 0
所以f(x)有且仅有两个零点.,
【知识点】利用导数研究函数的单调性
18.已知等差数列{a}的前n项和为S,且a=﹣5,S=﹣20.
n n 2 5
(1)求数列{a}的通项公式;
n
(2)求S 取得最小值时n的取值.
n
【分析】(1)设出等差数列的首项和公差,由题意列式求出首项和公差,则等差数列的通项公式可求;
(2)写出等差数列的前n项和,利用配方法求得S 的最小值并求得使S 取得最小值时n的取值.
n n
【解答】解:(1)设等差数列{a}的首项为a,公差为d,
n 1
由a=﹣5,S=﹣20,得 ,即 .
2 5
∴a=﹣6+1×(n﹣1)=n﹣7;
n
11 / 15(2) = ,
∴当n=6或7时,S 取得最小值.
n
【知识点】等差数列的前n项和
19.已知等差数列{a}的前n项和为S,a+a=12,S=16.
n n 2 5 4
(1)求{a}的通项公式;
n
(2)数列{b}满足b = 为数列{b}的前n项和,是否存在正整数m,k(1<m<k),使得T
n n n k
=3T 2?若存在,求出m,k的值;若不存在,请说明理由.
m
【分析】(1)设等差数列{a}的公差为d,利用已知条件列出方程求解首项与公差,得到通项公式.
n
(2)求出 ,化简{b}的通项公式,利用裂项消项法求和,通过
n
,分析求解即可.
【解答】解:(1)设等差数列{a}的公差为d,
n
由 ,
解得 ∴ .
(2) ,
∴ .
∴T=b+b+…+b=
n 1 2 n
= = .
若 ,则
整理得 ,
12 / 15又k>m>1∴
整理得
解得 ,
又m N*
∴m=2,∴k=12.
∈
∴存在m=2,k=12满足题意.
【知识点】数列的求和、等差数列的通项公式
20.已知函数 ,且f(x)不恒为0.
(1)若f(x)为奇函数,求实数a的值;
(2)若g(x)=ef(x),且函数g(x)在(0,1)上单调递减,求实数a的取值范围.
【分析】(1)根据函数的奇偶性求出a的值即可;(2)求出g(x)的解析式,求出函数的导数,根据函
数的单调性得到关于a的不等式,解出即可.
【解答】解:(1)若f(x)为奇函数,则f(﹣x)=﹣f(x),
则 = ,故a2=1,解得:a=±1,
a=1时,f(x)=ln1=0,f(x)恒为0,不合题意,
a=﹣1时,f(x)=ln ,符合题意,
故a=﹣1;
(2)若g(x)=ef(x)= =a+ ,
∵g(x)在(0,1)上单调递减,
∴g′(x)=(2﹣2a)(﹣ )<0,
∴2﹣2a>0,故a<1,
故a的取值范围是(﹣∞,1).
【知识点】函数奇偶性的性质与判断、利用导数研究函数的单调性
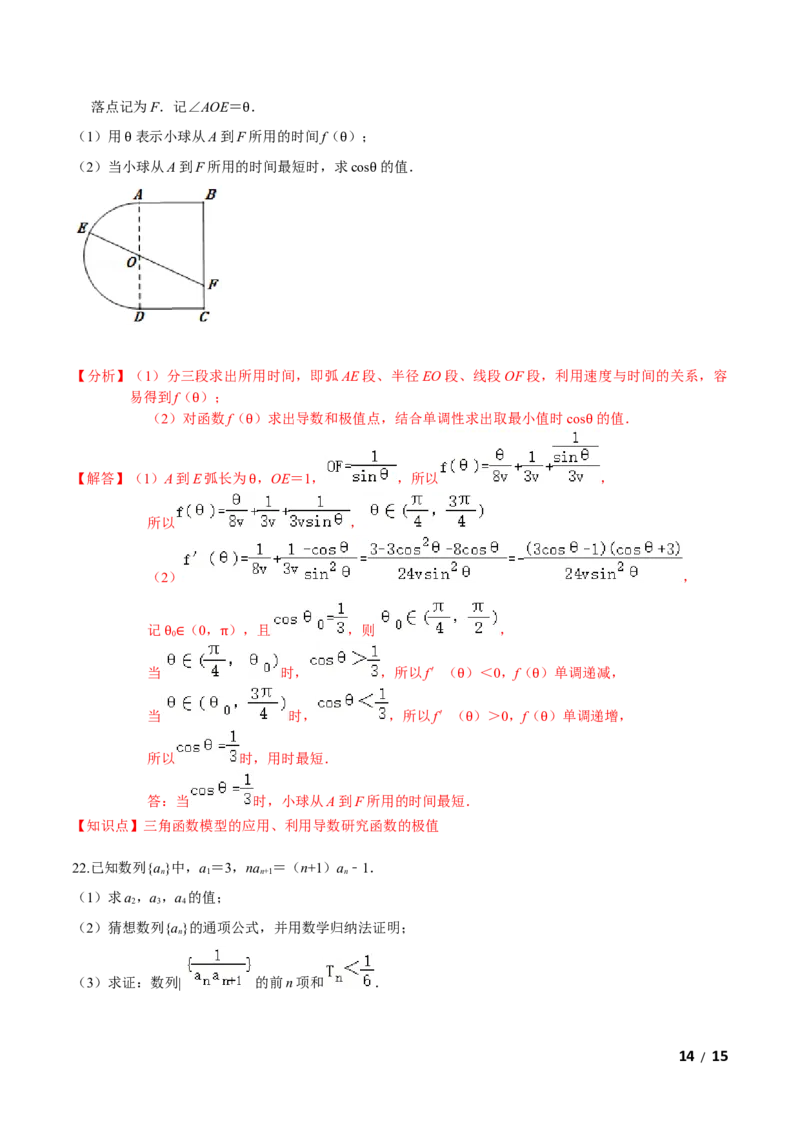
21.一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发
以8v的速度沿半圆O轨道滚到某点E处后,以3v的速度沿与点E切线垂直的方向弹射到落袋区BC内,
13 / 15落点记为F.记∠AOE= .
(1)用 表示小球从A到Fθ所用的时间f( );
(2)当小θ球从A到F所用的时间最短时,求θcos 的值.
θ
【分析】(1)分三段求出所用时间,即弧AE段、半径EO段、线段OF段,利用速度与时间的关系,容
易得到f( );
(2)对函数f( )求出导数和极值点,结合单调性求出取最小值时cos 的值.
θ
θ θ
【解答】(1)A到E弧长为 ,OE=1, ,所以 ,
θ
所以 ,
(2) ,
记 (0, ),且 ,则 ,
0
θ∈ π
当 时, ,所以f′( )<0,f( )单调递减,
θ θ
当 时, ,所以f′( )>0,f( )单调递增,
θ θ
所以 时,用时最短.
答:当 时,小球从A到F所用的时间最短.
【知识点】三角函数模型的应用、利用导数研究函数的极值
22.已知数列{a}中,a=3,na =(n+1)a﹣1.
n 1 n+1 n
(1)求a,a,a 的值;
2 3 4
(2)猜想数列{a}的通项公式,并用数学归纳法证明;
n
(3)求证:数列| 的前n项和 .
14 / 15【分析】(1)由题意可得 ,分别令n=1,2,3,代入计算可得所求值;
(2)猜想a =2n+1,n N*.运用数学归纳法证明,注意首先验证n=1成立,再假设当n=k
n
(k N*)时,等式成立,运用已知数列的递推式,化简整理可得n=k+1时,等式也成立,即
∈
可得证;
∈
(3)可令 ,运用数列的裂项相消求和和
不等式的性质,即可得证.
【解答】解:(1)由已知得, ,又a=3,
1
所以a=2a﹣1=5,a= a﹣ =7,a= a﹣ =9;
2 1 3 2 4 3
(2)猜想a=2n+1,n N*.
n
证明:①当n=1时,a=3,等式成立;
1
∈
②假设当n=k(k N*)时,等式成立,即a=2k+1,
k
∈
当n=k+1时, .
∴n=k+1时,等式成立.
由①②可知,a=2n+,(n N*成立;
n
∈
(3)证明:令 ,
T=b+b+…+b +b=
n 1 2 n﹣1 n
= ,即 .
【知识点】数学归纳法、数列的求和
15 / 15