文档内容
期中检测卷 04
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.已知直线a在平面 外,则( )
A.a∥ α
B.直线αa与平面 至少有一个公共点
C.a∩ =A α
D.直线αa与平面 至多有一个公共点
α
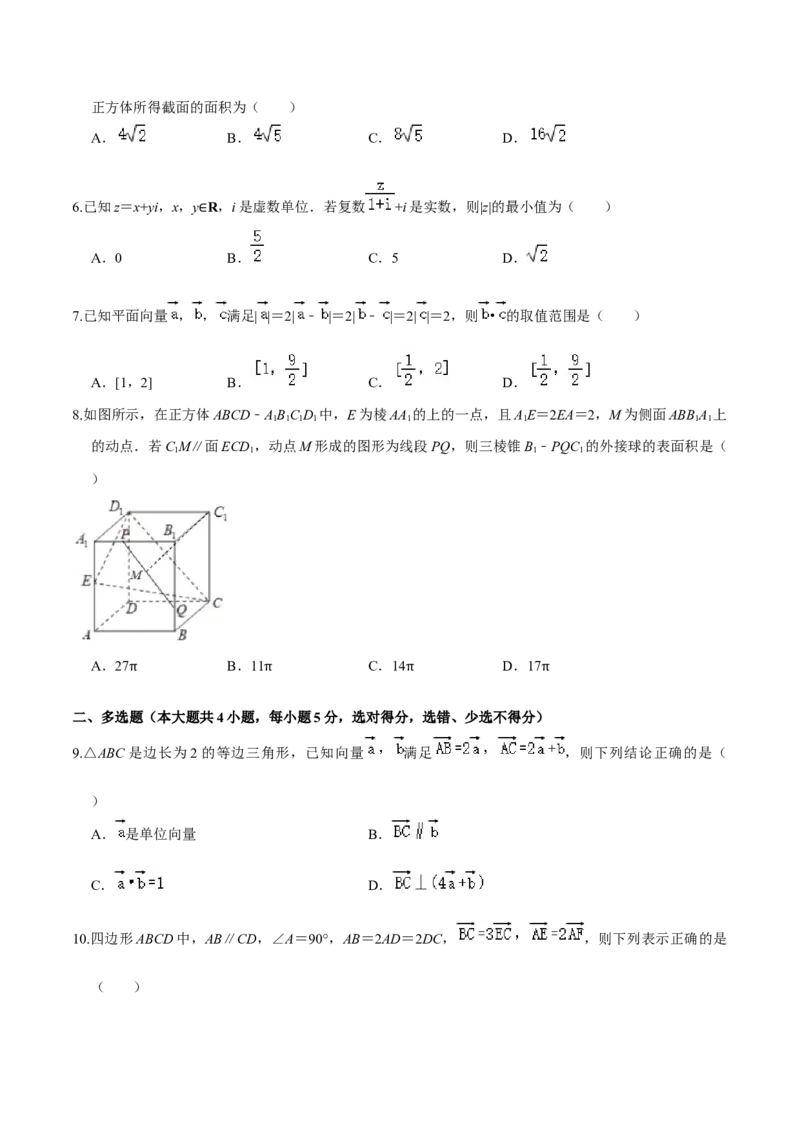
2.在△ABC中, , .若点D满足 ,则 =( )
A. B. C. D.
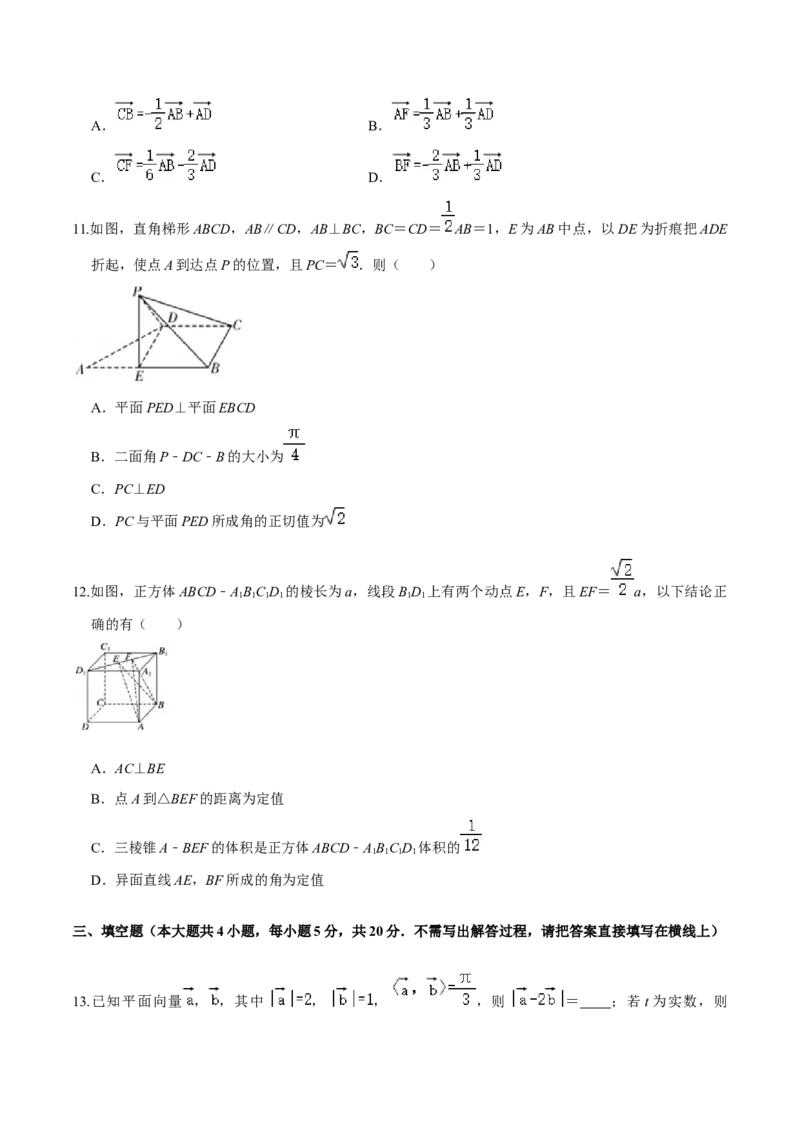
3.设E为△ABC所在平面内一点,若 =2 ,则( )
A. = + B. = ﹣
C. = + D. = ﹣
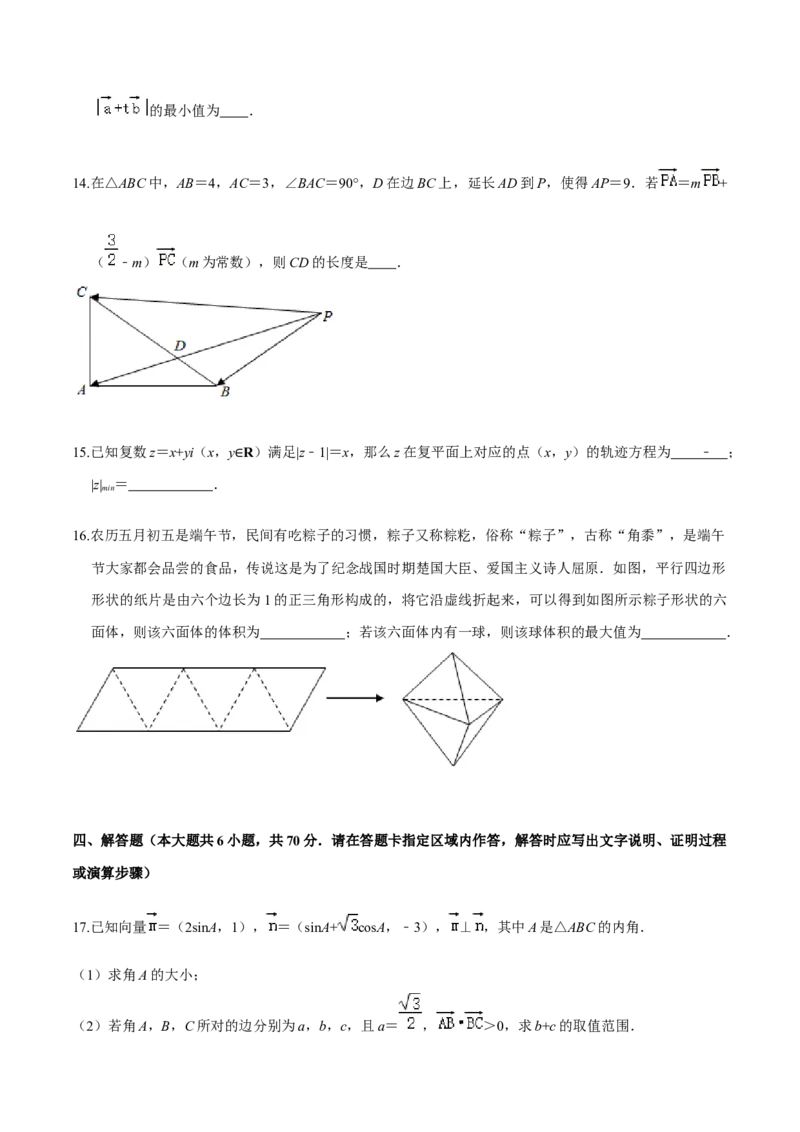
4.复数z满足z(1+i)=1﹣ai,且z在复平面内对应的点在第四象限,则实数a的取值范围是( )
A.[﹣1,1] B.(﹣∞,﹣1) C.(﹣1,1) D.(1,+∞)
5.在棱长为4的正方体ABCD﹣ABC D 中,点M为BC 的中点,过点D作平面a使a⊥BM,则平面a截
1 1 1 1 1 1正方体所得截面的面积为( )
A. B. C. D.
6.已知z=x+yi,x,y R,i是虚数单位.若复数 +i是实数,则|z|的最小值为( )
∈
A.0 B. C.5 D.
7.已知平面向量 , , 满足| |=2| ﹣ |=2| ﹣ |=2| |=2,则 • 的取值范围是( )
A.[1,2] B. C. D.
8.如图所示,在正方体ABCD﹣ABC D 中,E为棱AA 的上的一点,且AE=2EA=2,M为侧面ABBA 上
1 1 1 1 1 1 1 1
的动点.若C M∥面ECD ,动点M形成的图形为线段PQ,则三棱锥B﹣PQC 的外接球的表面积是(
1 1 1 1
)
A.27 B.11 C.14 D.17
π π π π
二、多选题(本大题共4小题,每小题5分,选对得分,选错、少选不得分)
9.△ABC是边长为2的等边三角形,已知向量 满足 ,则下列结论正确的是(
)
A. 是单位向量 B.
C. D.
10.四边形ABCD中,AB∥CD,∠A=90°,AB=2AD=2DC, ,则下列表示正确的是
( )A. B.
C. D.
11.如图,直角梯形ABCD,AB∥CD,AB⊥BC,BC=CD= AB=1,E为AB中点,以DE为折痕把ADE
折起,使点A到达点P的位置,且PC= .则( )
A.平面PED⊥平面EBCD
B.二面角P﹣DC﹣B的大小为
C.PC⊥ED
D.PC与平面PED所成角的正切值为
12.如图,正方体ABCD﹣ABC D 的棱长为a,线段BD 上有两个动点E,F,且EF= a,以下结论正
1 1 1 1 1 1
确的有( )
A.AC⊥BE
B.点A到△BEF的距离为定值
C.三棱锥A﹣BEF的体积是正方体ABCD﹣ABC D 体积的
1 1 1 1
D.异面直线AE,BF所成的角为定值
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.已知平面向量 , ,其中 , , ,则 = ;若 t为实数,则的最小值为 .
14.在△ABC中,AB=4,AC=3,∠BAC=90°,D在边BC上,延长AD到P,使得AP=9.若 =m +
( ﹣m) (m为常数),则CD的长度是 .
15.已知复数z=x+yi(x,y R)满足|z﹣1|=x,那么z在复平面上对应的点(x,y)的轨迹方程为 ﹣ ;
|z| = . ∈
min
16.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午
节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形
形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六
面体,则该六面体的体积为 ;若该六面体内有一球,则该球体积的最大值为 .
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.已知向量 =(2sinA,1), =(sinA+ cosA,﹣3), ⊥ ,其中A是△ABC的内角.
(1)求角A的大小;
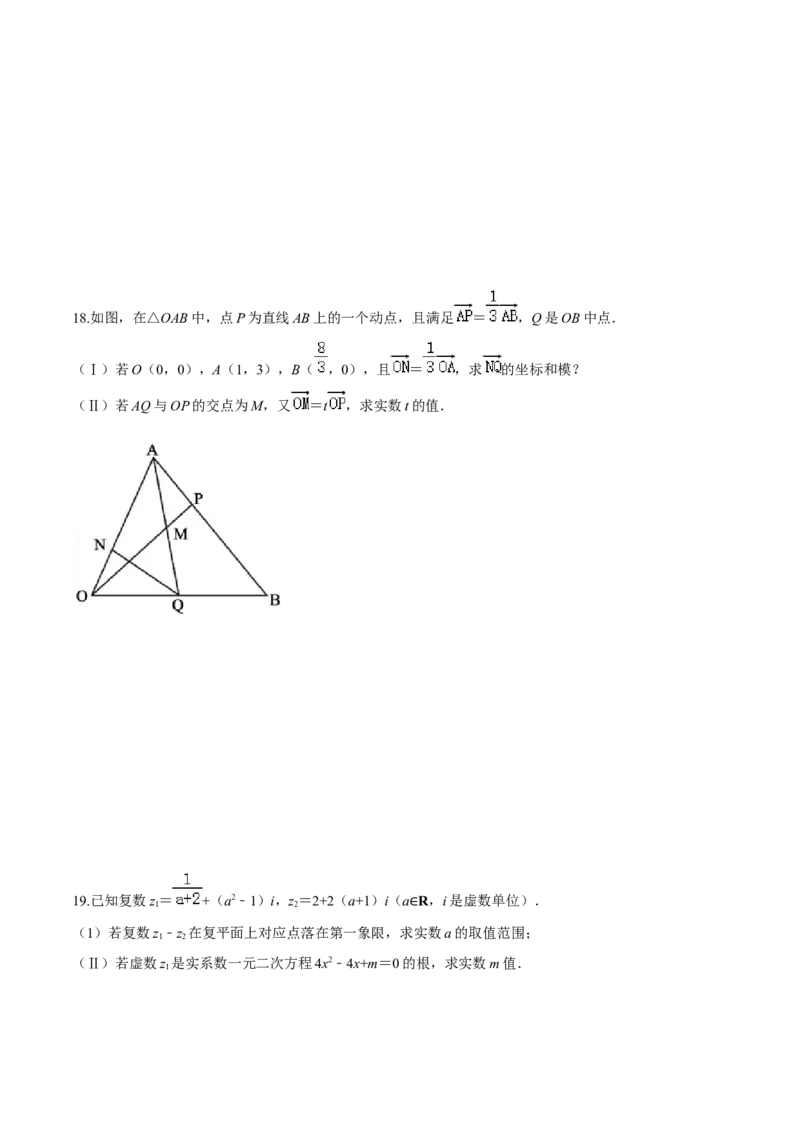
(2)若角A,B,C所对的边分别为a,b,c,且a= , >0,求b+c的取值范围.18.如图,在△OAB中,点P为直线AB上的一个动点,且满足 = ,Q是OB中点.
(Ⅰ)若O(0,0),A(1,3),B( ,0),且 = ,求 的坐标和模?
(Ⅱ)若AQ与OP的交点为M,又 =t ,求实数t的值.
19.已知复数z= +(a2﹣1)i,z=2+2(a+1)i(a R,i是虚数单位).
1 2
(1)若复数z﹣z 在复平面上对应点落在第一象限,求∈实数a的取值范围;
1 2
(Ⅱ)若虚数z 是实系数一元二次方程4x2﹣4x+m=0的根,求实数m值.
120.已知复数z满足z=(﹣1+3i)(1﹣i)﹣4.
(1)求复数z的共轭复数;
(2)若 =z+ai,且复数 对应向量的模不大于复数z所对应向量的模,求实数a的取值范围.
ω ω
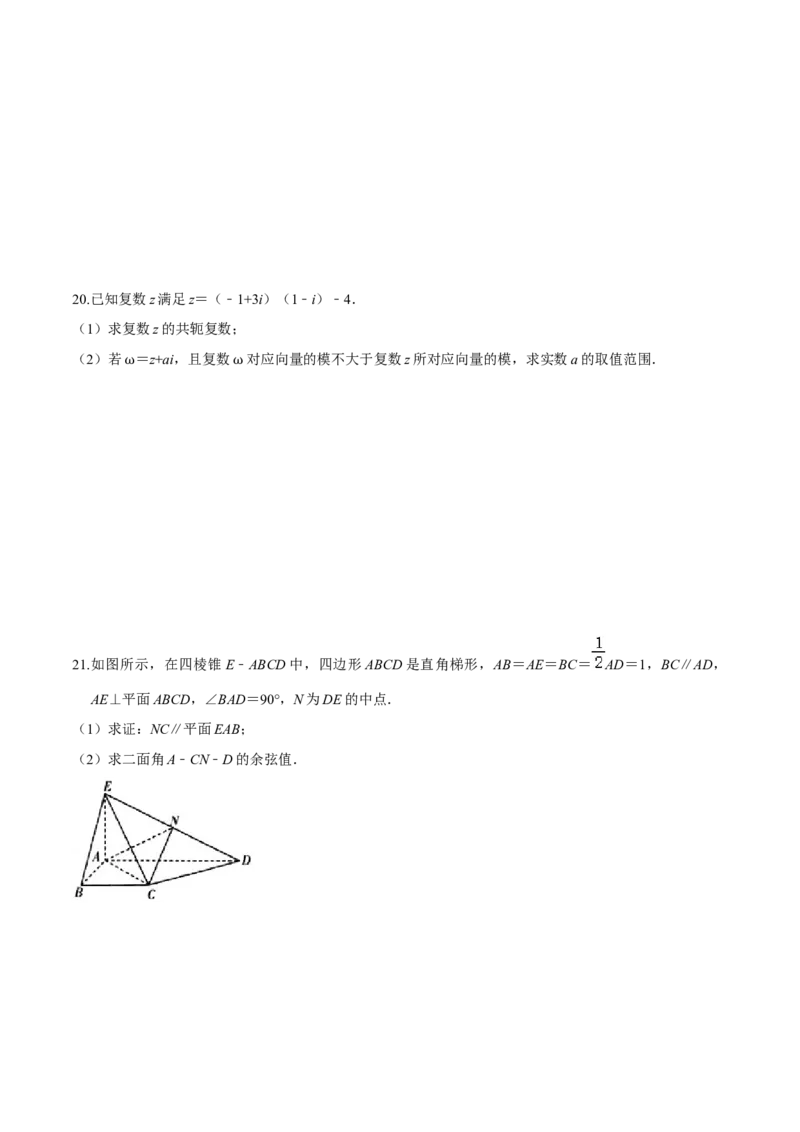
21.如图所示,在四棱锥E﹣ABCD中,四边形ABCD是直角梯形,AB=AE=BC= AD=1,BC∥AD,
AE⊥平面ABCD,∠BAD=90°,N为DE的中点.
(1)求证:NC∥平面EAB;
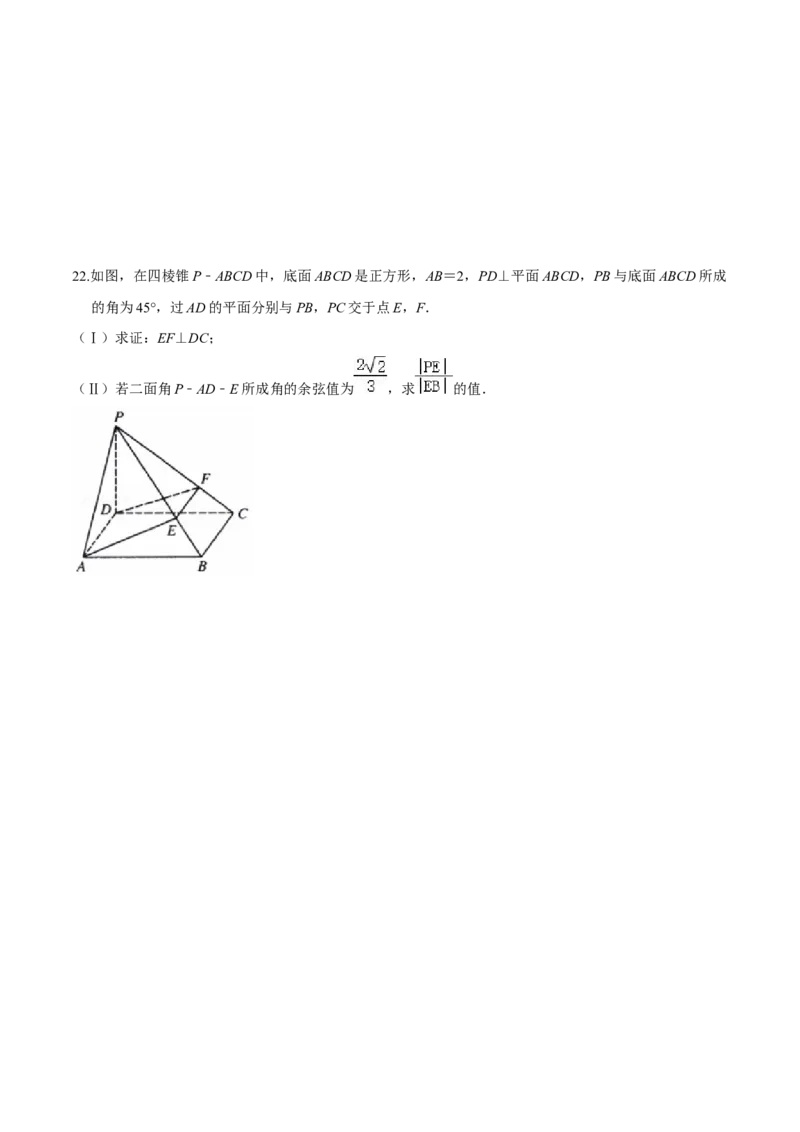
(2)求二面角A﹣CN﹣D的余弦值.22.如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,AB=2,PD⊥平面ABCD,PB与底面ABCD所成
的角为45°,过AD的平面分别与PB,PC交于点E,F.
(Ⅰ)求证:EF⊥DC;
(Ⅱ)若二面角P﹣AD﹣E所成角的余弦值为 ,求 的值.