文档内容
期中检测卷 05
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
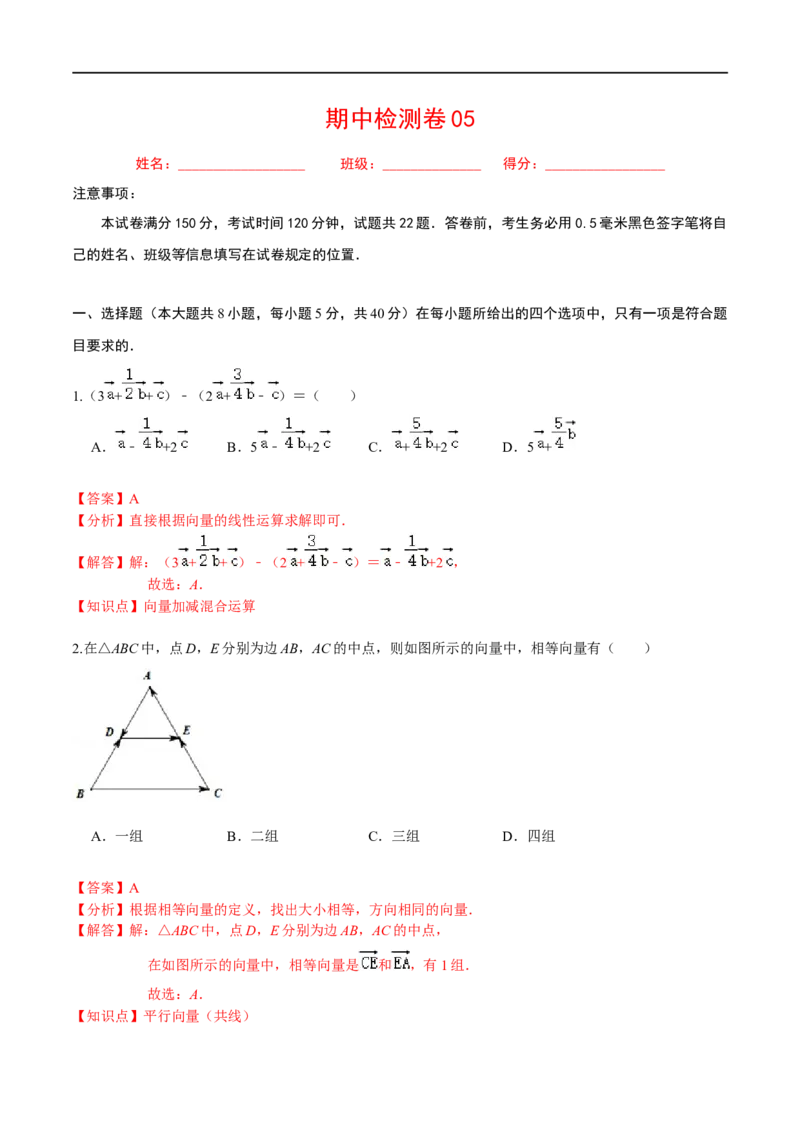
1.(3 + + )﹣(2 + ﹣ )=( )
A. ﹣ +2 B.5 ﹣ +2 C. + +2 D.5 +
【答案】A
【分析】直接根据向量的线性运算求解即可.
【解答】解:(3 + + )﹣(2 + ﹣ )= ﹣ +2 ,
故选:A.
【知识点】向量加减混合运算
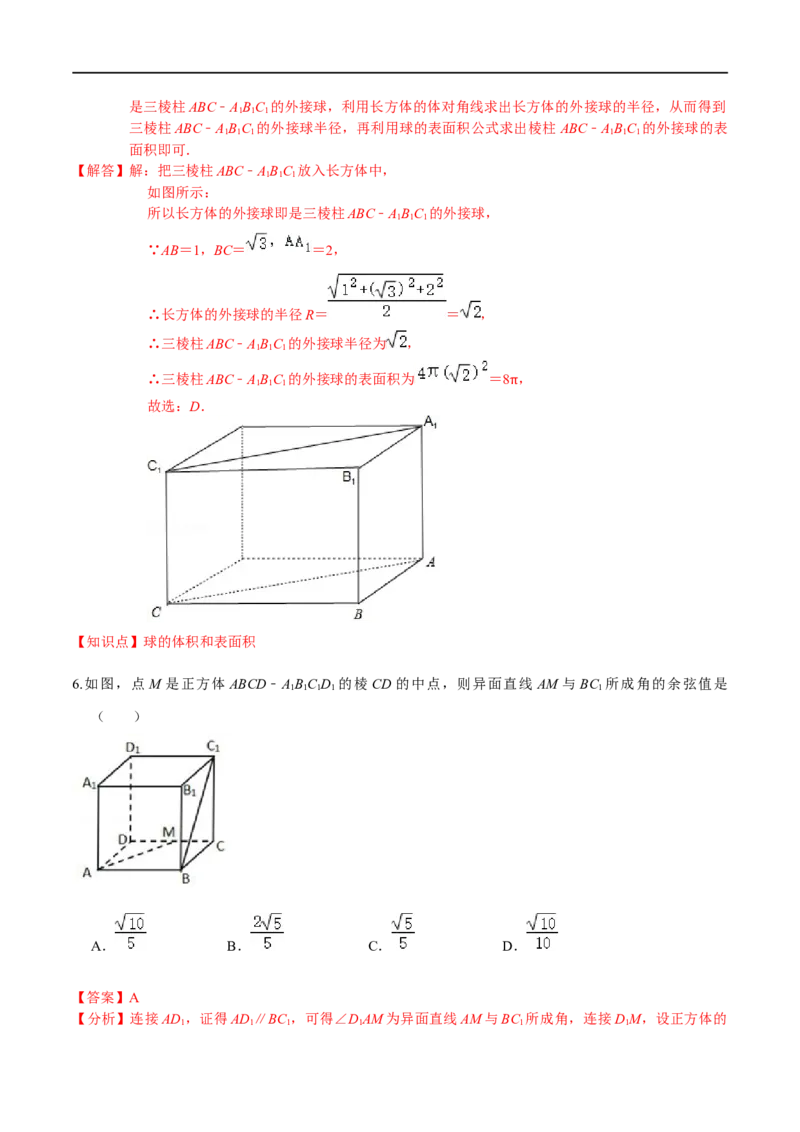
2.在△ABC中,点D,E分别为边AB,AC的中点,则如图所示的向量中,相等向量有( )
A.一组 B.二组 C.三组 D.四组
【答案】A
【分析】根据相等向量的定义,找出大小相等,方向相同的向量.
【解答】解:△ABC中,点D,E分别为边AB,AC的中点,
在如图所示的向量中,相等向量是 和 ,有1组.
故选:A.
【知识点】平行向量(共线)3.设i为虚数单位,复数z满足z(1﹣i)=2i,则|z|=( )
A.1 B. C.2 D.2
【答案】B
【分析】把已知等式变形,利用复数代数形式的乘除运算,再由复数模的计算公式求解.
【解答】解:由z(1﹣i)=2i,得z= ,
∴|z|= .
故选:B.
【知识点】复数的模
4.已知复数z=(1+i)(a﹣i)在复平面内对应的点位于第四象限,则实数a的取值范围是( )
A.(1,+∞) B.(﹣∞,﹣1) C.(﹣∞,1) D.(﹣1,1)
【答案】D
【分析】根据复数的运算性质、几何意义即可得出.
【解答】解:复数z=(1+i)(a﹣i)=a+1+(a﹣1)i在复平面内对应的点位于第四象限,
∴a+1>0,a﹣1<0.
解得﹣1<a<1.
则实数a的取值范围是(﹣1,1).
故选:D.
【知识点】复数的代数表示法及其几何意义
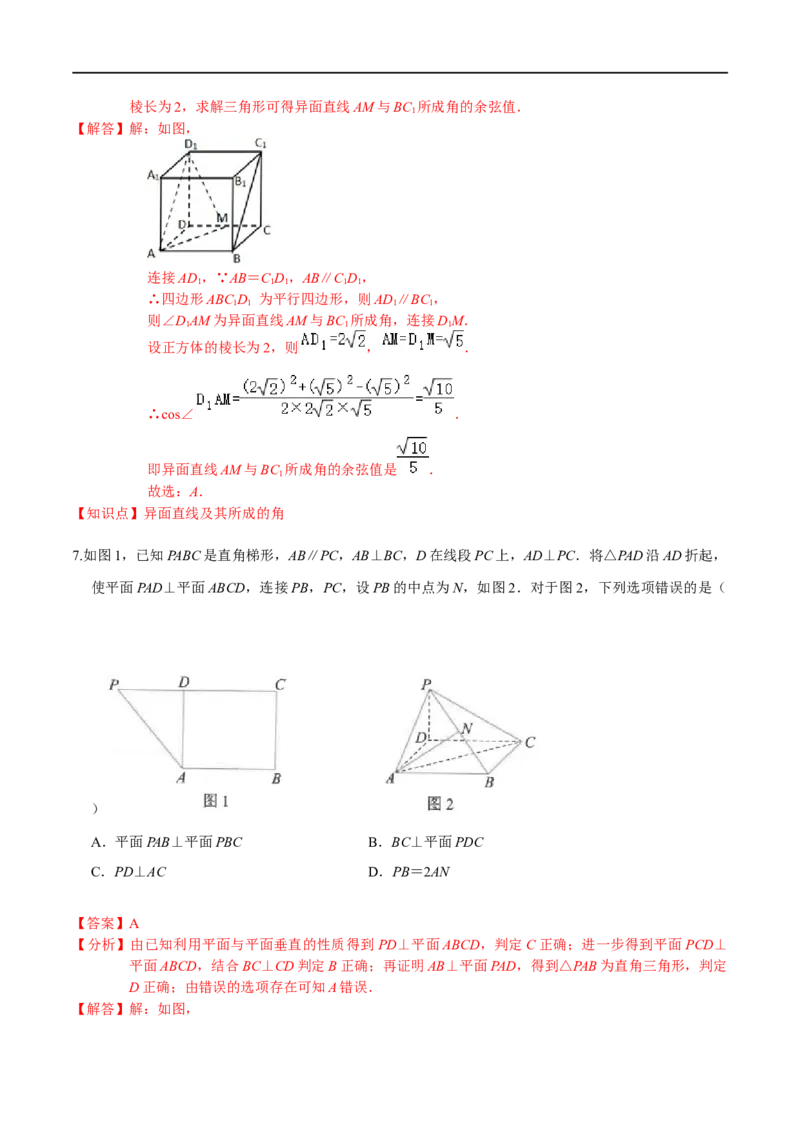
5.三棱柱ABC﹣ABC 中,AA⊥平面ABC,∠ABC=90°,AB=1,BC= =2,则三棱柱ABC﹣
1 1 1 1
ABC 的外接球的表面积为( )
1 1 1
A.32 B.16 C.12 D.8
π π π π
【答案】D
【分析】由三棱柱ABC﹣ABC 的结构特征,把三棱柱ABC﹣ABC 放入长方体中,则长方体的外接球就
1 1 1 1 1 1是三棱柱ABC﹣ABC 的外接球,利用长方体的体对角线求出长方体的外接球的半径,从而得到
1 1 1
三棱柱ABC﹣ABC 的外接球半径,再利用球的表面积公式求出棱柱 ABC﹣ABC 的外接球的表
1 1 1 1 1 1
面积即可.
【解答】解:把三棱柱ABC﹣ABC 放入长方体中,
1 1 1
如图所示:
所以长方体的外接球即是三棱柱ABC﹣ABC 的外接球,
1 1 1
∵AB=1,BC= =2,
∴长方体的外接球的半径R= = ,
∴三棱柱ABC﹣ABC 的外接球半径为 ,
1 1 1
∴三棱柱ABC﹣ABC 的外接球的表面积为 =8 ,
1 1 1
故选:D.
π
【知识点】球的体积和表面积
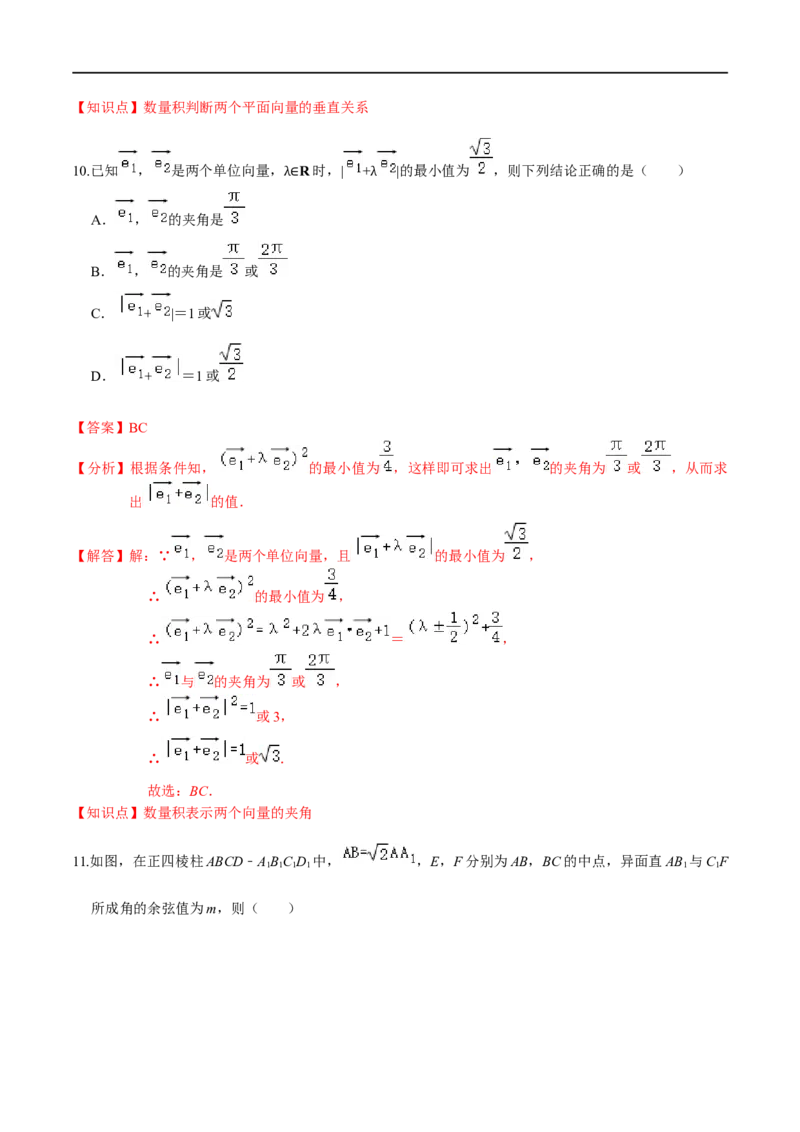
6.如图,点 M 是正方体 ABCD﹣ABC D 的棱 CD 的中点,则异面直线 AM 与 BC 所成角的余弦值是
1 1 1 1 1
( )
A. B. C. D.
【答案】A
【分析】连接AD ,证得AD∥BC ,可得∠DAM为异面直线AM与BC 所成角,连接DM,设正方体的
1 1 1 1 1 1棱长为2,求解三角形可得异面直线AM与BC 所成角的余弦值.
1
【解答】解:如图,
连接AD,∵AB=C D,AB∥C D,
1 1 1 1 1
∴四边形ABCD 为平行四边形,则AD∥BC ,
1 1 1 1
则∠DAM为异面直线AM与BC 所成角,连接DM.
1 1 1
设正方体的棱长为2,则 , .
∴cos∠ .
即异面直线AM与BC 所成角的余弦值是 .
1
故选:A.
【知识点】异面直线及其所成的角
7.如图1,已知PABC是直角梯形,AB∥PC,AB⊥BC,D在线段PC上,AD⊥PC.将△PAD沿AD折起,
使平面PAD⊥平面ABCD,连接PB,PC,设PB的中点为N,如图2.对于图2,下列选项错误的是(
)
A.平面PAB⊥平面PBC B.BC⊥平面PDC
C.PD⊥AC D.PB=2AN
【答案】A
【分析】由已知利用平面与平面垂直的性质得到 PD⊥平面ABCD,判定C正确;进一步得到平面PCD⊥
平面ABCD,结合BC⊥CD判定B正确;再证明AB⊥平面PAD,得到△PAB为直角三角形,判定
D正确;由错误的选项存在可知A错误.
【解答】解:如图,图1中AD⊥PC,则图2中PD⊥AD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PD⊥平面ABCD,则PD⊥AC,故选项C正确;
由PD⊥平面ABCD,PD 平面PDC,得平面PDC⊥平面ABCD,
而平面PDC∩平面ABCD=CD,BC 平面ABCD,BC⊥CD,
⊂
∴BC⊥平面PDC,故选项B正确;
⊂
∵AB⊥AD,平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴AB⊥平面PAD,则AB⊥PA,即△PAB是以PB为斜边的直角三角形,
而N为PB的中点,则PB=2AN,故选项D正确.
因此错误的只能是A.
故选:A.
【知识点】平面与平面垂直
8.在△OAB中,已知 ,∠AOB=45°,点P满足 ( ,µ R),其中
λ ∈
2 +µ=3满足,则| |的最小值为( )
λ
A. B. C. D.
【答案】A
【分析】根据条件可得 ,则 =( + ) + ,所以| |2=5 2﹣18 +18,即
λ μ μ λ λ
可求出最小值.
【解答】解:因为 ,∠AOB=45°,所以 ,
所以 = + ( )=( + ) + ,
λ μ λ μ μ
则| |2=( + )2+ 2=(3﹣ )2+(3﹣2 )2=5 2﹣18 +18,
λ μ μ λ λ λ λ
所以当 时,| |2取最小值 ,
则| |的最小值为 ,
故选:A.
【知识点】平面向量的基本定理二、多选题(本大题共4小题,每小题5分,选对得分,选错、少选不得分)
9.△ABC是边长为3的等边三角形,已知向量 满足 , ,则下列结论中正确的有(
)
A. 为单位向量 B.
C. D.
【答案】ABD
【分析】可画出图形,可根据条件得出 ,即得出 为单位向量;并可得出 ,从而得出 ;
根据BC边上的中线与BC垂直即可得出( ) .
【解答】解:如图,
∵ ,
∴ ,
∴ 为单位向量,
,
∴ ,
∴ ,
∵ ,
∴ .
故选:ABD.【知识点】数量积判断两个平面向量的垂直关系
10.已知 , 是两个单位向量, R时,| + |的最小值为 ,则下列结论正确的是( )
λ∈ λ
A. , 的夹角是
B. , 的夹角是 或
C. + |=1或
D. + =1或
【答案】BC
【分析】根据条件知, 的最小值为 ,这样即可求出 的夹角为 或 ,从而求
出 的值.
【解答】解:∵ , 是两个单位向量,且 的最小值为 ,
∴ 的最小值为 ,
∴ = ,
∴ 与 的夹角为 或 ,
∴ 或3,
∴ 或 .
故选:BC.
【知识点】数量积表示两个向量的夹角
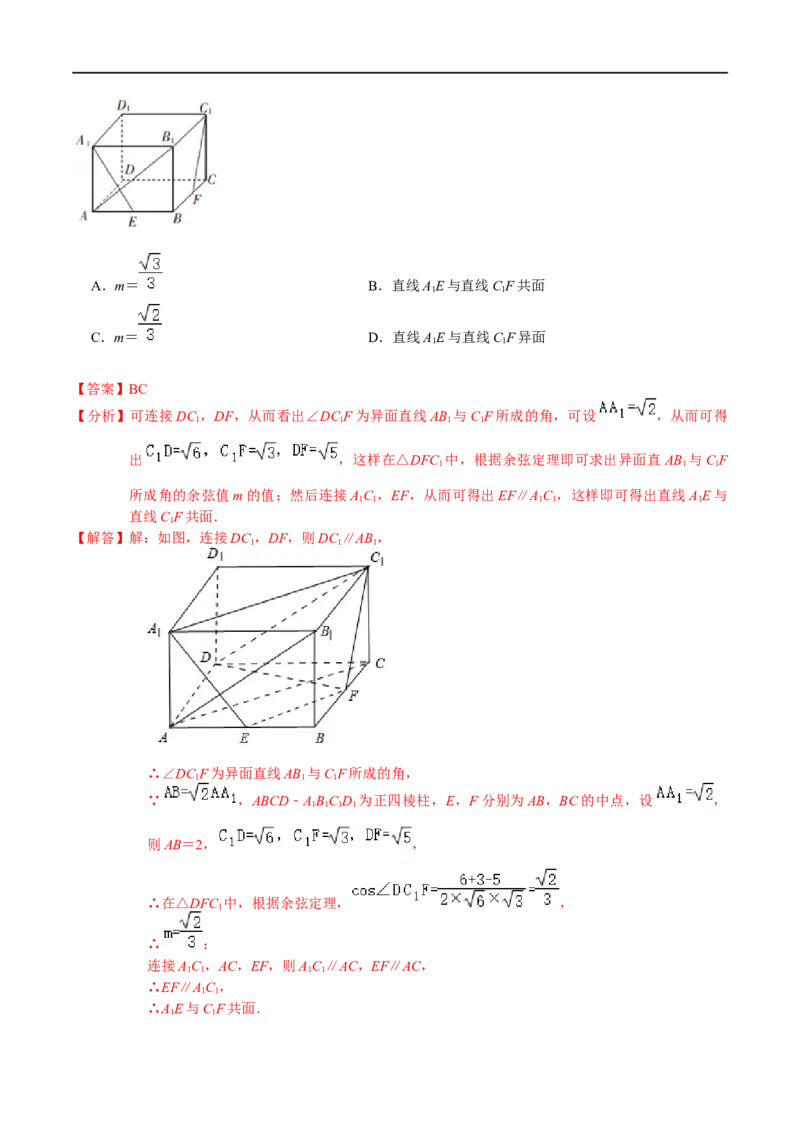
11.如图,在正四棱柱ABCD﹣ABC D 中, ,E,F分别为AB,BC的中点,异面直AB 与C F
1 1 1 1 1 1
所成角的余弦值为m,则( )A.m= B.直线AE与直线C F共面
1 1
C.m= D.直线AE与直线C F异面
1 1
【答案】BC
【分析】可连接DC ,DF,从而看出∠DC F为异面直线AB 与C F所成的角,可设 ,从而可得
1 1 1 1
出 ,这样在△DFC 中,根据余弦定理即可求出异面直 AB 与C F
1 1 1
所成角的余弦值m的值;然后连接AC ,EF,从而可得出EF∥AC ,这样即可得出直线AE与
1 1 1 1 1
直线C F共面.
1
【解答】解:如图,连接DC ,DF,则DC ∥AB,
1 1 1
∴∠DC F为异面直线AB 与C F所成的角,
1 1 1
∵ ,ABCD﹣ABC D 为正四棱柱,E,F分别为AB,BC的中点,设 ,
1 1 1 1
则AB=2, ,
∴在△DFC 中,根据余弦定理, ,
1
∴ ;
连接AC ,AC,EF,则AC ∥AC,EF∥AC,
1 1 1 1
∴EF∥AC ,
1 1
∴AE与C F共面.
1 1故选:BC.
【知识点】异面直线及其所成的角
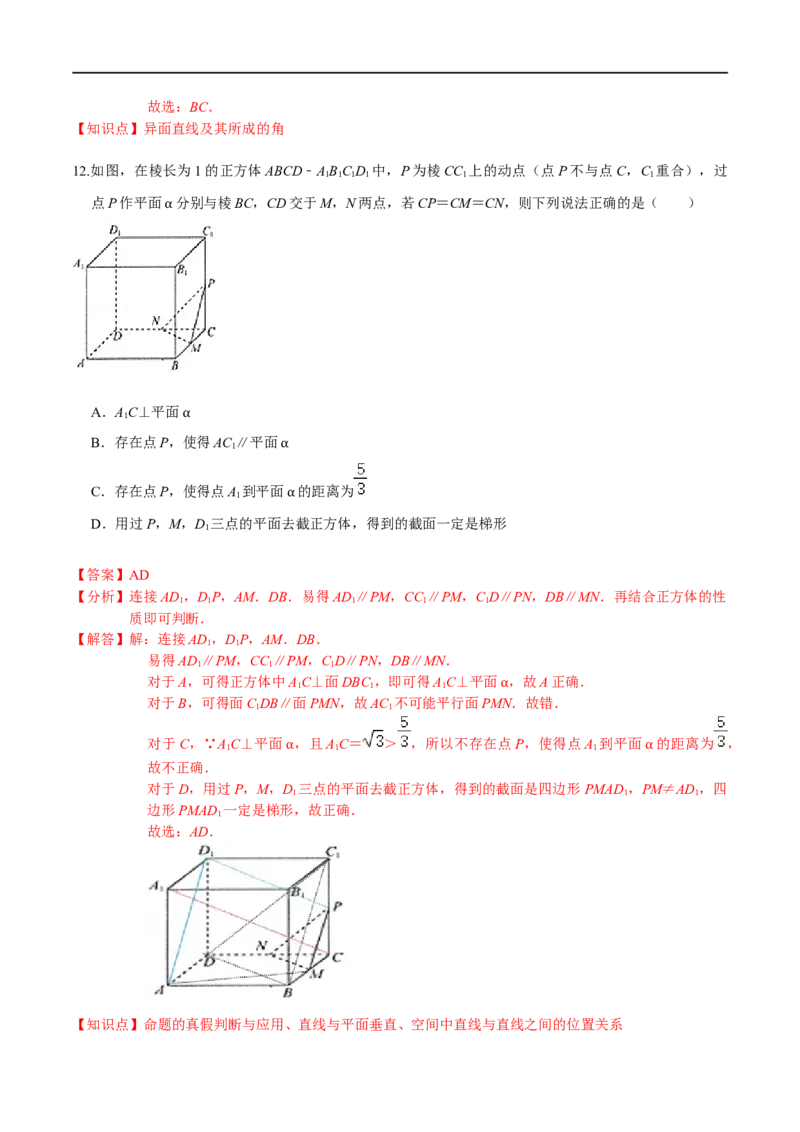
12.如图,在棱长为1的正方体ABCD﹣ABC D 中,P为棱CC 上的动点(点P不与点C,C 重合),过
1 1 1 1 1 1
点P作平面 分别与棱BC,CD交于M,N两点,若CP=CM=CN,则下列说法正确的是( )
α
A.AC⊥平面
1
B.存在点P,使α 得AC ∥平面
1
α
C.存在点P,使得点A 到平面 的距离为
1
D.用过P,M,D 三点的平面去α截正方体,得到的截面一定是梯形
1
【答案】AD
【分析】连接AD,DP,AM.DB.易得AD∥PM,CC ∥PM,C D∥PN,DB∥MN.再结合正方体的性
1 1 1 1 1
质即可判断.
【解答】解:连接AD,DP,AM.DB.
1 1
易得AD∥PM,CC ∥PM,C D∥PN,DB∥MN.
1 1 1
对于A,可得正方体中AC⊥面DBC ,即可得AC⊥平面 ,故A正确.
1 1 1
对于B,可得面C DB∥面PMN,故AC 不可能平行面PMN.故错.
1 1
α
对于C,∵AC⊥平面 ,且AC= > ,所以不存在点P,使得点A 到平面 的距离为 ,
1 1 1
故不正确.
α α
对于D,用过P,M,D 三点的平面去截正方体,得到的截面是四边形PMAD ,PM≠AD,四
1 1 1
边形PMAD 一定是梯形,故正确.
1
故选:AD.
【知识点】命题的真假判断与应用、直线与平面垂直、空间中直线与直线之间的位置关系三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.设复数z,z 满足|z|=1,|z|=2, ,则|z﹣z|= .
1 2 1 2 1 2
【分析】根据复数的几何意义得到对应向量的表示,再结合向量的平行四边形法则以及余弦定理即可求解.
【解答】解:设z,z 在复平面内对应的向量为 ,
1 2
z+z 对应的向量为 ,如图所示,
1 2
因为 ,
所以|z+z|=2,
1 2
所以 ,
又因为∠OZ Z+∠ZOZ =180 °,
1 3 1 2
所以 ,
所以 =1+4+1=6,
所以 ,故|z﹣z|= .
1 2
故答案为: .
【知识点】复数的模
14.已知向量 , 的夹角为45°,若 =(1,1),| |=2,则|2 + |= .
【分析】可得出 ,从而可求出 ,然后根据 进行数量积的运算即可
求出 的值.
【解答】解: ,∴ ,
∴ = = .
故答案为: .
【知识点】平面向量的坐标运算
15.如图,在△ABC中, =2 是BD上一点,且 = + ( R),则 的值等于 .
λ λ∈ λ
【分析】先由E在BD上,利用平面向量共线定理可设 ,然后再根据三角形法则求出向量AE,
再和所给的已知的向量AE相等即可求解.
【解答】解:因为E在BD上,所以可设 ,
则 = =
= =
=(1﹣ ) + ,
μ
又 = ,
所以 ,解得 ,
故答案为: .
【知识点】平面向量的基本定理
16.在如图直四棱柱ABCD﹣ABC D 中,底面ABCD为菱形,AA =2AB=4,∠BAD=60°,点M为棱AA
1 1 1 1 1 1
的中点,若N为菱形ABC D 内一点(不包含边界),满足MN∥平面BDC ,设直线MN与直线CC
1 1 1 1 1 1
所成角为 ,则tan 的最小值为 .
α α【分析】分别取AB 、AD 中点E、F,连结EF、ME、MF,则ME∥BC ,EF∥BD,从而平面MEF∥平
1 1 1 1 1
面BC D,由N为菱形ABC D 内一点(不包含边界),满足MN∥平面BDC ,得到点N的运动
1 1 1 1 1 1
轨迹是线段EF,(不含端点E和F),由AM∥C C,得直线MN与直线CC 所成角就是AM与
1 1 1 1
MN所成角,由MA ⊥平面ABC D ,得当N与MN中点G重合时,tan 取最小值,由此能求出
1 1 1 1 1
tan 的最小值.
α
【解答】解:分别取AB、AD 中点E、F,连结EF、ME、MF,
1 1 1 1
α
∵点M为棱AA 的中点,∴ME∥BC ,EF∥BD,
1 1
∵ME∩EF=E,BC ∩BD=B,∴平面MEF∥平面BC D,
1 1
∵N为菱形ABC D 内一点(不包含边界),满足MN∥平面BDC ,
1 1 1 1 1
∴点N的运动轨迹是线段EF,(不含端点E和F),
∵AM∥C C,∴直线MN与直线CC 所成角就是AM与MN所成角,
1 1 1 1
∵MA ⊥平面ABC D,∴当N与MN中点G重合时,tan 取最小值,
1 1 1 1 1
α
此时,AM= =2,AG= = = ,
1 1
∴tan 的最小值为:
α
tan = = = .
α
∴tan 的最小值为 .
α
故答案为: .【知识点】异面直线及其所成的角
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.已知复数z= +(a2﹣1)i,z=2+2(a+1)i(a R,i是虚数单位).
1 2
(1)若复数z﹣z 在复平面上对应点落在第一象限,求∈实数a的取值范围;
1 2
(Ⅱ)若虚数z 是实系数一元二次方程4x2﹣4x+m=0的根,求实数m值.
1
【分析】(1)由复数对应的点在第一象限得到实部大于0,虚部大于0,解不等式组即可;
(Ⅱ)利用z 是实系数一元二次方程4x2﹣4x+m=0的根,得到另一个根是复数z 的共轭复数,
1 1
利用根与系数的关系得到a和m.
【解答】解:(Ⅰ由已知得到z﹣z = ﹣2+(a2﹣2a﹣3)i,因为在复平面上对应点落在第一象限,所
1 2
以 ,解得 ,所以 ;
(Ⅱ)因为虚数z 是实系数一元二次方程4x2﹣4x+m=0的根,所以 是方程的另一个根,所
1 1
以 =1,所以a=0,
所以 , ,
所以 ,所以m=5.【知识点】复数的运算
18.已知复数z=m(m﹣1)+(m2﹣1)i,其中m R,i是虚数单位.
(Ⅰ)当m为何值时,复数z是纯虚数? ∈
(Ⅱ)若复数z对应的点在复平面内第二、四象限角平分线上,求z的模|z|.
【分析】(Ⅰ)直接由实部为0且虚部不为0列式求解;
(Ⅱ)由实部与虚部的和等于0列式求得m,进一步求得z,则|z|可求.
【解答】解:(Ⅰ)由 ,解得m=0;
(Ⅱ)∵复数z对应的点在复平面内第二、四象限角平分线上,
∴m(m﹣1)+m2﹣1=0,即2m2﹣m﹣1=0,解得m= 或m=1.
当m=﹣ 时,z= ,则|z|= = ;
当m=1时,z=0,则|z|=0.
【知识点】复数的代数表示法及其几何意义
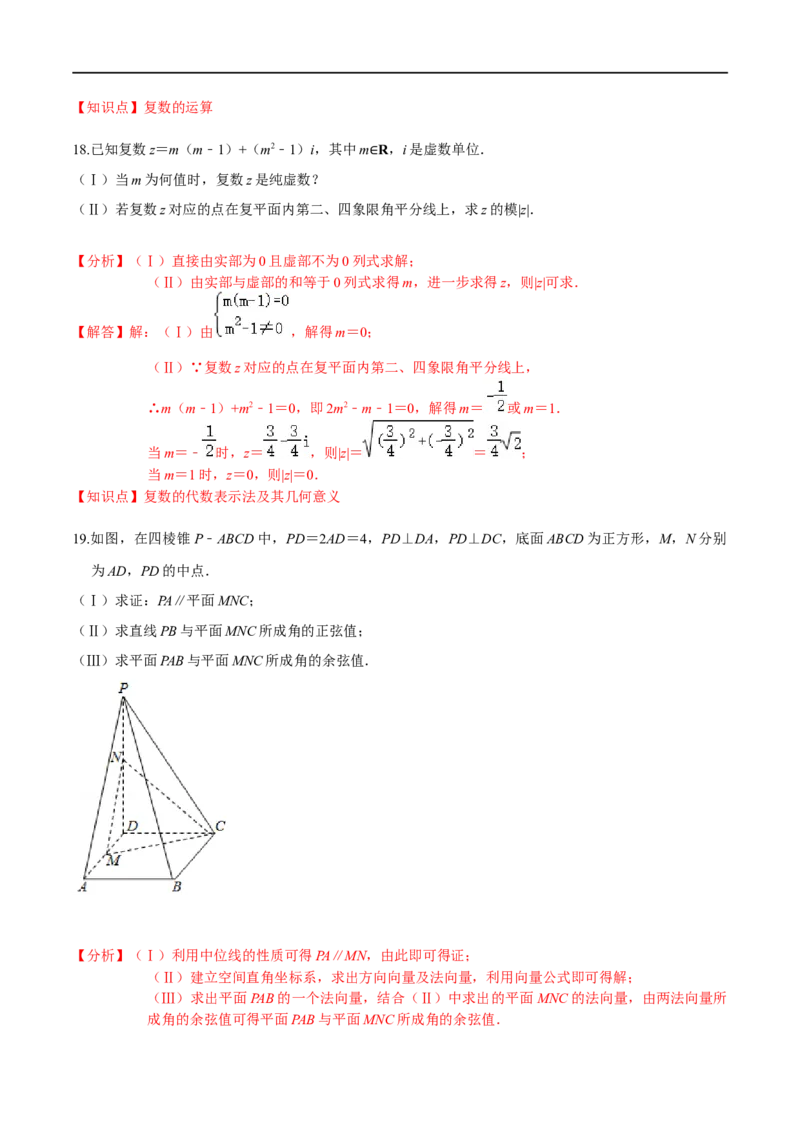
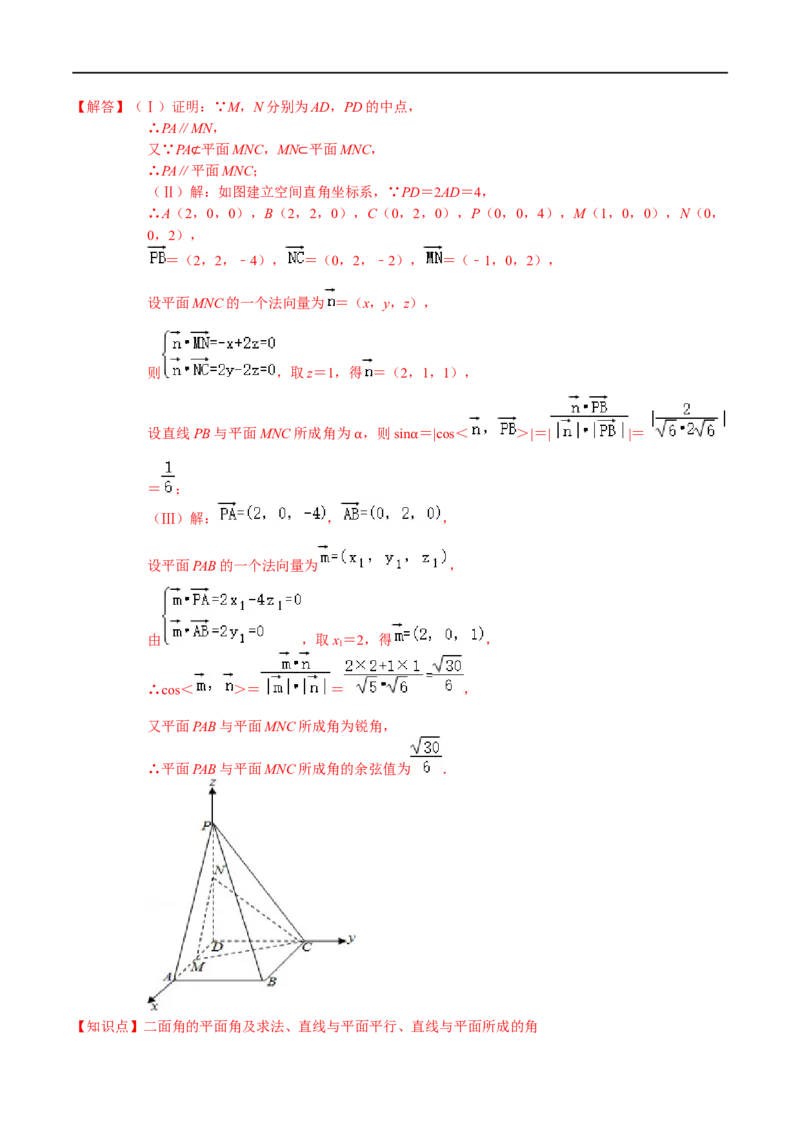
19.如图,在四棱锥P﹣ABCD中,PD=2AD=4,PD⊥DA,PD⊥DC,底面ABCD为正方形,M,N分别
为AD,PD的中点.
(Ⅰ)求证:PA∥平面MNC;
(Ⅱ)求直线PB与平面MNC所成角的正弦值;
(Ⅲ)求平面PAB与平面MNC所成角的余弦值.
【分析】(Ⅰ)利用中位线的性质可得PA∥MN,由此即可得证;
(Ⅱ)建立空间直角坐标系,求出方向向量及法向量,利用向量公式即可得解;
(Ⅲ)求出平面PAB的一个法向量,结合(Ⅱ)中求出的平面MNC的法向量,由两法向量所
成角的余弦值可得平面PAB与平面MNC所成角的余弦值.【解答】(Ⅰ)证明:∵M,N分别为AD,PD的中点,
∴PA∥MN,
又∵PA 平面MNC,MN 平面MNC,
∴PA∥平面MNC;
⊄ ⊂
(Ⅱ)解:如图建立空间直角坐标系,∵PD=2AD=4,
∴A(2,0,0),B(2,2,0),C(0,2,0),P(0,0,4),M(1,0,0),N(0,
0,2),
=(2,2,﹣4), =(0,2,﹣2), =(﹣1,0,2),
设平面MNC的一个法向量为 =(x,y,z),
则 ,取z=1,得 =(2,1,1),
设直线PB与平面MNC所成角为 ,则sin =|cos< >|=| |=
α α
= ;
(Ⅲ)解: , ,
设平面PAB的一个法向量为 ,
由 ,取x=2,得 ,
1
∴cos< >= = ,
又平面PAB与平面MNC所成角为锐角,
∴平面PAB与平面MNC所成角的余弦值为 .
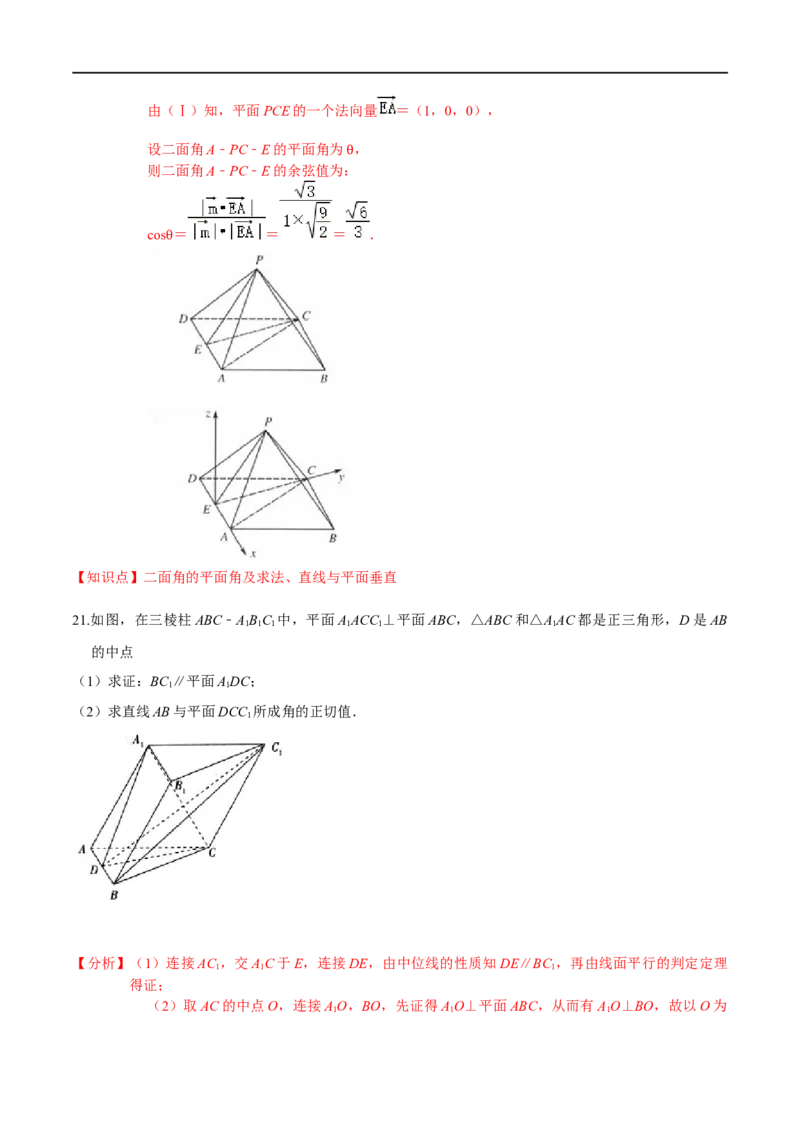
【知识点】二面角的平面角及求法、直线与平面平行、直线与平面所成的角20.如图所示,四棱锥P﹣ABCD中,四边形ABCD为平行四边形,AD=DC=AC,且CP⊥平面PAD,E为
AD的中点
(Ⅰ)证明:AD⊥平面PCE;
(Ⅱ)若PA= AD,求二面角A﹣PC﹣E的余弦值.
【分析】(Ⅰ)连接AC,推导出AD⊥CE,AD⊥CP,由此能证明AD⊥平面PCE.
(Ⅱ)以点F为坐标原点,EA为x轴,EC为y轴,过点E作垂直于平面ABCD的直线为z轴,
建立空间直角坐标系,利用向量法能求出二面角A﹣PC﹣E的余弦值.
【解答】解:(Ⅰ)证明:如图,连接AC,∵AD=DC=AC,∴△ADC为等边三角形,
∵点E为AD的中点,∴AD⊥CE,
∵CP⊥平面PAD,AD 平面PAD,∴AD⊥CP,
∵CP∩CE=C,∴AD⊥平面PCE.
⊂
(Ⅱ)如图,以点F为坐标原点,EA为x轴,EC为y轴,
过点E作垂直于平面ABCD的直线为z轴,建立空间直角坐标系,
则E(0,0,0),设点A(1,0,0),则C(0, ,0),
由(Ⅰ)知AD⊥平面PCE,
设P(0,y,z),(y>0,z>0),
∵PA= AD,∴PA= ,PC=1,
∴ ,解得y= ,z= ,∴P(0, , ),
∴ =(0, ,﹣ ), =(﹣1, ,0),
设平面PAC的法向量 =(x,y,z),
则 ,取y=1,得 =( ),由(Ⅰ)知,平面PCE的一个法向量 =(1,0,0),
设二面角A﹣PC﹣E的平面角为 ,
则二面角A﹣PC﹣E的余弦值为:
θ
cos = = = .
θ
【知识点】二面角的平面角及求法、直线与平面垂直
21.如图,在三棱柱ABC﹣ABC 中,平面AACC ⊥平面ABC,△ABC和△AAC都是正三角形,D是AB
1 1 1 1 1 1
的中点
(1)求证:BC ∥平面ADC;
1 1
(2)求直线AB与平面DCC 所成角的正切值.
1
【分析】(1)连接AC ,交AC于E,连接DE,由中位线的性质知DE∥BC ,再由线面平行的判定定理
1 1 1
得证;
(2)取AC的中点O,连接AO,BO,先证得AO⊥平面ABC,从而有AO⊥BO,故以O为
1 1 1原点,OB、OC、OA 所在直线分别为 x、y、z轴建立空间直角坐标系,设直线 AB与平面
1
DCC 所成的角为 ,求得平面DCC 的法向量 后,由sin =|cos< , >|,即可得解.
1 1
θ θ
【解答】(1)证明:连接AC ,交AC于E,连接DE,
1 1
∵四边形AACC 是平行四边形,
1 1
∴E是AC 的中点,
1
∵D是AB的中点,∴DE∥BC ,
1
∵DE 平面ADC,BC 平面ADC,
1 1 1
∴BC ∥平面ADC.
1 1
⊂ ⊄
(2)解:取AC的中点O,连接AO,BO,
1
∵△ABC和△AAC都是正三角形,∴AO⊥AC,BO⊥AC,
1 1
∵平面AACC ⊥平面ABC,平面AACC ∩平面ABC=AC,
1 1 1 1
∴AO⊥平面ABC,∴AO⊥BO,
1 1
以O为原点,OB、OC、OA 所在直线分别为x、y、z轴建立如图所示的空间直角坐标系,
1
设AC=2,则A(0,﹣1,0),B( ,0,0),C(0,1,0),D( , ,0),C
1
(0,2, ),
∴ =( ,1,0), =( , ,0), =( , , ),
设平面DCC 的法向量为 =(x,y,z),则 ,即 ,
1
令x=3,则y= ,z=﹣1,∴ =(3, ,﹣1),
设直线 AB 与平面 DCC 所成的角为 ,则 sin =|cos< , >|=| |=|
1
θ θ
|= ,
∴tan = ,
故直线AB与平面DCC 所成角的正切值为 .
1
θ
【知识点】直线与平面平行、直线与平面所成的角
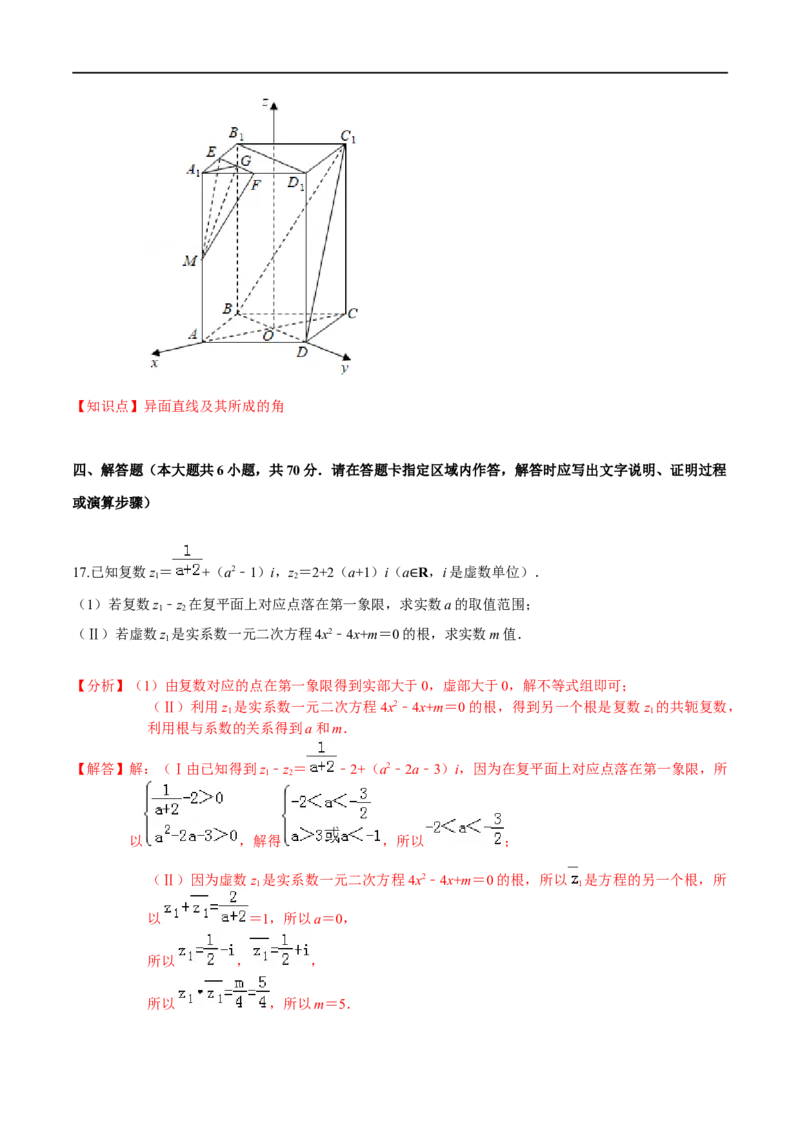
22.如图,在四棱柱C﹣ABEF中,平面ABEF⊥平面ABC,△ABC是边长为2的等边三角形,AB∥EF,∠ABE=90°,BE=EF=1,点M为BC的中点
(Ⅰ)求证:EM∥平面ACF;
(Ⅱ)求二面角E﹣BC﹣F的余弦值;
(Ⅲ)在线段EF上是否存在一点N,使直线CN与平面BCF所成的角正弦值为 ,若存在求出EN的长,
若不存在说明理由.
【分析】(Ⅰ)取AC中点P,连结MP、FP,推导出四边形EFPM是平行四边形,从而FP∥EM,由此能
证明EM∥平面ACF.
(Ⅱ)取AB中点O,连结CO,FO,推导出FO⊥平面ABC,OC⊥AB,以O为原点,OC为x
轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣BC﹣F的余
弦值.
(Ⅲ)假设在线段EF上是存在一点N,使直线CN与平面BCF所成的角正弦值为 ,设
EN=t.利用向量法能求出结果.
【解答】解:(Ⅰ)证明:取AC中点P,连结MP、FP,
∵△ABC是边长为2的等边三角形,AB∥EF,∠ABE=90°,BE=EF=1,点M为BC的中点,
∴EF MP,∴四边形EFPM是平行四边形,∴FP∥EM,
∵EM 平面ACF,FP 平面ACF,
∴EM∥平面ACF.
⊄ ⊂
(Ⅱ)解:取AB中点O,连结CO,FO,
∵在四棱柱C﹣ABEF中,平面ABEF⊥平面ABC,△ABC是边长为2的等边三角形,
AB∥EF,∠ABE=90°,BE=EF=1,点M为BC的中点,
∴FO⊥平面ABC,OC⊥AB,
以O为原点,OC为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,
B(0,1,0),C( ,0,0),E(0,1,1),F(0,0,1),
=( ,﹣1,0), =(0,0,1), =(0,﹣1,1),
设平面BCE的法向量 =(x,y,z),则 ,取x=1,得 =(1, ,0),
设平面BCF的法向量 =(a,b,c),
则 ,取a=1,得 =(1, ),
设二面角E﹣BC﹣F的平面角为 ,
θ
则cos = = = .
θ
∴二面角E﹣BC﹣F的余弦值为 .
(Ⅲ)解:假设在线段EF上是存在一点N,使直线CN与平面BCF所成的角正弦值为 ,
设EN=t.
则N(0,1﹣t,1), =(﹣ ,1﹣t,1),平面BCF的法向量 =(1, ),
∴|cos< >|= = = ,
解得t=1﹣ ,
∴线段EF上是存在一点N,EN=1﹣ ,使直线CN与平面BCF所成的角正弦值为 .
【知识点】直线与平面所成的角、直线与平面平行、二面角的平面角及求法