文档内容
期中检测卷 05
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.设S 为等差数列{a}的前n项和,且a﹣a+a=6,则S =( )
n n 3 5 8 11
A.55 B.66 C.110 D.132
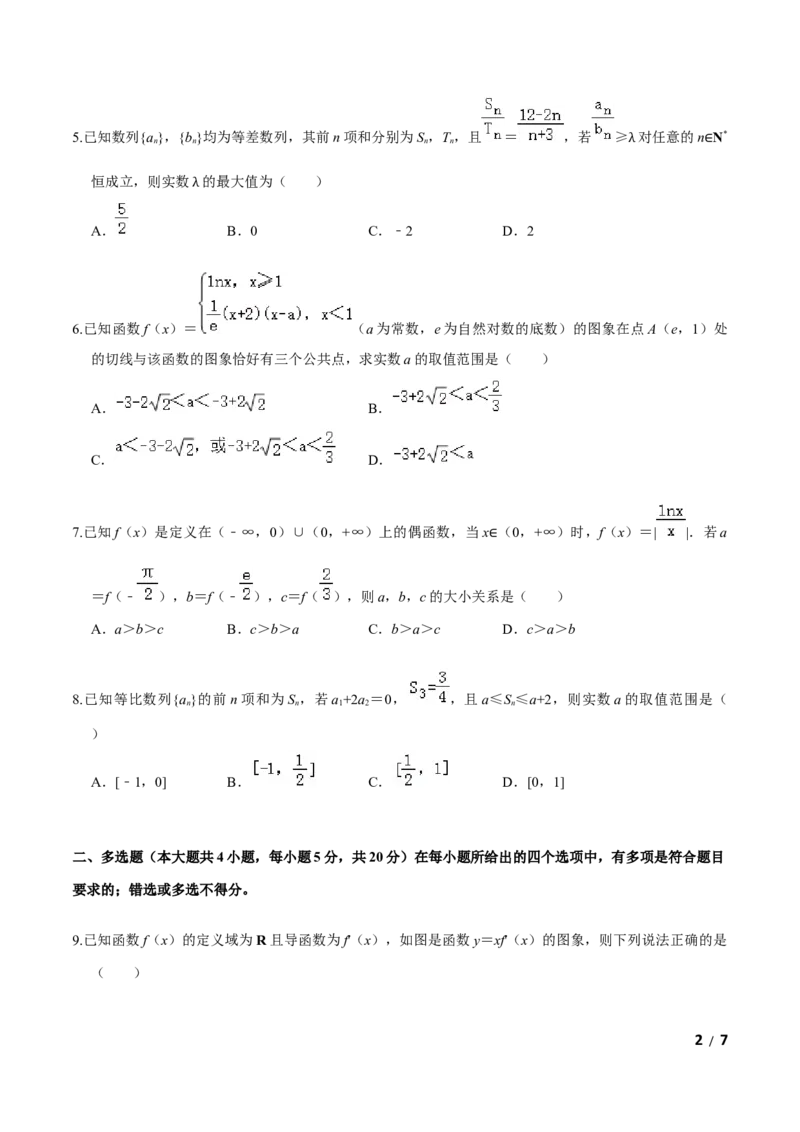
2.已知曲线 在x=0处的切线l过点(﹣3,﹣a),则实数a等于( )
A.2 B.﹣2 C.3 D.﹣3
3.《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到
了很大的作用,是东方古代数学的名著,在这部著作中,许多数学问题都是以歌诀形式呈现的.“九儿
问甲歌”就是其中一首:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百一十六,借问
大儿多少岁,各儿岁数要谁推.这位公公年龄最大的儿子年龄为( )
A.9岁 B.12岁 C.21岁 D.36岁
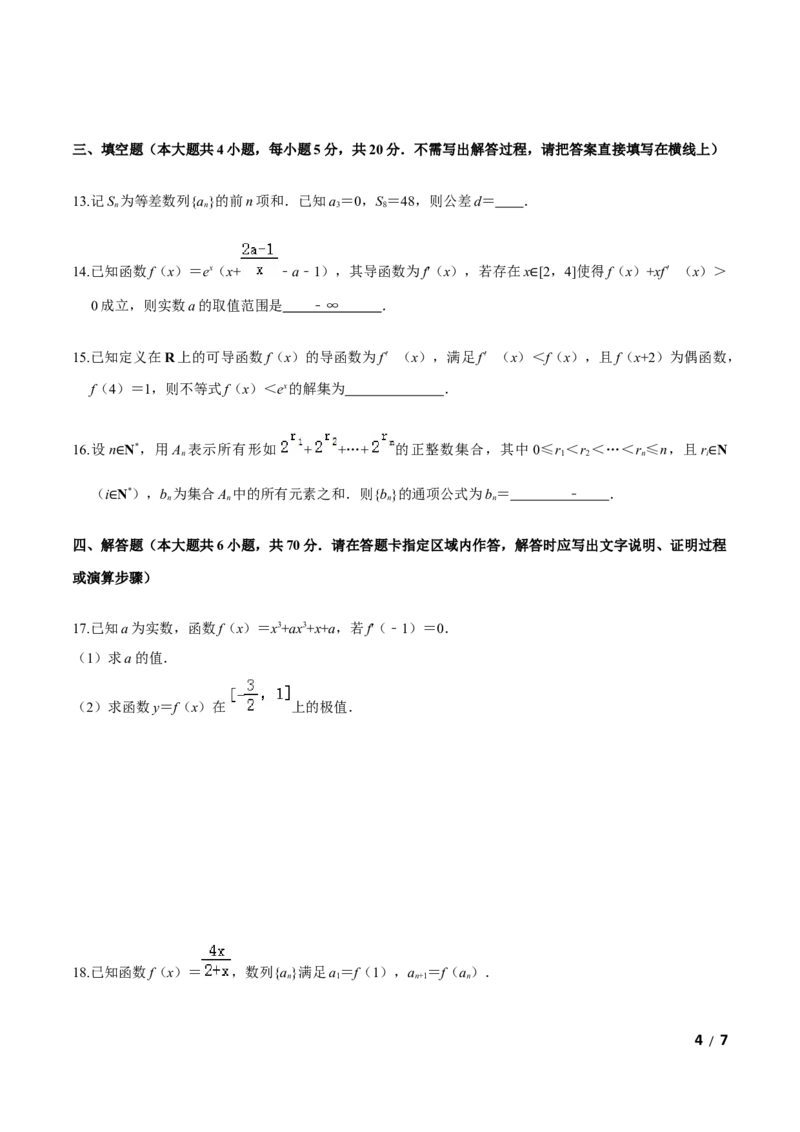
4.已知函数y=f(x)(x R)的图象如图所示,则不等式 <0的解集为( )
∈
A.(﹣∞,0)∪( ,2) B.(﹣1,1)∪(1,3)
C.(﹣∞, )∪( ,2) D.(﹣∞, )(1,2)
1 / 75.已知数列{a},{b}均为等差数列,其前n项和分别为S,T,且 = ,若 ≥ 对任意的n N*
n n n n
λ ∈
恒成立,则实数 的最大值为( )
λ
A. B.0 C.﹣2 D.2
6.已知函数f(x)= (a为常数,e为自然对数的底数)的图象在点A(e,1)处
的切线与该函数的图象恰好有三个公共点,求实数a的取值范围是( )
A. B.
C. D.
7.已知f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x (0,+∞)时,f(x)=| |.若a
∈
=f(﹣ ),b=f(﹣ ),c=f( ),则a,b,c的大小关系是( )
A.a>b>c B.c>b>a C.b>a>c D.c>a>b
8.已知等比数列{a}的前n项和为S ,若a+2a =0, ,且a≤S≤a+2,则实数a的取值范围是(
n n 1 2 n
)
A.[﹣1,0] B. C. D.[0,1]
二、多选题(本大题共4小题,每小题5分,共20分)在每小题所给出的四个选项中,有多项是符合题目
要求的;错选或多选不得分。
9.已知函数f(x)的定义域为R且导函数为f'(x),如图是函数y=xf'(x)的图象,则下列说法正确的是
( )
2 / 7A.函数f(x)的增区间是(﹣2,0),(2,+∞)
B.函数f(x)的增区间是(﹣∞,﹣2),(2,+∞)
C.x=﹣2是函数的极小值点
D.x=2是函数的极小值点
10.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此
六日过其关.则下列说法正确的是( )
A.此人第二天走了九十六里路
B.此人第一天走的路程比后五天走的路程多六里
C.此人第三天走的路程占全程的
D.此人后三天共走了42里路
11.等比数列{a}中,公比为q,其前n项积为T,并且满足a>1.a •a ﹣1>0, <0,下列选项
n n 1 99 100
中,正确的结论有( )
A.0<q<1
B.a •a ﹣1<0
99 101
C.T 的值是T 中最大的
100 n
D.使T>1成立的最大自然数n等于198
n
12.已知函数f(x)=ex﹣alnx的定义域是D,有下列四个命题,其中正确的有( )
A.对于∀a (﹣∞,0),函数f(x)在D上是单调增函数
B.对于∀a∈(0,+∞),函数f(x)存在最小值
C.存在a (∈ ﹣∞,0),使得对于任意x D,都有f(x)>0成立
D.存在a∈(0,+∞),使得函数f(x)有∈两个零点
3 / 7
∈三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.记S 为等差数列{a}的前n项和.已知a=0,S=48,则公差d= .
n n 3 8
14.已知函数f(x)=ex(x+ ﹣a﹣1),其导函数为f'(x),若存在x [2,4]使得f(x)+xf′(x)>
0成立,则实数a的取值范围是 ﹣∞ . ∈
15.已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,
f(4)=1,则不等式f(x)<ex的解集为 .
16.设n N*,用A 表示所有形如 + +…+ 的正整数集合,其中0≤r <r <…<r≤n,且r N
n 1 2 n i
∈ ∈
(i N*),b 为集合A 中的所有元素之和.则{b}的通项公式为b= ﹣ .
n n n n
∈
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.已知a为实数,函数f(x)=x3+ax3+x+a,若f'(﹣1)=0.
(1)求a的值.
(2)求函数y=f(x)在 上的极值.
18.已知函数f(x)= ,数列{a}满足a=f(1),a =f(a).
n 1 n+1 n
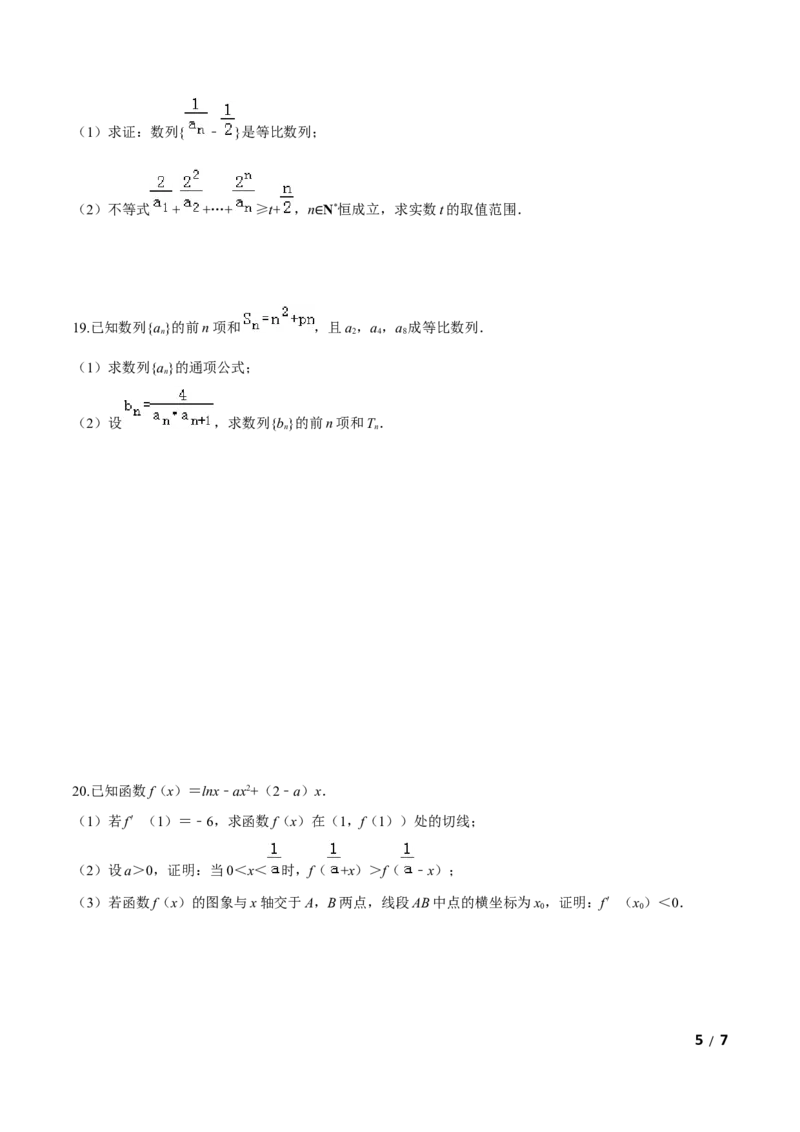
4 / 7(1)求证:数列{ ﹣ }是等比数列;
(2)不等式 + +…+ ≥t+ ,n N*恒成立,求实数t的取值范围.
∈
19.已知数列{a}的前n项和 ,且a,a,a 成等比数列.
n 2 4 8
(1)求数列{a}的通项公式;
n
(2)设 ,求数列{b}的前n项和T.
n n
20.已知函数f(x)=lnx﹣ax2+(2﹣a)x.
(1)若f′(1)=﹣6,求函数f(x)在(1,f(1))处的切线;
(2)设a>0,证明:当0<x< 时,f( +x)>f( ﹣x);
(3)若函数f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x,证明:f′(x)<0.
0 0
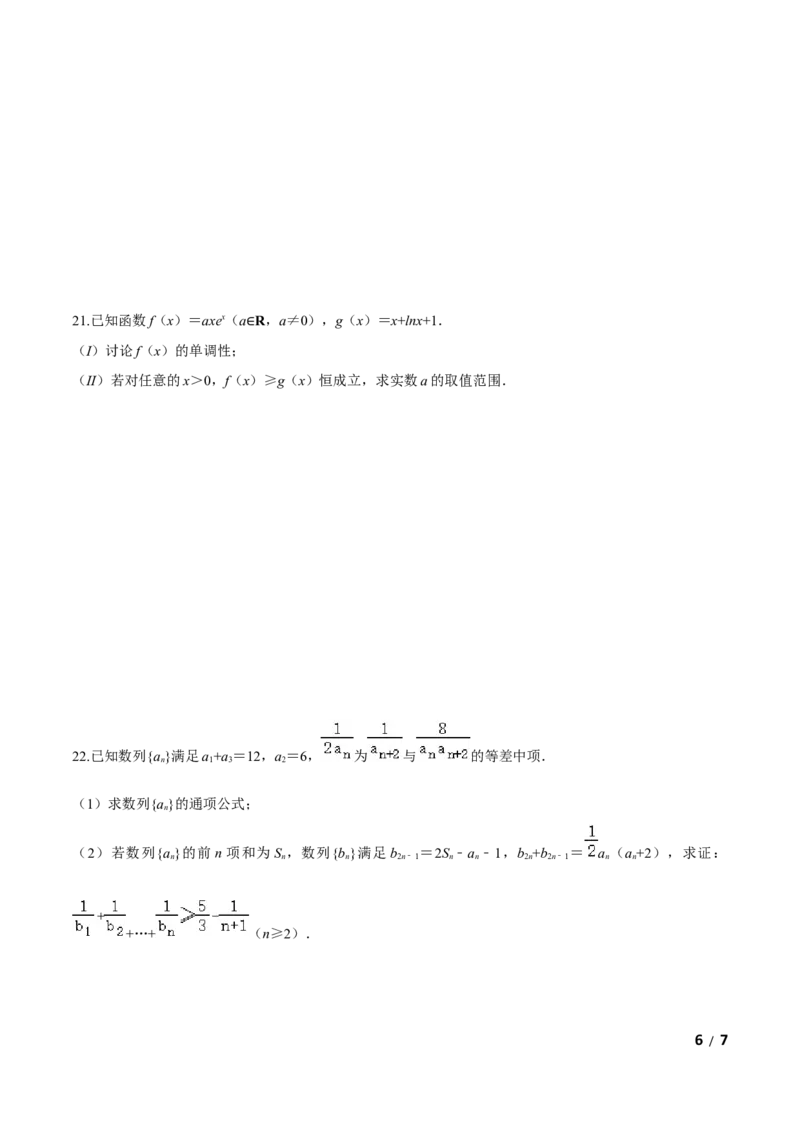
5 / 721.已知函数f(x)=axex(a R,a≠0),g(x)=x+lnx+1.
(I)讨论f(x)的单调性;∈
(II)若对任意的x>0,f(x)≥g(x)恒成立,求实数a的取值范围.
22.已知数列{a}满足a+a=12,a=6, 为 与 的等差中项.
n 1 3 2
(1)求数列{a}的通项公式;
n
(2)若数列{a}的前n项和为S ,数列{b}满足b =2S﹣a﹣1,b +b = a (a+2),求证:
n n n 2n﹣1 n n 2n 2n﹣1 n n
+…+ (n≥2).
6 / 77 / 7