文档内容
2024-2025 学年天津市静海区第一中学高一下学期 3 月学生学业能力调
研数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知A(1,0)、B(2,1),若向量 是与
A
⇀
B
方向相同的单位向量,则 ⃗ a=( )
A. B. C. (√2 √2) D. (√2 √2)
(1,1) (1,0) ,− ,
2 2 2 2
⃗ ⃗ ⃗ ⃗ 3√3
2.已知⃗a,⃗b均为单位向量,(2a+b)⋅(a−2b)=− ,则⃗a与⃗b的夹角为( )
2
π π π π
A. B. C. D.
6 3 4 2
3.在▵ABC中,若a=5√2,c=10,A=30 ∘,则B等于( )
A. 105° B. 60°或120° C. 15° D. 105°或15°
4.设 ⃗a ,⃗b 是非零向量,“⃗
a⋅
⃗
b=
|⃗
a
||⃗
b
|”是“ ⃗a//⃗b ”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
1
5.在▵ABC中,内角A、B、C所对的边分别为a、b、c,a=√3,A=60∘,若cos2B= ,则b=( )
2
A. 1 B. √3 C. 2 D. 2√2
第 页,共 页
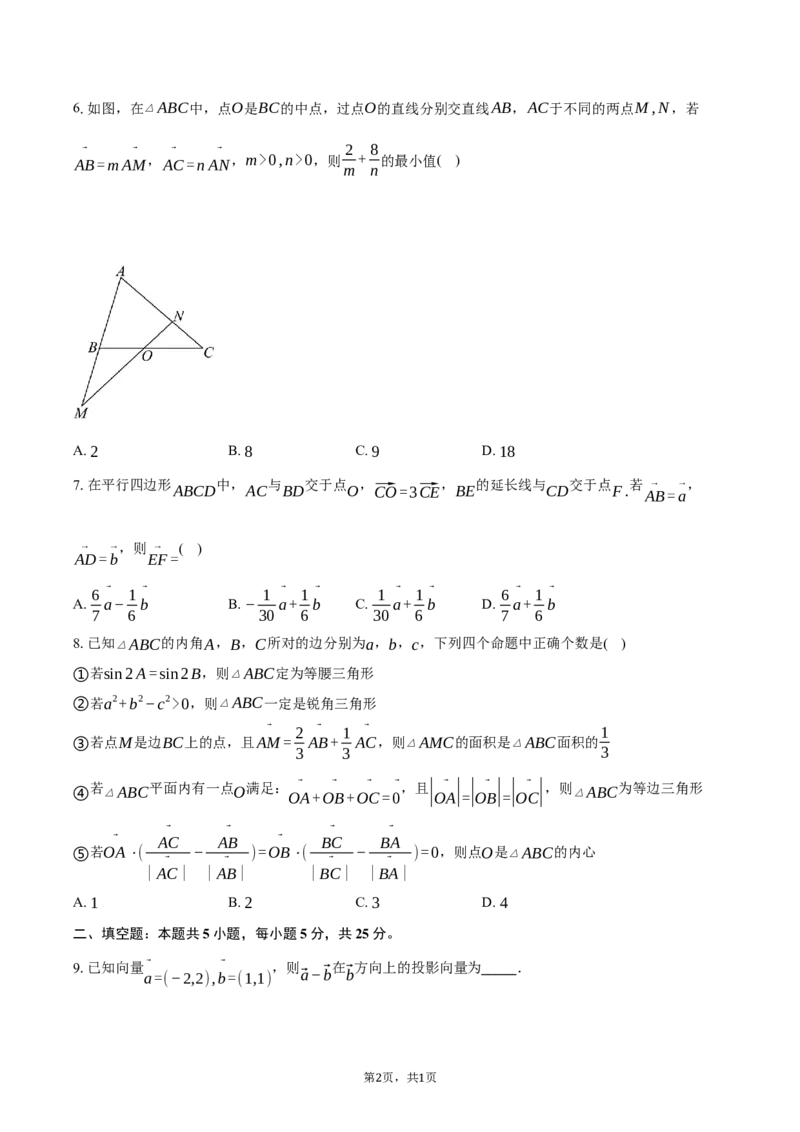
1 16.如图,在▵ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若
2 8
A ⃗ B=mA ⃗ M , A ⃗ C=nA ⃗ N ,m>0,n>0,则 + 的最小值( )
m n
A. 2 B. 8 C. 9 D. 18
7.在平行四边形 中, 与 交于点 , , 的延长线与 交于点 若 → →,
ABCD AC BD O ⃗CO=3⃗CE BE CD F.
AB=a
→ →,则 → ( )
AD=b EF=
6⃗ 1⃗ 1 ⃗ 1⃗ 1 ⃗ 1⃗ 6⃗ 1⃗
A. a− b B. − a+ b C. a+ b D. a+ b
7 6 30 6 30 6 7 6
8.已知▵ABC的内角A,B,C所对的边分别为a,b,c,下列四个命题中正确个数是( )
①若sin2A=sin2B,则▵ABC定为等腰三角形
②若a2+b2−c2>0,则▵ABC一定是锐角三角形
⃗ 2 ⃗ 1 ⃗ 1
③若点M是边BC上的点,且AM= AB+ AC,则▵AMC的面积是▵ABC面积的
3 3 3
若 平面内有一点 满足: ⃗ ⃗ ⃗ ⃗,且| ⃗ | | ⃗ | | ⃗ |,则 为等边三角形
④ ▵ABC O OA+OB+OC=0 OA = OB = OC ▵ABC
⃗ ⃗ ⃗ ⃗
⃗ AC AB ⃗ BC BA
⑤若OA⋅( − )=OB⋅( − )=0,则点O是▵ABC的内心
⃗ ⃗ ⃗ ⃗
|AC| |AB| |BC| |BA|
A. 1 B. 2 C. 3 D. 4
二、填空题:本题共5小题,每小题5分,共25分。
9.已知向量⃗
a=(−2,2),
⃗
b=(1,1)
,则
⃗a−⃗b
在
⃗b
方向上的投影向量为 .
第 页,共 页
2 1π
10.在ΔABC中,若ac=8,a+c=7,B= ,则b= .
3
11.已知向量⃗
a=(1,2)
,⃗
b=(x,1).
若⟨⃗
a,
⃗
b
⟩为锐角,则
x
的取值范围是 .
12.如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得
AD⊥CD,AD=10km,AB=14km,∠BAD=60∘,∠BCD=135∘,则两景点B与C的距离为 km.
13.在平面四边形ABCD中, | A ⃗ B | = | B ⃗ C | = | C ⃗ D | =D ⃗ A⋅D ⃗ C=1,B ⃗ A⋅B ⃗ C= 1 ,则 | A ⃗ C | = ;
2
⃗ ⃗ .
BD⋅CD=
三、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
14.(本小题13分)
已知平面向量⃗ ⃗ ⃗,⃗ ⃗ ⃗,其中⃗ ,⃗ .
a=−3e +2e b=5e +e e =(1,0) e =(0,1)
1 2 1 2 1 2
(1)求 与 的夹角θ;
(2) 若⃗ c=4e ⃗ −2e ⃗与 k ⃗ a+ ⃗ b 共线,求实数 k 的值.
1 2
15.(本小题15分)
在 中,内角 所对的边分别为 已知 , .
▵ABC A,B,C a,b,c. asin A=4bsinB ac=√5(a2−b2−c2 )
(I)求cosA的值;
(II)求sin(2B−A)的值.
16.(本小题15分)
在三角形ABC中,已知内角A,B,C所对的边分别为a,b,c,a=3√2,b=3,cosA=cos2B.
(1)求边c的长;
第 页,共 页
3 1(2) 若 D 为直线 BC 上的一点,且|
C
⇀
D
|
=2
|
B
⇀
D
|,求|
A
⇀
D
|.
17.(本小题17分)
⃗ 2 ⃗
如图,在边长为1的正方形ABCD中,P是对角线AC上一点,且AP= AC,则
5
求 ⃗ ⃗ ;
(1)
DP⋅BP
若点 为线段 含端点 上的动点,求 ⃗ ⃗ 的最小值;
(2) M BD( )
MP⋅MB
(3)求数量积是向量中常见常考的问题,根据本题试总结常用的求数量积的方法以及每个方法适用范围.
18.(本小题17分)
在▵ABC中,角A,B,C所对的边分别为a,b,c,已知asinB=bsin2A.
(1)求角A的大小.
(2)若b=3,▵ABC的面积为3√3,求▵ABC的周长.
(3)若▵ABC为锐角三角形,求2cosB+cosC的取值范围.
第 页,共 页
4 1参考答案
1.D
2.A
3.D
4.A
5.A
6.C
7.B
8.B
9. ̂(cid:29)
−b/(−1,−1)
10.5
1 1
11.(−2, )∪( ,+∞)
2 2
12.3√2
√3
13.1 ;1+
2
14. 因为⃗ ,⃗ ,
(1) e =(1,0) e =(0,1)
1 2
所以⃗ ⃗ ⃗ ,⃗ ⃗ ⃗ ,
a=−3e +2e =(−3,2) b=5e +e =(5,1)
1 2 1 2
⃗ ⃗ , ⃗ ⃗ ,
a⋅b=−3×5+2=−13 |a|=√13,|b|=√26
→ →
a⋅b −13 √2
∴cosθ= = =− ,
→ → √13×√26 2
|a||b|
3π
∵0≤θ≤π,∴θ= .
4
⃗ ⃗ ⃗ , ⃗ ⃗ ,
(2)c=4e −2e =(4,0)−(0,2)=(4,−2) ka+b=k(−3,2)+(5,1)=(5−3k,2k+1)
1 2
∵
⃗
c=4e
⃗
−2e
⃗与
k
⃗
a+
⃗
b
共线, ∴4(2k+1)+2(5−3k)=0,
1 2
解得k=−7.
即实数k的值为−7.
第 页,共 页
5 1a b
15.(Ⅰ)解:由asinA=4bsinB,及 = ,得a=2b.
sin A sinB
√5
− ac
由ac=√5(a2−b2−c2),及余弦定理,得 b2+c2−a2 5 √5.
cosA= = =−
2bc ac 5
2√5 asin A √5
(Ⅱ)解:由(Ⅰ),可得sin A= ,代入asinA=4bsinB,得sinB= = .
5 4b 5
2√5 4
由(Ⅰ)知,A为钝角,所以cosB=√1−sin2B= .于是sin2B=2sinBcosB= ,
5 5
3
cos2B=1−2sin2B= ,故
5
4 ( √5) 3 2√5 2√5.
sin(2B−A)=sin2BcosA−cos2Bsin A= × − − × =−
5 5 5 5 5
16.(1)方法一:∵a=3√2,b=3,∴sin A=√2sinB①.
又cosA=cos2B ②,所以①与②平方相加得2sin2B+cos22B=1,
即cos22B−cos2B=0,∴cos2B=0或cos2B=1.
又a>b,∴B为锐角,∴0<2B<π,∴cos2B=0,B=45 ∘.
∴sin A=√2sinB=1,∴A=90 ∘,所以ΔABC为等腰直角三角形,∴c=b=3.
方法二:∵a>b,∴B为锐角,∴0<2B<π,∵cosA=cos2B,∴A=2B.
∴sinA=sin2B=2sinBcosB,
也可以直接由 得 ,即
( cosA=cos2B 1−cos2A=1−cos22B sin2A=sin22B).
a2+c2−b2
由正弦定理与余弦定理得:a=2b ,
2ac
又∵a=3√2,b=3,∴c2−6c+9=0,即c=3.
(2) 解法一: (i) 当
C
⇀
D=−2B
⇀
D
时,
⇀ ⇀ ⇀ ⇀ 2 ⇀ ⇀ 2 ⇀ 2 ⇀ 2 ⇀ 1 ⇀
AD=AC+CD=AC+ CB =AC+ AB− AC= AB+ AC,
3 3 3 3 3
| ⇀ | √4 ⇀ 2 ⇀ 1 ⇀ 1 ⇀ ;
∴AD = AB2+2⋅ AB⋅ AC+ AC2=√5
9 3 3 9
(ii) 当
C
⇀
D=2B
⇀
D
时,
第 页,共 页
6 1⇀ ⇀ ⇀ ⇀ ⇀ ⇀ ⇀ ⇀ ⇀ ⇀ ,
AD=AC+CD=AC+2CB =AC+2AB−2AC=2AB−AC
| ⇀ | √ ⇀ ⇀ ⇀ ⇀ .
∴AD = 4AB2−2⋅2AB⋅AC+AC2=3√5
解法二: (i) 当
C
⇀
D=−2B
⇀
D
时,在 ΔACD 中, AC=3 , CD=2√2 , ∠ACD=45 ∘ ,
| ⇀ | ;
∴AD2=AC2+CD2−2AC⋅CDcos45 ∘=5⇒ AD =√5
(ii) 当
C
⇀
D=2B
⇀
D
时,在 ΔACD 中, AC=3 , CD=6√2 , ∠ACD=45 ∘ ,
| ⇀ | .
∴AD2=AC2+CD2−2AC⋅CDcos45 ∘=45⇒ AD =3√5
17. 因为四边形 是边长为 的正方形,所以 ⃗ ⃗ , ⃗ ⃗ .
(1) ABCD 1
AB⋅AD=0 |AB|=|AD|=1
⃗ 2 ⃗ ⃗ 2 ⃗ ⃗
已知AP= AC,且
A
⃗
C=A
⃗
B+A
⃗
D
,则AP= (AB+AD).
5 5
⃗ ⃗ ⃗ 2 ⃗ ⃗ ⃗ 2 ⃗ 3 ⃗
那么DP=AP−AD= (AB+AD)−AD= AB− AD.
5 5 5
⃗ ⃗ ⃗ 2 ⃗ ⃗ ⃗ 3 ⃗ 2 ⃗
BP=AP−AB= (AB+AD)−AB=− AB+ AD.
5 5 5
⃗ ⃗ 2 ⃗ 3 ⃗ 3 ⃗ 2 ⃗
所以DP⋅BP=( AB− AD)⋅(− AB+ AD)
5 5 5 5
根据向量数量积的分配律展开可得:
⃗ ⃗ 2 ⃗ 3 ⃗ 2 ⃗ 2 ⃗ 3 ⃗ 3 ⃗ 3 ⃗ 2 ⃗
DP⋅BP= AB⋅(− AB)+ AB⋅ AD− AD⋅(− AB)− AD⋅ AD.
5 5 5 5 5 5 5 5
由于 ⃗ ⃗ ,且 ⃗ ⃗ , ⃗ ⃗ ,则:
AB⋅AD=0 AB2=|AB|2=1 AD2=|AD|2=1
⃗ ⃗ 6 ⃗ 6 ⃗ 6 6 12
DP⋅BP=− AB2+0+0− AD2=− − =− .
25 25 25 25 25
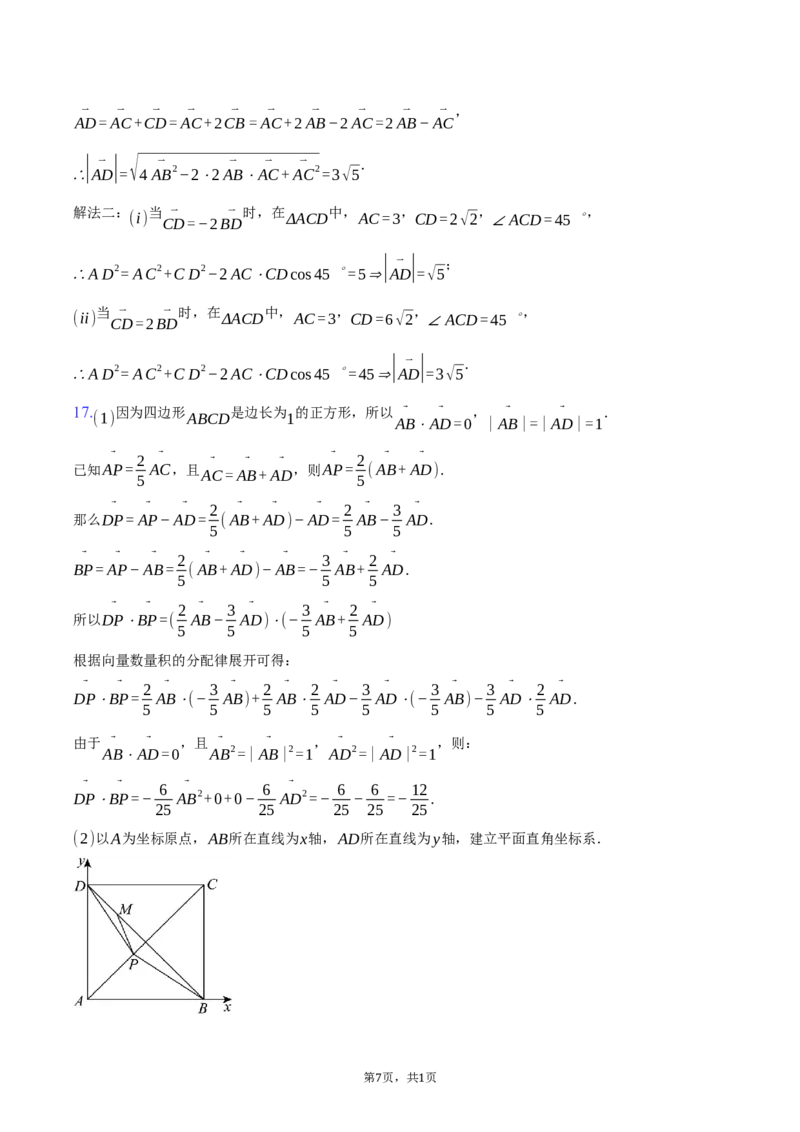
(2)以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立平面直角坐标系.
第 页,共 页
7 1则 , , , , ⃗ .
A(0,0) B(1,0) D(0,1) C(1,1) AC=(1,1)
⃗ 2 ⃗ ⃗ 2 2 2 2
因为AP= AC,所以AP=( , ),则P( , ).
5 5 5 5 5
设M(x,y),因为点M在直线BD上,直线BD的方程为x+ y=1(0≤x≤1),即y=1−x,所以
M(x,1−x).
⃗ 2 2 2 3 ⃗
则MP=( −x, −(1−x))=( −x,x− ), MB=(1−x,x−1) .
5 5 5 5
⃗ ⃗ 2 3
所以MP⋅MB=( −x)(1−x)+(x− )(x−1)
5 5
⃗ ⃗ 2 3 2 3
展开可得MP⋅MB=( −x)(1−x)−(x− )(1−x)=(1−x)[( −x)−(x− )]=(1−x)(1−2x).
5 5 5 5
进一步展开得
M
⃗
P⋅M
⃗
B=2x2−3x+1
,令 f(x)=2x2−3x+1(0≤x≤1) .
3 3 3 3 1 1
所以f(x)在x= 处取得最小值,f( )=2×( ) 2−3× +1=− ,即 ⃗ ⃗ 的最小值为− .
4 4 4 4 8
MP⋅MB
8
(3)总结常用的求数量积的方法以及每个方法适用范围:
定义法:⃗ ⃗ ⃗ ⃗ 为 与 的夹角 适用范围:已知向量的模长和夹角时,可直接使用
a⋅b=|a|×|b|×cosθ(θ ⃗a ⃗b ).
定义求数量积.
坐标法:若⃗ ,⃗ ,则⃗ ⃗ 适用范围:当向量的起点在坐标原点,或者
a=(x ,y ) b=(x ,y ) a⋅b=x x + y y .
1 1 2 2 1 2 1 2
可以通过建立平面直角坐标系方便地得到向量的坐标时,使用坐标法较为简便.
基底法:将所求向量用已知向量表示出来,然后根据向量数量积的运算律进行计算.适用范围:在一些几何
图形中,已知一些向量的关系,通过向量的加减法、数乘等线性运算将未知向量转化为已知向量,进而求
数量积.
其他方法:极化恒等式,适用于共点的数量积问题,求最值小题使用比较快;投影法,对于几何问题,投
影固定或者模长固定,比较好用.
18.(1)∵asinB=bsin2A,∴sinAsinB=sinBsin2A,即sinAsinB=2sinAcosAsinB,
∵A,B∈(0,π),∴sinA≠0,sinB≠0,
1 π
∴cosA= ,故A= .
2 3
√3
(2)由(1)得,sin A= ,
2
第 页,共 页
8 11 3√3
∵▵ABC的面积为3√3,∴ bcsin A=3√3,即 c=3√3,解得c=4,
2 4
1
由余弦定理得,a2=b2+c2−2bccosA=9+16−2×3×4× =13,
2
∴a=√13,故▵ABC的周长为7+√13.
π 2π 2π
(3)由A= 得B+C= ,则C= −B,
3 3 3
(2π ) 1 √3
∴2cosB+cosC=2cosB+cos −B =2cosB− cosB+ sinB
3 2 2
√3 3 ( π).
= sinB+ cosB=√3sin B+
2 2 3
π 2π π π π
∵▵ABC为锐角三角形,∴0