文档内容
格致课堂
8.4.2 空间点、直线、平面之间的位置关系
一、选择题
1.如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为
A.相交 B.平行 C.异面而且垂直 D.异面但不垂直
【答案】D
【解析】利用展开图可知,线段AB与CD是正方体中的相邻两个面的面对角线,仅仅异面,所成的角为
600,因此选D
2.若直线 ,直线 ,则直线a与b的位置关系是( )
A.相交 B.异面 C.异面或平行 D.平行
【答案】C
【解析】由题意直线a∥α,直线b α,可得直线a,b一定没有公共点,故两直线的位置关系可以是异面
或平行 ⊂
故选C.
3.如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系一定是( )
A.平行 B.相交
C.平行或相交 D.不能确定
【答案】C
【解析】
如下图所示:由图可知,两个平面平行或相交,故选C.
4.已知平面α和直线l,则α内至少有一条直线与l( )格致课堂
A.异面 B.相交 C.平行 D.垂直
【答案】D
【解析】若直线l∥α,α内至少有一条直线与l垂直,
当l与α相交时,α内至少有一条直线与l垂直.
当l α,α内至少有一条直线与l垂直.
故选⊂D.
5.(多选题)已知 表示不同的点, 表示直线, 表示不同的平面,则下列推理正确的是
( )
A. , , ,
B. , , ,
C. ,
D. , ,
【答案】ABD
【解析】
【分析】对于选项A:由公理1知, ,故选项A正确;
对于选项B:因为 表示不同的平面,由公理3知,平面 相交,且 ,故选项B正确;
对于选项C: 分两种情况: 与 相交或 .当 与 相交时,若交点为A,则 ,故选项C错误;
对于选项D:由公理1逆推可得结论成立,故选项D成立;
故选:ABD
6.(多选题)如图所示,在正方体 中, 分别为棱 的中点,则以下四
个结论正确的是( )格致课堂
A.直线 与 是相交直线 B.直线 与 是平行直线
C.直线 与 是异面直线 D.直线 与 是异面直线
【答案】CD
【解析】直线 与 是异面直线,直线 与 也是异面直线,故A、B错误
直线 与 是异面直线,直线 与 是异面直线,故C、D正确.
故选CD.
二、填空题
7.以下四个命题中, 正确命题的个数是_________.
①不共面的四点中,其中任意三点不共线;
②若点A,B,C,D共面,点A, B,C,E共面,则点A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
【答案】1
【解析】正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;②从条
件看出两平面有三个公共点A、B、C,但是若A、B、C共线,则结论不正确;③不正确,共面不具有传
递性,若直线a、b共面,直线a、c共面,则直线b、c可能异面;④不正确,因为此时所得的四边形四条
边可以不在一个平面上,空间四边形的四个定点就不共面.
故答案为:1.
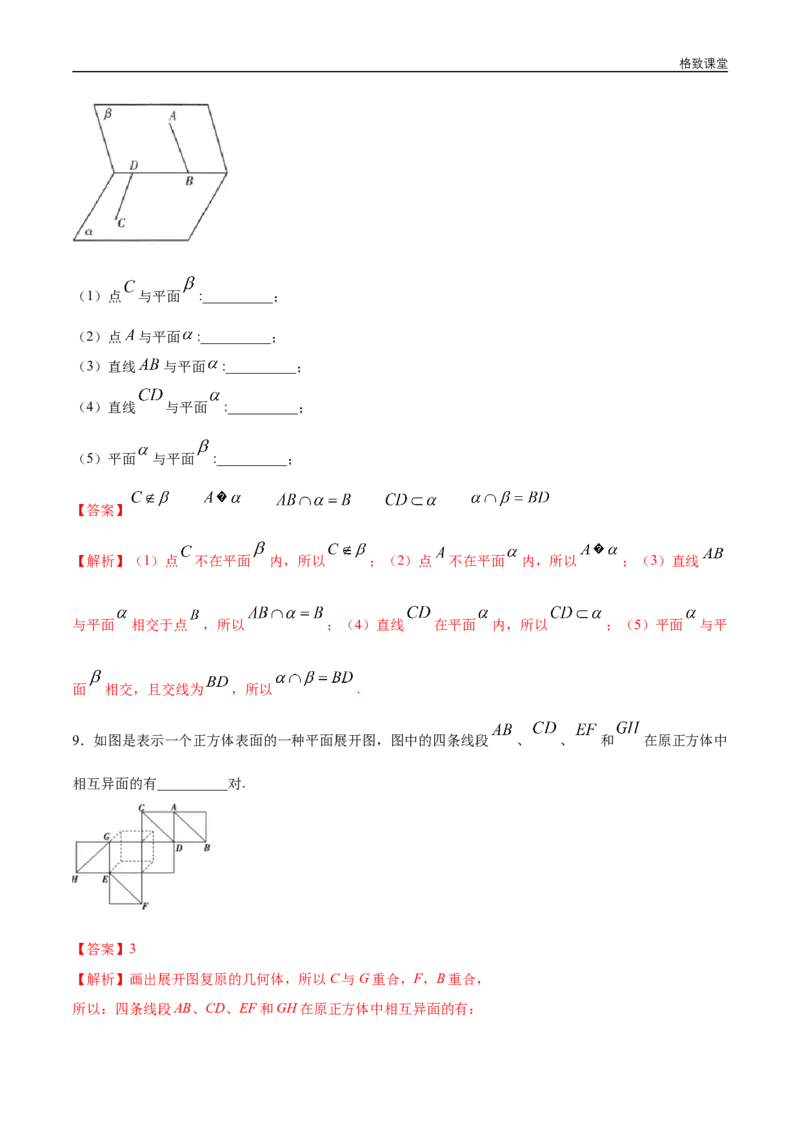
8.如图,试用适当的符号表示下列点、直线和平面之间的关系:格致课堂
(1)点 与平面 :__________;
(2)点 与平面 :__________;
(3)直线 与平面 :__________;
(4)直线 与平面 :__________;
(5)平面 与平面 :__________;
【答案】
【解析】(1)点 不在平面 内,所以 ;(2)点 不在平面 内,所以 ;(3)直线
与平面 相交于点 ,所以 ;(4)直线 在平面 内,所以 ;(5)平面 与平
面 相交,且交线为 ,所以 .
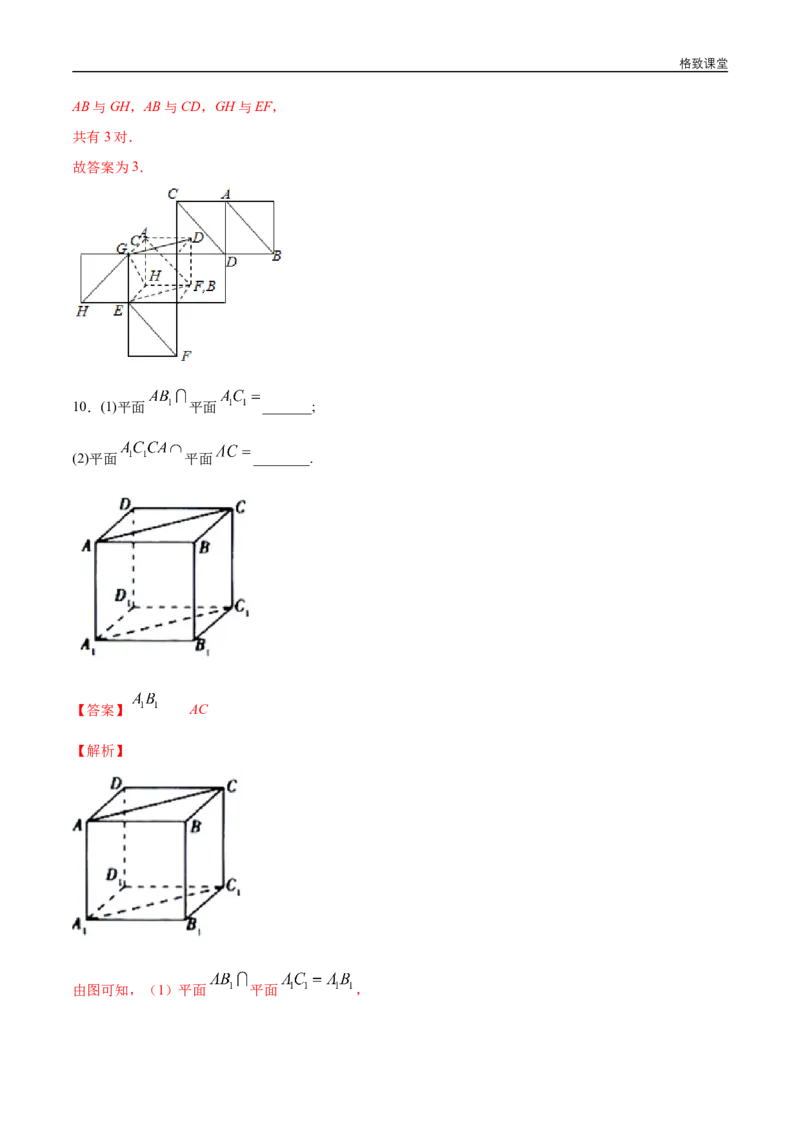
9.如图是表示一个正方体表面的一种平面展开图,图中的四条线段 、 、 和 在原正方体中
相互异面的有__________对.
【答案】3
【解析】画出展开图复原的几何体,所以C与G重合,F,B重合,
所以:四条线段AB、CD、EF和GH在原正方体中相互异面的有:格致课堂
AB与GH,AB与CD,GH与EF,
共有3对.
故答案为3.
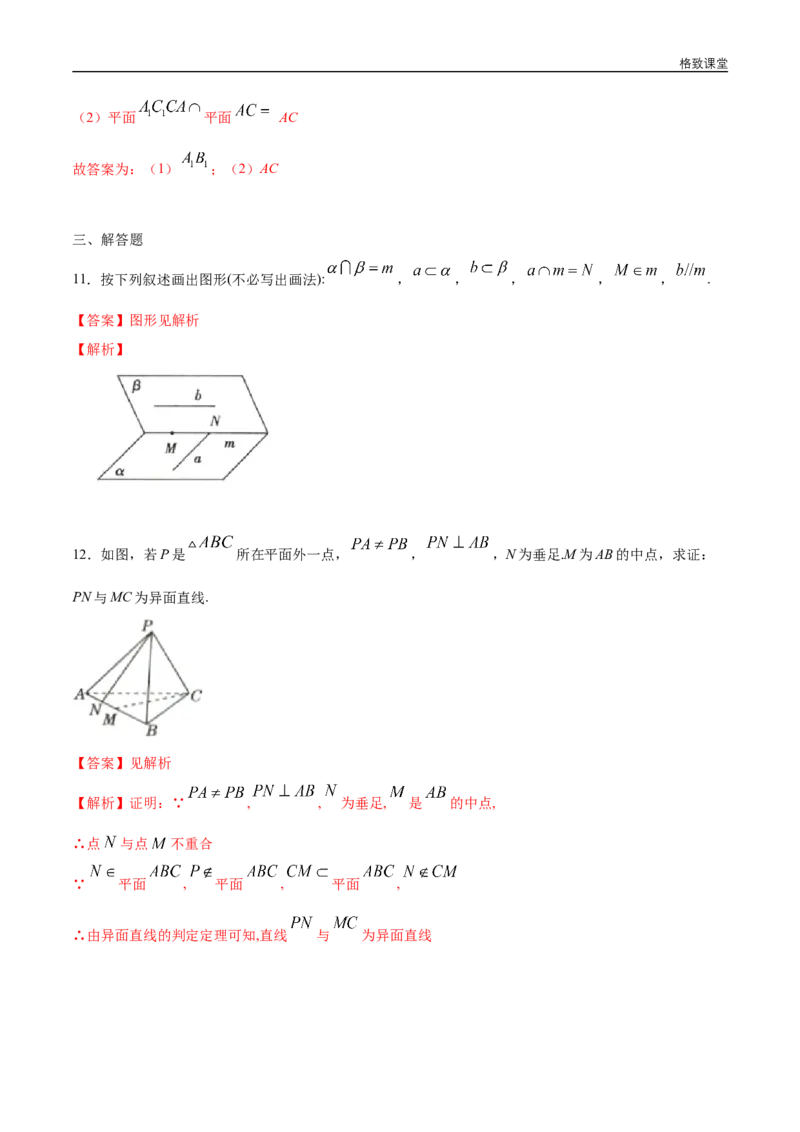
10.(1)平面 平面 _______;
(2)平面 平面 ________.
【答案】 AC
【解析】
由图可知,(1)平面 平面 ,格致课堂
(2)平面 平面 AC
故答案为:(1) ;(2)AC
三、解答题
11.按下列叙述画出图形(不必写出画法): , , , , , .
【答案】图形见解析
【解析】
12.如图,若P是 所在平面外一点, , ,N为垂足.M为AB的中点,求证:
PN与MC为异面直线.
【答案】见解析
【解析】证明:∵ , , 为垂足, 是 的中点,
∴点 与点 不重合
∵ 平面 , 平面 , 平面 ,
∴由异面直线的判定定理可知,直线 与 为异面直线格致课堂