文档内容
格致课堂
8.5.2 直线与平面平行
第 2 课时 直线与平面平行的性质
一、选择题
1.已知直线l和平面α,若 , ,则过点P且平行于l的直线( )
A.只有一条,不在平面α内
B.只有一条,且在平面α内
C.有无数条,一定在平面α内
D.有无数条,一定不在平面α内
【答案】B
【解析】假设过点P且平行于 的直线有两条 与 ,∴ 且 ,
由平行公理得 ,这与两条直线 与 相交与点 相矛盾.
故选:B.
2.如图,在长方体 中, 、 分别是棱 和 的中点,过 的平面 分
别交 和 于点 、 ,则 与 的位置关系是( )
A.平行 B.相交 C.异面 D.平行或异面
【答案】A
【解析】在长方体 中, , 、 分别为 、 的中点, ,
四边形 为平行四边形, ,
平面 , 平面 , 平面 ,
平面 ,平面 平面 , ,格致课堂
又 , ,故选A.
3.如图,在三棱柱ABC-ABC 中,AM=2MA ,BN=2NB ,过MN作一平面交底面三角形ABC的边
1 1 1 1 1
BC、AC于点E、F,则 ( )
A.MF∥NE
B.四边形MNEF为梯形
C.四边形MNEF为平行四边形
D.AB∥NE
1 1
【答案】B
【解析】
∵在 AABB中,AM=2MA ,BN=2NB ,∴AM//BN,∴MN//AB.
1 1 1 1
又MN 平面ABC,AB 平面ABC,
∴MN∥⊄平面ABC. ⊂
又MN 平面MNEF,平面MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB,
显然在⊂△ABC中EF≠AB,∴EF≠MN,∴四边形MNEF为梯形.故选B.
4.如图,四棱锥S-ABCD的所有棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点
F,则四边形DEFC的周长为 ( )
A.2+ B.3+ C.3+2 D.2+2
【答案】C
【解析】因为AB=BC=CD=DA=2,所以四边形ABCD是菱形,所以CD∥AB,
又CD 平面SAB,AB 平面SAB,所以CD∥平面SAB.
又CD⊄平面CDEF,平⊂面CDEF∩平面SAB=EF,所以CD∥EF,
⊂格致课堂
所以EF∥AB.又因为E为SA中点,所以EF= AB=1.
又因为△SAD和△SBC都是等边三角形,所以DE=CF=2×sin60°= ,
所以四边形DEFC的周长为:CD+DE+EF+FC=3+2 .故选C.
5.(多选题)在梯形 中, , 平面 , 平面 ,则直线 与平面 内的
直线的位置关系只能是( )
A.平行 B.异面 C.相交 D.共面
【答案】AB
【解析】
∵ , 平面 , 平面 ,∴ 平面 ,∴直线 与平面 内的直线没有公共
点,直线 与平面 内的直线的位置关系可能平行,也可能异面,故选A .
6.(多选题)在空间四边形 中, 分别是 上的点,当 平面 时,
下面结论正确的是( )
A. 一定是各边的中点
B. 一定是 的中点
C. ,且
D.四边形 是平行四边形或梯形
【答案】CD
【解析】由 平面 ,所以由线面平行的性质定理,得 , ,则 ,
且 ,且 ,四边形 是平行四边形或梯形.
故选: .格致课堂
二、填空题
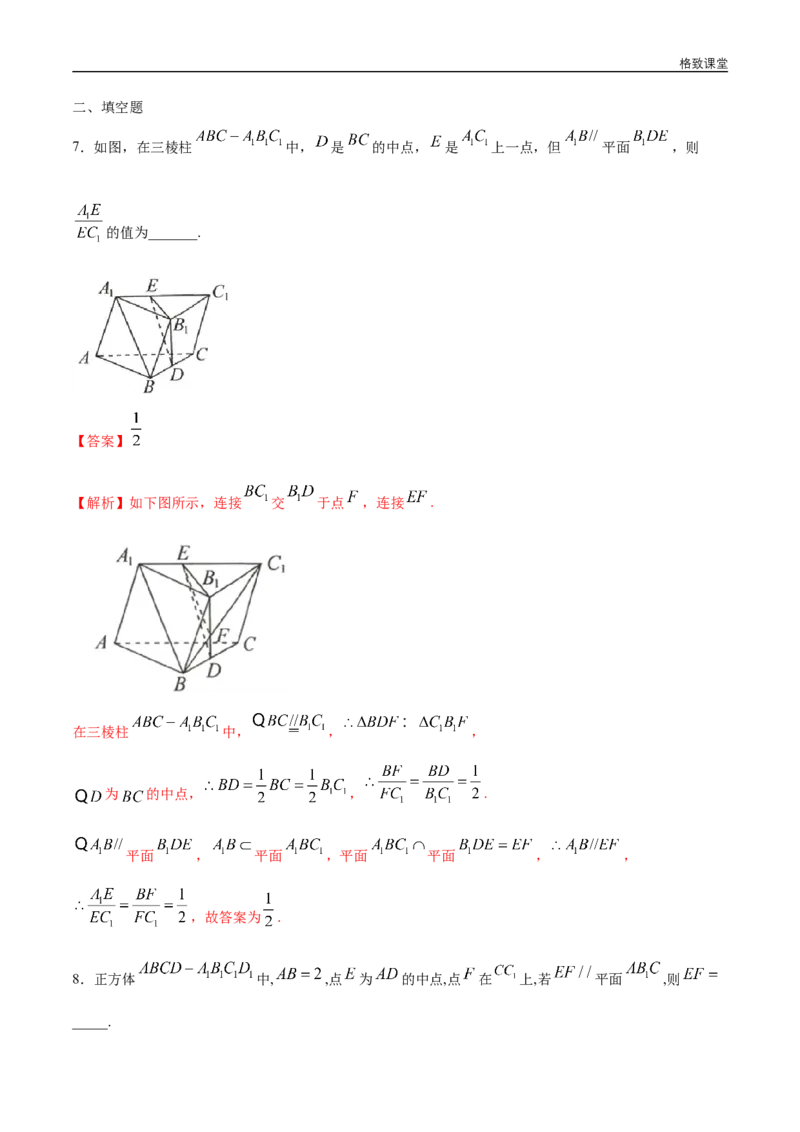
7.如图,在三棱柱 中, 是 的中点, 是 上一点,但 平面 ,则
的值为_______.
【答案】
【解析】如下图所示,连接 交 于点 ,连接 .
在三棱柱 中, , ,
为 的中点, , .
平面 , 平面 ,平面 平面 , ,
,故答案为 .
8.正方体 中, ,点 为 的中点,点 在 上,若 平面 ,则
_____.格致课堂
【答案】
【解析】取 中点 ,连接
为 的中点, 为 中点 平面
又因为: 平面
平面 平面 平面 ,
因为 平面 平面 平面
为 中点.
在 中,计算知:
故答案为
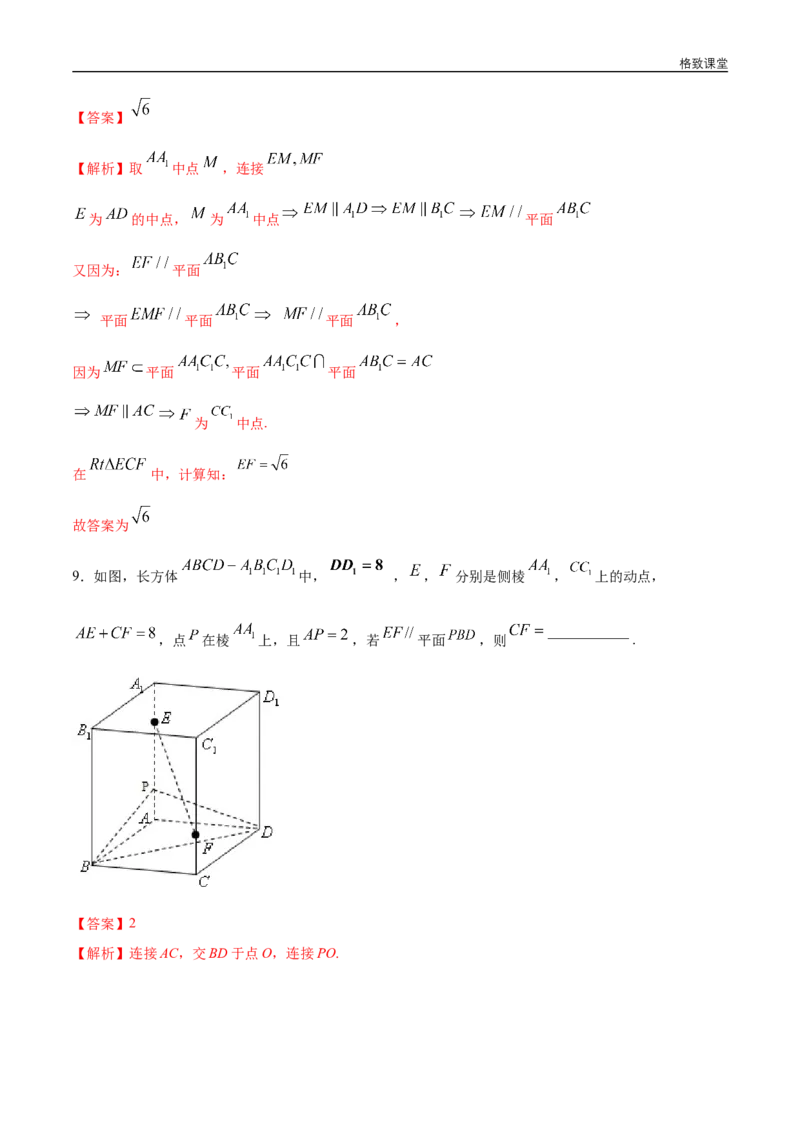
9.如图,长方体 中, , , 分别是侧棱 , 上的动点,
,点 在棱 上,且 ,若 平面 ,则 .
【答案】2
【解析】连接AC,交BD于点O,连接PO.格致课堂
因为 平面PBD, 平面 ,平面 平面 ,所以 ;在 上截
取 ,连接 ,则 ,所以 ,
所以易知四边形 为平行四边形,则 .
又 , ,所以 ,故 .
故答案为: .
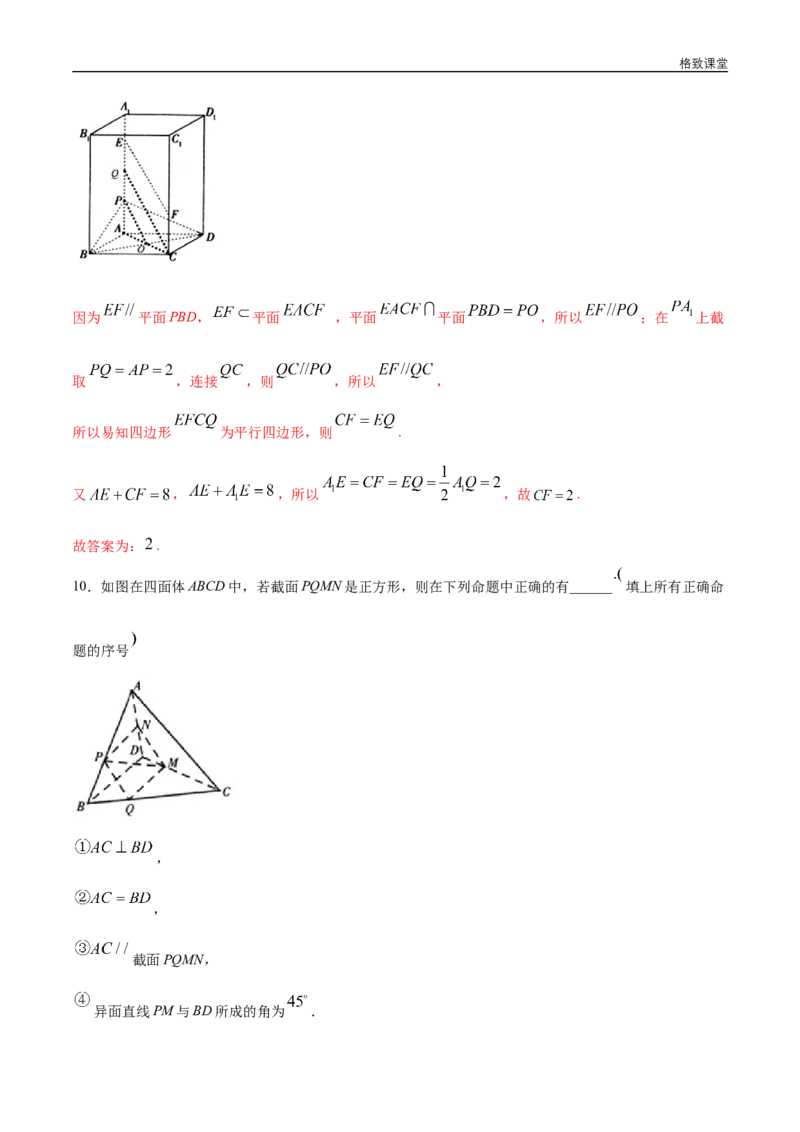
10.如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有______ 填上所有正确命
题的序号
,
,
截面PQMN,
异面直线PM与BD所成的角为 .格致课堂
【答案】
【解析】解:在四面体 中, 截面 是正方形, , 平面 ,
平面 , 平面 .
平面 平面 , ,可得 平面 .
同理可得 平面 , .
, .
由 ,
是异面直线 与 所成的角,且为 .
由上面可知: , .
, ,
而 , ,
.
综上可知: 都正确.
故答案为 .
利用线面平行与垂直的判定定理和性质定理、正方形的性质、异面直线所成的角即可得出.
三、解答题
11.如图所示, 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD 平面
PBC= .格致课堂
(1)求证:BC∥ ;
(2)MN与平面PAD是否平行?试证明你的结论.
【答案】(1)见解析;(2)见解析
【解析】(1)证明 因为BC∥AD,AD 平面PAD,
BC 平面PAD,所以BC∥平面PAD.⊂
又平⊄面PAD∩平面PBC=l,BC 平面PBC,所以BC∥l.
(2)解 MN∥平面PAD.证明如下⊂:
如图所示,取PD中点E,连结AE,EN.
又∵N为PC的中点,∴
又∵
∴
即四边形AMNE为平行四边形.
∴AE∥MN,又MN 平面PAD,AE 平面PAD
.∴MN∥平面PAD. ⊄ ⊂
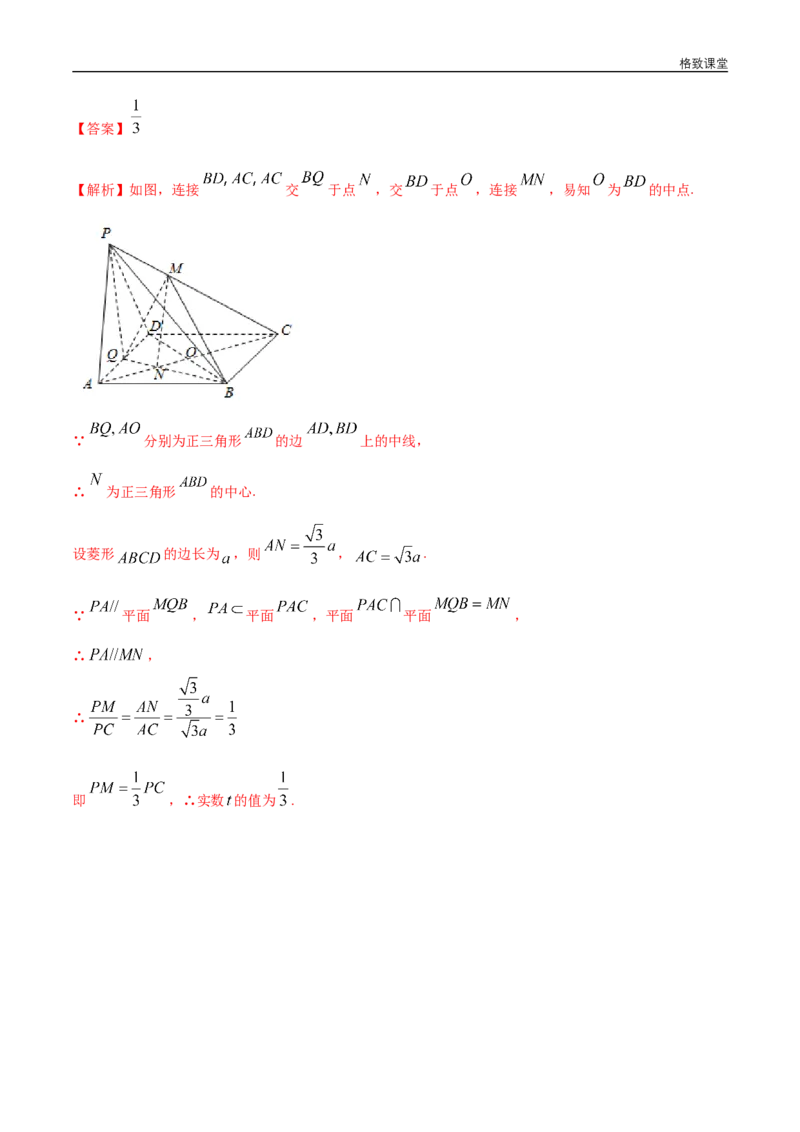
12.如图,在四棱锥 中,底面 为菱形, , 为 的中点,点 在侧棱
上,且 ,若 平面 ,试确定实数 的值.格致课堂
【答案】
【解析】如图,连接 交 于点 ,交 于点 ,连接 ,易知 为 的中点.
∵ 分别为正三角形 的边 上的中线,
∴ 为正三角形 的中心.
设菱形 的边长为 ,则 , .
∵ 平面 , 平面 ,平面 平面 ,
∴ ,
∴
即 ,∴实数 的值为 .