文档内容
格致课堂
8.5.3 平面与平面平行
第2课时 平面与平面平行的性质
(用时45分钟)
【选题明细表】
知识点、方法 题号
面面平行的性质 1,2,4
面面平行的性质的应用 3,5,6,7,9
综合应用 8,10,11,12
基础巩固
1.已知直线 ,两个不重合的平面 .若 // , ,则下列四个结论中正确的是( )
① 与 内的所有直线平行; ② 与 内的无数条直线平行;
③ 与 内任何一条直线都不垂直; ④ 与 没有公共点.
A.①② B.②④ C.②③ D.③④
【答案】B
【解析】由面面平行的性质知①错误;
由面面平行的性质知②正确;
与 内的直线可能异面垂直,故③错;
由面面平行的定义知④正确.
故选:B
2.设平面 , , , 是 的中点,当点 分别在平面 内运动时,则所有的动
点 ( )
A.不共面
B.当且仅当 分别在两条直线上移动时才共面
C.当且仅当 分别在两条给定的异面直线上移动时才共面格致课堂
D.不论 如何移动,都共面
【答案】D
【解析】如图所示,记 , 分别是 , 两点在 , 上运动后的两点,此时 中点变成 中点
.
连结 ,取 中点 ,连结 , , , , ,则 ,
从而易得 .同理 .
∵ ,
∴ .
∵ ,
∴平面 平面 ,
∴ 平面 .
故无论 , 如何移动,所有的动点 都在过点 且与 , 都平行的平面上.
故选D.
3.如图,在多面体 中,平面 平面 ,且 ,
则 ( )格致课堂
A. 平面 B. 平面
C. D.平面 平面
【答案】A
【解析】如图所示,取DG的中点M,连AM、FM,.
则由已知条件易证得四边形DEFM是平行四边形,
∴ 且 .
∵平面ABC∥平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,
∴AB∥DE,
∴AB∥FM.
又AB=DE,
∴AB=FM,
∴四边形ABFM是平行四边形,
∴BF∥AM.
又BF 平面ACGD,AM 平面ACGD,
∴BF∥平面ACGD.选A.
4.两个平行平面与另两个平行平面相交所得四条直线的位置关系是( )
A.两两相互平行
B.两两相交于一点
C.两两相交但不一定交于同一点
D.两两相互平行或交于同一点
【答案】A
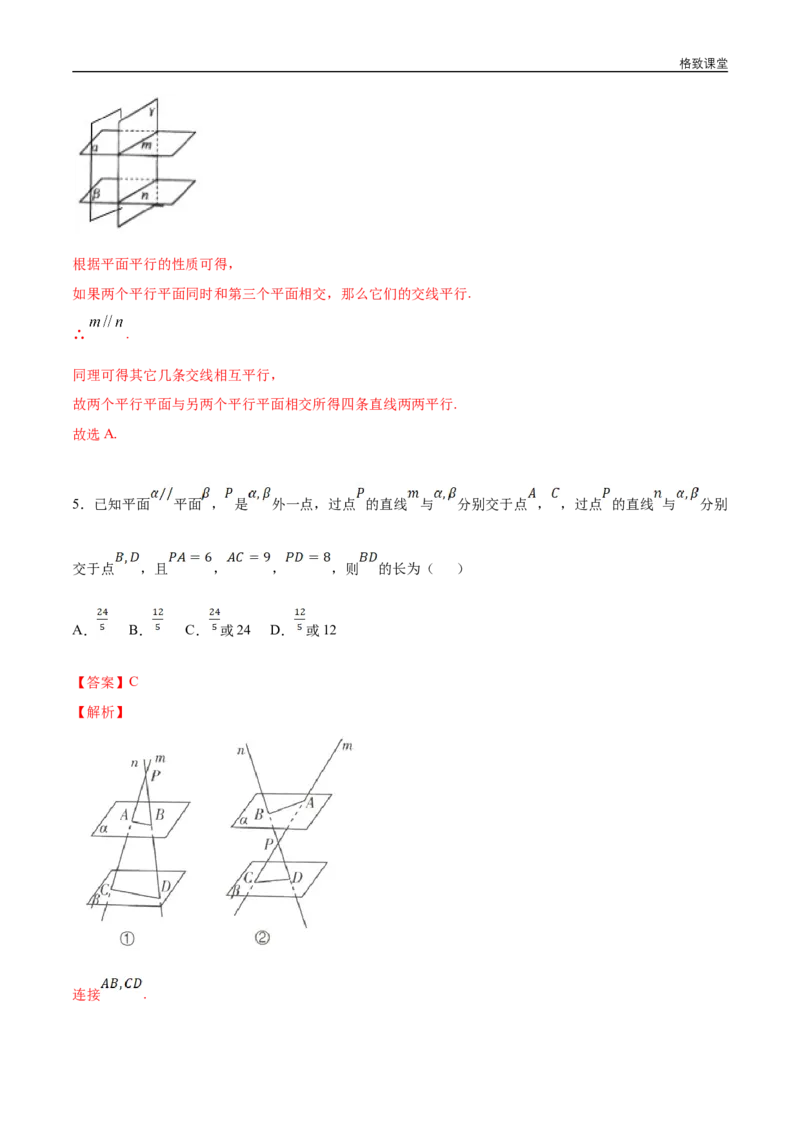
【解析】根据题意,作图如下: , , ,格致课堂
根据平面平行的性质可得,
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
∴ .
同理可得其它几条交线相互平行,
故两个平行平面与另两个平行平面相交所得四条直线两两平行.
故选A.
5.已知平面 平面 , 是 外一点,过点 的直线 与 分别交于点 , ,过点 的直线 与 分别
交于点 ,且 , , ,则 的长为( )
A. B. C. 或24 D. 或12
【答案】C
【解析】
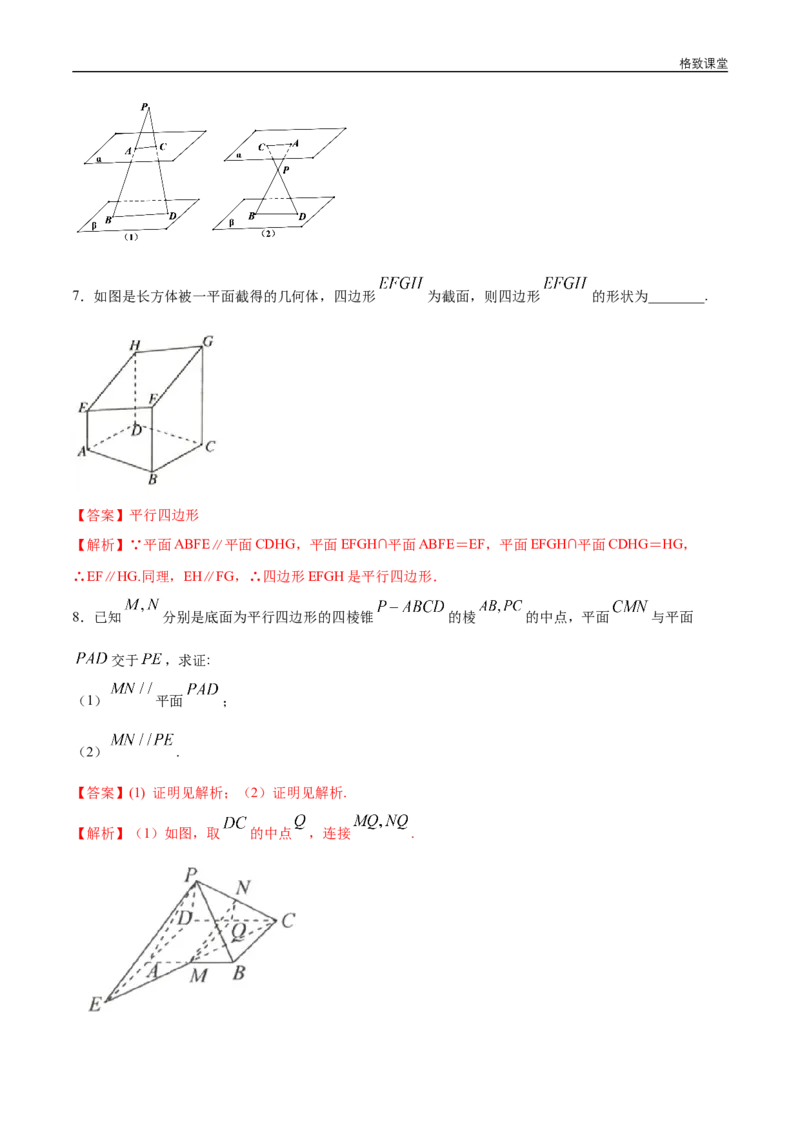
连接 .格致课堂
(1)当点 在 的延长线上,即 在平面 与平面 的同侧时,如图①;
∵ ,平面 ,平面 ,
∴ ,∴ .
∵ ,
∴ ,记得 .
(2)当点 在线段 上,即 在平面 与平面 之间时,如图②.
类似(1)的方法,可得 .
∵ ,
∴ ,解得 ,
∴ .
综上, 的长为 或24.
故选C
6.过两平行平面α、β外的点P两条直线AB与CD,它们分别交α于A、C两点,交β于B、D两点,若
PA=6,AC=9,PB=8,则BD的长为_______.
【答案】12
【解析】当两个平面在点P的同侧时如图(1)所示,当点P在两个面的中间时如图(2)所示由面面平行
的性质定理可得AC与BD平行, ,所以 .格致课堂
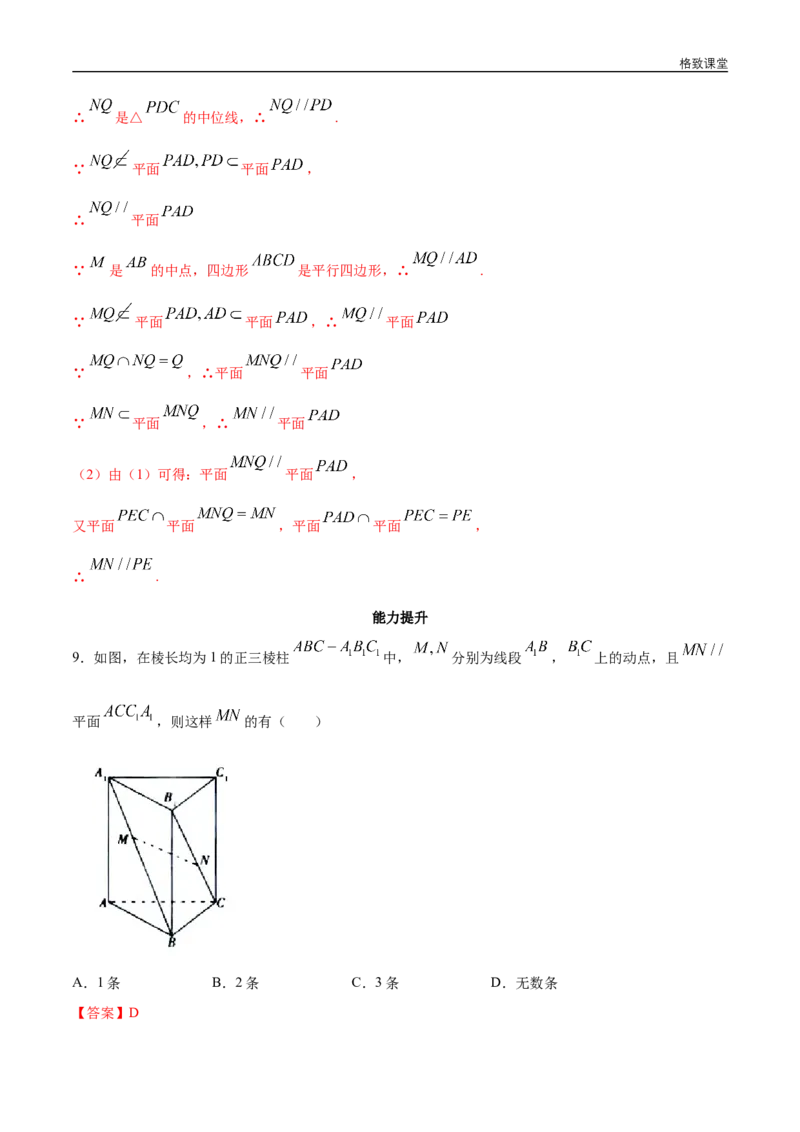
7.如图是长方体被一平面截得的几何体,四边形 为截面,则四边形 的形状为________.
【答案】平行四边形
【解析】∵平面ABFE∥平面CDHG,平面EFGH∩平面ABFE=EF,平面EFGH∩平面CDHG=HG,
∴EF∥HG.同理,EH∥FG,∴四边形EFGH是平行四边形.
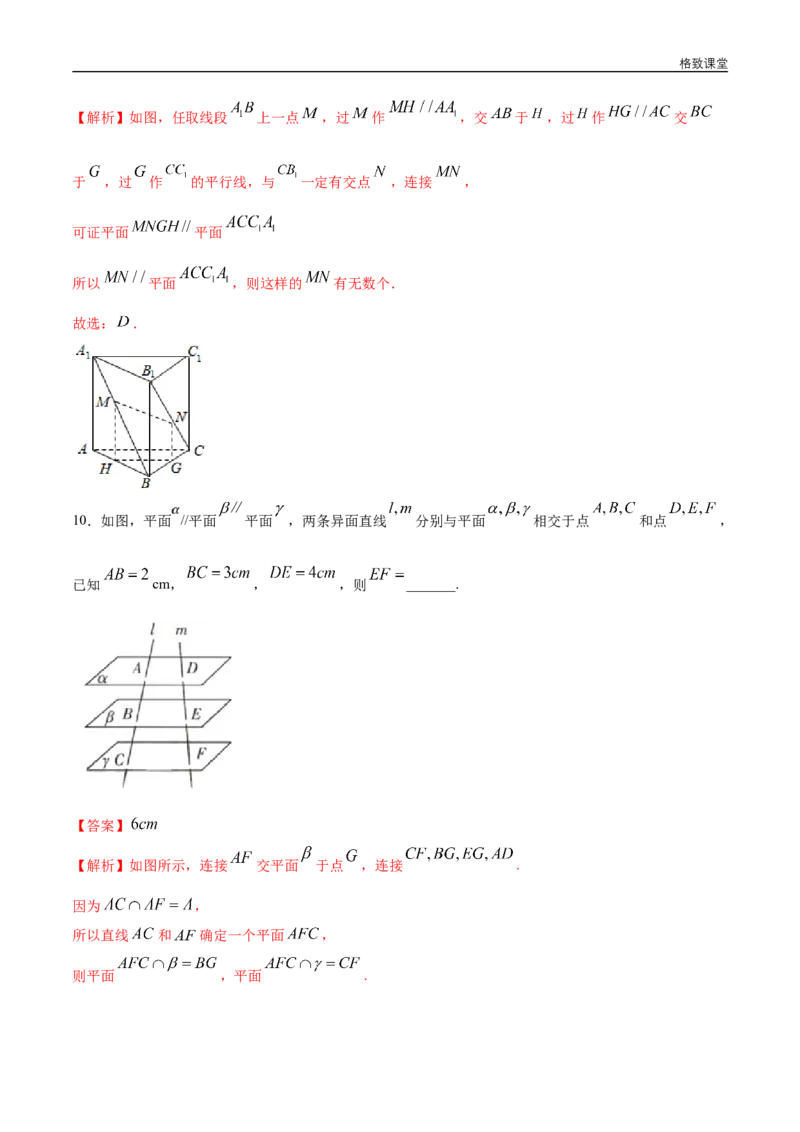
8.已知 分别是底面为平行四边形的四棱锥 的棱 的中点,平面 与平面
交于 ,求证:
(1) 平面 ;
(2) .
【答案】(1) 证明见解析;(2)证明见解析.
【解析】(1)如图,取 的中点 ,连接 .格致课堂
∴ 是△ 的中位线,∴ .
∵ 平面 平面 ,
∴ 平面
∵ 是 的中点,四边形 是平行四边形,∴ .
∵ 平面 平面 ,∴ 平面
∵ ,∴平面 平面
∵ 平面 ,∴ 平面
(2)由(1)可得:平面 平面 ,
又平面 平面 ,平面 平面 ,
∴ .
能力提升
9.如图,在棱长均为1的正三棱柱 中, 分别为线段 , 上的动点,且
平面 ,则这样 的有( )
A.1条 B.2条 C.3条 D.无数条
【答案】D格致课堂
【解析】如图,任取线段 上一点 ,过 作 ,交 于 ,过 作 交
于 ,过 作 的平行线,与 一定有交点 ,连接 ,
可证平面 平面
所以 平面 ,则这样的 有无数个.
故选: .
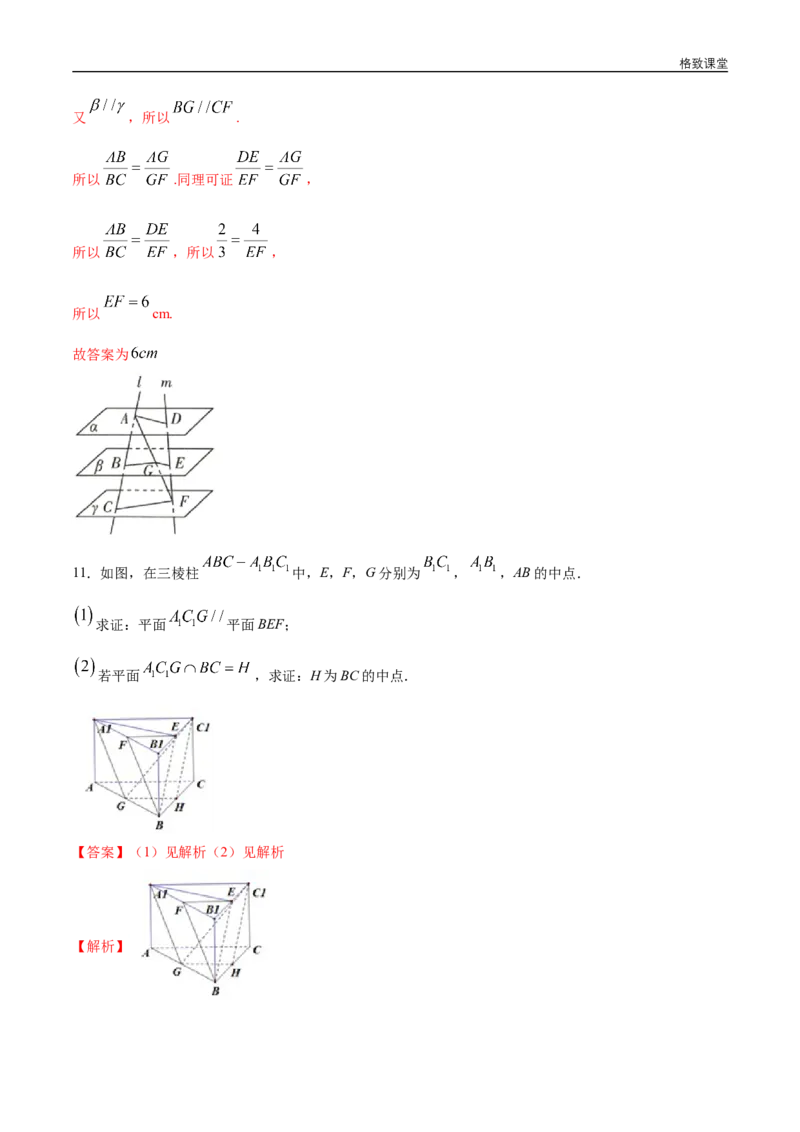
10.如图,平面 //平面 平面 ,两条异面直线 分别与平面 相交于点 和点 ,
已知 cm, , ,则 _______.
【答案】
【解析】如图所示,连接 交平面 于点 ,连接 .
因为 ,
所以直线 和 确定一个平面 ,
则平面 ,平面 .格致课堂
又 ,所以 .
所以 .同理可证 ,
所以 ,所以 ,
所以 cm.
故答案为
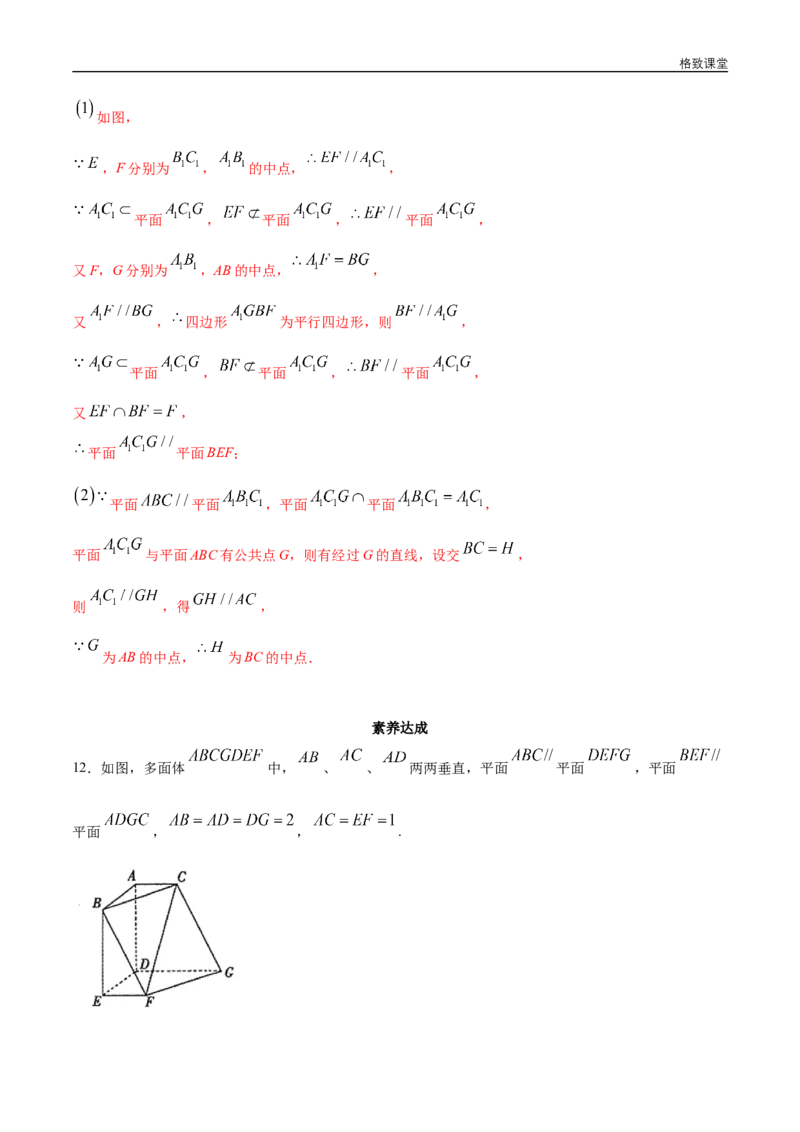
11.如图,在三棱柱 中,E,F,G分别为 , ,AB的中点.
求证:平面 平面BEF;
若平面 ,求证:H为BC的中点.
【答案】(1)见解析(2)见解析
【解析】格致课堂
如图,
,F分别为 , 的中点, ,
平面 , 平面 , 平面 ,
又F,G分别为 ,AB的中点, ,
又 , 四边形 为平行四边形,则 ,
平面 , 平面 , 平面 ,
又 ,
平面 平面BEF;
平面 平面 ,平面 平面 ,
平面 与平面ABC有公共点G,则有经过G的直线,设交 ,
则 ,得 ,
为AB的中点, 为BC的中点.
素养达成
12.如图,多面体 中, 、 、 两两垂直,平面 平面 ,平面
平面 , , .格致课堂
(1)证明:四边形 是正方形;
(2)判断点 、 、 、 是否共面,并说明理由.
【答案】(1)证明见解析;(2) 、 、 、 四点共面,理由见解析.
【解析】(1)因为平面 平面 ,平面 平面 ,平面 平面
,由面面平行的性质定理,得 ,同理 .
所以四边形 为平行四边形.
又 , ,所以平行四边形 是正方形;
(2)如图,取 的中点 ,连接 、 .
因为平面 平面 ,平面 平面 ,平面 平面 ,由
面面平行的性质定理,得 ,同理 ,
在梯形 中, ,且 为 的中点, , ,
, ,则四边形 为平行四边形, 且 .
又 , ,所以 且 ,
所以四边形 为平行四边形,所以 .
为 的中点, ,
又 , 四边形 为平行四边形, , .
故 、 、 、 四点共面.格致课堂