文档内容
格致课堂
8.6.1 直线与直线垂直
一、选择题
1.分别和两条异面直线相交的两条不同直线的位置关系是( )
A.相交 B.异面 C.异面或相交 D.平行
【答案】C
【解析】
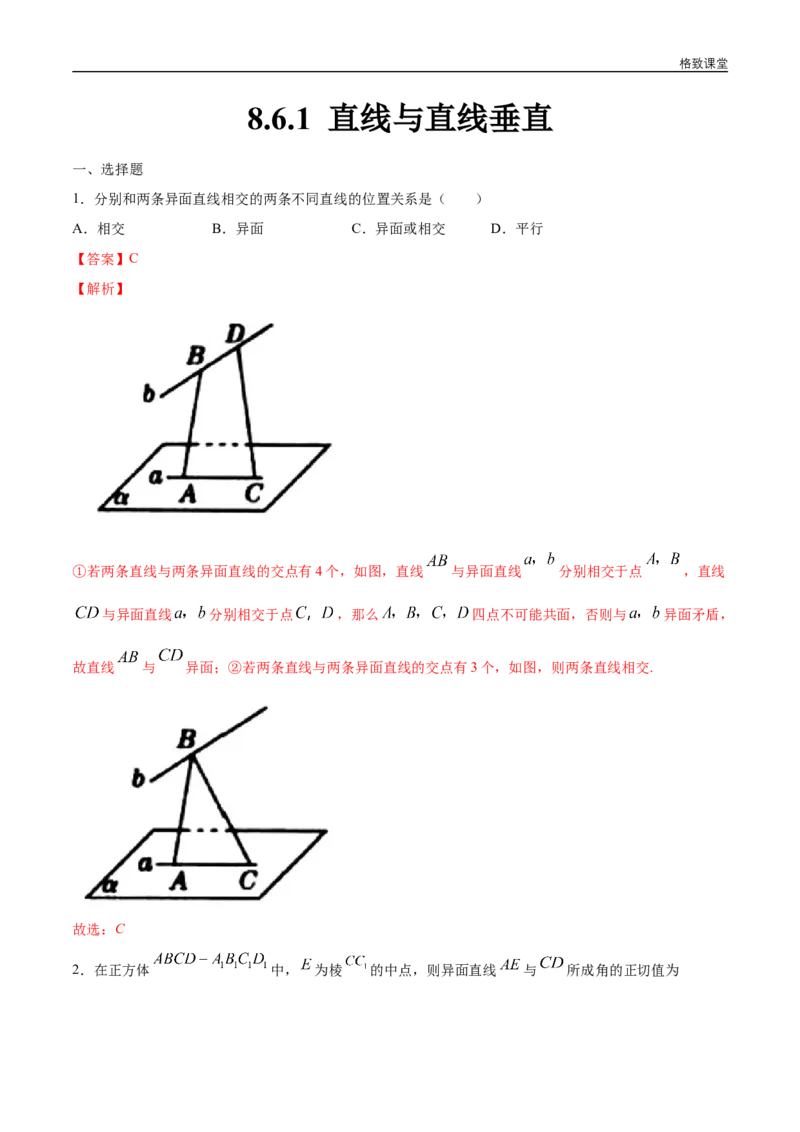
①若两条直线与两条异面直线的交点有4个,如图,直线 与异面直线 分别相交于点 ,直线
与异面直线 分别相交于点 ,那么 四点不可能共面,否则与 异面矛盾,
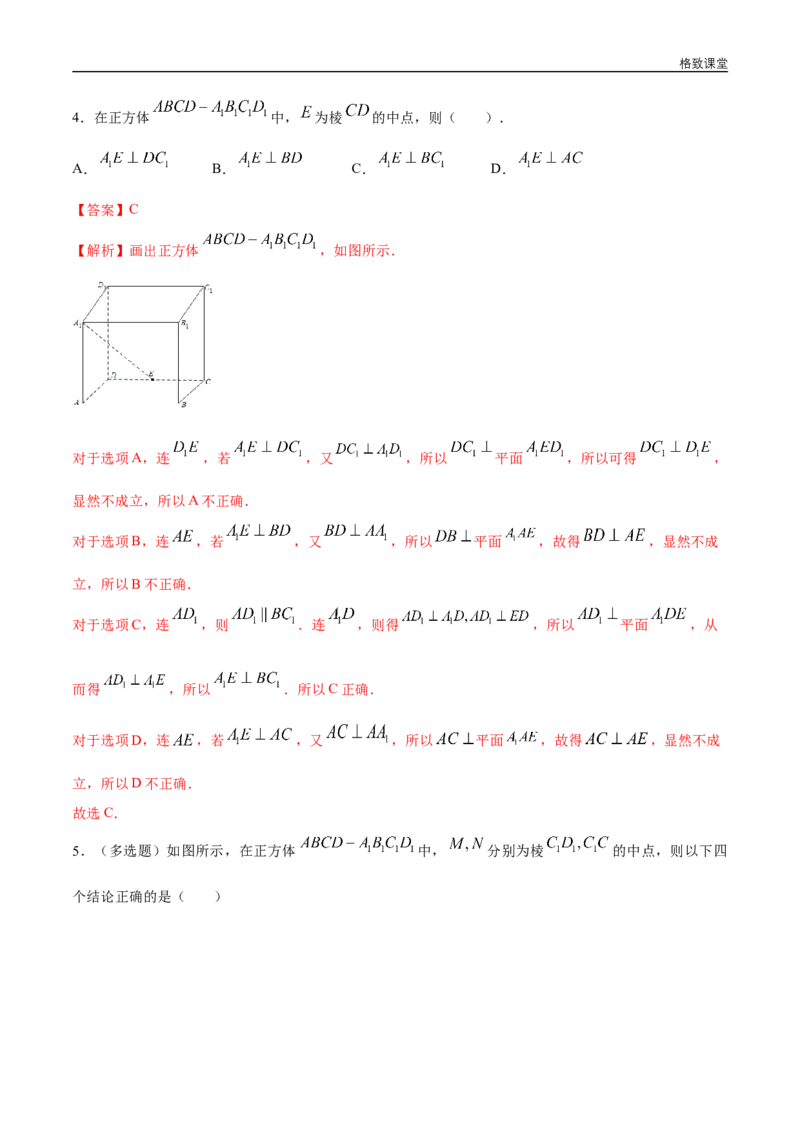
故直线 与 异面;②若两条直线与两条异面直线的交点有3个,如图,则两条直线相交.
故选:C
2.在正方体 中, 为棱 的中点,则异面直线 与 所成角的正切值为格致课堂
A. B. C. D.
【答案】C
【解析】在正方体 中, ,所以异面直线 与 所成角为 ,
设正方体边长为 ,则由 为棱 的中点,可得 ,所以 ,
则 .故选C.
3.已知直三棱柱 中, , , ,则异面直线 与
所成角的余弦值为( )
A. B. C. D.
【答案】C
【解析】如图所示,补成直四棱柱 ,
则所求角为 ,
易得 ,因此 ,故选C.格致课堂
4.在正方体 中, 为棱 的中点,则( ).
A. B. C. D.
【答案】C
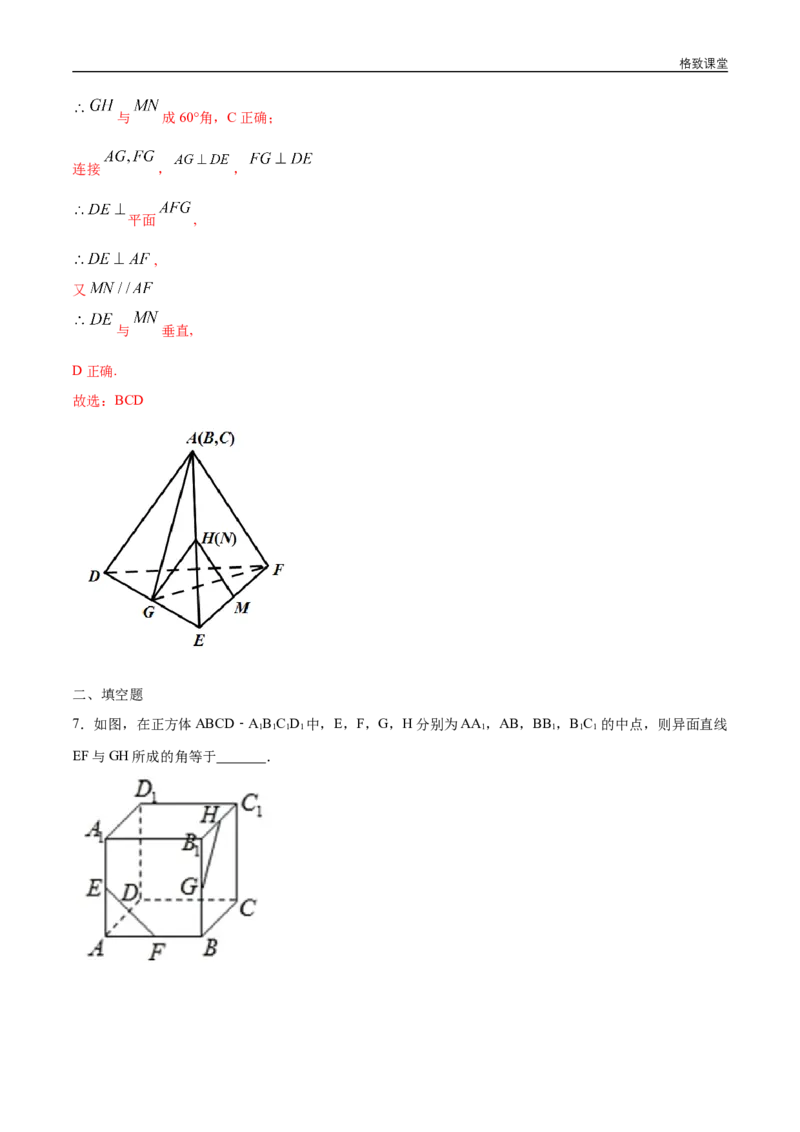
【解析】画出正方体 ,如图所示.
对于选项A,连 ,若 ,又 ,所以 平面 ,所以可得 ,
显然不成立,所以A不正确.
对于选项B,连 ,若 ,又 ,所以 平面 ,故得 ,显然不成
立,所以B不正确.
对于选项C,连 ,则 .连 ,则得 ,所以 平面 ,从
而得 ,所以 .所以C正确.
对于选项D,连 ,若 ,又 ,所以 平面 ,故得 ,显然不成
立,所以D不正确.
故选C.
5.(多选题)如图所示,在正方体 中, 分别为棱 的中点,则以下四
个结论正确的是( )格致课堂
A.直线 与 是相交直线 B.直线 与 是平行直线
C.直线 与 是异面直线 D.直线 与 是异面直线
【答案】CD
【解析】直线 与 是异面直线,直线 与 也是异面直线,故A、B错误
直线 与 是异面直线,直线 与 是异面直线,故C、D正确.
故选CD.
6.(多选题)如图所示是正四面体的平面展开图, 分别为 的中点,在这个正四面
体中,下列命题正确的是( )
A. 与 平行 B. 与 为异面直线
C. 与 成60°角 D. 与 垂直
【答案】BCD
【解析】如图,把平面展开图还原成正四面体,知 与 为异面直线,A不正确;
与 为异面直线,B正确;
, ,而 , ,格致课堂
与 成60°角,C正确;
连接 , ,
平面 ,
,
又
与 垂直,
D正确.
故选:BCD
二、填空题
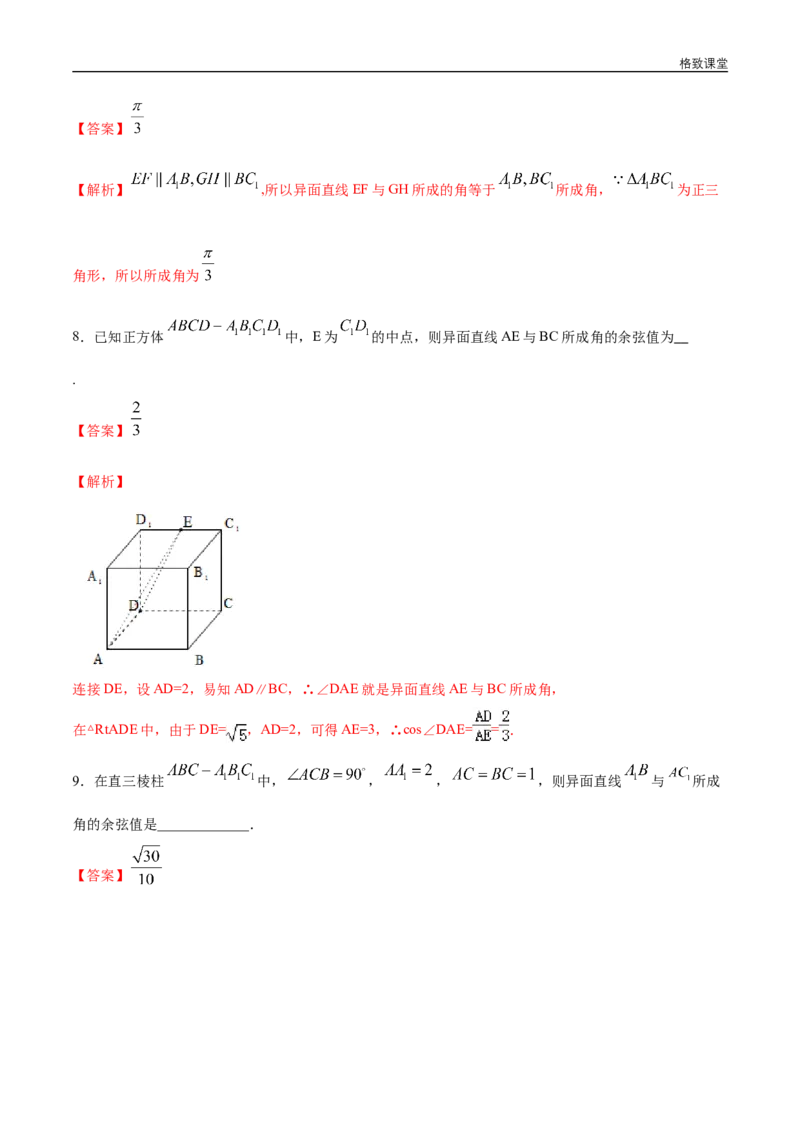
7.如图,在正方体ABCD﹣A B C D 中,E,F,G,H分别为AA ,AB,BB ,B C 的中点,则异面直线
1 1 1 1 1 1 1 1
EF与GH所成的角等于 .格致课堂
【答案】
【解析】 ,所以异面直线EF与GH所成的角等于 所成角, 为正三
角形,所以所成角为
8.已知正方体 中,E为 的中点,则异面直线AE与BC所成角的余弦值为
.
【答案】
【解析】
连接DE,设AD=2,易知AD∥BC,∴∠DAE就是异面直线AE与BC所成角,
在△RtADE中,由于DE= ,AD=2,可得AE=3,∴cos∠DAE= = .
9.在直三棱柱 中, , , ,则异面直线 与 所成
角的余弦值是_____________.
【答案】格致课堂
【解析】
连接 交 于点 ,取 中点 ,连接 ,则 ,连接
为异面直线 与 所成角
在 中, ,
,
同理可得 ,
,
异面直线 与 所成角的余弦值是
故答案为
10.在正方体 中,E、F、G、H分别为AA 、AB、BB 、B C 的中点,则所在直线与直
1 1 1 1
线EF是异面直线的是 ,异面直线EF与GH所成的角等于_____.格致课堂
CC ,DD ,C D ,A D ,B C
【答案】BC,CD,AD, 1 1 1 1 1 1 1 1, 60°
【解析】连接 , , ,由于EF∥AB,GH∥BC ,所以AB与BC 所成的角即为EF与GH所
1 1 1 1
成的角,由于△ABC 为正三角形,所以AB与BC 所成的角为60°,即EF与GH所成的角为60°.
1 1 1 1
三、解答题
11.空间四边形 中, , 分别是 的中点, ,求异面直线
所成的角.
【答案】
【解析】设G为AC的中点, 、F分别是AB、CD中点
且
且
为异面直线AD、BC所成的角(或其补角)格致课堂
,
中,
,
即异面直线AD、BC所成的角为
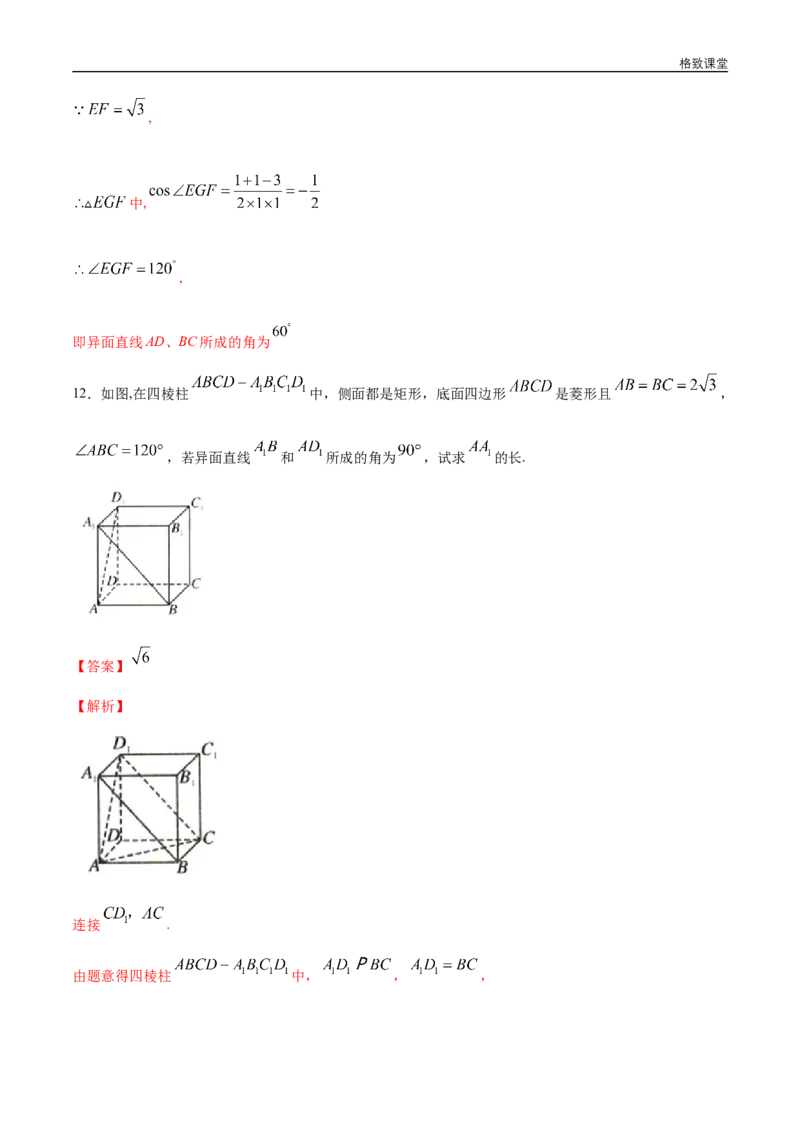
12.如图,在四棱柱 中,侧面都是矩形,底面四边形 是菱形且 ,
,若异面直线 和 所成的角为 ,试求 的长.
【答案】
【解析】
连接 .
由题意得四棱柱 中, , ,格致课堂
∴四边形 是平行四边形,
,
(或其补角)为 和 所成的角.
∵异面直线 和 所成的角为 ,
.
∵四棱柱 中, ,
是等腰直角三角形, .
∵底面四边形 是菱形且 , , ,
, .