文档内容
格致课堂
9.2.3 总体集中趋势的估计
(用时45分钟)
基础巩固
1.一组数据 , , , , , 的众数是 ,则这组数据的中位数是( )
A. B. C. D.
2.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与
实际平均数的差是 ( )
A.3.5 B.3 C.-0.5 D.-3
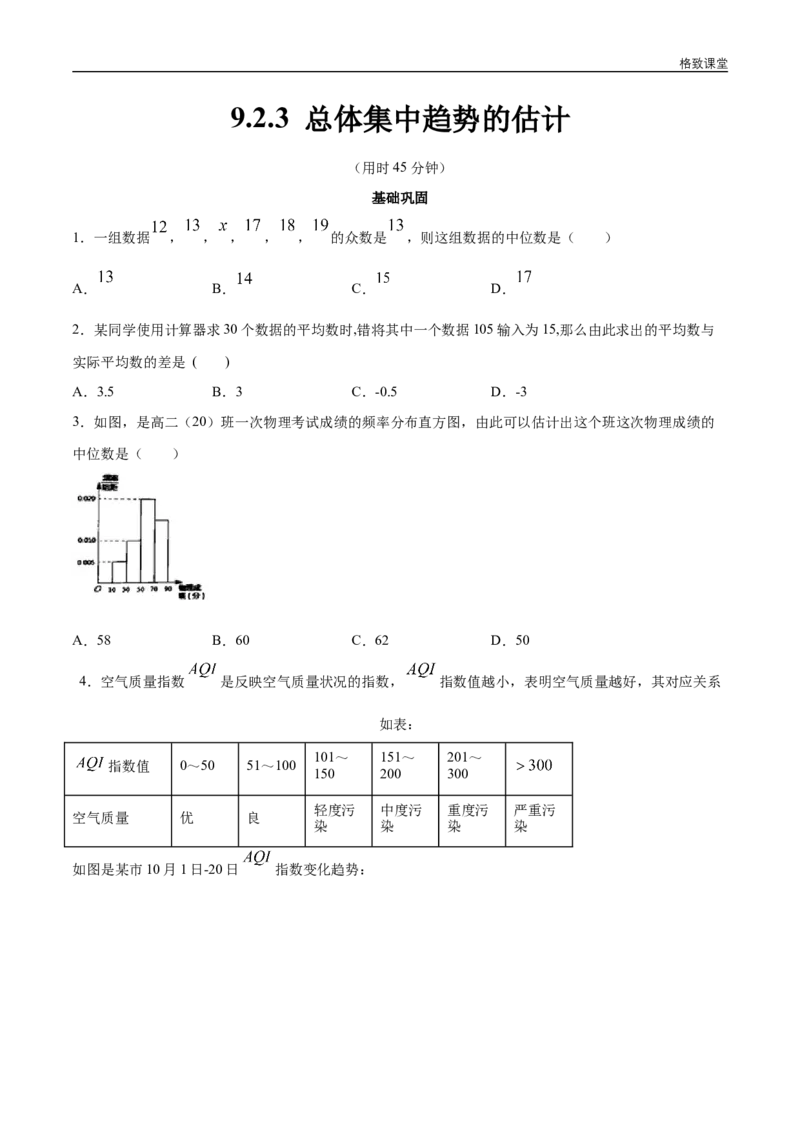
3.如图,是高二(20)班一次物理考试成绩的频率分布直方图,由此可以估计出这个班这次物理成绩的
中位数是( )
A.58 B.60 C.62 D.50
4.空气质量指数 是反映空气质量状况的指数, 指数值越小,表明空气质量越好,其对应关系
如表:
101~ 151~ 201~
指数值 0~50 51~100
150 200 300
轻度污 中度污 重度污 严重污
空气质量 优 良
染 染 染 染
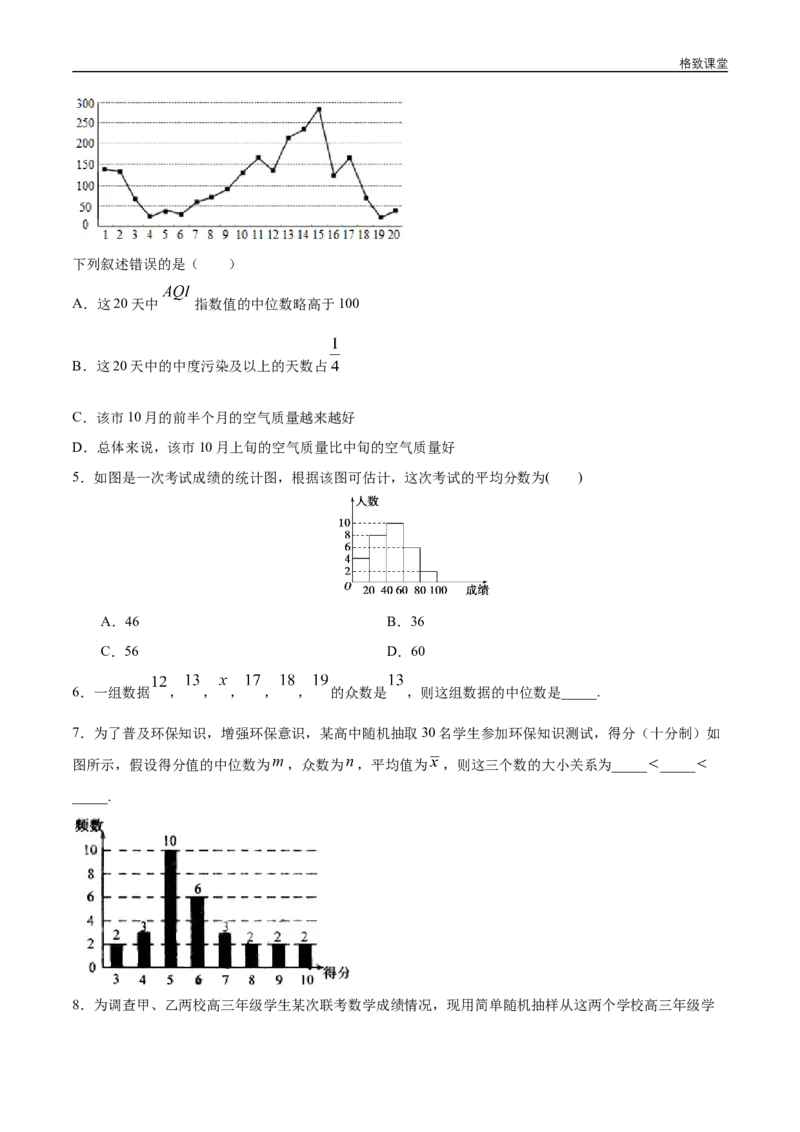
如图是某市10月1日-20日 指数变化趋势:格致课堂
下列叙述错误的是( )
A.这20天中 指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占
C.该市10月的前半个月的空气质量越来越好
D.总体来说,该市10月上旬的空气质量比中旬的空气质量好
5.如图是一次考试成绩的统计图,根据该图可估计,这次考试的平均分数为( )
A.46 B.36
C.56 D.60
6.一组数据 , , , , , 的众数是 ,则这组数据的中位数是_____.
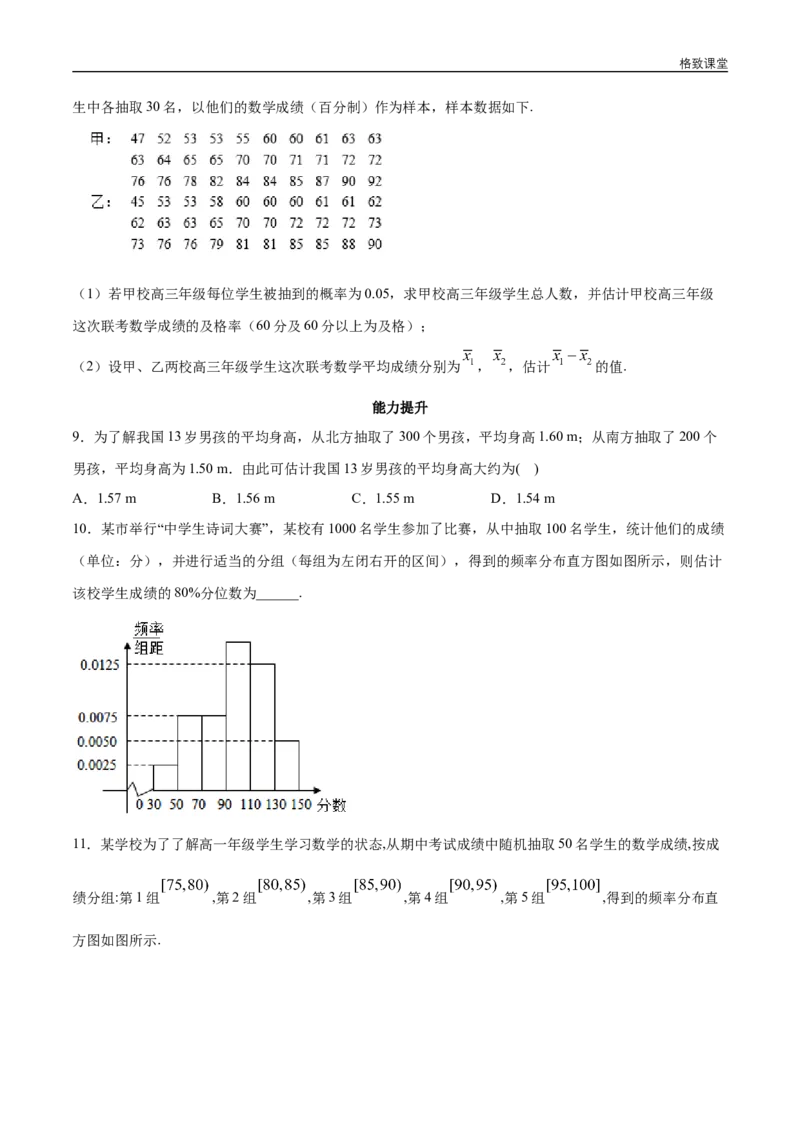
7.为了普及环保知识,增强环保意识,某高中随机抽取30名学生参加环保知识测试,得分(十分制)如
图所示,假设得分值的中位数为 ,众数为 ,平均值为 ,则这三个数的大小关系为_____ _____
_____.
8.为调查甲、乙两校高三年级学生某次联考数学成绩情况,现用简单随机抽样从这两个学校高三年级学格致课堂
生中各抽取30名,以他们的数学成绩(百分制)作为样本,样本数据如下.
(1)若甲校高三年级每位学生被抽到的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级
这次联考数学成绩的及格率(60分及60分以上为及格);
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为 , ,估计 的值.
能力提升
9.为了解我国13岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60 m;从南方抽取了200个
男孩,平均身高为1.50 m.由此可估计我国13岁男孩的平均身高大约为( )
A.1.57 m B.1.56 m C.1.55 m D.1.54 m
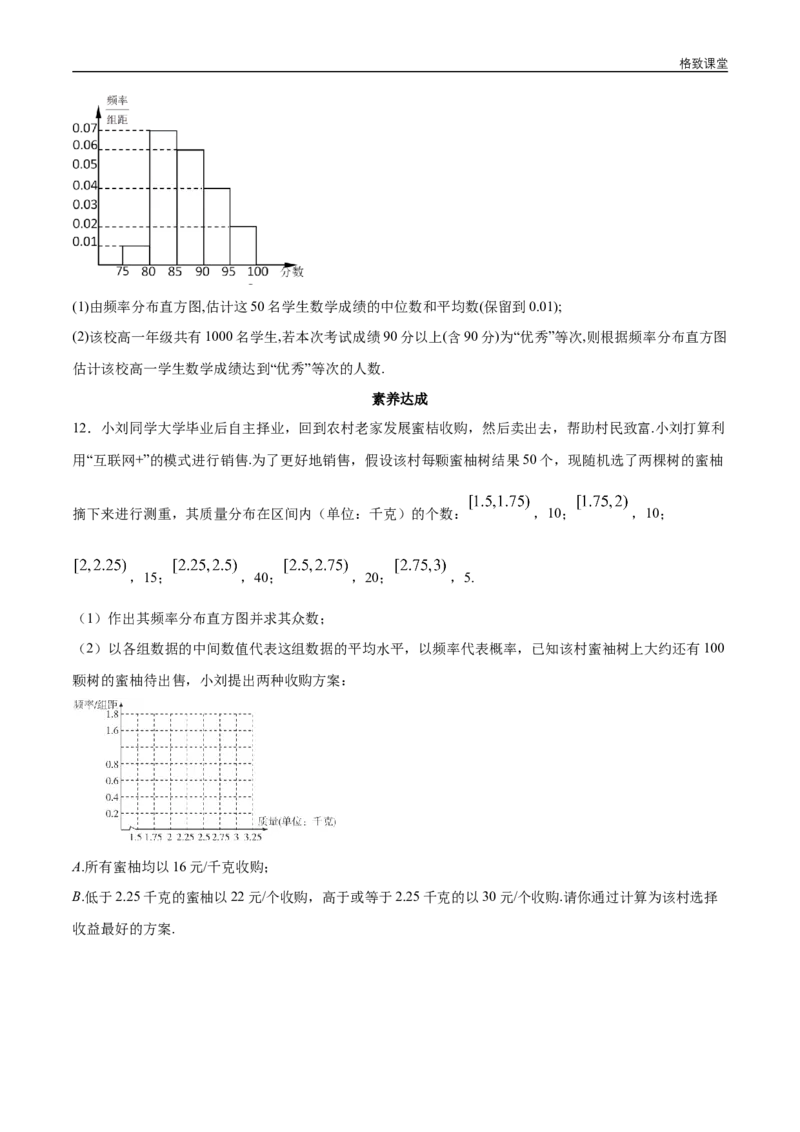
10.某市举行“中学生诗词大赛”,某校有1000名学生参加了比赛,从中抽取100名学生,统计他们的成绩
(单位:分),并进行适当的分组(每组为左闭右开的区间),得到的频率分布直方图如图所示,则估计
该校学生成绩的80%分位数为______.
11.某学校为了了解高一年级学生学习数学的状态,从期中考试成绩中随机抽取50名学生的数学成绩,按成
绩分组:第1组 ,第2组 ,第3组 ,第4组 ,第5组 ,得到的频率分布直
方图如图所示.格致课堂
(1)由频率分布直方图,估计这50名学生数学成绩的中位数和平均数(保留到0.01);
(2)该校高一年级共有1000名学生,若本次考试成绩90分以上(含90分)为“优秀”等次,则根据频率分布直方图
估计该校高一学生数学成绩达到“优秀”等次的人数.
素养达成
12.小刘同学大学毕业后自主择业,回到农村老家发展蜜桔收购,然后卖出去,帮助村民致富.小刘打算利
用“互联网+”的模式进行销售.为了更好地销售,假设该村每颗蜜柚树结果50个,现随机选了两棵树的蜜柚
摘下来进行测重,其质量分布在区间内(单位:千克)的个数: ,10; ,10;
,15; ,40; ,20; ,5.
(1)作出其频率分布直方图并求其众数;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村蜜袖树上大约还有100
颗树的蜜柚待出售,小刘提出两种收购方案:
A.所有蜜柚均以16元/千克收购;
B.低于2.25千克的蜜柚以22元/个收购,高于或等于2.25千克的以30元/个收购.请你通过计算为该村选择
收益最好的方案.