文档内容
格致课堂
9.2.2 总体百分数的估计
(用时45分钟)
【选题明细表】
知识点、方法 题号
总体百分数的理解 1
由数据计算第P百分数 2,4,7,9
由频率分布直方图(表)计算第P百分数 3,5,6,8,10
综合应用 11,12
基础巩固
1.对于考试成绩的统计,如果你的成绩处在第95的百分位数上,以下说法正确的是( )
A.你得了95分
B.你答对了95%的试题
C.95%的参加考试者得到了和你一样的考分或还要低的分数
D.你排名在第95名
【答案】C
【解析】第95的百分位数是指把数据从小到大排序,有至少95%数据小于或等于这个数,至少有5%的数
据大于或等于这个值,故选C.
2.某校调查某班30名同学所穿的鞋的尺码如下表所示:
码号 33 34 35 36 37
人数 7 6 14 1 2
则这组数据的25%分位数是( )
A.33 B.34 C.35 D.36
【答案】B
【解析】因为30×25%=7.5,所以这组数据的25%分位数为34.故选B.
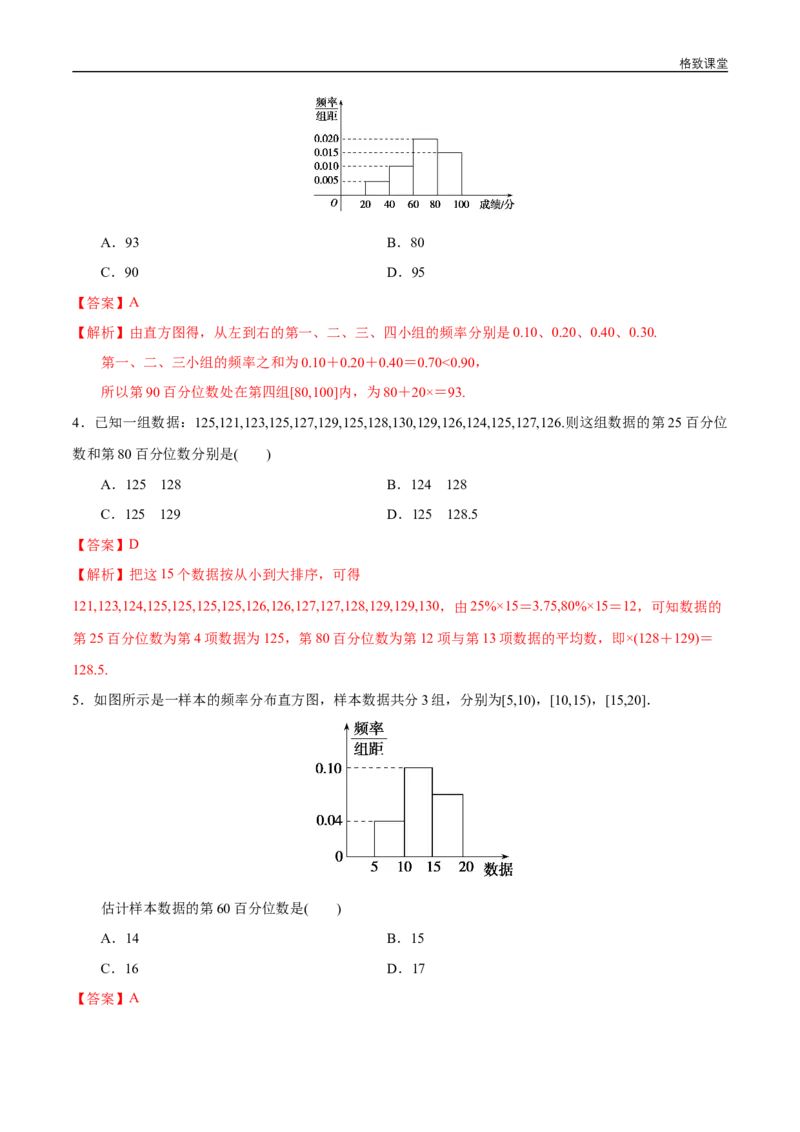
3.某班的全体学生参加消防安全知识竞赛,成绩的频率分布直方图如图,数据的分组依次为:[20,40),
[40,60),[60,80),[80,100].估计本班学生的消防安全知识成绩的第90百分位数是( )格致课堂
A.93 B.80
C.90 D.95
【答案】A
【解析】由直方图得,从左到右的第一、二、三、四小组的频率分别是0.10、0.20、0.40、0.30.
第一、二、三小组的频率之和为0.10+0.20+0.40=0.70<0.90,
所以第90百分位数处在第四组[80,100]内,为80+20×=93.
4.已知一组数据:125,121,123,125,127,129,125,128,130,129,126,124,125,127,126.则这组数据的第25百分位
数和第80百分位数分别是( )
A.125 128 B.124 128
C.125 129 D.125 128.5
【答案】D
【解析】把这15个数据按从小到大排序,可得
121,123,124,125,125,125,125,126,126,127,127,128,129,129,130,由25%×15=3.75,80%×15=12,可知数据的
第25百分位数为第4项数据为125,第80百分位数为第12项与第13项数据的平均数,即×(128+129)=
128.5.
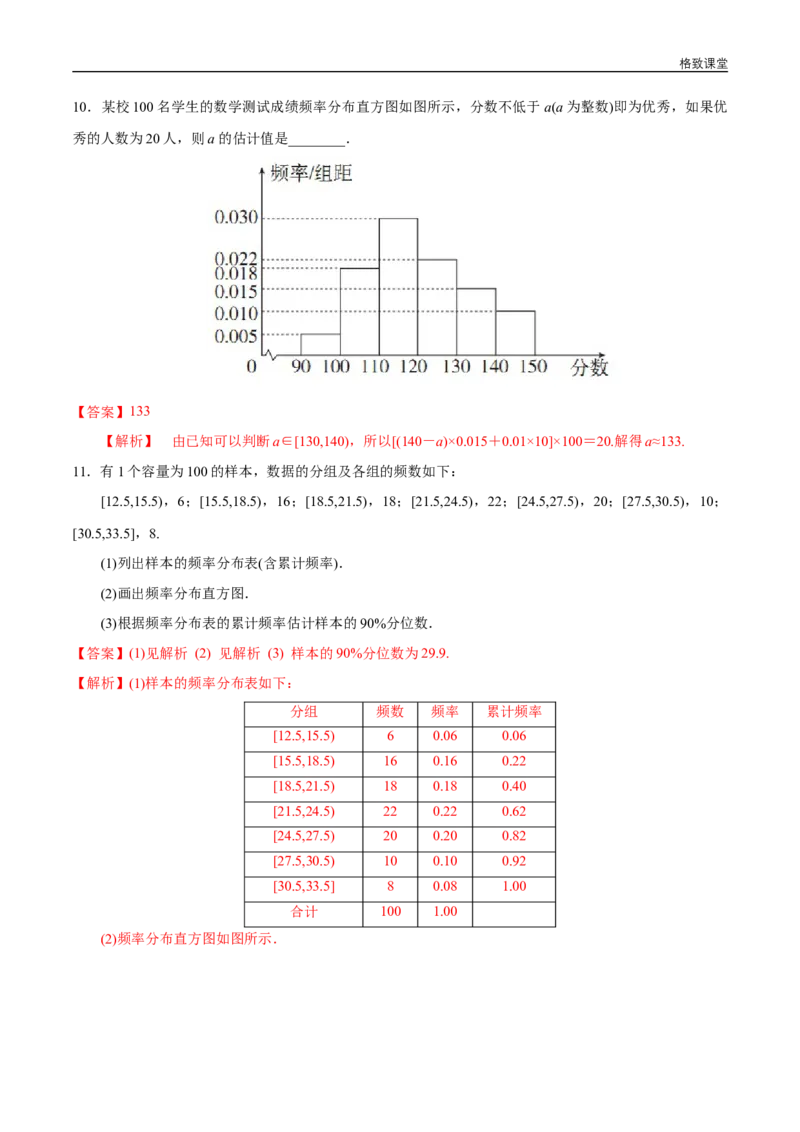
5.如图所示是一样本的频率分布直方图,样本数据共分3组,分别为[5,10),[10,15),[15,20].
估计样本数据的第60百分位数是( )
A.14 B.15
C.16 D.17
【答案】A格致课堂
【解析】第1组[5,10)的频率为0.04×(10-5)=0.20;
第2组[10,15)的频率为0.10×5=0.50;
所以第60百分位数是10+5×=14.
6.从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及
频数分布表.
组合 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
估计本校学生的一周课外阅读时间的第90百分位数________.
【答案】12
【解析】因为前6组的频率之和为0.90,所以第90百分位数为12.据此可以估计本校学生的一周课外阅读
时间的第90百分位数约为12.
7 . 从 某 城 市 随 机 抽 取 14 台 自 动 售 货 机 , 对 其 销 售 额 进 行 统 计 , 数 据 如 下 :
8,8,10,12,22,23,20,23,32,34,31,34,42,43.则这14台自动售货机的销售额的第50百分位数分别为________.
【答案】23
【解析】把14台自动售货机的销售额按从小到大排序,得8,8,10,12,20,22,23,23,31,32,34,34,42,43.因为
14×50%=7,14×80%=11.2,所以第50百分位数是第7项和第8项数据的平均数,即×(23+23)=23.
8.山东省教育厅为了了解和掌握2019年高考考生的实际答卷情况,随机地取出了100名考生的数学成绩
(单位:分),将数据分成了11组,制成了如图所示的频率分布表:
分组 频数 频率
[80,85) 1 0.01
[85,90) 2 0.02
[90,95) 4 0.04
[95,100) 14 0.14
[100,105) 24 0.24格致课堂
[105,110) 15 0.15
[110,115) 12 0.12
[115,120) 9 0.09
[120,125) 11 0.11
[125,130) 6 0.06
[130,135] 2 0.02
合计 100 1
(1)求样本数据的第60,80百分位数.
(2)估计2019年高考考生的数学成绩的90%分位数.
【答案】(1)第60百分位数为110,第80百分位数约为119.4.
(2)数学成绩的90%分位数为124.1.
【解析】从频率分布表得,前六组的频率之和为0.01+0.02+0.04+0.14+0.24+0.15=0.60,
前七组的频率之和为0.60+0.12=0.72,
前八组的频率之和为0.72+0.09=0.81,
前九组的频率之和为0.81+0.11=0.92.
(1)由前六组的频率之和为0.60,得样本数据的第60百分位数为110,样本数据的第80百分位数一定
在第八组[115,120)内,由115+5×=119.4,估计样本数据的第80百分位数约为119.4.
(2)由前八组的频率之和为0.81,前九组的频率之和为0.92,知90%分位数一定在第九组[120,125)内,
由120+5×=124.1,估计2019年高考考生的数学成绩的90%分位数为124.1.
能力提升
9.从某校高一新生中随机抽取一个容量为20的身高样本,数据从小到大排序如下(单位:cm),
152,155,158, 164, 164, 165, 165, 165, 166, 167, 168, 168, 169, 170, 170, 170, 171,x, 174, 175.若样本数据
的第90百分位数是173,则x的值为( )
A.171 B.172
C.173 D.174
【答案】B
【解析】因为20×90%=18,所以第90百分位数是第18项和第19项数据的平均数,即(x+174)=173,所
以x=172.格致课堂
10.某校100名学生的数学测试成绩频率分布直方图如图所示,分数不低于a(a为整数)即为优秀,如果优
秀的人数为20人,则a的估计值是________.
【答案】133
【解析】 由已知可以判断a∈[130,140),所以[(140-a)×0.015+0.01×10]×100=20.解得a≈133.
11.有1个容量为100的样本,数据的分组及各组的频数如下:
[12.5,15.5),6;[15.5,18.5),16;[18.5,21.5),18;[21.5,24.5),22;[24.5,27.5),20;[27.5,30.5),10;
[30.5,33.5],8.
(1)列出样本的频率分布表(含累计频率).
(2)画出频率分布直方图.
(3)根据频率分布表的累计频率估计样本的90%分位数.
【答案】(1)见解析 (2) 见解析 (3) 样本的90%分位数为29.9.
【解析】(1)样本的频率分布表如下:
分组 频数 频率 累计频率
[12.5,15.5) 6 0.06 0.06
[15.5,18.5) 16 0.16 0.22
[18.5,21.5) 18 0.18 0.40
[21.5,24.5) 22 0.22 0.62
[24.5,27.5) 20 0.20 0.82
[27.5,30.5) 10 0.10 0.92
[30.5,33.5] 8 0.08 1.00
合计 100 1.00
(2)频率分布直方图如图所示.格致课堂
(3)由频率分布表的累计频率知,小于 30.5的数据所占的比例为92%,所以90%分位数一定在区间
[27.5,30.5)内,由27.5+3×=29.9,可以估计样本的90%分位数为29.9.
素养达成
12. 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电
量不超过200千瓦时的部分按0.5元/千瓦时收费,超过200千瓦时但不超过400千瓦时的部分按0.8元/千
瓦时收费,超过400千瓦时的部分按1.0元/千瓦时收费.
(1)求某户居民用电费用y(单位:元)关于月用电量x(单位:千瓦时)的函数解析式.
(2)为了了解居民的用电情况,通过抽样获得了今年1月份100户居民每户的用电量,统计分析后得到
如图所示的频率分布直方图.若这100户居民中,今年1月份用电费用不超过260元的占80%,求a,b的
值.
(3)根据(2)中求得的数据计算用电量的75%分位数.
【答案】(1) y=(2) a=0.001 5,b=0.002 0.
(3) 用电量的75%分位数为375千瓦时..
【解析】 (1)当0≤x≤200时,y=0.5x;
当200400时,y=0.5×200+0.8×200+1.0×(x-400)=x-140.
所以y与x之间的函数解析式为
y=
(2)由(1)可知,当y=260时,x=400,即用电量不超过400千瓦时的占80%,
结合频率分布直方图可知
解得a=0.001 5,b=0.002 0.格致课堂
(3)设75%分位数为m,
因为用电量低于300千瓦时的所占比例为(0.001+0.002+0.003)×100=60%,
用电量不超过400千瓦时的占80%,
所以75%分位数为m在[300,400)内,所以0.6+(m-300)×0.002=0.75,
解得m=375千瓦时,即用电量的75%分位数为375千瓦时.