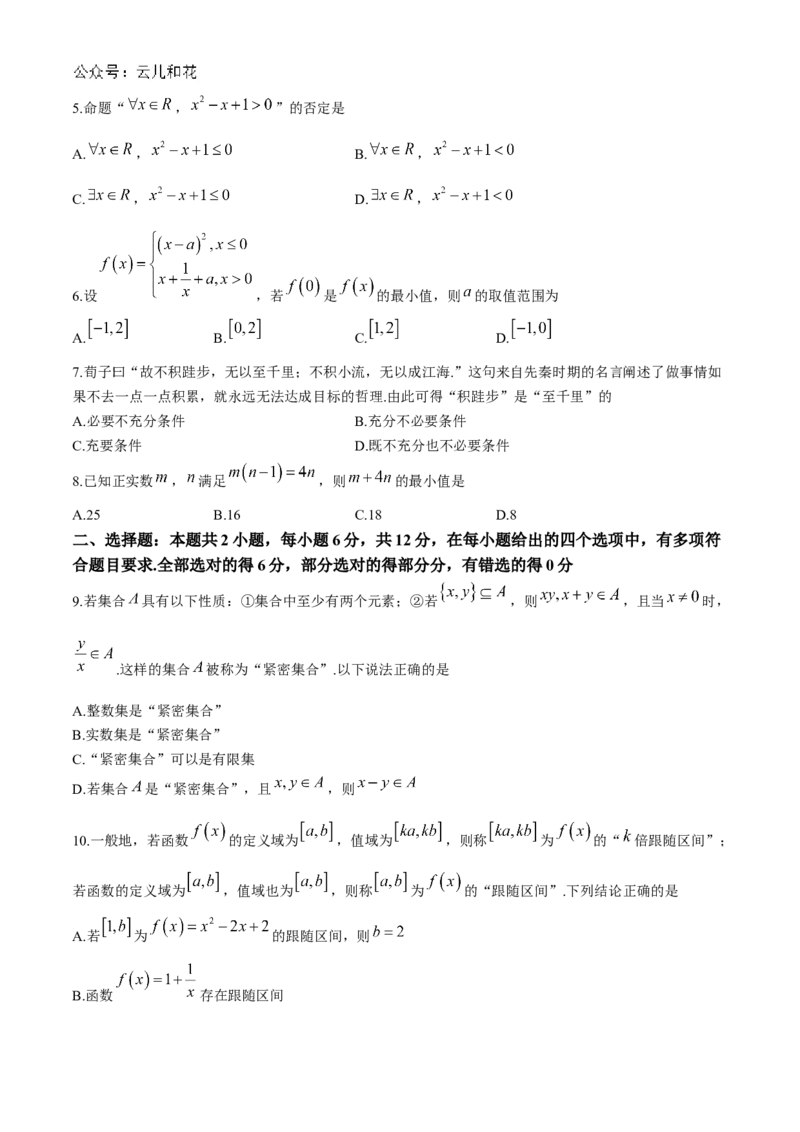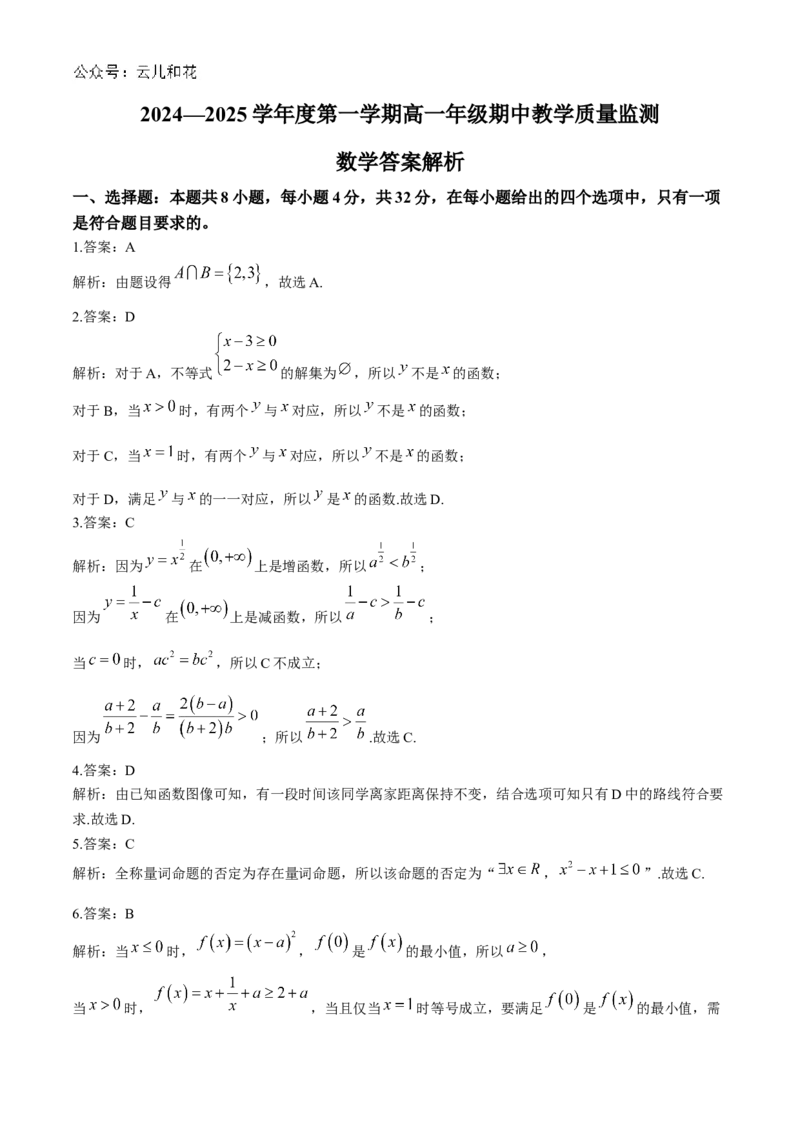文档内容
大同市 2024—2025 学年度第一学期期中高一年级教学质量监测
数学
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上相应的位置.
2.全部答案在答题卡上完成,答在本试卷上无效.
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案用0.5mm黑色笔迹签字
笔写在答题卡上.
4.考试结束后,将本试卷和答题卡一并交回.
5.本试卷共4页,满分100分,考试时间90分钟
一、选择题:本题共8小题,每小题4分,共32分,在每小题给出的四个选项中,只有一项
是符合题目要求的
1.设集合 , ,则
A. B. C. D.
2.下列关于 , 的关系中, 是 的函数的是
A. B.
1 2 3 4
0 0 -6 1
C. D.
3.设 , ,则下列不等式中不正确的是
A. B. C. D.
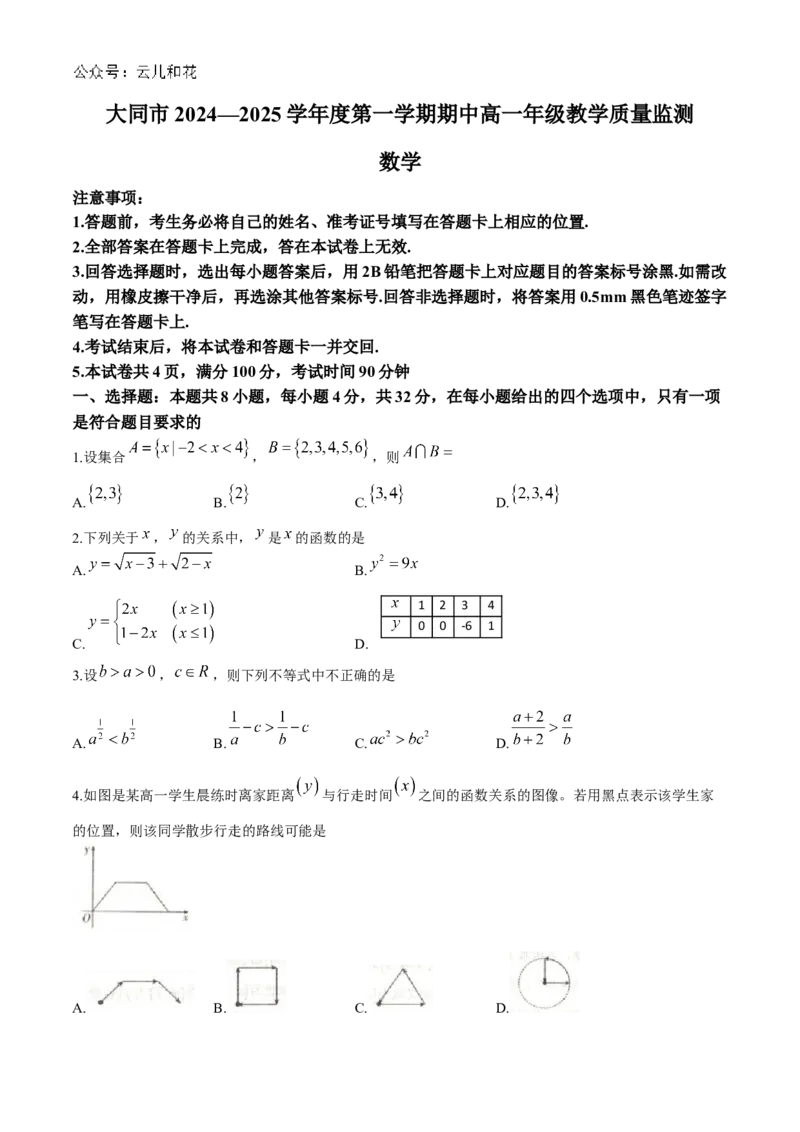
4.如图是某高一学生晨练时离家距离 与行走时间 之间的函数关系的图像。若用黑点表示该学生家
的位置,则该同学散步行走的路线可能是
A. B. C. D.5.命题“ , ”的否定是
A. , B. ,
C. , D. ,
6.设 ,若 是 的最小值,则 的取值范围为
A. B. C. D.
7.荀子曰“故不积跬步,无以至千里;不积小流,无以成江海.”这句来自先秦时期的名言阐述了做事情如
果不去一点一点积累,就永远无法达成目标的哲理.由此可得“积跬步”是“至千里”的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
8.已知正实数 , 满足 ,则 的最小值是
A.25 B.16 C.18 D.8
二、选择题:本题共2小题,每小题6分,共12分,在每小题给出的四个选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有错选的得0分
9.若集合 具有以下性质:①集合中至少有两个元素;②若 ,则 ,且当 时,
.这样的集合 被称为“紧密集合”.以下说法正确的是
A.整数集是“紧密集合”
B.实数集是“紧密集合”
C.“紧密集合”可以是有限集
D.若集合 是“紧密集合”,且 ,则
10.一般地,若函数 的定义域为 ,值域为 ,则称 为 的“ 倍跟随区间”;
若函数的定义域为 ,值域也为 ,则称 为 的“跟随区间”.下列结论正确的是
A.若 为 的跟随区间,则
B.函数 存在跟随区间C.若函数 存在跟随区间,则
D.二次函数 存在“3倍跟随区间”
三、填空题:本题共2小题,每小题4分,共8分.
11.已知二次函数 的图像过原点,且 , ,则 的取值范围是
________.
12.已知 为 上的奇函数, ,若对任意 ,当 时,都有
,则不等式 的解集为________.
四、解答题:本题共5小题,共48分.解答应写出文字说明、证明过程或演算步骤.
13.(8分)
(1)已知 , ,求 的值:
(2)已知 ,求 的值.
14.(8分)
已知函数 ,且 .
(1)求 的值;
(2)若 ,求实数 的取值范围.
15.(8分)
设函数 , .
(1)当 时,求函数 的最大值和最小值:
(2)若函数的最小值为 ,求 .
16.(12分)
函数 的定义域为 ,且满足对于任意 ,有 .
(1)求 的值;(2)判断 的奇偶性并证明你的结论;
(3)如果 , ,且 在 上是增函数,求 的取值范围.
17.(12分)
某公司为调动员工工作极性拟制定以下奖励方案,要求奖金 (单位:万元随投资收益 (单位:万元)
的增加而增加,奖金不超过90万元,同时奖金不超过投资收益的 .即假定奖励方案模拟函数为
时,该公司对函数模型的基本要求是:当 时,① 是增函数; 恒
成立;③ 恒成立.
(1)现有两个奖励函数模型:(I) ;(II) .试分析这两个函数模型是
否符合公司要求?
(2)已知函数 符合公司奖励方案函数模型要求,求实数 的取值范围.2024—2025 学年度第一学期高一年级期中教学质量监测
数学答案解析
一、选择题:本题共8小题,每小题4分,共32分,在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.答案:A
解析:由题设得 ,故选A.
2.答案:D
解析:对于A,不等式 的解集为 ,所以 不是 的函数;
对于B,当 时,有两个 与 对应,所以 不是 的函数;
对于C,当 时,有两个 与 对应,所以 不是 的函数;
对于D,满足 与 的一一对应,所以 是 的函数.故选D.
3.答案:C
解析:因为 在 上是增函数,所以 ;
因为 在 上是减函数,所以 ;
当 时, ,所以C不成立;
因为 ;所以 .故选C.
4.答案:D
解析:由已知函数图像可知,有一段时间该同学离家距离保持不变,结合选项可知只有D中的路线符合要
求.故选D.
5.答案:C
解析:全称量词命题的否定为存在量词命题,所以该命题的否定为“ , ”.故选C.
6.答案:B
解析:当 时, , 是 的最小值,所以 ,
当 时, ,当且仅当 时等号成立,要满足 是 的最小值,需,即 ,解得 .
所以 的取值范围是 .故选B.
7.答案:A
解析:荀子的名言表明积跬步未必能至千里,但要至千里必须积跬步,故“积跬步”是“至千里”的必要
不充分条件.故选A.
8.答案:B
解析:由 得 ,又 ,因为 ,
,所以原式 ,当且仅当 ,即 , 时等号成立.故选B.
二、选择题:本题共2小题,每小题6分,共12分,在每小题给出的四个选项中,有多项符
合题目要求。全部选对的得6分,部分选对的得部分分,有错选的得0分。
9.答案:BC
解析:若 , ,而 ,故整数集不是“紧密集合”,A错误;
根据“紧密集合”的性质,知实数集是“紧密集合”,B正确;
集合 是“紧密集合”,故“紧密集合”可以是有限集,C正确;
集合 是“紧密集合”,当 , 时, ,D错误,
故选BC.
10.答案:ACD
解析:对于A,由已知可得函数 在区间 上单调递增,由 ,解得 或
(舍去),所以 ,A正确;
对于B,若存在跟随区间 ,因为函数在单调区间上单调递减,则由 解得
或 ,不满足 ,故不存在,B不正确;
对于C,由已知得,函数在定义域上单调递减,若存在跟随区间 ,则有 即两式作差得, ,即 ,又
,所以 ,易得 ,所以 ,
设 ,由于 ,所以 ,即 ,则 ,解
得 ,C正确;
对于D,若函数存在3倍跟随区间,设定义域为 ,值域为 ,当 时,易得函数在定义
域上单调递增,则 , 是方程 的两个不相等的实数根,解得 或 ,故存在定
义域为 使得值域为 ,D正确.故选ACD.
三、填空题:本题共2小题,每小题4分,共8分。
11.答案:
解析:设 ,
由 ,得
所以 ,又 ,所以 ,
即 的取值范围是 .
12.答案:
解析:令 ,又 为 上的奇函数,
所以 为 上的偶函数,且 ,又对任意 ,当 时,都有 ,
即相当于 ,
所以 在 上单调递减,
又 ,所以 ,
所以不等式 ,
即 ,所以 ,即 ,
又 ,所以 中,要满足 成立,
还需 ,即
所以 .
四、解答题:本题共5小题,共48分。解答应写出文字说明、证明过程或演算步骤。
13.(8分)
解析:
(1)
……(4分)
(2)因为 ,所以 ,
又 ,所以 .……(8分)
14.(8分)
解析:
(1)因为 ,所以 ,即 ,所以 ……(2分)
(2)由于 ,所以其定义域为 ,……(3分)又 在 上是增函数.……(4分)
由 可得 ,解得 ,……(7分)
所以实数 的取值范围为 .……(8分)
15.(8分)
解析:
(1)当 时,函数 , ,所以函数 的最大值为 ,最小
值为 .……(2分)
(2) 的对称轴为直线 ;
①当 ,即 时,此时 在 上单调递增,所以当 时函数取得最小值
;……(4分)
②当 ,即 时,此时 在 上单调递减,所以当 时函数取得最小值
;……(6分)
③当 ,即 时,此时 在 上先减后增,所以函数在 时取得最小值,
即 .……(8分)
16.(12分)
解析:
(1)因为对于任意 ,都有 ,所以令 ,得 ,
所以 .……(2分)(2) 为偶函数.……(3分)
证明如下: 的定义域关于原点对称,
令 ,有 ,所以 .
令 , ,有 ,
所以 ,所以 为偶函数.……(7分)
(3)依题设有 ,由(2)知 是偶函数,
所以 等价于 ,……(9分)
又 在 上是增函数,
所以 ,
解得 且 ,
所以 的取值范围是 .……(12分)
17.(12分)
解析:
(1)对于函数模型:(I) ,
用验证条件③时,当 时, ,而 ,
即 不恒成立,故不符合公司要求;……(2分)
对于函数模型:(II) ,
当 时,条件① 是增函数满足,
所以 ,满足条件②;对于条件③,记 ,
则 ,
因为 ,所以当 时,
,
所以 恒成立,即条件③也成立.
故函数模型(Ⅱ) 符合公司要求.……(6分)
(2)因为 ,所以函数 符合条件①,
由函数 符合条件②,
得 ,解得 ;……(8分)
由函数 符合条件③,
得 对 恒成立,……(9分)
即 对 恒成立.
因为 ,当且仅当 ,
即 时等号成立,所以 ,……(11分)
综上所述,实数 的取值范围是 .……(12分)