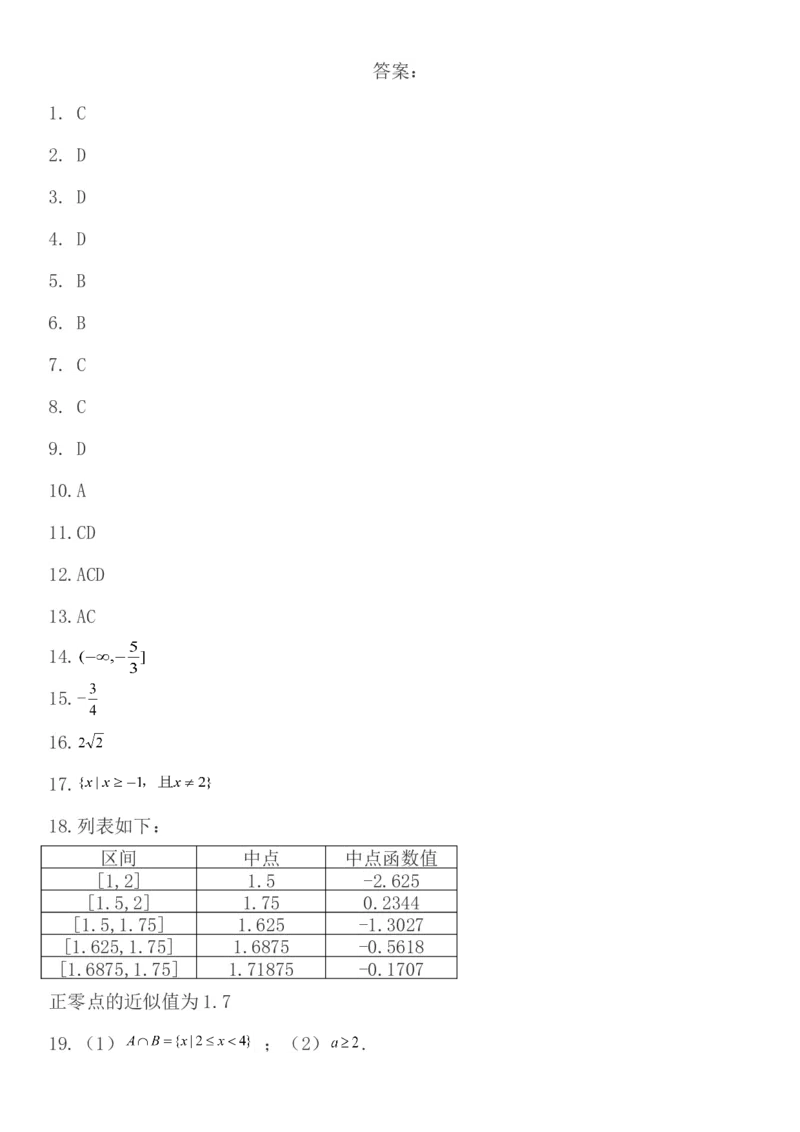文档内容
2022-2023 年度
新教材必修第一册:期末综合测试卷(二)
一、单项选择题:本题 10 小题,每小题 4 分,共 52 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.设集合 ,则 ( )
A.∅ B. C. D.
2.已知函数 的定义域为 ,则函数 定义域为( )
A. B. C. D.
3.不等式 的解集为( )
A. B. C. D.
4.设 ,则 的大小关系是( )
A. B. C. D.
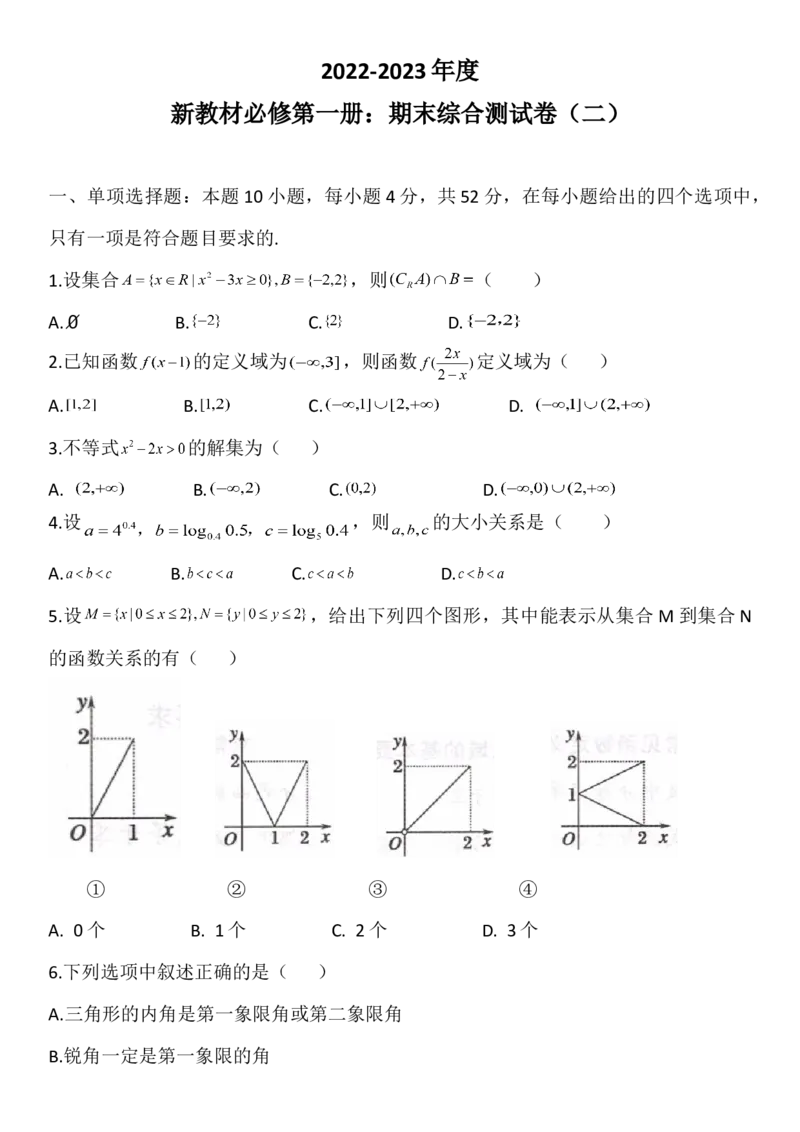
5.设 ,给出下列四个图形,其中能表示从集合 M 到集合 N
的函数关系的有( )
① ② ③ ④
A. 0个 B. 1个 C. 2个 D. 3个
6.下列选项中叙述正确的是( )
A.三角形的内角是第一象限角或第二象限角
B.锐角一定是第一象限的角C.小于90°的角一定是锐角
D.终边相同的角一定相等
7.若点P ,则P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.下列结论错误的是( )
A.命题“若 ,则 ”为真命题.
B.“ ”是“ ”的充分不必要条件
C.已知命题 “若 ,则方程 有实数根”,则命题 的否定为真命题
D.命题“若 ,则 且 ”的为真命题
9.已知函数 有两个零点 ,则有( )
A. B. C. D.
10.函数 ,其单调性是( ).
A.在 上是增函数,在 上是减函数
B.在 上是增函数,在 和 上都是减函数
C.在 上是增函数,在 上是减函数
D.在 和 上都是增函数,在 上是减函数
二、多项选择题(本大题共 3 小题,每小题 4 分,共 12 分.在每小题给出的四个选项
中,有多项符合题目要求.全部选对的得 4 分,选对但不全的得 2 分,有选错的得 0
分)
11.设 ,若 ,则下列不等式中正确的是( )
A. B.
C. D.
12.函数 的图像与直线 有且只有两个不同的
交点,则 的取值不可能是( )A.1 B.2 C. 3 D.-1
13.已知 ,角 的终边经过点 ,则下列结论正确的是( )
A. B. C. D.
三、填空题:本题共4小题,每小题4分,共16分.
14.已知函数 的一个零点为0,则 的单调递增区间为 ;
15.已知 为第四象限角, ,则 的值为 .
16.当 且 时,函数 的图像恒过点A,若点A在直线 上,
则 的最小值为 .
17.函数 的定义域为 .
三、解答题:本题共6分,共82分.解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分12分)
用二分法求函数 的一个正零点(精确到0.1).
19.(本题满分14分)
设全集U=R,集合 ,
(1)求 ;
(2)若 ,求实数 的取值范围.
20.(本小题满分14分)
已知
求证: 在 上是减函数.21.(本小题满分14分)
某摩托车生产企业,上年度生产摩托车的投入成本为 1 万元/辆,出厂价为 1.2 万
元/辆,年销售量为 10000 辆,本年度为适应市场需求,计划适度增加投入成本,提
高产品的档次.若每辆车投入成本增加的比例为 ,则出厂价相应的提高比例
为 ,同时预计年销售量增加的比例为
(1)写出本年度预计的年利润 与投入成本增加的比例 的关系式;
(2)投入成本增加的比例多大时,本年度预计的年利润最大?最大值是多少?
22.(本小题满分14分)
已知
(1)化简
(2)若 ,求 的值.23.(本小题满分14分)
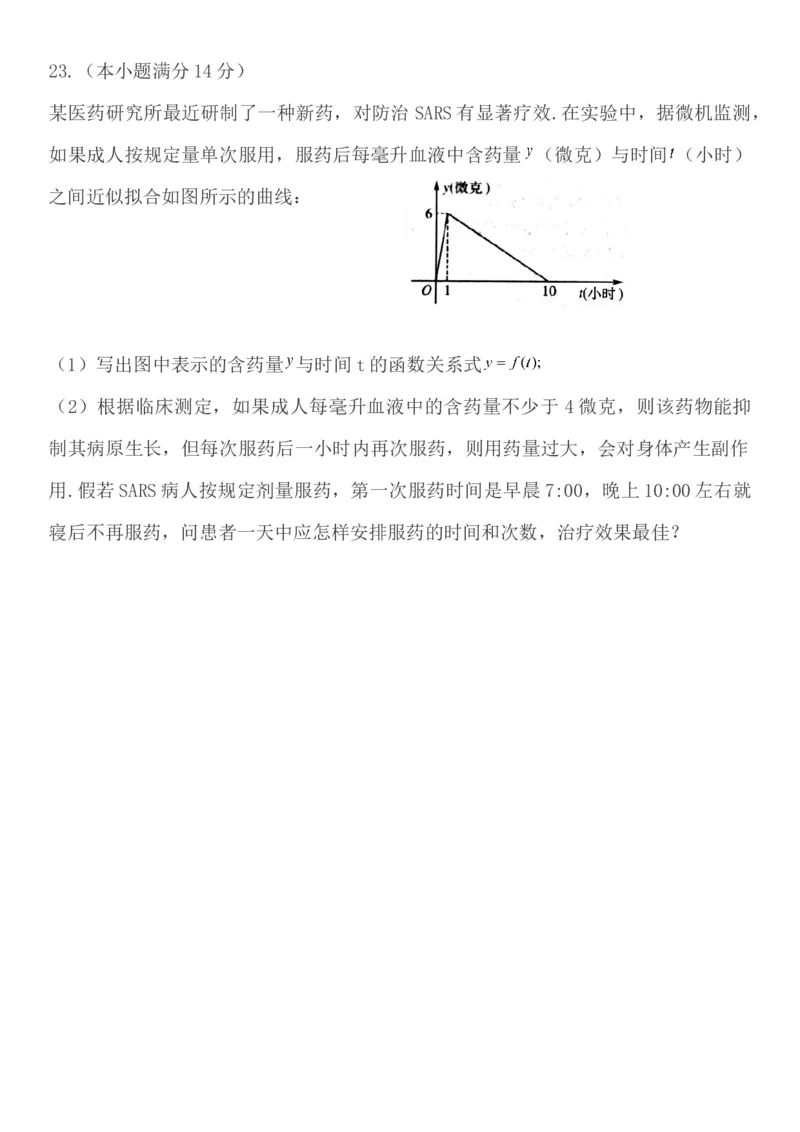
某医药研究所最近研制了一种新药,对防治 SARS有显著疗效.在实验中,据微机监测,
如果成人按规定量单次服用,服药后每毫升血液中含药量 (微克)与时间 (小时)
之间近似拟合如图所示的曲线:
(1)写出图中表示的含药量 与时间t的函数关系式
(2)根据临床测定,如果成人每毫升血液中的含药量不少于 4 微克,则该药物能抑
制其病原生长,但每次服药后一小时内再次服药,则用药量过大,会对身体产生副作
用.假若SARS病人按规定剂量服药,第一次服药时间是早晨 7:00,晚上10:00左右就
寝后不再服药,问患者一天中应怎样安排服药的时间和次数,治疗效果最佳?答案:
1. C
2. D
3. D
4. D
5. B
6. B
7. C
8. C
9. D
10.A
11.CD
12.ACD
13.AC
14.
15.-
16.
17.
18.列表如下:
区间 中点 中点函数值
[1,2] 1.5 -2.625
[1.5,2] 1.75 0.2344
[1.5,1.75] 1.625 -1.3027
[1.625,1.75] 1.6875 -0.5618
[1.6875,1.75] 1.71875 -0.1707
正零点的近似值为1.7
19.(1) ;(2) .20.证明:任取 ,且 令 ,则
即
综上, 在 上是减函数.
21.(1) =
(2)函数 的图像开口向下,对称轴为直线 .
∴当 时, 取得最大值 .
∴投入成本增加的比例为 时,本年度预计的年利润最大,最大值是 万元.
22.(1)原式等于=
(2)∵ ,∴
23.(1)
(2)考虑到晚上 10:00 左右就寝后不再服药,故一天中安排四次服药为宜,服药时
间分别为早晨7:00,上午11:00,下午16:00和晚上20:30.