文档内容
2025~2026 学年第一学期期中七校联合调研试题高一数学
2025.11
注意事项:
1.本试卷考试时间为 120 分钟,试卷满分 150分,考试形式闭卷.
2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
3.答题前,务必将自己的姓名、准考证号用 0.5毫米黑色墨水签字笔填写在试卷及答题卡上.
一、选择题:本大题共 8 小题,每小题 5分,共 40 分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.命题“x∈R,x2-x+1≤0”的否定为
A.x∈R,x2-x+1>0 B.x∈R,x2-x+1>0
C.xR,x2-x+1>0 D.xR,x2-x+1≤0
1
2.设集合M={x|x2-4<0},N={x| ≤x≤5},则M∩N等于
3
1 1
A.{x|0<x≤ } B.{x| ≤x<2}
3 3
C.{x|4≤x<5} D.{x|-2<x≤5}
4-x
3.函数f(x)= 的定义域为
x-1
A.(-∞,4) B.(1,4)∪(4,+∞)
C.[4,+∞) D.(-∞,1)∪(1,4]
4.命题“k>4”是命题“x2-4x+k2-3k>0对一切实数x恒成立”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
x2-2ax+6,x≤1
5.已知函数f(x)= a 是R上的减函数,则实数a的取值范围是
x
,x>1
7
A.[1, ) B.[1,+∞)
3
7
C.[1, ] D.(1,+∞)
3
6.牛顿冷却定律(Newton’s law of cooling)是牛顿在1701年用实验确定的:物体在空气中冷却,如果物体
的初始温度为θ ºC,环境温度为θ ºC,则t分钟后物体的温度θ(单位:ºC)满足:θ=θ +(θ -θ )e-
1 0 0 1 0
kt.已知环境温度为20 ºC,一块面包从温度为140 ºC的烤箱里拿出,经过10分钟温度降为80 ºC,那么
大约再经过( )分钟,温度降为35 ºC.
A.10 B.20 C.30 D.40
7.已知函数 f(x)是定义在 R 上的奇函数,且 f(x)在[0,+∞)上单调递减,f(2)=-1.若关于 x 的方程 f(x2+4x+t)=1在[1,3]上有解,则实数t的最大值为
A.23 B.7 C.-7 D.-23
8.若ex-2=e2y,则x-y的最小值为
(参考:a≥b>0lna≥lnb,ea≥eba≥b.)
2ln2 4ln2 3ln2 3ln2
A. B. C. D.
3 3 2 4
二、选择题:本大题共3 小题,每小题 6分,共 18 分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 已知a>b>c>0,下列不等式一定成立的是
a+b c c
A.b< <a B. <
2 a b
b c b b+a
C. > D. <
a-b b-c c c+a
10.设a,b,c为实数,已知关于x的不等式ax2+bx+c>0的解集为{x|1<x<3},下列说法中正确的是
A.a<0
B.4a-2b+c>0
1
C.关于x的不等式cx2+bx+a<0的解集为{x|x< 或x>1}
3
D.若关于x的不等式ax2+bx+c>a2-4恰有3个整数解,则a∈(-2,-1]
11.设集合M是实数集R的子集,如果t∈R满足:对任意a>0,都存在x∈M,使得
0<|x-t|<a,则称t为集合M的聚点,下列说法中正确的是
n+1
A.1是集合{x|x= ,n∈N*}的聚点
n
B.0不是集合{x∈Z|x≠0}的聚点
n2-1
C.1不是集合{x|x= ,n∈N*}的聚点
n2+1
n
D.0是集合{x|x= ,n∈N*}的聚点
2n2+1
三、填空题:本大题共 3 小题,每小题 5分,共 15分.
12.已知二次函数f(x)满足f(x-1)=x2+x+2,则f(2)=___▲_____.
13.已知x>0,y>0,且x+y=1,若4x+1≥mxy恒成立,则实数m的最大值为___▲_____.
x f(x )-x f(x )
2 1 1 2
14.已知函数f(x)是定义在R上的奇函数,若对任意的x ,x ∈(0,+∞),且x ≠x ,都有不等式
1 2 1 2 x -x
1 2
>0,且f(-3)=-3,则不等式f(x-1)+1≥x的解集是___▲_____.
四、解答题:本大题共 5 小题,共 77分.请在答题卡指定区域内作答,作答时应写出必要的
文字说明,证明过程或演算步骤.
15.(13分)
计算下列各式的值:(1)16×( 16 ) - 2 1 -4 2×8 1 4-(-2025)0;
25
(2)log 3·错误!16+5错误!;
4
4 27
(3)log +lg5·lg20+(lg2)2.
3 3
16.(15分)
已知集合A={x|2m-4<x<3m+2},B={x|2x2-7x+5≤0}.
(1)若m=3,求A∪B,A∩(∁ B);
R
(2)若A∩B=,求实数m的取值范围.
17.(15分)
ax+b
已知函数f(x)= 是定义在(-3,3)上的奇函数,且f(1)=1.
9-x2
(1)求实数a,b的值;
(2)判断函数f(x)在(-3,3)上的单调性,并用定义证明你的结论;
(3)若f(t2-1)+f(1-5t)<0,求实数t的取值范围.
18.(17分)
海洋潮汐(Ocean Tide)是沿海地区的一种自然现象,古代称白天的河海涌水为
“潮”,晚上的为“汐”,合称为“潮汐”.习惯上把海水在海面垂直方向的涨落称
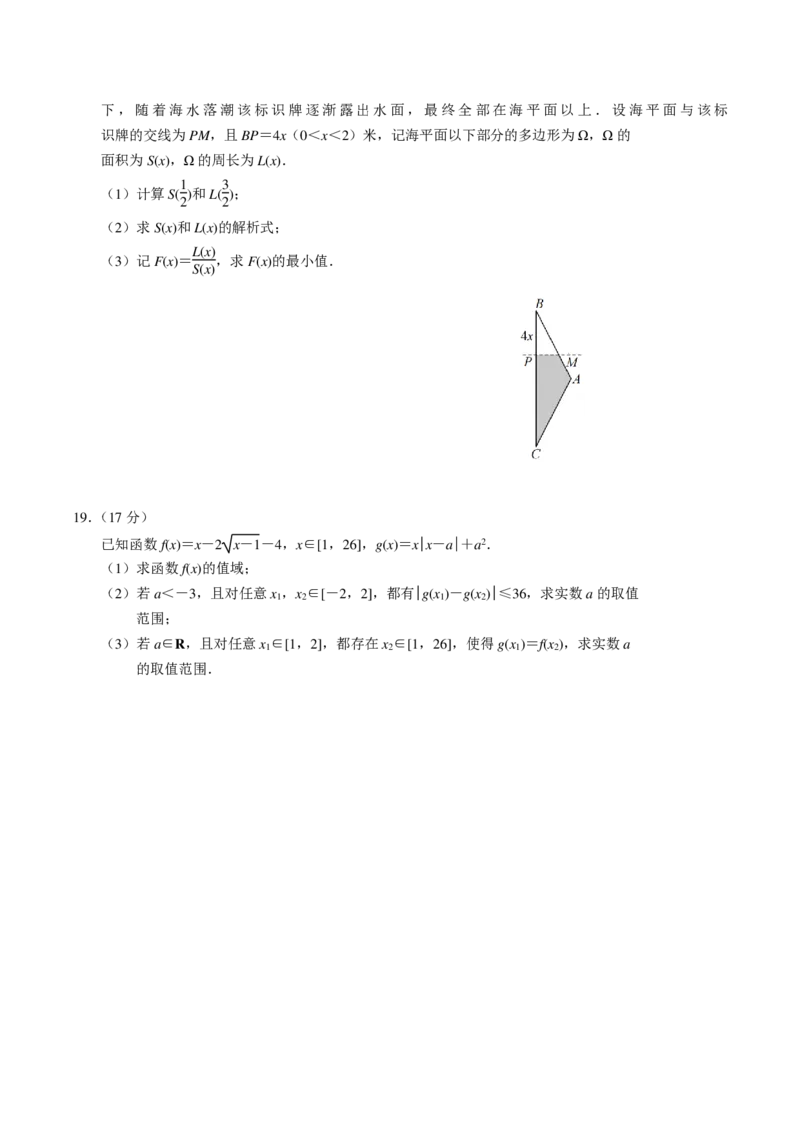
为潮汐,而海水在水平方向的流动称为潮流.如图所示,现在海里竖立着一块等腰三
角形状的标识牌,若该标识牌的腰长为 5 米,底边长为 8 米,开始时均在海平面以下,随着海水落潮该标识牌逐渐露出水面,最终全部在海平面以上.设海平面与该标
识牌的交线为PM,且BP=4x(0<x<2)米,记海平面以下部分的多边形为Ω,Ω的
面积为S(x),Ω的周长为L(x).
1 3
(1)计算S( )和L( );
2 2
(2)求S(x)和L(x)的解析式;
L(x)
(3)记F(x)= ,求F(x)的最小值.
S(x)
19.(17分)
已知函数f(x)=x-2 x-1-4,x∈[1,26],g(x)=x|x-a|+a2.
(1)求函数f(x)的值域;
(2)若a<-3,且对任意x ,x ∈[-2,2],都有|g(x )-g(x )|≤36,求实数a的取值
1 2 1 2
范围;
(3)若a∈R,且对任意x ∈[1,2],都存在x ∈[1,26],使得g(x )=f(x ),求实数a
1 2 1 2
的取值范围.一、选择题:本大题共 8 小题,每小题 5分,共 40 分.在每小题给出的四个选项中,只有一
项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.A 2.B 3.D 4.A 5.C 6.B 7.C 8.C
二.选择题:本题共 3小题,每小题 6分,共 18 分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,不选或有选错的得 0分.
9.AB 10.ACD 11.ABD
三、填空题:本大题共 3 小题,每小题 5分,共 15分.请把答案填写在答题卡相应位置上.
12.14 13.6+2 5 14.[-2,1]∪[4,+∞)
四、解答题:本大题共 6 小题,共 70分.请在答题卡指定区域内作答,解答时应写出必要的
文字说明,证明过程或演算步骤.
15.(13分)
16
解:(1)16×( )-4 2×8-(-2025)0
25
4 5
=16×( )-2×(23)-1=16× -2-1
5 4
=20-2-1=17. …………………………………………………………4分
(2)log
4
3·错误!16+5
=log
22
3·24+5·5=4log
2
3·log
3
2+5×6
=4+30=34. ………………………………………………………………………4分
4 27
(3)log +lg5·lg20+(lg2)2
3 3
=log +lg5·(lg2+1)+(lg2)2=log 3+lg5·lg2+(lg2)2+lg5
3 3
1 1
=- +lg2·(lg5+lg2)+lg5=- +lg2+lg5
4 4
1 3
=- +1= . ………………………………………………………………………5分
4 4
16.(15分)
解:(1)当m=1时,A={x|2<x<11}, …………………………………………………1分
5 7 5
B={x|x2+ ≤ x}={x|1≤x≤ }, …………………………………………………………2分
2 2 2
所以A∪B={x|1≤x<11}. …………………………………………………………………2分
5
又因为(∁ B)={x|x<1或x> },
R 2
5
所以A∩(∁ B)={x| <x<11}. ……………………………………………………………2分
R 25
(2)因为A∩B=,由于A={x|2m-4<x<3m+2},B={x|1≤x≤ },
2
①所以当A=时,则有2m-4≥3m+2,即m≤-6; …………………………………2分
m>-6
m>-6
②当A≠时,则有 或 5, ………………………………………3分
1≥3m+2 2m-4≥
2
1 13
解得-6<m≤- 或m≥ . ………………………………………………………………1分
3 4
1 13
综上所述,实数m的取值范围为(-∞,- ]∪[ ,+∞). ……………………………2分
3 4
17.(15分)
ax+b
解:(1)因为函数f(x)= 是定义在(-3,3)上的奇函数.
9-x2
b
所以f(0)= =0,解得b=0. .............................................1分
9
ax
则f(x)= .
9-x2
a
又因为f(1)=1,则 =1,解得a=8. ....................................1分
9-12
-8x 8x
经检验a=8,b=0时,f(-x)= =- =-f(x),
9-(-x)2 9-x2
8x
则f(x)= 是奇函数.
9-x2
所以a=8,b=0. .......................................................1分
8x
(2)因为f(x)= ,x∈(-3,3).
9-x2
函数f(x)在(-3,3)上单调递增, ..........................................1分
证明:任取-3<x <x <3. ..............................................1分
1 2
f(x )-f(x )=-
1 2
==
=(*) ..........................................1分
8(x -x )(x x +9)
1 2 1 2
= . .....................................1分
(3-x )(3+x )(3-x )(3+x )
1 1 2 2
【说明】如果只化到(*)式,扣1分,但不影响后续得分;若分子未因式分解到位,则证明过程除取值外
不给分.
因为-3<x <x <3,
1 2
所以3-x >0,3+x >0,3-x >0,3+x >0,x x +9>0,x -x <0,
1 1 2 2 1 2 1 2
8(x -x )(x x +9)
1 2 1 2
则f(x )-f(x )= <0,
1 2 (3-x )(3+x )(3-x )(3+x )
1 1 2 2所以f(x )-f(x )<0,即f(x )<f(x ),
1 2 1 2
故函数f(x)在(-3,3)上单调递增. .........................................2分
【说明】若未判断单调性,但正确证明单调递增,不扣分.
(3)函数f(x)是定义在(-3,3)上的奇函数,且f(t2-1)+f(1-5t)<0.
则f(t2-1)<-f(1-5t)=f(5t-1), ...........................................1分
因为函数f(x)在(-3,3)上单调递增.
-3<t2-1<3
所以-3<5t-1<3, ....................................................3分
t2-1<5t-1,
4 4
解得0<t< ,所以t的取值范围是(0, ). .................................2分
5 5
【说明】若未考虑定义域(即解得0<t<5)扣2分.
18.(17分)
1
解:(1)当x= 时,BP=2,
2
2 4 3
所以 = ,所以MP= .
MP 3 2
3
所以S = , ......................................................1分
△BPM 2
1 21
又因为S =12,所以S( )= . ......................................1分
△ABC 2 2
3
当x= 时,BP=6,所以CP=2
2
3 5
同理MP= ,又因为CM= ,
2 2
3
所以L( )=6. ........................................................1分
2
(2)①当0<4x≤4时,即0<x≤1时,
4x 4
因为 = ,所以MP=3x.
MP 3
1
所以S = ·3x·4x=6x2,
△BPM 2
又因为S =12,所以S(x)=12-6x2=-6x2+12. .......................2分
△ABC
L(x)=18-9x+3x=-6x+18. ..........................................1分
②当4<4x<8时,即1<x<2时,
因为CP=8-4x,
8-4x 4
所以 = ,所以MP=6-3x.
MP 31
所以S(x)= ·(6-3x)·(8-4x)=6x2-24x+24. .............................2分
2
L(x)=(6-3x)+(8-4x)+(10-5x)=-12x+24. ...........................1分
-6x2+12,0<x≤1
综上所述:S(x)= ,
6x2-24x+24,1<x<2
-6x+18,0<x≤1
L(x)= ...........................................1分
-12x+24,1<x<2.
(3)①当0<x≤1时,
L(x) -6x+18 x-3
F(x)= = = ,0<x≤1.
S(x) -6x2+12 x2-2
令t=x-3,则t∈(-3,-2],且x=t+3.
t t
所以y= = =错误!
(t+3)2-2 t2+6t+7
=错误!≥错误!=错误!=错误!. ...........3分
7
当且仅当-t=- ,即t=- 7,此时x=3- 7时取等号. .................1分
t
所以F(x) =F(3- 7)=错误!.
min
②当1<x<2时,
L(x) -12x+24 2
F(x)= = = ,1<x<2.
S(x) 6x2-24x+24 2-x
因为F(x)在[1,2)上单调递增,
所以F(x)>F(1)=2>错误!. ..........................................2分
综上所述,F(x)的最小值为错误!. ........................................1分
19.(17分)
解:(1)令t= x-1,t∈[0,5],则x=t2+1,
所以y=t2+1-2t-4=t2-2t-3,t∈[0,5]. ……………………………………………1分
因为对称轴t=1,所以f(x)∈[-4,12]. …………………………………………………2分
-x2+ax+a2,x≤a,
(2)因为g(x)=
x2-ax+a2,x>a.
由题意可知g(x) -g(x) ≤36.……………………………………………………………1分
max min
a
①若 ≤-2,即a≤-4时,
2
因为g(x)在[-2,2]上单调递增,
所以g(x) =g(2)=a2-2a+4,g(x) =g(-2)=a2+2a+4.
max min
所以g(x) -g(x) =-4a≤36,所以a≥-9.
max min
所以-9≤a≤-4.
a
②若 >-2,即-4<a<-3时,
2a a
因为g(x)在[-2, ]上单调递减,在[ ,2]上单调递增,且g(-2)<a2,g(2)>a2.
2 2
a 3
所以g(x) =g(2)=a2-2a+4,g(x) =g( )= a2.
max min 2 4
1
所以g(x) -g(x) = a2-2a+4≤36,即a2-8a-128≤0,所以-8≤a≤16.
max min 4
所以-4<a<-3.……………………………………………………………………………3分
【说明】一段正确给2分,两段均正确给3分.
综上所述a∈[-9,-3).……………………………………………………………………1分
(3)方法一:设y=g(x),x∈[1,2]的值域为集合A,f(x)的值域为集合B,所以AB.
由(1)知B=[-4,12].
①当a≤1时,
因为g(x)在[1,2]上单调递增,
所以g(x) =g(2)=a2-2a+4,g(x) =g(1)=a2-a+1.
max min
a2-a+1≥-4 a2-a+5≥0 a∈R
所以 ,即 ,即 ,解得-2≤a≤4.
a2-2a+4≤12 a2-2a-8≤0 -2≤a≤4
所以-2≤a≤1. ……………………………………………………………………………2分
a
②当 ≥2,即a≥4时,
2
因为g(x)在[1,2]上单调递增,
所以g(x) =g(2)=a2+2a-4,g(x) =g(1)=a2+a-1.
max min
a2+a-1≥-4 a2+a+3≥0
所以 ,即 ,即错误!,
a2+2a-4≤12 a2+2a-16≤0
解得-1- 17≤a≤-1+ 17.
所以无解. ……………………………………………………………………………………2分
1 a
③当1<a≤2时,则 < ≤1,
2 2
因为g(x)在[1,a]上单调递减,在[a,2]上单调递增,
所以g(x) =g(a)=a2,
min
又因为g(1)=a2+a-1,g(2)=a2-2a+4.
a2≥-4 a∈R
所以a2+a-1≤12 ,即a2+a-13≤0 ,即错误!,
a2-2a+4≤12 a2-2a-8≤0
解得-2≤a≤错误!.
所以1<a≤2.…………………………………………………………………………………2分
a
④当2<a<4时,则1< <2,
2a a
因为g(x)在[1, ]上单调递增,在[ ,2]上单调递减,
2 2
a 5a2
所以g(x) =g( )= ,
max 2 4
又因为g(1)=a2+a-1,g(2)=a2+2a-4.
所以错误!,即错误!,所以错误!,
4 15
所以2<a≤ .……………………………………………………………………………2分
5
4 15
综上所述-2≤a≤ . ……………………………………………………………………1分
5
方法二:设y=g(x),x∈[1,2]的值域为集合A,f(x)的值域为集合B,所以AB.
由(1)知B=[-4,12].
又因为当x∈[1,2]时,g(x)>0,所以只需g(x) ≤12.
max
①当a≤1时,
因为g(x)在[1,2]上单调递增,
所以g(x) =g(2)=a2-2a+4≤12.即a2-2a-8≤0,解得-2≤a≤4.
max
所以-2≤a≤1. ……………………………………………………………………………2分
a
②当 ≥2,即a≥4时,
2
因为g(x)在[1,2]上单调递增,
所以g(x) =g(2)=a2+2a-4≤12.即a2+2a-16≤0,解得-1- 17≤a≤-1+ 17.
max
所以无解. ……………………………………………………………………………………2分
1 a
③当1<a≤2时,则 < ≤1,
2 2
因为g(x)在[1,a]上单调递减,在[a,2]上单调递增,
又因为g(1)=a2+a-1,g(2)=a2-2a+4.
a2+a-1≤12 a2+a-13≤0
所以 ,即 ,即错误!,
a2-2a+4≤12 a2-2a-8≤0
解得-2≤a≤错误!.
所以1<a≤2.…………………………………………………………………………………2分
a
④当2<a<4时,则1< <2,
2
a a
因为g(x)在[1, ]上单调递增,在[ ,2]上单调递减,
2 2
a 5a2 4 15 4 15
所以g(x) =g( )= ≤12,解得- ≤a≤ .
max 2 4 5 5
4 15
所以2<a≤ .……………………………………………………………………………2分
5
4 15
综上所述-2≤a≤ . ……………………………………………………………………1分
5