文档内容
江苏省南京市2023-2024学年高一下学期6月期末考试数学试题
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1.(5分)若复数z满足(1+i)z=2,则z的虚部为( )
A.﹣1 B.﹣i C.i D.1
2.(5分)从分别写有1,2,3,4的4张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之和
是偶数的概率为( )
A. B. C. D.
3.(5分)设 是空间中的一个平面,l,m,n是三条不同的直线,则( )
A.若m ,αn ,l⊥m,l⊥n,则l⊥
B.若l∥⊂mα,m⊂∥αn,l⊥ ,则n⊥ α
C.若l∥m,m⊥ ,n⊥α ,则l⊥αn
D.若m ,n⊥α,l⊥nα,则l∥m
⊂α α
4.(5分)如图,在等边△ABC中,BC=4,点P为边BC上的一动点,则 的最小值为( )
A.0 B.﹣1 C.﹣2 D.
5.(5分)已知平面向量 =(1,3), =(1,﹣2),则 在 方向上的投影向量为( )
A.(1,﹣2) B.(﹣1,2) C.(﹣2,4) D.(3,﹣6)
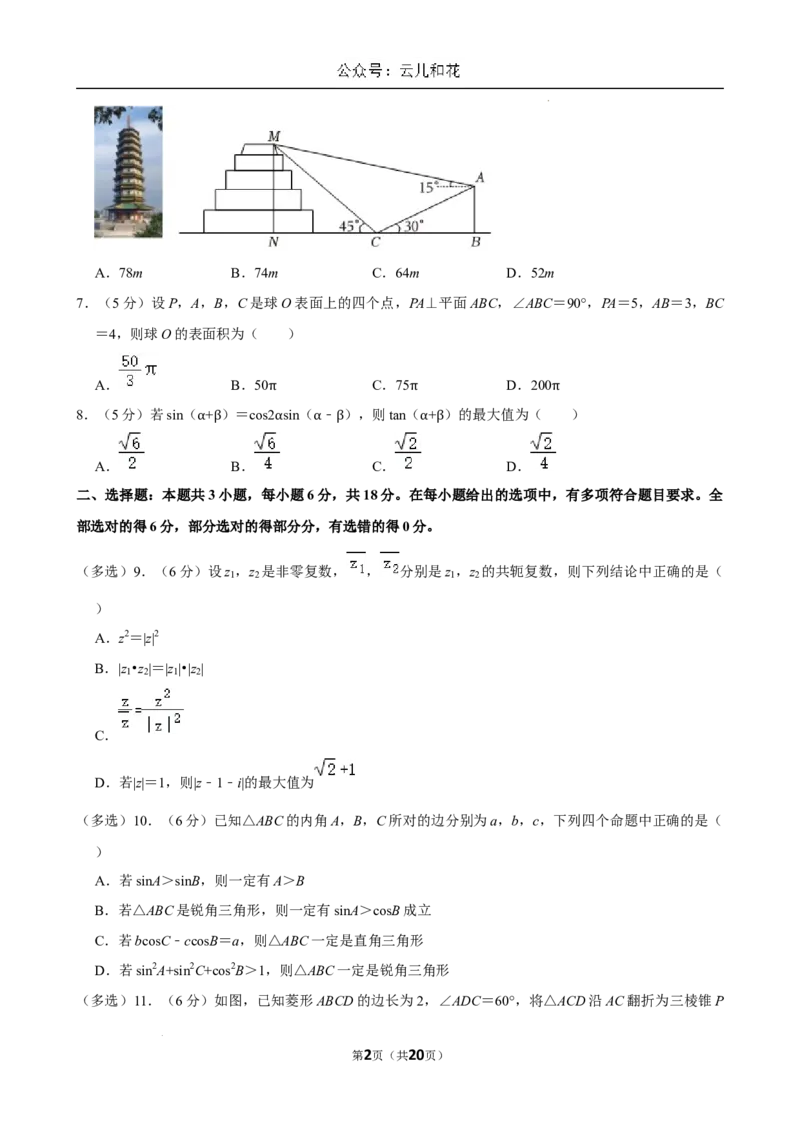
6.(5分)如图,某同学为测量南京大报恩寺琉璃塔的高度 MN,在琉璃塔的正东方向找到一座建筑物
AB,高约为39m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A和琉璃塔顶部M的仰角分
别为30°和45°,在A处测得塔顶部M的仰角为15°,则琉璃塔的高度约为( )
第1页(共20页)
学科网(北京)股份有限公司A.78m B.74m C.64m D.52m
7.(5分)设P,A,B,C是球O表面上的四个点,PA⊥平面ABC,∠ABC=90°,PA=5,AB=3,BC
=4,则球O的表面积为( )
A. B.50 C.75 D.200
8.(5分)若sin( + )=cos2π sin( ﹣ ),则tan(π + )的最大值为( π )
α β α α β α β
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全
部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)设z ,z 是非零复数, , 分别是z ,z 的共轭复数,则下列结论中正确的是(
1 2 1 2
)
A.z2=|z|2
B.|z •z |=|z |•|z |
1 2 1 2
C.
D.若|z|=1,则|z﹣1﹣i|的最大值为
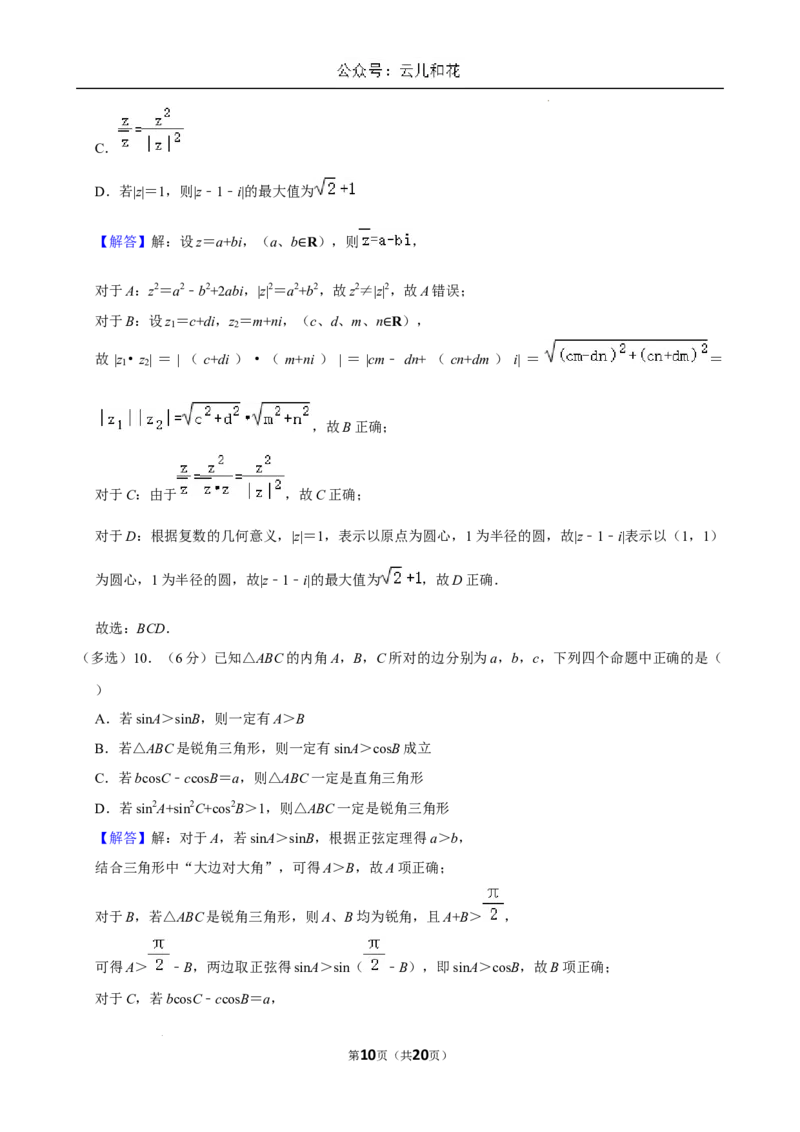
(多选)10.(6分)已知△ABC的内角A,B,C所对的边分别为a,b,c,下列四个命题中正确的是(
)
A.若sinA>sinB,则一定有A>B
B.若△ABC是锐角三角形,则一定有sinA>cosB成立
C.若bcosC﹣ccosB=a,则△ABC一定是直角三角形
D.若sin2A+sin2C+cos2B>1,则△ABC一定是锐角三角形
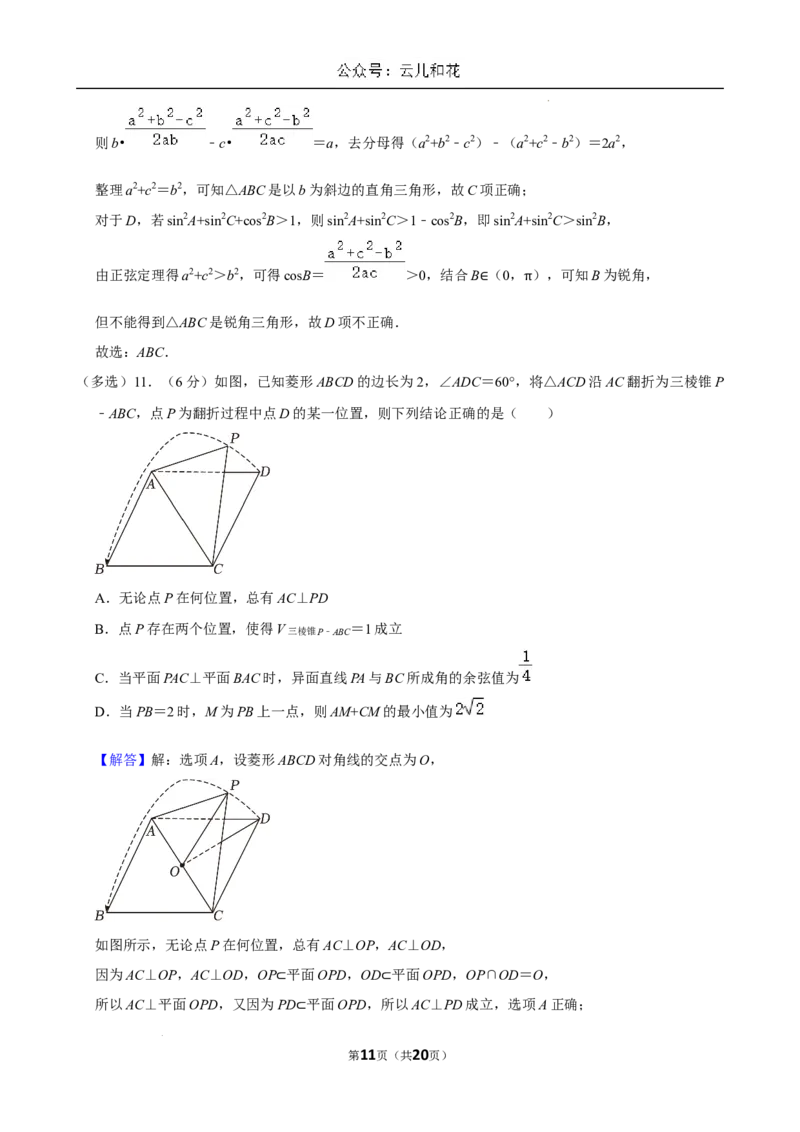
(多选)11.(6分)如图,已知菱形ABCD的边长为2,∠ADC=60°,将△ACD沿AC翻折为三棱锥P
第2页(共20页)
学科网(北京)股份有限公司﹣ABC,点P为翻折过程中点D的某一位置,则下列结论正确的是( )
A.无论点P在何位置,总有AC⊥PD
B.点P存在两个位置,使得V三棱锥P﹣ABC =1成立
C.当平面PAC⊥平面BAC时,异面直线PA与BC所成角的余弦值为
D.当PB=2时,M为PB上一点,则AM+CM的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)数据4,1,6,2,9,5,8的60百分位数为 .
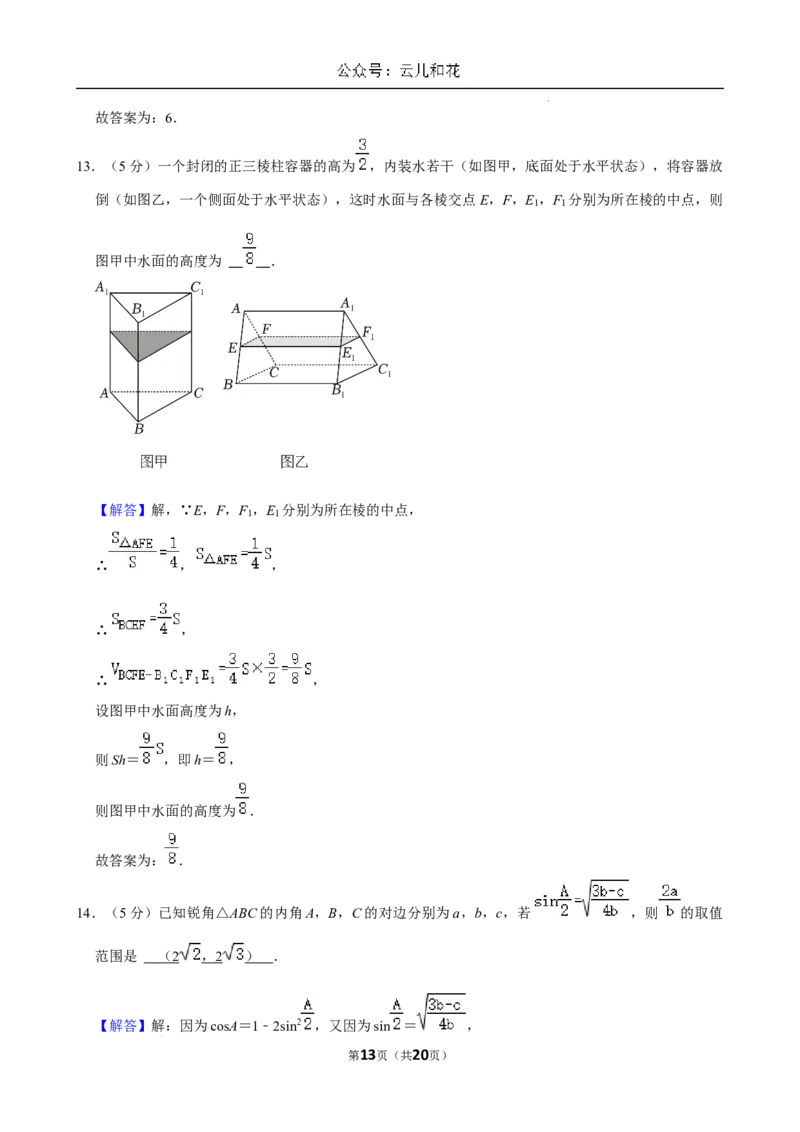
13.(5分)一个封闭的正三棱柱容器的高为 ,内装水若干(如图甲,底面处于水平状态),将容器放
倒(如图乙,一个侧面处于水平状态),这时水面与各棱交点 E,F,E ,F 分别为所在棱的中点,则
1 1
图甲中水面的高度为 .
14.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若 ,则 的取值
范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
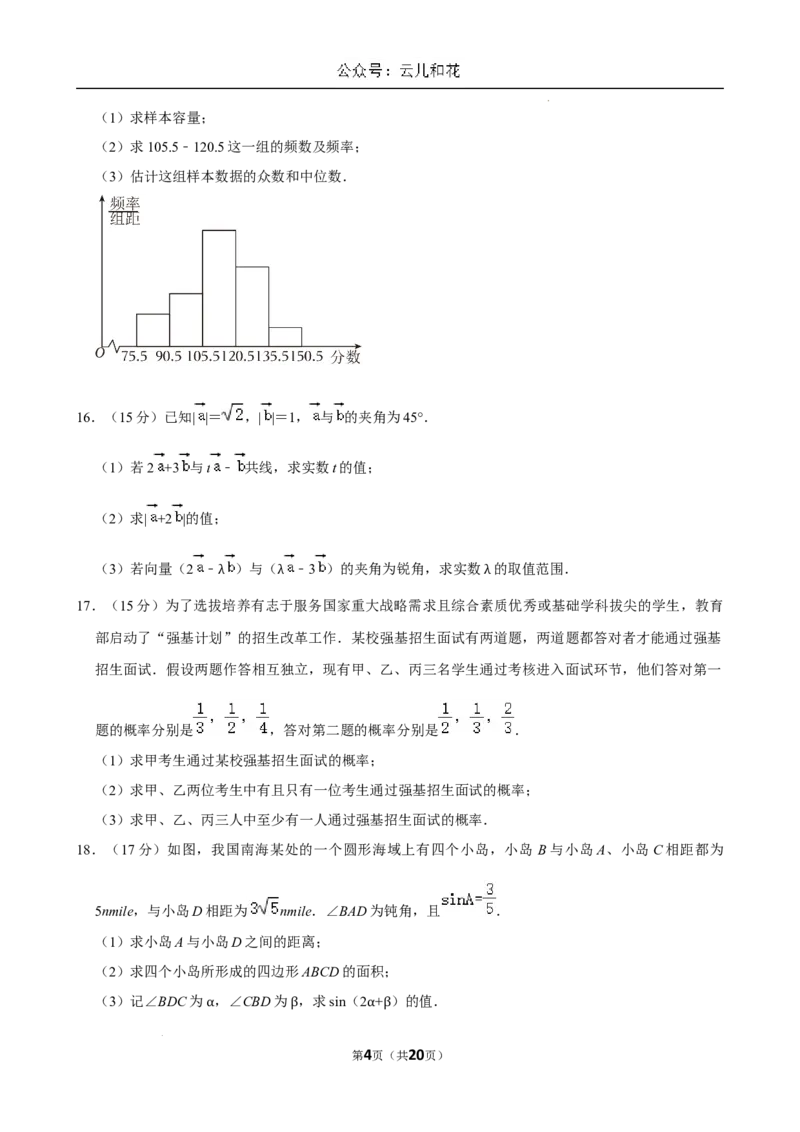
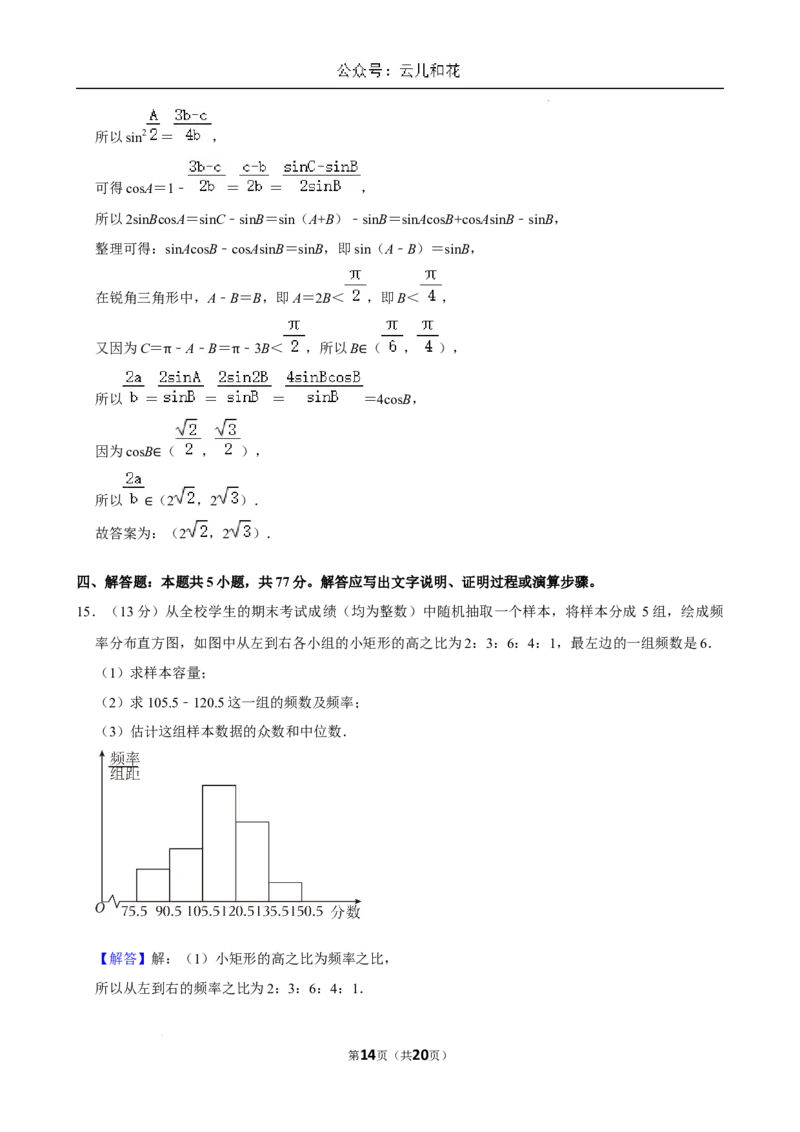
15.(13分)从全校学生的期末考试成绩(均为整数)中随机抽取一个样本,将样本分成 5组,绘成频
率分布直方图,如图中从左到右各小组的小矩形的高之比为2:3:6:4:1,最左边的一组频数是6.
第3页(共20页)
学科网(北京)股份有限公司(1)求样本容量;
(2)求105.5﹣120.5这一组的频数及频率;
(3)估计这组样本数据的众数和中位数.
16.(15分)已知| |= ,| |=1, 与 的夹角为45°.
(1)若2 +3 与t ﹣ 共线,求实数t的值;
(2)求| +2 |的值;
(3)若向量(2 ﹣ )与( ﹣3 )的夹角为锐角,求实数 的取值范围.
λ λ λ
17.(15分)为了选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生,教育
部启动了“强基计划”的招生改革工作.某校强基招生面试有两道题,两道题都答对者才能通过强基
招生面试.假设两题作答相互独立,现有甲、乙、丙三名学生通过考核进入面试环节,他们答对第一
题的概率分别是 ,答对第二题的概率分别是 .
(1)求甲考生通过某校强基招生面试的概率;
(2)求甲、乙两位考生中有且只有一位考生通过强基招生面试的概率;
(3)求甲、乙、丙三人中至少有一人通过强基招生面试的概率.
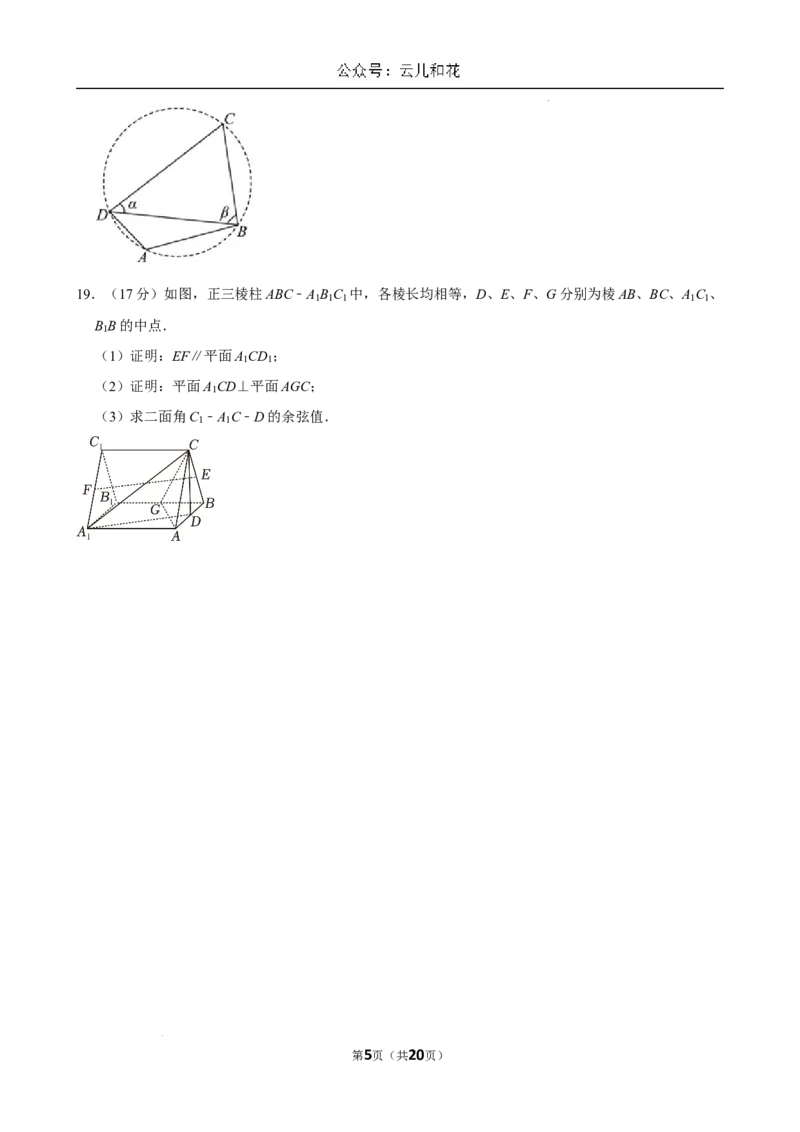
18.(17分)如图,我国南海某处的一个圆形海域上有四个小岛,小岛 B与小岛A、小岛C相距都为
5nmile,与小岛D相距为 nmile.∠BAD为钝角,且 .
(1)求小岛A与小岛D之间的距离;
(2)求四个小岛所形成的四边形ABCD的面积;
(3)记∠BDC为 ,∠CBD为 ,求sin(2 + )的值.
α β α β
第4页(共20页)
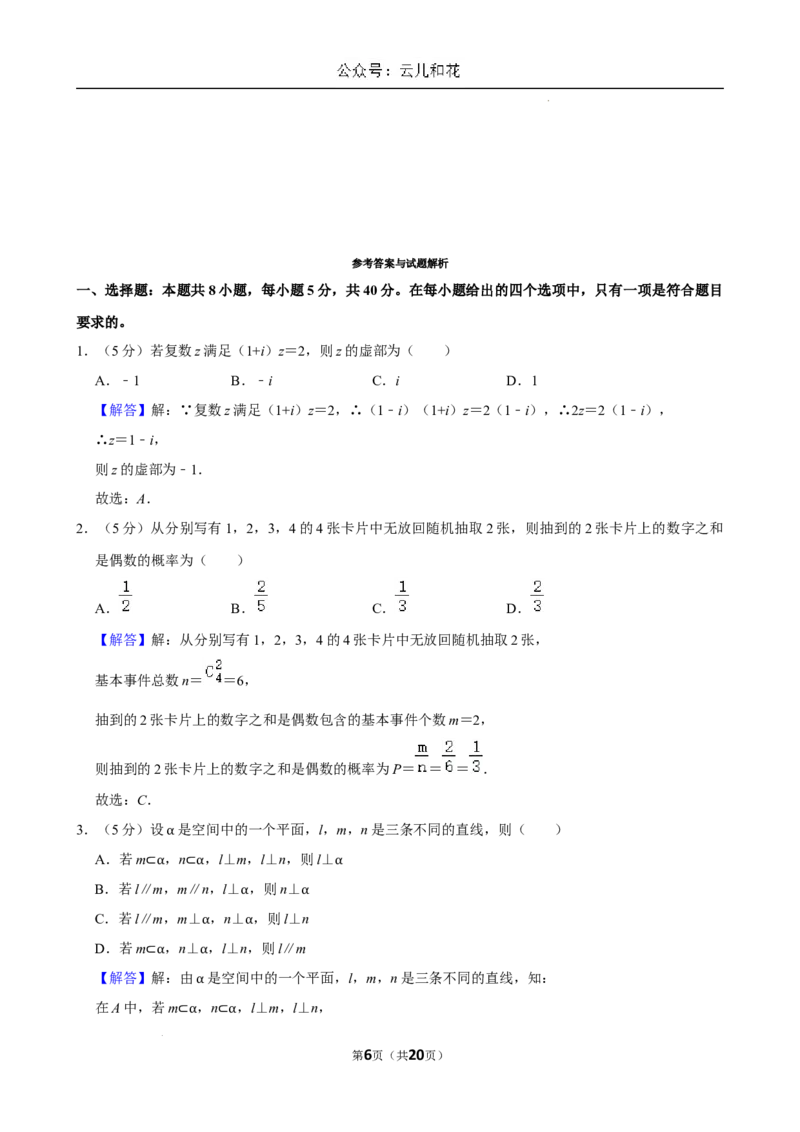
学科网(北京)股份有限公司19.(17分)如图,正三棱柱ABC﹣A B C 中,各棱长均相等,D、E、F、G分别为棱AB、BC、A C 、
1 1 1 1 1
B B的中点.
1
(1)证明:EF∥平面A CD ;
1 1
(2)证明:平面A CD⊥平面AGC;
1
(3)求二面角C ﹣A C﹣D的余弦值.
1 1
第5页(共20页)
学科网(北京)股份有限公司参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1.(5分)若复数z满足(1+i)z=2,则z的虚部为( )
A.﹣1 B.﹣i C.i D.1
【解答】解:∵复数z满足(1+i)z=2,∴(1﹣i)(1+i)z=2(1﹣i),∴2z=2(1﹣i),
∴z=1﹣i,
则z的虚部为﹣1.
故选:A.
2.(5分)从分别写有1,2,3,4的4张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之和
是偶数的概率为( )
A. B. C. D.
【解答】解:从分别写有1,2,3,4的4张卡片中无放回随机抽取2张,
基本事件总数n= =6,
抽到的2张卡片上的数字之和是偶数包含的基本事件个数m=2,
则抽到的2张卡片上的数字之和是偶数的概率为P= = = .
故选:C.
3.(5分)设 是空间中的一个平面,l,m,n是三条不同的直线,则( )
A.若m ,αn ,l⊥m,l⊥n,则l⊥
B.若l∥⊂mα,m⊂∥αn,l⊥ ,则n⊥ α
C.若l∥m,m⊥ ,n⊥α ,则l⊥αn
D.若m ,n⊥α,l⊥nα,则l∥m
【解答】⊂解α:由 α是空间中的一个平面,l,m,n是三条不同的直线,知:
在A中,若m α,n ,l⊥m,l⊥n,
⊂α ⊂α
第6页(共20页)
学科网(北京)股份有限公司则l与 相交、平行或l ,故A错误;
在B中α,若l∥m,m∥n⊂,αl⊥ ,
则由线面垂直的判定定理得nα⊥ ,故B正确;
在C中,若l∥m,m⊥ ,n⊥ ,α 则l∥n,故C错误;
在D中,若m ,n⊥α,l⊥nα,则l与m相交、平行或异面,故D错误.
故选:B. ⊂α α
4.(5分)如图,在等边△ABC中,BC=4,点P为边BC上的一动点,则 的最小值为( )
A.0 B.﹣1 C.﹣2 D.
【解答】解:由题意在等边△ABC中,BC=4,设 ,
则
=
= ,
当 时, 取到最小值﹣1,
故选:B.
5.(5分)已知平面向量 =(1,3), =(1,﹣2),则 在 方向上的投影向量为( )
A.(1,﹣2) B.(﹣1,2) C.(﹣2,4) D.(3,﹣6)
【解答】解: =(1,3), =(1,﹣2),
则 , ,
第7页(共20页)
学科网(北京)股份有限公司故则 在 方向上的投影向量为: = =(﹣1,2).
故选:B.
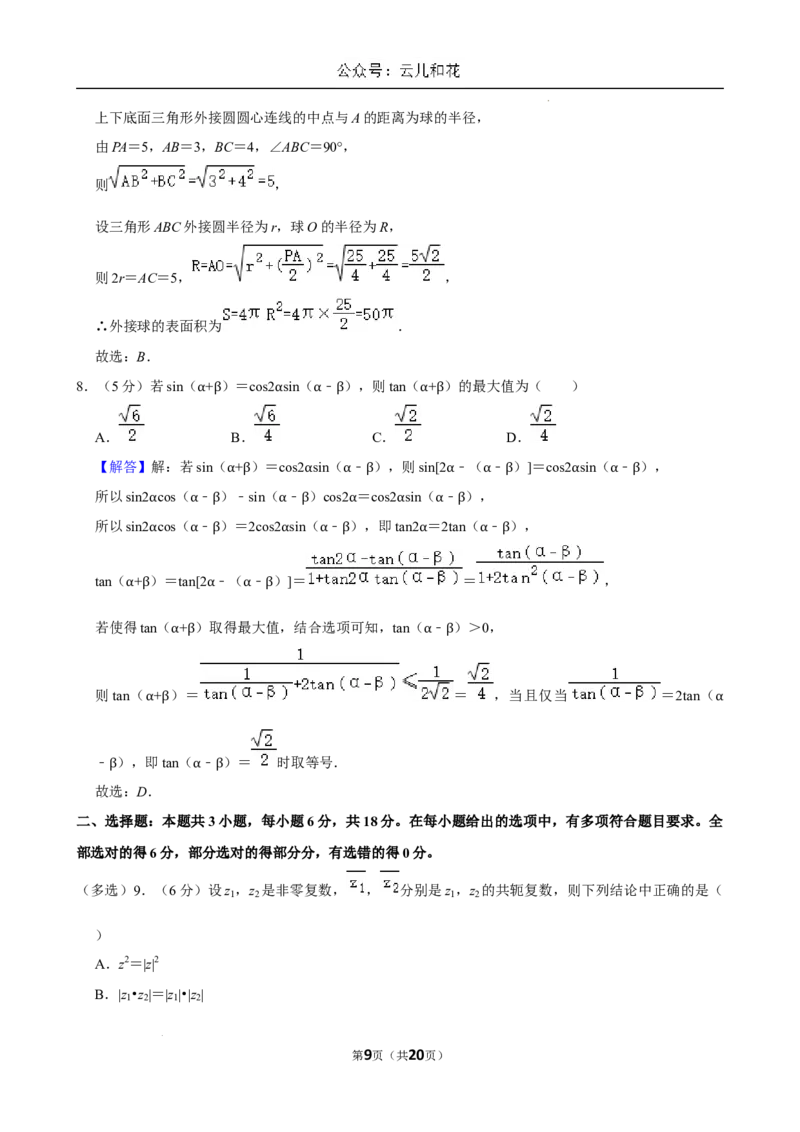
6.(5分)如图,某同学为测量南京大报恩寺琉璃塔的高度 MN,在琉璃塔的正东方向找到一座建筑物
AB,高约为39m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A和琉璃塔顶部M的仰角分
别为30°和45°,在A处测得塔顶部M的仰角为15°,则琉璃塔的高度约为( )
A.78m B.74m C.64m D.52m
【解答】解:根据题意,可得∠ACM=180°﹣45°﹣30°=105°,∠MAC=30°+15°=45°,
在△AMC中,∠AMC=180°﹣∠MAC﹣∠ACM=30°.
在Rt△ABC中,AB⊥AC,∠ACB=30°,所以AC=2AB=78m,
在△AMC中,由正弦定理得 = ,即 ,解得CM= ,
在Rt△MNC中,MN⊥CN,∠NCM=45°,所以MN=CMsin45°=78m.
故选:A.
7.(5分)设P,A,B,C是球O表面上的四个点,PA⊥平面ABC,∠ABC=90°,PA=5,AB=3,BC
=4,则球O的表面积为( )
A. B.50 C.75 D.200
【解答】解:由题意画出几何π体的图形如图, π π
把P、A、B、C扩展为三棱柱,
第8页(共20页)
学科网(北京)股份有限公司上下底面三角形外接圆圆心连线的中点与A的距离为球的半径,
由PA=5,AB=3,BC=4,∠ABC=90°,
则 ,
设三角形ABC外接圆半径为r,球O的半径为R,
则2r=AC=5, ,
∴外接球的表面积为 .
故选:B.
8.(5分)若sin( + )=cos2 sin( ﹣ ),则tan( + )的最大值为( )
α β α α β α β
A. B. C. D.
【解答】解:若sin( + )=cos2 sin( ﹣ ),则sin[2 ﹣( ﹣ )]=cos2 sin( ﹣ ),
所以sin2 cos( ﹣ )α﹣βsin( ﹣α)cos2α =βcos2 sin( ﹣α ),α β α α β
所以sin2αcos(α﹣β)=2cos2αsinβ( ﹣ α),即tαan2 =α2taβn( ﹣ ),
α α β α α β α α β
tan( + )=tan[2 ﹣( ﹣ )]= = ,
α β α α β
若使得tan( + )取得最大值,结合选项可知,tan( ﹣ )>0,
α β α β
则tan( + )= = ,当且仅当 =2tan(
α β α
﹣ ),即tan( ﹣ )= 时取等号.
故β选:D. α β
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全
部选对的得6分,部分选对的得部分分,有选错的得0分。
(多选)9.(6分)设z ,z 是非零复数, , 分别是z ,z 的共轭复数,则下列结论中正确的是(
1 2 1 2
)
A.z2=|z|2
B.|z •z |=|z |•|z |
1 2 1 2
第9页(共20页)
学科网(北京)股份有限公司C.
D.若|z|=1,则|z﹣1﹣i|的最大值为
【解答】解:设z=a+bi,(a、b R),则 ,
∈
对于A:z2=a2﹣b2+2abi,|z|2=a2+b2,故z2≠|z|2,故A错误;
对于B:设z =c+di,z =m+ni,(c、d、m、n R),
1 2
∈
故 |z • z | = | ( c+di ) • ( m+ni ) | = |cm﹣ dn+ ( cn+dm ) i| = =
1 2
,故B正确;
对于C:由于 ,故C正确;
对于D:根据复数的几何意义,|z|=1,表示以原点为圆心,1为半径的圆,故|z﹣1﹣i|表示以(1,1)
为圆心,1为半径的圆,故|z﹣1﹣i|的最大值为 ,故D正确.
故选:BCD.
(多选)10.(6分)已知△ABC的内角A,B,C所对的边分别为a,b,c,下列四个命题中正确的是(
)
A.若sinA>sinB,则一定有A>B
B.若△ABC是锐角三角形,则一定有sinA>cosB成立
C.若bcosC﹣ccosB=a,则△ABC一定是直角三角形
D.若sin2A+sin2C+cos2B>1,则△ABC一定是锐角三角形
【解答】解:对于A,若sinA>sinB,根据正弦定理得a>b,
结合三角形中“大边对大角”,可得A>B,故A项正确;
对于B,若△ABC是锐角三角形,则A、B均为锐角,且A+B> ,
可得A> ﹣B,两边取正弦得sinA>sin( ﹣B),即sinA>cosB,故B项正确;
对于C,若bcosC﹣ccosB=a,
第10页(共20页)
学科网(北京)股份有限公司则b• ﹣c• =a,去分母得(a2+b2﹣c2)﹣(a2+c2﹣b2)=2a2,
整理a2+c2=b2,可知△ABC是以b为斜边的直角三角形,故C项正确;
对于D,若sin2A+sin2C+cos2B>1,则sin2A+sin2C>1﹣cos2B,即sin2A+sin2C>sin2B,
由正弦定理得a2+c2>b2,可得cosB= >0,结合B (0, ),可知B为锐角,
∈ π
但不能得到△ABC是锐角三角形,故D项不正确.
故选:ABC.
(多选)11.(6分)如图,已知菱形ABCD的边长为2,∠ADC=60°,将△ACD沿AC翻折为三棱锥P
﹣ABC,点P为翻折过程中点D的某一位置,则下列结论正确的是( )
A.无论点P在何位置,总有AC⊥PD
B.点P存在两个位置,使得V三棱锥P﹣ABC =1成立
C.当平面PAC⊥平面BAC时,异面直线PA与BC所成角的余弦值为
D.当PB=2时,M为PB上一点,则AM+CM的最小值为
【解答】解:选项A,设菱形ABCD对角线的交点为O,
如图所示,无论点P在何位置,总有AC⊥OP,AC⊥OD,
因为AC⊥OP,AC⊥OD,OP 平面OPD,OD 平面OPD,OP∩OD=O,
所以AC⊥平面OPD,又因为⊂PD 平面OPD,所⊂以AC⊥PD成立,选项A正确;
⊂
第11页(共20页)
学科网(北京)股份有限公司选项B,点P旋转到使得平面APC⊥平面ADC成立时,V
P﹣ABC
取得最大值,
其中
使得V
P﹣ABC
=1成立,只有平面APC⊥平面ADC成立时的一个点,选项B错误;
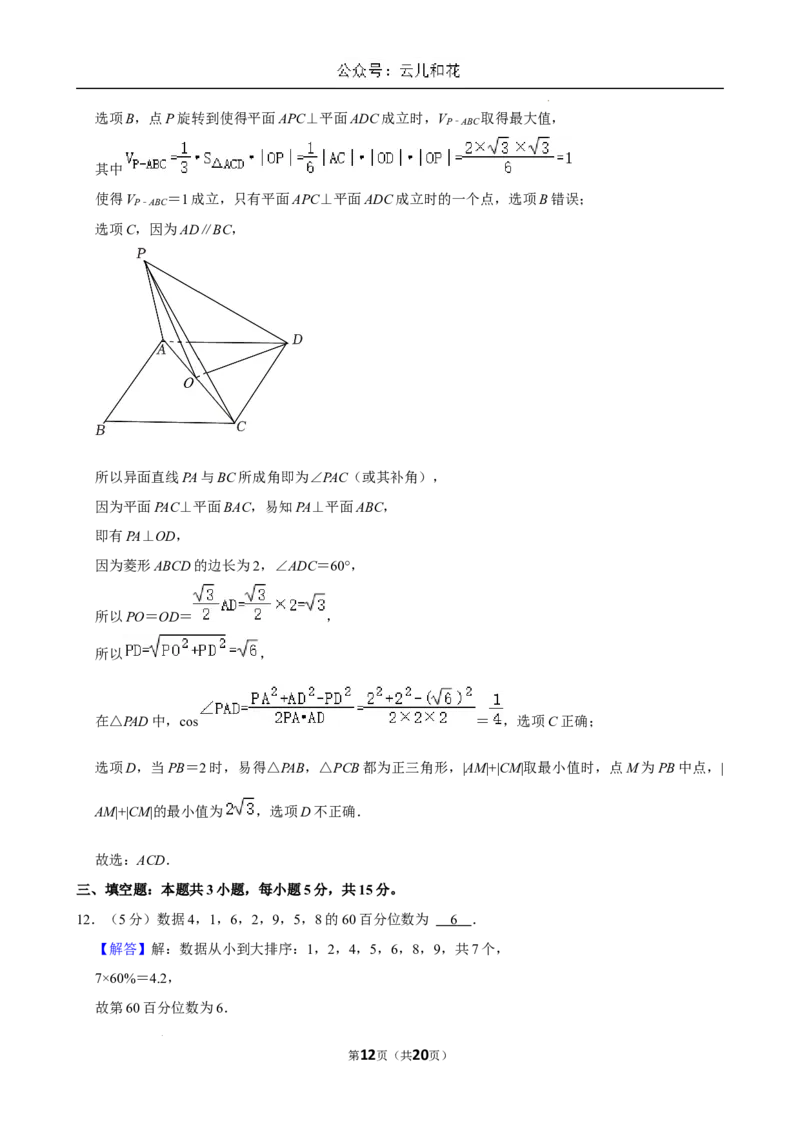
选项C,因为AD∥BC,
所以异面直线PA与BC所成角即为∠PAC(或其补角),
因为平面PAC⊥平面BAC,易知PA⊥平面ABC,
即有PA⊥OD,
因为菱形ABCD的边长为2,∠ADC=60°,
所以PO=OD= ,
所以 ,
在△PAD中,cos = ,选项C正确;
选项D,当PB=2时,易得△PAB,△PCB都为正三角形,|AM|+|CM|取最小值时,点M为PB中点,|
AM|+|CM|的最小值为 ,选项D不正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分。
12.(5分)数据4,1,6,2,9,5,8的60百分位数为 6 .
【解答】解:数据从小到大排序:1,2,4,5,6,8,9,共7个,
7×60%=4.2,
故第60百分位数为6.
第12页(共20页)
学科网(北京)股份有限公司故答案为:6.
13.(5分)一个封闭的正三棱柱容器的高为 ,内装水若干(如图甲,底面处于水平状态),将容器放
倒(如图乙,一个侧面处于水平状态),这时水面与各棱交点 E,F,E ,F 分别为所在棱的中点,则
1 1
图甲中水面的高度为 .
【解答】解,∵E,F,F ,E 分别为所在棱的中点,
1 1
∴ , ,
∴ ,
∴ ,
设图甲中水面高度为h,
则Sh= ,即h= ,
则图甲中水面的高度为 .
故答案为: .
14.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若 ,则 的取值
范围是 ( 2 , 2 ) .
【解答】解:因为cosA=1﹣2sin2 ,又因为sin = ,
第13页(共20页)
学科网(北京)股份有限公司所以sin2 = ,
可得cosA=1﹣ = = ,
所以2sinBcosA=sinC﹣sinB=sin(A+B)﹣sinB=sinAcosB+cosAsinB﹣sinB,
整理可得:sinAcosB﹣cosAsinB=sinB,即sin(A﹣B)=sinB,
在锐角三角形中,A﹣B=B,即A=2B< ,即B< ,
又因为C= ﹣A﹣B= ﹣3B< ,所以B ( , ),
π π ∈
所以 = = = =4cosB,
因为cosB ( , ),
∈
所以 (2 ,2 ).
故答案为∈:(2 ,2 ).
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)从全校学生的期末考试成绩(均为整数)中随机抽取一个样本,将样本分成 5组,绘成频
率分布直方图,如图中从左到右各小组的小矩形的高之比为2:3:6:4:1,最左边的一组频数是6.
(1)求样本容量;
(2)求105.5﹣120.5这一组的频数及频率;
(3)估计这组样本数据的众数和中位数.
【解答】解:(1)小矩形的高之比为频率之比,
所以从左到右的频率之比为2:3:6:4:1.
第14页(共20页)
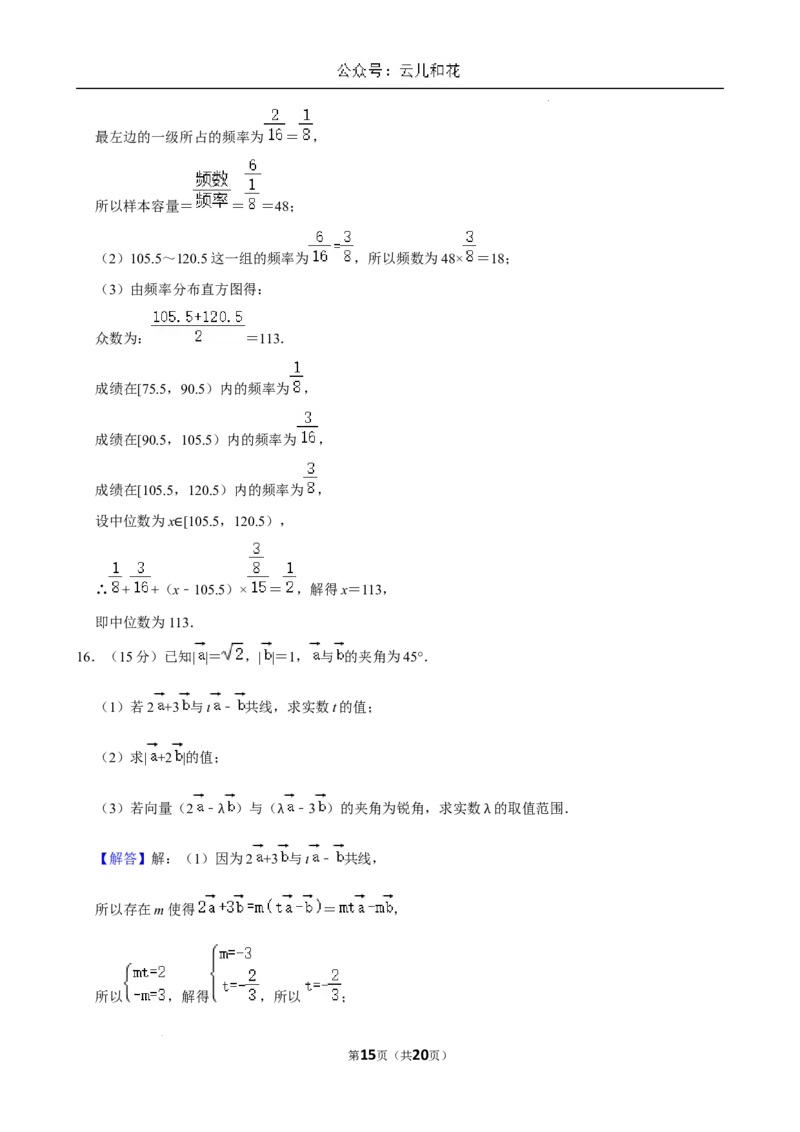
学科网(北京)股份有限公司最左边的一级所占的频率为 = ,
所以样本容量= = =48;
(2)105.5~120.5这一组的频率为 ,所以频数为48× =18;
(3)由频率分布直方图得:
众数为: =113.
成绩在[75.5,90.5)内的频率为 ,
成绩在[90.5,105.5)内的频率为 ,
成绩在[105.5,120.5)内的频率为 ,
设中位数为x [105.5,120.5),
∈
∴ + +(x﹣105.5)× = ,解得x=113,
即中位数为113.
16.(15分)已知| |= ,| |=1, 与 的夹角为45°.
(1)若2 +3 与t ﹣ 共线,求实数t的值;
(2)求| +2 |的值;
(3)若向量(2 ﹣ )与( ﹣3 )的夹角为锐角,求实数 的取值范围.
λ λ λ
【解答】解:(1)因为2 +3 与t ﹣ 共线,
所以存在m使得 = ,
所以 ,解得 ,所以 ;
第15页(共20页)
学科网(北京)股份有限公司(2)因为| |= ,| |=1, 与 的夹角为45°,
所以 • =| |•| |•cos45°= ×1× =1,
所以| +2 |2= 2+4 • +4 2=2+4+4=10,
则| +2 |= ;
(3)向量(2 ﹣ )与( ﹣3 )的夹角是锐角,
λ λ
可得(2 ﹣ )•( ﹣3 )>0,且(2 ﹣ )与( ﹣3 )不共线,
λ λ λ λ
即为2 2+3 2﹣(6+ 2) • >0,
λ λ λ
即有7 ﹣(6+ 2)>0,解得1< <6,
由(2λ﹣ )λ与( ﹣3 )共线λ,可得2•(﹣3)=﹣ • ,
λ λ λ λ
解得 =± ,
λ
则实数 的取值范围为(1, )∪( ,6).
λ
17.(15分)为了选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生,教育
部启动了“强基计划”的招生改革工作.某校强基招生面试有两道题,两道题都答对者才能通过强基
招生面试.假设两题作答相互独立,现有甲、乙、丙三名学生通过考核进入面试环节,他们答对第一
题的概率分别是 ,答对第二题的概率分别是 .
(1)求甲考生通过某校强基招生面试的概率;
(2)求甲、乙两位考生中有且只有一位考生通过强基招生面试的概率;
(3)求甲、乙、丙三人中至少有一人通过强基招生面试的概率.
【解答】解:(1)甲、乙、丙三名学生通过考核进入面试环节,
他们答对第一题的概率分别是 ,答对第二题的概率分别是 .
甲考生通过某校强基招生面试的概率为P = = .
1
第16页(共20页)
学科网(北京)股份有限公司(2)乙考生通过某校强基招生面试的概率为P = = ,
2
∴甲、乙两位考生中有且只有一位考生通过强基招生面试的概率为:
P= = .
(3)丙考生通过某校强基招生面试的概率为P = = ,
3
∴甲、乙、丙三人中至少有一人通过强基招生面试的概率为:
P′=1﹣(1﹣ )(1﹣ )(1﹣ )= .
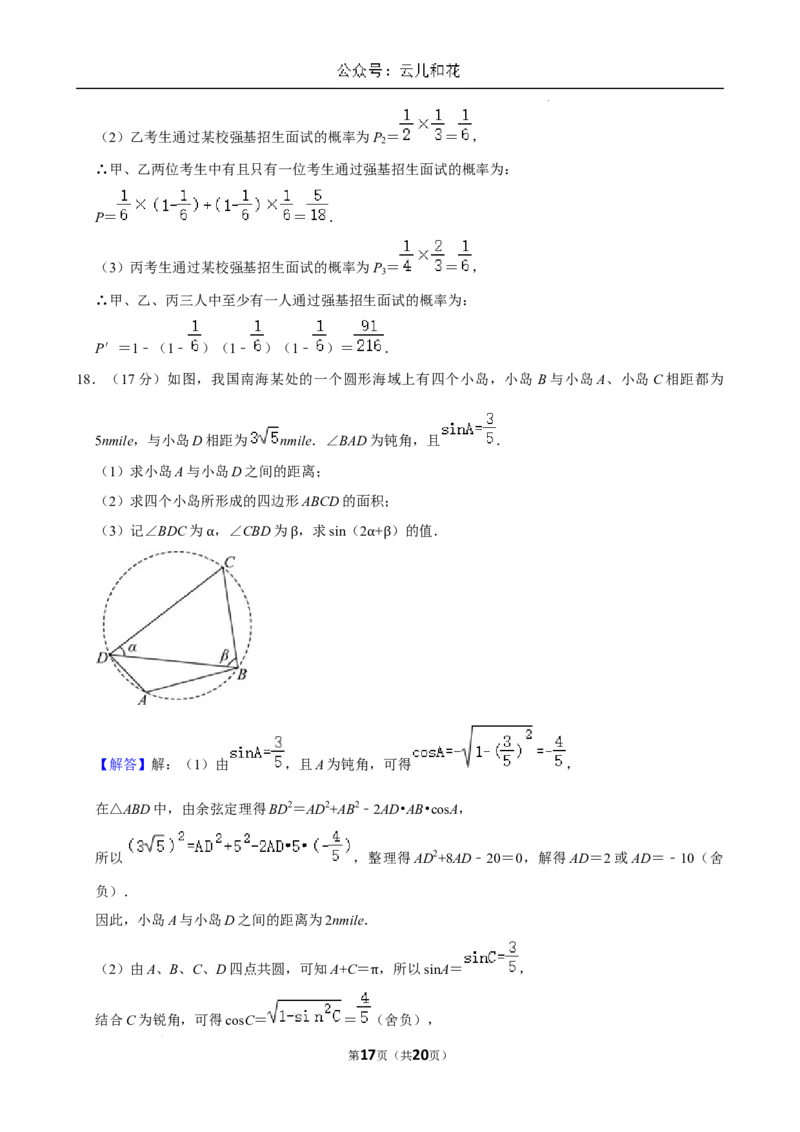
18.(17分)如图,我国南海某处的一个圆形海域上有四个小岛,小岛 B与小岛A、小岛C相距都为
5nmile,与小岛D相距为 nmile.∠BAD为钝角,且 .
(1)求小岛A与小岛D之间的距离;
(2)求四个小岛所形成的四边形ABCD的面积;
(3)记∠BDC为 ,∠CBD为 ,求sin(2 + )的值.
α β α β
【解答】解:(1)由 ,且A为钝角,可得 ,
在△ABD中,由余弦定理得BD2=AD2+AB2﹣2AD•AB•cosA,
所以 ,整理得AD2+8AD﹣20=0,解得AD=2或AD=﹣10(舍
负).
因此,小岛A与小岛D之间的距离为2nmile.
(2)由A、B、C、D四点共圆,可知A+C= ,所以sinA= ,
π
结合C为锐角,可得cosC= = (舍负),
第17页(共20页)
学科网(北京)股份有限公司在△BDC中,由余弦定理得CD2+CB2﹣2CD•CB•cosC=BD2,
即 ,整理得 CD2﹣8CD﹣20=0,解得 CD=10 或 CD=﹣2(舍
负).
因此,四边形ABCD的面积
= (平方海里),即四个小岛所形成的四边形的面积为18
平方海里.
(3)在△BDC中,由正弦定理得 ,即 ,解得 .
根据DC2+DB2>BC2,可得 为锐角,所以 (舍负),
α
因为 ,所以
,
因 此 , sin ( 2 + ) = sin[ + ( + ) ] = sin cos ( + ) +cos sin ( + ) =
α β α α β α α β α α β
.
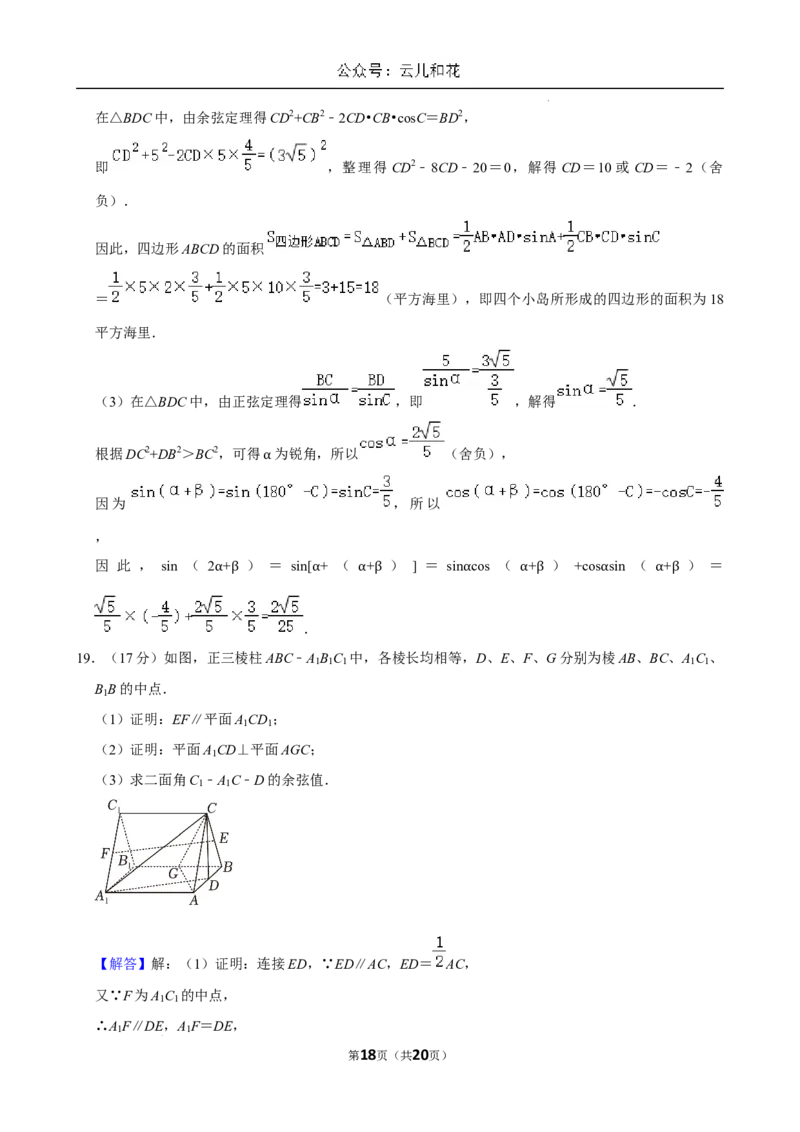
19.(17分)如图,正三棱柱ABC﹣A B C 中,各棱长均相等,D、E、F、G分别为棱AB、BC、A C 、
1 1 1 1 1
B B的中点.
1
(1)证明:EF∥平面A CD ;
1 1
(2)证明:平面A CD⊥平面AGC;
1
(3)求二面角C ﹣A C﹣D的余弦值.
1 1
【解答】解:(1)证明:连接ED,∵ED∥AC,ED= AC,
又∵F为A C 的中点,
1 1
∴A F∥DE,A F=DE,
1 1
第18页(共20页)
学科网(北京)股份有限公司∴四边形A DEF是平行四边形,
1
∴EF∥A D
1
又A D 平面A CD,EF 平面A CD,
1 1 1
∴EF∥⊂平面A 1 CD, ⊄
(2)证明:∵A A⊥平面ABC,
1
∴A A⊥CD,
1
∵D是AB的中点,
∴AB⊥CD
∴CD⊥平面A ABB ,
1 1
又因为GD 平面A ABB ,
1 1
∴CD⊥GD⊂,
在正方形ABB A 中,D、G分别为棱AB、B B的中点,
1 1 1
易知A D⊥AG,
1
∵A D∩CD=D,
1
∴AG⊥平面A DC,
1
又∵AG 平面AGC,
∴平面A⊂GC⊥平面A
1
DC.
(3)由(2)知CD⊥平面A ABB ,
1 1
∵CD 平面A CD,
1
∴平面⊂A
1
CD⊥平面平面A
1
ABB
1
,且平面A
1
CD∩平面A
1
ABB
1
=A
1
D,
∵A D⊥AG,设A D与AG交于点Q,则AQ⊥平面A CD,
1 1 1
过Q作QH垂直A C,连接AH,则AH⊥A C,
1 1
∴∠AHQ为二面角A﹣A C﹣D的平面角,
1
令A A=2a,则AD=a, ,
1
∴ ,
又因为A A=AC,AH⊥A C,
1 1
∴H为A C的中点,
1
∴ ,
第19页(共20页)
学科网(北京)股份有限公司在直角三角形AQH中, ,
由图易知,∠AHQ为锐角,
∴cos = ,
由图易知二面角C ﹣A C﹣D的平面角与二面角A﹣A C﹣D的平面角互补,
1 1 1
故二面角C ﹣A C﹣D的平面角的余弦值为 .
1 1
第20页(共20页)
学科网(北京)股份有限公司